一种新的单端行波测距方法

高效海，苏晓龙



一种新的单端行波测距方法

高效海1，苏晓龙2

(1.国网山东省电力公司经济技术研究院，山东 济南 250001；2.武汉供电公司，湖北 武汉 430000)

传统的单端行波测距方法存在远端故障测距不准确的问题。提出一种新的单端行波测距方案，其基本原理是故障点故障前电压与故障后初始行波电压相位差为，两者相关系数绝对值为1。通过测量点处故障前电压电流和故障后电压电流可以求出故障后初始行波和线路各点处的故障前电压。将各点处的故障前电压与所求初始行波进行相关性计算，得出相对应的相关系数的绝对值。在这些相关系数的绝对值中，数值最大且为1的点即为故障距离。与传统的行波测距方案相比，其测距具有单一值，远端故障也能准确测距。

行波测距；初始行波；故障前电压；相关系数

0 引言

传统的单端行波测距原理是利用行波传播的相关理论，通过初始行波和故障点反射波到达测量点的时间差与行波在线路上的传播速度，求得故障距离[1-5]。但当三相系统线路发生接地故障且故障点较远时，对端母线反射波会在故障点折射并领先到达测量点，导致对端母线反射波与故障点反射波混淆，使得测距结果不准确[6-10]。

针对传统单端行波测距所出现的问题，近几年研究的重点是如何识别第二个反射波的性质，进而提高测距的准确性[11-15]。但这些原理不仅存在各自的局限性，还使测距方案复杂。如文献[12]提出基于故障点反射波与初始正向行波波形一致的原理，采用相关法来识别故障点反射波与对端母线反射波。该方法原理可靠，但是在算法实现中如何选择合适的信号长度进行计算是一个难点，太长会导致拒动，太短又会导致误动。文献[13]通过相模变换，提取初始行波和第二个反射波的0模分量极性以及三个分别以A、B、C相为基准的1模分量极性。通过极性比较给出识别第二个反射波的极性。但是算法复杂，需要进行多次相模变换。

本文提出了一种新的单端行波测距的方法。其基本原理是利用故障点故障电压与故障后初始行波电压相位差为，两者相关系数的绝对值为1。根据测量点处故障前电压电流和故障后电压电流，求出初始行波和线路各点处故障前电压。通过相关法求出它们的相关系数，其绝对值最大的点所对应的距离，即为故障距离。与传统的单端行波测距方案相比，其测距值为单一值，不受对端母线的影响，故远端故障也能准确测距。

1 行波测距原理

1.1 两函数的相关系数

对于正弦量，由式(1)可知，当两个正弦函数相位相同，相关系数为1；当两个函数相位相差，相关系数为-1。而与正弦量的幅值无关。

1.2 故障点电压关系分析

电力线路系统如图1所示，线路长度为。

图1 线路系统图

Fig. 1Line system

发生故障时，对于故障系统，只考虑故障分量时，设故障点的初始行波为，其大小为

1.3 行波测距方案

根据上述分析，可以构成新的单端行波测距原理，具体阐述如下。

根据1.2节所述可知，只有故障点处的故障前电压与初始电压行波相关系数的绝对值为1。其他非故障点所求故障前电压与初始电压行波的相关性系数绝对值均小于1。且距故障距离越远，相关性系数绝对值越小。

综上所述，若故障发生于线路内部，在用上述步骤求得线路上所有点处的相关系数绝对值中，必然有一个极大值点，此点即接近故障点。若将线路上相邻的两点间隔缩小，即可精确测量故障距离，但计算机计算量也会随之增大。

测距方案如图2所示。

图2测距流程图

Fig. 2Flow chart of fault location

2 三相系统的处理

以上原理和方案都是以单相系统为例说明的。对于三相系统，此原理和方案同样适用，但要根据不同故障类型和相模变换，得到三相系统中相应的故障初始电压行波和线路各点处故障前电压。

对于利用克拉克变换，将耦合的三相线路解耦成独立的线模和零模分量的情况，根据文献[13]可知，三相系统中，不同故障类型对应的故障初始行波和线路各点处故障前电压如表1所示。

表1不同故障初始行波和线路故障前电压

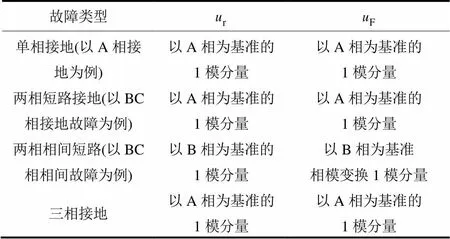
Table 1 Initial traveling wave and voltage before fault of different fault

其中，根据行波相关理论[13]，两相相间短路，以BC相相间故障为例，以A相为基准的相模变换，其1模分量为0，故选用以B相为基准的相模变换的1模变换。但相应与相位差为150°，所以在进行相关之前，要进行平移。这样才能保证相关系数最大点为故障点。

通过相模变换和初始行波、故障前电压的选择，即可以利用上述单相线路的故障测距方案进行距离测量。

3 仿真验证

为了验证以上分析结论的正确性，利用ATP软件进行仿真。仿真模型如图3所示。

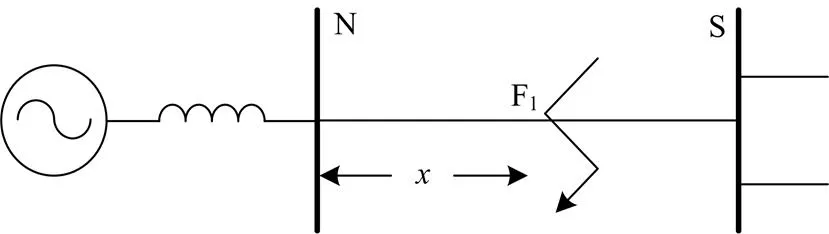
图3电力系统仿真图

Fig. 3Simulation of power system

系统电压等级为500 kV，输电线路采用均匀换位的分布参数模型。线路长度为300 km，正序、零序电阻分别为0.012 2 Ω/km和0.272 9 Ω/km，正序和零序电感分别为0.853 mH/km和2.673 9 mH/km，正序和零序电容分别为0.0136 7 μF/km和0.009 3 μF/km。

对于不同故障距离进行仿真。以线路发生A相接地故障为例，不同故障距离下的测距结果如表2所示。

表2A相接地故障时不同故障距离的测距结果

Table 2 Fault location result of different fault distance for phase A earth fault

其中故障位于100 km(近端故障)和200 km(远端故障)时，测距图如图4所示。

图4 距离与相关系数关系图

Fig. 4Relationship of correlation coefficients and distance

从上述仿真图可以看出，在线路各点处故障前电压与初始行波电压相关系数的绝对值中，故障点处有极大值。通过求得极大值点，即可求出对应的故障距离。

从仿真结果可以看出，对于不同的故障距离，本方案都能准确测距，误差均在理论误差范围内。

对线路不同故障进行仿真，当线路发生在100 km和200 km处的测距结果如表3所示。

表3 不同故障类型测距结果

从仿真结果可以看出，对于不同故障类型，本方案都能准确测距，误差均在理论误差范围内。

4 结论

本文提出了一种新的单端行波测距方案，该方案依据在线路的各点中，只有故障点初始行波和故障前电压的相关系数绝对值最大，通过求得初始行波和故障点故障前电压的相关系数绝对值最大点求出故障距离。由于本方案并不利用母线的反射波，所以不受对端母线的影响。对于远端故障，也能准确测距。

[1] 刘浩芳, 王增平, 徐岩, 等. 超高压输电线路波过程及暂态电流保护性能分析[J]. 电网技术, 2006, 30(3): 71-75.

LIU Haofang, WANG Zengping, XU Yan, et al. Analysis of transmission process of fault-generated travelling wave along EHV transmission lines and performance of transient current protection[J]. Power System Technology, 2006, 30(3): 71-75.

[2] 武骁, 何正友, 彭少博, 等. 基于行波固有频率的特高压直流输电线路纵联保护方法[J]. 电力系统保护与控制, 2013, 41(11): 67-73.

WU Xiao, HE Zhengyou, PENG Shaobo, et al. A UHVDC transmission line pilot protection method based on natural frequencies of traveling wave[J]. Power System Protection and Control, 2013, 41(11): 67-73.

[3] 何军娜, 陈剑云, 艾颖梅, 等. 电力系统行波测距方法及其发展[J]. 电力系统保护与控制, 2014, 42(24): 148-154.

HE Junna, CHEN Jianyun, AI Yingmei, et al. Fault location methods based on traveling wave theory for power system and its development[J]. Power System Protection and Control, 2014, 42(24): 148-154.

[4] 向强铭, 王茜, 陈靖秋, 等. 基于奇异值分解理论的双端行波故障测距的研究[J]. 电力系统保护与控制, 2014, 42(12): 14-18．

XIANG Qiangming, WANG Qian, CHEN Jingqiu, et al. Study of two-terminal traveling wave fault location based on SVD theory[J]. Power System Protection and Control, 2014, 42(12): 14-18．

[5] 秦小安．基于希尔伯特-黄变换的输电线路行波保护方法[D]. 长沙: 长沙理工大学, 2010．

[6] 位韶康, 陈平, 姜映辉. 一种不受波速影响的单端行波测距方法[J]. 电力系统保护与控制, 2013, 41(13): 76-81.

WEI Shaokang, CHEN Ping, JIANG Yinghui. A single- ended traveling wave ranging method avoiding wave speed influence[J]. Power System Protection and Control, 2013, 41(13): 76-81．

[7] 董杏丽, 葛耀中, 董新洲, 等．基于小波变换的行波测距式距离保护原理的研究[J]. 电网技术, 2001, 25(7): 9-13.

DONG Xingli, GE Yaozhong, DONG Xinzhou, et al. Wavelet transform based distance protection scheme with travelling wave fault location[J]. Power System Technology, 2001, 25(7): 9-13.

[8] 胥杰, 张永健, 孙嘉, 等. 基于模式识别的单端行波测距研究[J]. 高压电器, 2012, 48(6): 28-33.

XU Jie, ZHANG Yongjian, SUN Jia, et al. Single terminal travelling waves location based on pattern recognition[J]. High Voltage Apparatus, 2012, 48(6): 28-33.

[9] 施慎行, 董新洲, 周双喜. 单相接地故障行波分析[J].电力系统自动化, 2005, 29(23): 29-32.

SHI Shenxing, DONG Xinzhou, ZHOU Shuangxi. Analysis of single phase-to-ground fault generated traveling waves[J]. Automation of Electric Power Systems, 2005, 29(23): 29-32.

[10] 刘万超, 陈平, 孙佳佳, 等. 基于数学形态学的输电线路单端行波故障测距研究[J]. 电网与清洁能源, 2009, 25(4): 29-33.

LIU Wanchao, CHEN Ping, SUN Jiajia, et al. Fault locating of on single terminal traveling waves for transmission lines based on mathematical morphology and correlation function[J]. Power System and Clean Energy, 2009, 25(4): 29-33.

[11] 高效海, 何奔腾, 王慧芳, 等. 行波距离保护中识别第2个反射波性质的新方法[J]. 电网技术, 2013, 37(5): 1477-1482．

GAO Xiaohai, HE Benteng, WANG Huifang, et al. The new scheme to recognize the nature of the second reflection wave in travelling wave based distance protection[J]. Power System Technology, 2013, 37(5): 1477-1482.

[12] CROSSLEYP A, MCLAREN P G. Distance protection based on travelling waves[J]. IEEE Transaction on Power Apparatus and System, 1983, 102(9): 2971-2982.

[13] 高效海. 输电线路行波距离保护的研究[D]．杭州: 浙江大学, 2013．

[14] SHEHAB-ELDIN E H, MCLAREN P G. Travelling wave distance protection-problem areas and solutions[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 894-902.

[15] 施慎行, 董新洲, 周双喜. 单相接地故障下第2个反行波识别的新方法[J]. 电力系统自动化, 2006, 30(1): 41-44.

SHI Shenxing, DONG Xinzhou, ZHOU Shuangxi. New principle to identify the second reverse traveling wave generated by single-phase-to-ground fault[J]. Automation of Electric Power Systems, 2006, 30(1): 41-44.

[16] 胡广书. 数字信号处理—理论算法与实现[M]. 北京: 清华大学出版社, 1997.

(编辑 魏小丽)

A new method for single-ended traveling wave fault location

GAO Xiaohai1, SU Xiaolong2

(1. Economy and Technology Research Institute of State Grid Shandong Electric Power Company, Jinan 250001, China;2. Wuhan Power Supply Company, Wuhan 430000, China)

Conventional single-ended traveling wave fault location method exists inaccurate remote location problem. A new single-ended traveling wave solution is presented. The fundamental principle is that there exists phase difference between the fault point voltage before fault and the initial travelling wave voltage and the absolute value of the correlation coefficient between the two is 1. By measuring the pre-fault and after fault voltage and current the initial traveling wave and voltage of the transmission line can be obtained. Of all these absolute correlation coefficients, the one of the largest value is the distance of the fault point. Compared with the traditional traveling wave solutions, the new method can get the fault distance accurately even when the fault point is near the opposite bus bar.

traveling wave fault location; initial traveling wave; voltage before fault; correlation coefficient

10.7667/PSPC141566

2015-02-20

高效海(1987-)，男，硕士研究生，主要从事电力系统继电保护方面的研究；E-mail: gaoxiaohaiee@163.com

苏晓龙(1988-)，男，硕士研究生，主要从事电力系统继电保护方面的研究。