仿拓扑群中的一个结果
2016-10-13方连花图金基谢利红
方连花,图金基,谢利红
仿拓扑群中的一个结果
方连花1,图金基2,谢利红3
(1.泉州信息工程学院 公共基础部,福建 泉州 362000;2.江门职业技术学院 数学系,广东 江门 529000;3.五邑大学 数学与计算科学学院,广东 江门 529020)
设是一个-balanced且满足的仿拓扑群,那么对每一包含单位元的开邻域,上存在一个左不变的伪拟度量满足以下条件:1);2)是中闭的不变子群;3)中任意和满足.
仿拓扑群;-balanced仿拓扑群;拟度量
1 引言与预备知识
在拓扑群中有如下著名结论.
定理A[1]设是-balanced拓扑群,那么对包含单位元的任何开邻域,存在上连续左不变的伪度量使得以下条件成立:
本文主要目的是将定理A推广到仿拓扑群中. 首先假设抽象群上没有拓扑结构. 设是上的实值函数,且满足对任意的有. 考虑以下条件:
2 主要结果
为建立仿拓扑群的拟度量化定理需要如下引理.
引理1[2]设是仿拓扑群中包含单位元的开集列且满足对任意有成立,且,那么在上存在伪拟范数满足如下条件:
引理2与文献[3]的引理2.6类似.
定义:
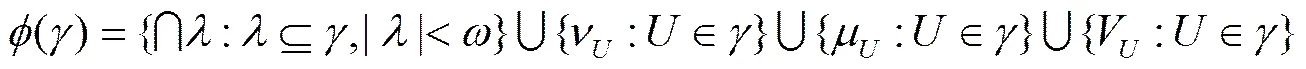
通过以上引理可以证明如下定理.

根据式(1)很容易得到.
这由引理2容易得到.
参考文献:
[1] ARHANGEL’SHII A, TKACHENKO M. Topological groups and related structures [M]. Paris: Atlantis Press, 2008.
[2] RAVSKY O V. Paratopological groups I [J]. Matematychni Studii, 2001, 16(1): 37-48.
[3] TKACHENKO M. Embedding paratopological groups into topological products [J]. Topology and its Applications, 2009, 156(7): 1298-1305.
[责任编辑:熊玉涛]
A Result of Paratopological Groups
FANGLian-hua1, TUJin-ji2, XIELi-hong3
(1.Department of Public-courses Teaching, Quanzhou Institute of Information Engineering, Quanzhou 362000, China; 2. Department of Mathematics, Jiangmen Polytechnic, Jiangmen 529000, China;3. School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)
In this paper, we mainly prove that: Letbe an-balanced paratopological group in which. Then, for every open neighbourhoodof the neutral elementin, there exists a left-invariant pseudoquasimetriconthat satisfies the following conditions: 1);2)is a closed invariant subgroup of; 3) for anyandin,.
paratopological groups;-balanced paratopological groups; quasimetric
1006-7302(2016)04-0005-04
O189.1
A
2016-04-12
国家自然科学基金青年基金资助项目(11601393);国家数学天元基金资助项目(11526158);广东省自然科学基金博士启动资助项目(2014A030310187);
方连花(1986—),女,福建泉州人,助教,硕士,研究方向为一般拓扑学、粗糙集.
