含机油油底壳的模态分析及实验验证

张之江，尹长城，杨文彪

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

含机油油底壳的模态分析及实验验证

张之江，尹长城，杨文彪

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

基于有限元法和实验模态分析2种方法计算含不同量机油时油底壳的固有频率和振型，实验结果验证了有限元模型的可靠性。结果表明：随着机油含量的增加，油底壳的频率逐渐降低，振型也发生了显著变化。

油底壳；流固耦合；有限元法；实验模态分析；频率

发动机油底壳是典型的薄壁型零件，极易产生诱导振动，其辐射噪声占整机总辐射噪声的20%左右［1］。在设计阶段对油底壳结构的动态特性进行准确的分析、预测和调整，对整机的减振降噪具有重要意义。本文中结合EQ4H型发动机油底壳，分别采用有限元和实验模态分析的方法，对含机油油底壳的动态特性进行分析，为后续油底壳的振动和噪声分析提供准确的条件。

1　基于有限元法模态分析

1.1虚拟质量法流固耦合模态分析

在海洋、船舶、航空和汽车等工程领域中，都会遇到流体和结构的相互作用问题，即流固耦合问题。按照耦合机理流固耦合问题可以分为2类问题：第1类是两相域部分或全部重叠在一起，很难明显地分开，如渗流问题；第2类是耦合作用仅发生在两相交界面上［2］。含油油底壳的模态分析属第2类问题。

虚拟质量法主要用来考虑水动力效应对结构响应的影响：液体会在湿表面产生附加质量，因此对结构振动有影响。虚拟质量并不是流体的实际质量，而是等效附加质量。此外，此方法不需要对流体区域划分网格，简化了前处理。

虚拟质量法的基本假设：1）流体无粘、无旋；2）流体不可压缩；3）同一流域具有统一的密度；4）有界流体必须具有流体自由面；5）自由面零压强假设；6）不考虑重力，晃荡、涡旋、湍流等；7）不考虑非线性效应、气弹效应。

虚拟质量法通过施加一个附加质量矩阵，实现不可压缩流体对结构的作用。流体中结构振动模态的有限元计算方程为

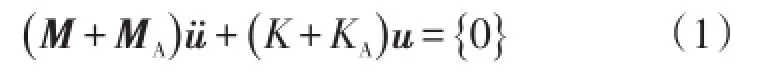
式中：M为结构质量矩阵；MA为流体作用对结构产生的附加质量矩阵；u，ü为位移和加速度向量。一般情况下，流体对结构的刚度KA相对结构本身的刚度小很多，因此可以忽略。从式（1）可以看出：附加质量矩阵随液体流动状态变化而变化，因此，结构的振动是液体流动状态的函数；另一方面，结构的振动以物面边界的形式对流体的流动产生影响，改变液体的运动状态。这时流体和结构之间就构成了一个封闭的动力学系统，这种流体和固体相互作用的问题是一个流固耦合问题。

根据流体力学的连续方程、运动方程、能量方程，求解Laplace方程可得速度势以及压力场：

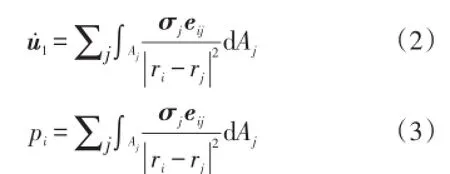
式中：u̇1为任意节点ri处速度向量；Aj为结构体表面上一微元的面积；σj为点 j处的流速向量；eij为从点 j到点i的单位向量。pi为任意面Aj上的压力；ρ为流体密度。

将式（2）～（3）积分，把压力转化为力，得到：

式中：F为节点压力；χ为速度方程（2）的积分矩阵；Λ为压力方程（3）的积分矩阵。

由牛顿第二定律：

将式（4）～（5）代入式（6）得到虚拟质量矩阵：

1.2基于Hypermesh和Optistruct有限元模态分析

采用Hypermesh进行有限元建模，采用Optis⁃truct 13.0进行虚拟质量法流固耦合计算。通过Mfluid卡片定义液体自由面高度和液体密度；Surf定义流固交界面；Param，Vmopt卡片指定流固耦合的算法即可完成求解设置。

有限元模型见图1。四面体单元数量为28 011，四边形单元数量为16 275，三角形单元数量为62。油底壳的弹性模量为210 GPa，泊松比为0.28，密度为7 900 kg·m-3，厚度为1.6 mm。分别对油底壳不含油、含油2.5 kg、含油5 kg、含油7.5 kg、含油10 kg 时5种情况进行自由模态分析，得到固有频率（表1），由表1可看出：油底壳每一阶的固有频率随着机油含量的增加而降低，说明机油对油底壳整体质量的影响大于对油底壳整体刚度的影响［4］。不含油和含油10 kg时油底壳的1阶、2阶振型见图2。

图1　有限元模型

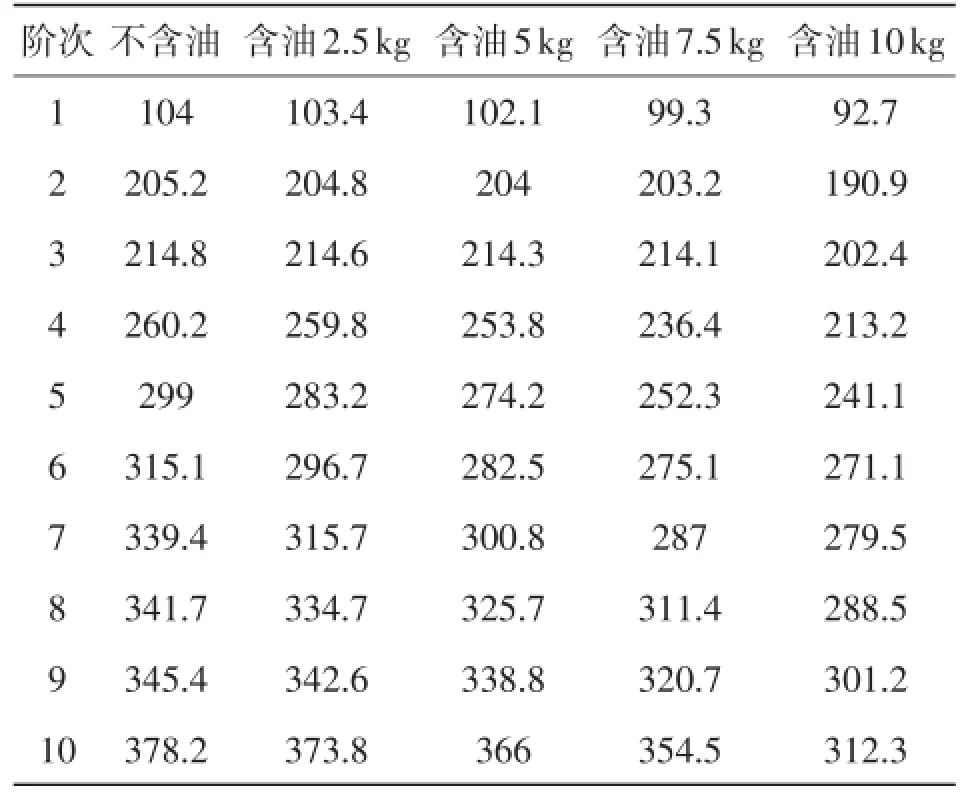
表1　有限元模态分析的固有频率　Hz

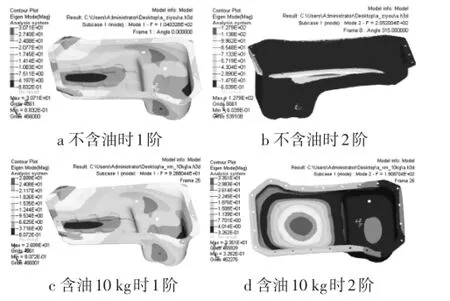
图2　油底壳有限元模态分析振型

2 基于BBM和LMS实验模态分析

实验模态分析又称模态分析的实验过程，是理论模态分析的逆过程。1）实验测得激励和响应的时间历程，运用数字信号处理技术求得频响函数（传递函数），得到系统的非参数模型；2）运用参数识别方法，求得系统模态参数；3）如果有必要，进一步确定系统的物理参数。因此，实验模态分析是综合运用现行振动理论、动态测试技术、数字信号处理和参数识别等手段，进行系统识别的过程［3］。本油底壳模态试验采用软橡皮绳悬挂，模拟油底壳的自由边界条件，如图3所示，沿油底壳的四周和底部均布58个测点。本实验采用力锤激励、BBMPAK系统进行数据采集，在每个激振点分别敲击5次，将5次的响应数据进行线性平均。采样频率设为1500 Hz（关心频率的2.56倍以上）。采用LMS软件进行模态参数识别，用PolyMax方法对测试数据进行处理，得到不含油、含油5 kg和含油10 kg时3种情况的固有频率如表2所示。不含油和含油10 kg时油底壳的1阶、2阶振型见图4。

图3　油底壳的自由悬吊

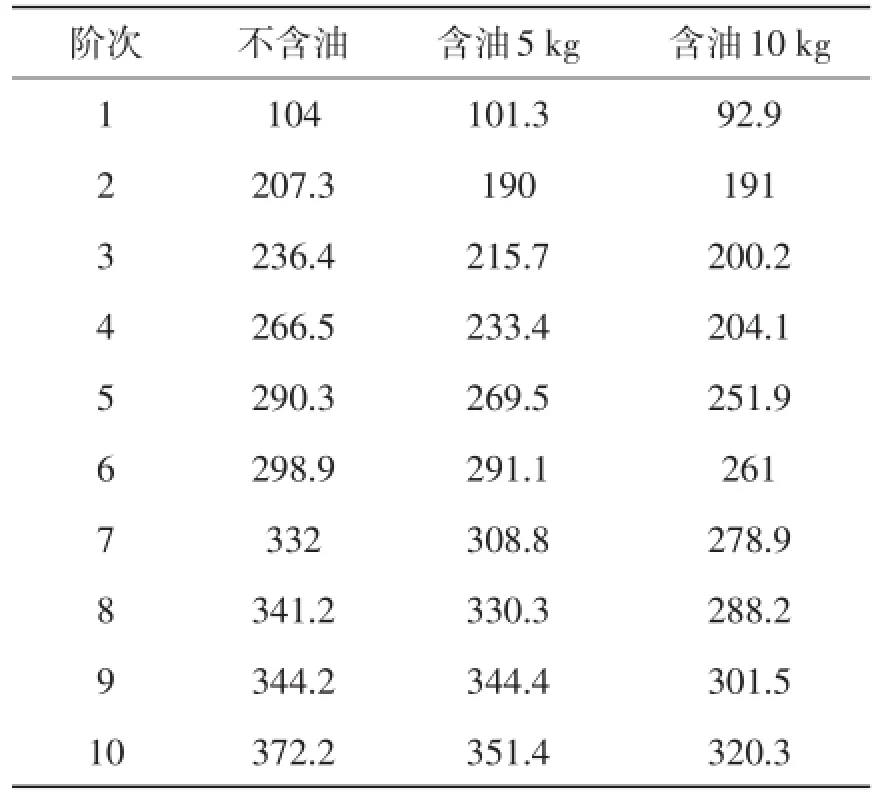
表2　实验模态分析的油底壳固有频率　Hz

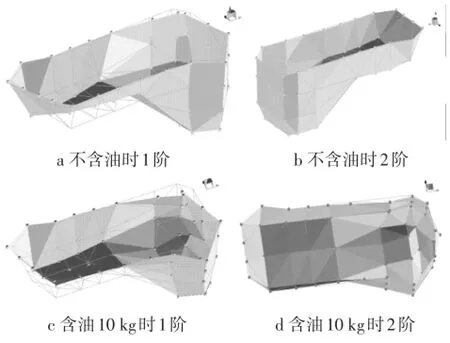
图4　油底壳实验模态分析振型

3　对比分析及结论

实验结果较好地验证了油底壳有限元模型的正确性，数值模态与实验模态存在一定的误差（表3），主要有以下原因：1）实验模态中的放油螺栓和传感器的附加质量影响；2）有限元模型存在离散误差和数值误差，而且不考虑阻尼的影响；3）实验过程存在噪声污染、泄露等测量误差［5］。

从图2和图4中可以看出，机油的存在对油底壳的振型也产生了影响：不含油时油底壳2阶振型为上表面长边振动，而含油10 kg时油底壳2阶振型变为下底部振动。因此，在实际工作中，考虑机油对油底壳的作用是很有必要的。

通过对含机油油底壳的自由模态分析，得到了准确的含机油油底壳的模态参数，可以在此基础上

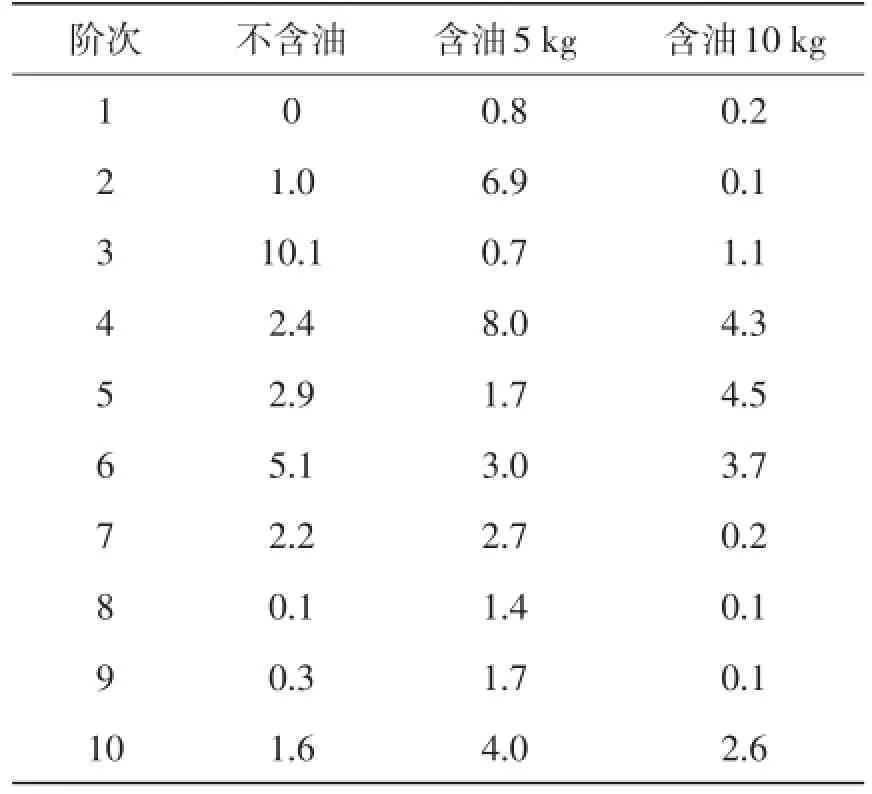
表3　有限元与实验模态分析的固有频率误差 %

进行准确的约束模态分析、形貌优化和瞬态响应分析等，有力于后续油底壳减振降噪的研究。

［1］庞剑，湛刚，何华.汽车噪声与振动——理论与应用［M］.北京：北京理工大学出版社，2006.

［2］王勖成.有限单元法［M］.北京：清华大学出版社，2003.

［3］曹树谦，张方德，萧龙翔.振动结构模态分析-理论、试验与应用［M］.天津：天津大学出版社，2001.

［4］沃德·海伦，斯蒂芬·拉门兹，波尔·萨斯.模态分析理论与试验［M］.白化同，郭继忠，译.北京：北京理工大学出版社，2001.

［5］尹长城，马迅，陈哲.基于ANSYS Workbench传动轴的模态分析［J］.湖北汽车工业学院学报，2013，27（1）：15-17+22.

［6］孙杰，绳锴，尹长城，张继伟.油底壳有限元模态分析及实验验证［J］.湖北汽车工业学院学报，2015，29（2）：13-15.

Modal Analysis and Experiment Verification of Oil Pan with Quantity of Lubricant

Zhang Zhijiang，Yin Changcheng，Yang Wenbiao
（School of Automotive Engineering，Hubei University of Automotive Technology，Shiyan 442002，China）

The inherent frequency and mode shapes of the oil pan with quantity of lubricant were calculat⁃ed by the finite element method and modalexperiment.The reliability of the finiteelementmodelswasver⁃ified by the experimental results.The Research results show that the modal frequencies of the oil pan de⁃crease gradually with the quantity of lubricant increasing，and the mode shapes also have significant changes.

oilpan；fluid-structureinteraction；FEM；experimental modal an alysis；frequency

U464；TK401

A

1008-5483（2016）02-0005-03

10.3969/j.issn.1008-5483.2016.02.002

2016-04-12

汽车动力传动与电子控制湖北省重点实验室开放基金项目（ZDK1201305）

张之江（1989-），男，湖北十堰人，硕士生，从事汽车有限元分析和振动方面的研究。E-mail：zhangzhijiang@163.com