一种基于塑性功和突变理论的边坡临界状态确定方法

李志平，彭振斌，何忠明，唐佳



一种基于塑性功和突变理论的边坡临界状态确定方法

李志平1, 2，彭振斌1，何忠明3，唐佳1

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 化工部长沙设计研究院，湖南长沙，410117；3. 长沙理工大学交通运输工程学院，湖南长沙，410114)

基于当前强度折减法的临界状态判据各有优缺点，结合塑性应变能理论和突变理论，提出一种新的反映边坡的临界状态失稳判据。该方法以塑性功作为评价边坡整体稳定性状态的评价指标，以尖点突变模型作为判断边坡失稳与否的理论依据。在具体操作过程中，通过不断调整强度折减系数，记录每个折减系系数下对应的计算模型整体塑性功，建立“整体塑性功−折减系数”曲线，并通过突变理论找出整体塑性功发生突变时对应的折减系数，此时的折减系数即为边坡的安全系数，此折减系数下对应的边坡状态即为临界状态。对单台阶边坡、多台阶边坡进行计算。研究结果表明：基于该方法得到的安全系数与极限平衡法得到的安全系数较接近，尤其与满足力平衡条件和力矩平衡条件的修正简布法所得结果最接近，从而验证了该方法的可靠性。

强度折减法；边坡稳定性；安全系数；临界状态判据；塑性应变能；突变理论

目前计算边坡安全系数的方法主要有2种：极限平衡法和强度折减法。与极限平衡法相比，强度折减法不需要事先假定滑动面的位置和形状，且考虑岩土体的本构模型等，因此，该方法在边坡稳定性分析中的应用越来越广泛[1−5]。但强度折减法在应用过程中需要面对的1个关键问题就是临界状态判据的选择，其对安全系数计算结果的影响至关重要。当前的临界状态判据主要分为3类[6−10]：1) 以塑性区的贯通为判据；2) 以数值计算的不收敛作为失稳判据；3) 以特征部位的位移突变性或加速度为零作为失稳判据。以上判据在一定程度上可以获得较合理的安全系数，对于较简单的边坡，安全系数较接近，但各自也存在一些缺陷：塑性区的贯通被认为是失稳的必要非充分条件，若以塑性区贯通作为判据，则有可能低估实际的安全系数；数值计算不收敛的原因并不是唯一的，有可能是达到临界状态失稳所致，也有可能是网格模型或计算程序本身存在缺陷所致，因此，得到的安全系数并一定可靠；通过局部点的特征点位移突变特征来搜寻临界状态面临的1个难题就是如何选择合适的特征点，特征点的选择不同，得到的安全系数通常也会出现差异。综上所述，当前的临界状态判据各有优缺点，但尚未形成统一的认识，因此，有必要继续对临界状态的判据进行探讨，进一步加深对临界状态判据的认识[11−14]。为此，本文作者结合塑性应变能理论和突变理论，提出一种新的反映边坡整体失稳过程的临界状态失稳判据，即不断调整强度折减系数，对每一步折减系数下的边坡进行弹塑性计算，计算完成后，对整个计算模型所有单元的塑性功进行累加，得到每个折减系系数下对应的计算模型整体的塑性功，建立“整体塑性功−折减系数”曲线，并通过突变理论找出整体塑性功发生突变时对应的折减系数，此时的折减系数即为边坡的安全系数，此折减系数下对应的边坡状态即为临界状态。最后，通过单台阶边坡、多台阶边坡验证该方法的可行性。

1 基本原理

1.1 塑性应变能的基本原理

基于弹塑性力学基本理论，当计算模型中某点的应力状态符合屈服准则后，应力状态点则沿着屈服面发生流动，某点的塑性应变能密度可表示为[15−16]

显然，W大于等于0，塑性应变能密度可以作为评价塑性状态的指标，塑性屈服越明显，则塑性应变越大，积累的塑性应变能亦越大。在一定范围内，对W进行积分即可得到整个区域塑性应变能：

对整个边坡而言，在确定的荷载条件下，随着强度参数降低，其屈服区域的面积从无到有并逐渐增大，即整个区域积累的塑性应变能逐渐增大；当边坡发生整体失稳时，其整体塑性应变能急剧增大。因此，整体塑性应变能可以从全局的角度反映边坡的渐进破坏过程。

在具体计算过程中，将坡体的抗剪切强度参数除以折减系数后得到新的强度参数，进而采用有限差分方法进行弹塑性计算。待计算完成后，遍历整个坡体的所有单元并判断单元的应力状态。若某单元处于塑性状态，则采用式(1)计算该单元的塑性应变能，将所有处于塑性状态单元的塑性应变能进行累加，则得到整个坡体的塑性应变能，由此可得到坡体塑性应变能与折减系数之间的曲线关系。

1.2 突变理论的基本原理

尖点突变模型是最实用、最简单的突变模型，已广泛应用于边坡稳定性评价、采矿顶板稳定性分析、地震液化评价、基坑支护评价等。尖点突变模型的势函数为[17−20]

式中：为状态变量；和为控制变量。由此可得到的表达式，令=0，可得平衡曲面方程为

此3次方程的实根判别式为

令=0即可得到分叉集方程。平衡曲面与分叉集的关系见图1[17]。由图1可知：平衡曲面在空间中的图形由上、中、下3叶构成，势函数对应的上、下叶的位置是稳定的，而对应的中间叶是不稳定的，因此，点只在上叶或下叶稳定地变化，一旦到达其边缘位置，便随即发生突变而跳过中叶。因此，系统状态的变化存在渐变和突变2种形式，当控制变量大于0时，系统状态位于奇点集的另一侧。状态变量的整个变化过程都是渐变的，当控制变量小于0时，系统状态位于奇点集的这一侧，状态变量在渐变过程中有可能从上叶直接突变到下叶。显然，当控制变量和处于分叉集内部即＜0时，系统处于不稳定状态；当控制变量和处于分叉集外部即＞0时，系统处于稳定平衡状态；当控制变量和满足分叉集方程即=0时，系统处于临界状态。

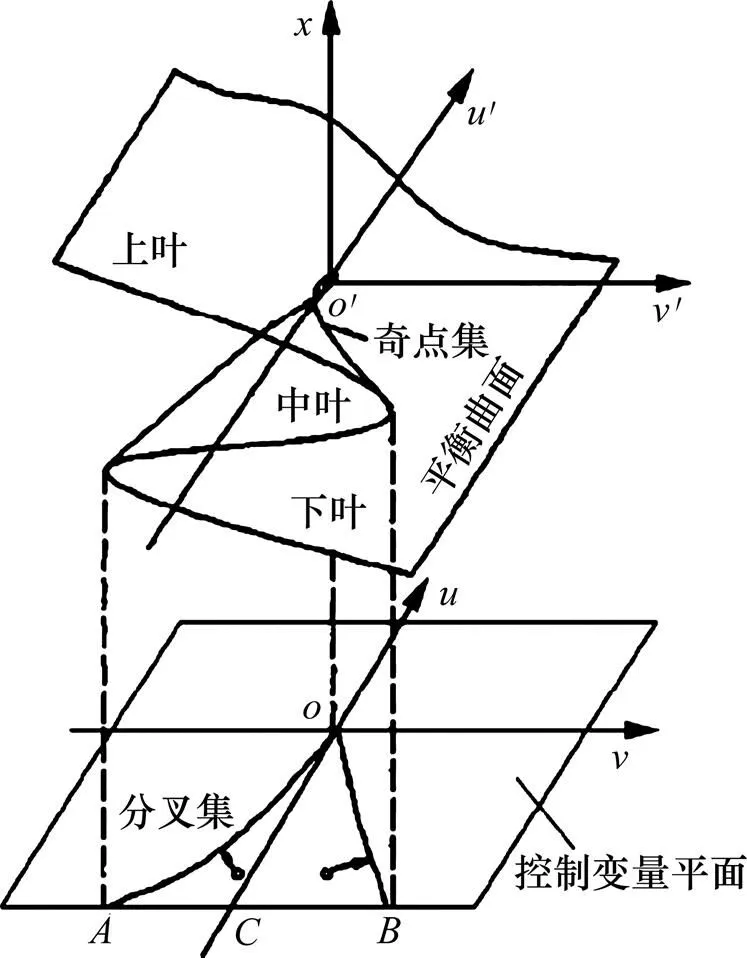
图1 尖点突变模型[17]

2 边坡失稳临界状态判别方法

边坡的失稳过程不是一蹴而就的，而是一个渐进破坏的过程，即坡体内部的屈服区域逐渐增大，当增大到一定程度时(临界状态)，边坡即发生滑动。采用强度折减法计算其安全系数时，不断增大强度参数的折减系数，根据折减系数更新强度参数后再进行弹塑性计算。随着折减系数的增大，坡体的强度参数逐渐降低，则每次弹塑性计算后坡体或坝体内部的塑性区面积是不断增大的，同时塑性应变也是逐渐增大的，若按照式(2)对整个坡体进行积分计算，则可得到其整体的塑性应变能。显然，随着折减系数的增大，整体塑性应变能也不断增大，当整体塑性应变能达到某个阀值(临界值)以后，坡体发生滑动，此后，塑性区面积和塑性应变增大更明显，因此，整体塑性应变能也显著增大。由此可见，整体塑性应变能可以反映坡体的渐进失稳过程，另外，塑性应变能可以表示为1个关于折减系数的函数。根据突变理论，塑性应变能可视为状态变量，用于表征坡体或坝体的发展状态，折减系数可视为控制变量，用于决定状态变量的取值。整体塑性应变能关于折减系数函数的泰勒展开式(截取至4次项)可表示如下：

式中：为整体塑性应变能，通过对坡体所有的塑性区域塑性应变能进行积分得到；为强度折减系数；0，1，2，3和4为待定系数。

式中：

对式(7)进行进一步变换，得到尖点突变的标准开折形式：

由此可得到尖点突变模型的判别式，根据判别式的取值情况即可判定坡体的状态。因此，根据突变理论确定临界状态的方法简述如下：首先根据强度折减法得到不同折减系数对应的坡体整体塑性应变能，通过多项式拟合技术便可得到塑性应变能与折减系数的函数关系式；然后，将关于的函数中的相关系数及不同的折减系数代入式(7)~(10)中，求得不同折减系数对应的和；将和代入判别式，即可得到不同折减系数下的，据可判定各个折减系数下坡体处于何种状态：＞0，表示在该折减系数下坡体尚处于稳定状态；＜0，表示该折减系数下坡体已发生滑动失稳；=0，表示在该折减系数下坡体恰好处于临界状态。可见此折减系数也为坡体的安全 系数。

3 算例分析

为了说明突变理论在确定坡体临界状态的可行性，下面通过算例阐述如何建立塑性应变能－折减系数的尖点突变模型，并基于该模型求解坡体的安全系数；同时，将强度折减法得到的安全系数与7种极限平衡法得到的安全系数进行对比研究，探讨本文方法计算安全系数的可靠性。需要说明的是，随着台阶数的增加，坡体既可能沿着某一级台阶发生局部垮塌，也可能发生整体失稳，因此，为了说明本文方法的适用性，采用4种不同台阶数的边坡进行稳定性分析。另外，为了提高数值计算的效率和精度，岩土体采用非关联流动法则，边坡模型采用四边形单元。

3.1 单台阶边坡算例

为了验证该方法的可靠性，选取澳大利亚计算机应用协会(ACADS)的边坡考题作为研究对象。该考题的边坡安全系数已被广泛认同，可作为验证其他方法计算边坡安全系数的基准。该考题为均质单台阶边坡，模型尺寸如图2所示，材料重度为20.0 kN/m3，弹性模量为10 MPa，泊松比为0.25，摩擦角为19.6°，黏结力为3.0 kPa[21]。

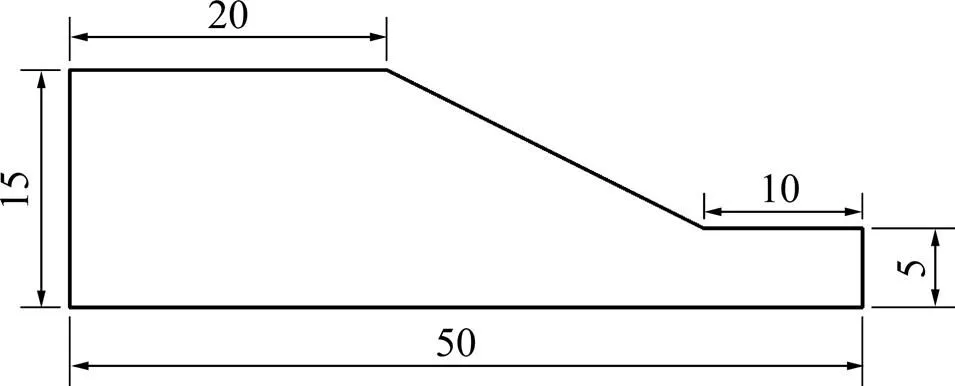
尺寸单位：m

通过不断调整强度折减系数，可得到坡体整体塑性应变能随折减系数的变化曲线，见图3。由图3可知塑性应变能的增长趋势明显分为2段：折减系数大约在1.00之前，塑性应变能增长缓慢；在此之后，塑性应变能急剧增大，表明坡体已失稳破坏，发生了塑性流动。为了确定使坡体恰好达到临界状态的折减系数，基于式(6)拟合得到各级折减系数下塑性应变能关于折减系数的函数关系式，并通过变换得到尖点突变模型的标准开折式，通过式(10)求解标准开折式的控制变量和，进而得到各级折减系数下的塑性应变能突变的判别值。塑性应变能判别值随折减系数的变化曲线见图4。图4中曲线与横轴的交点取值=0.998，此时=0，表明坡体恰好处于临界状态，因此，单台阶坡体计算模型的安全系数为0.998。由图4可知：当折减系数小于等于0.998时，均大于0，表明坡体尚处于稳定状态；当折减系数大于等于0.998时，均小于0，表明坡体已处于失稳状态。采用7种极限平衡法对此单台阶坡体进行稳定性分析，各种方法对应的安全系数见表1。从表1可知：本文所提方法的计算结果与各种极限平衡法的计算结果较接近，其中与满足严格极限平衡条件的修正简布法计算结果最接近。需要说明的是：本文的算例均采用圆弧滑面进行极限平衡计算。相关研究成果表明[22]，对于均质边坡而言，边坡的滑动面近似圆弧，采用圆弧滑动面进行边坡稳定性分析可以得到理想的结果。

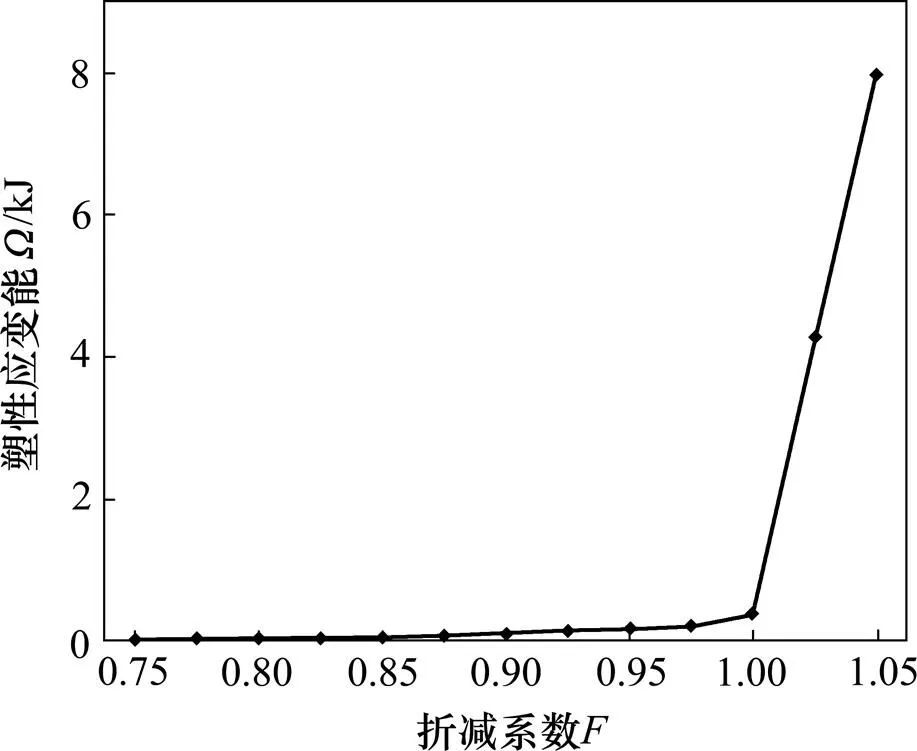
图3 单台阶坡体Ω与F的变化关系

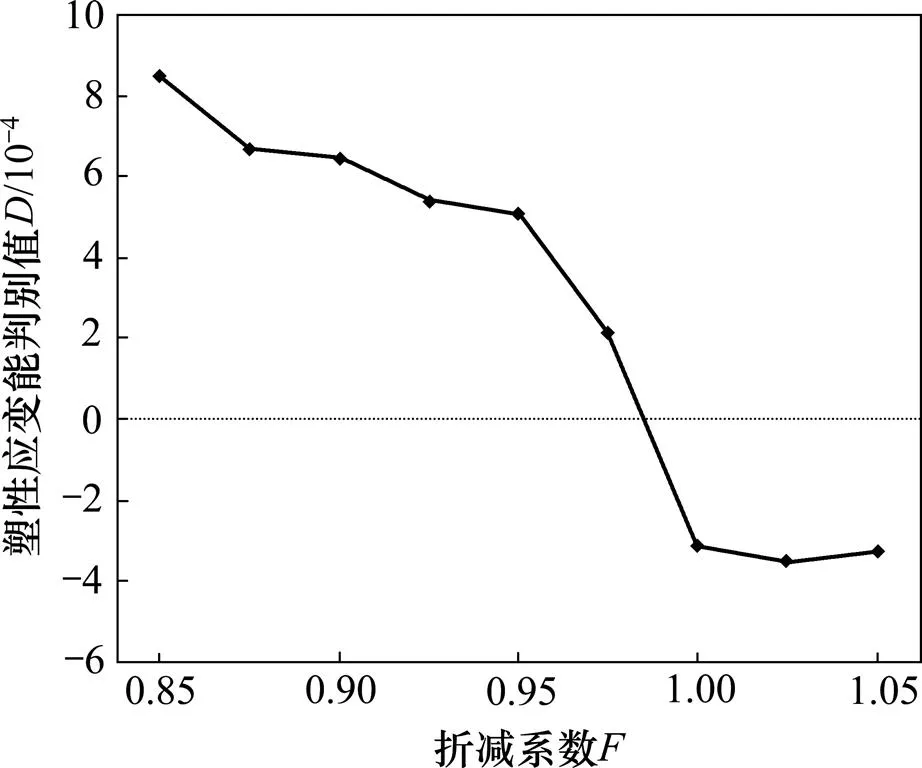
图4 单台阶坡体D与F的变化关系

表1 单台阶边坡极限平衡法安全系数计算结果

3.2 双台阶边坡算例

双台阶边坡的计算模型如图5所示。边坡参数取值如下：重度为20 kN/m3，体积模量为11.33 MPa，剪切模量为3.78 MPa，黏结力为11 kPa，摩擦角为23°。

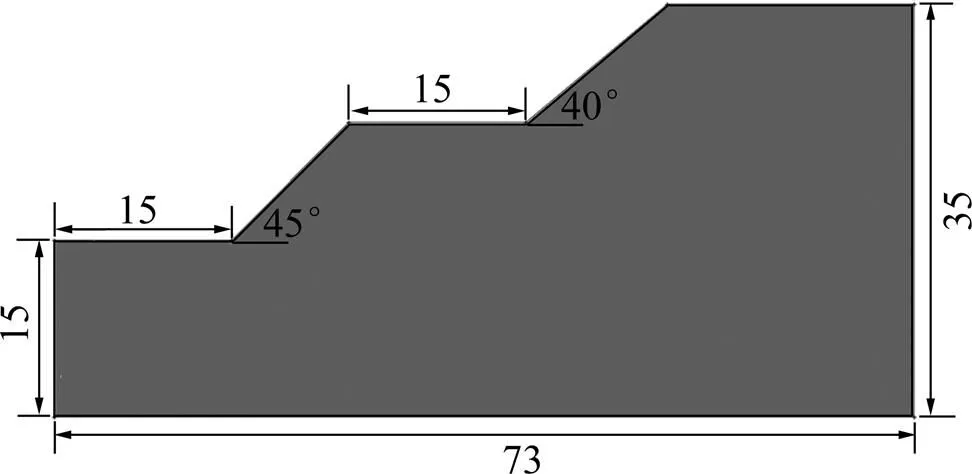
尺寸单位：m

通过强度折减法得到塑性应变能随折减系数的变化曲线如图6所示。由图6可知：塑性应变能随着折减系数的增大逐渐增大，在折减系数小于等于1.175时，增长趋势不明显，属于缓变段；折减系数在1.175~1.275范围内时，塑性应变能的增长趋势比缓变段要明显，属于渐变段；当折减系数大于等于1.300时，塑性应变能增长趋势较明显，属于骤变段。对突变理论对“塑性应变能−折减系数”曲线进行分析，得到塑性应变能判别值随折减系数变化曲线如图7所示。由图7可知：当折减系数小于等于1.275时，均大于0，表明坡体尚处于稳定状态；当折减系数大于等于1.30时，均小于0，表明坡体已处于失稳状态。图7中曲线与横轴的交点取值=1.287 5，此时=0，表明坡体恰好处于临界状态，因此，双台阶坡体计算模型的安全系数为1.287 5。采用7种极限平衡法对此单台阶坡体进行稳定性分析，各种方法对应的安全系数见表2。由表2可知：本文方法的计算结果与7种极限平衡法的计算结果较接近，其中与修正简布法所得结果最接近。

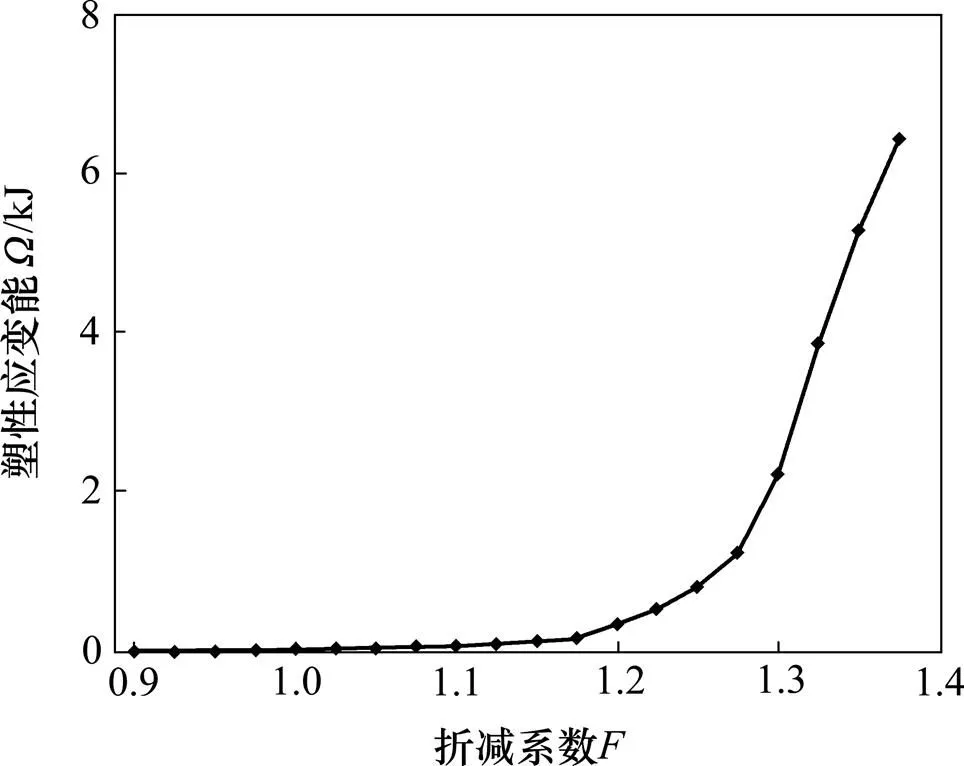
图6 双台阶坡体Ω与F的变化关系

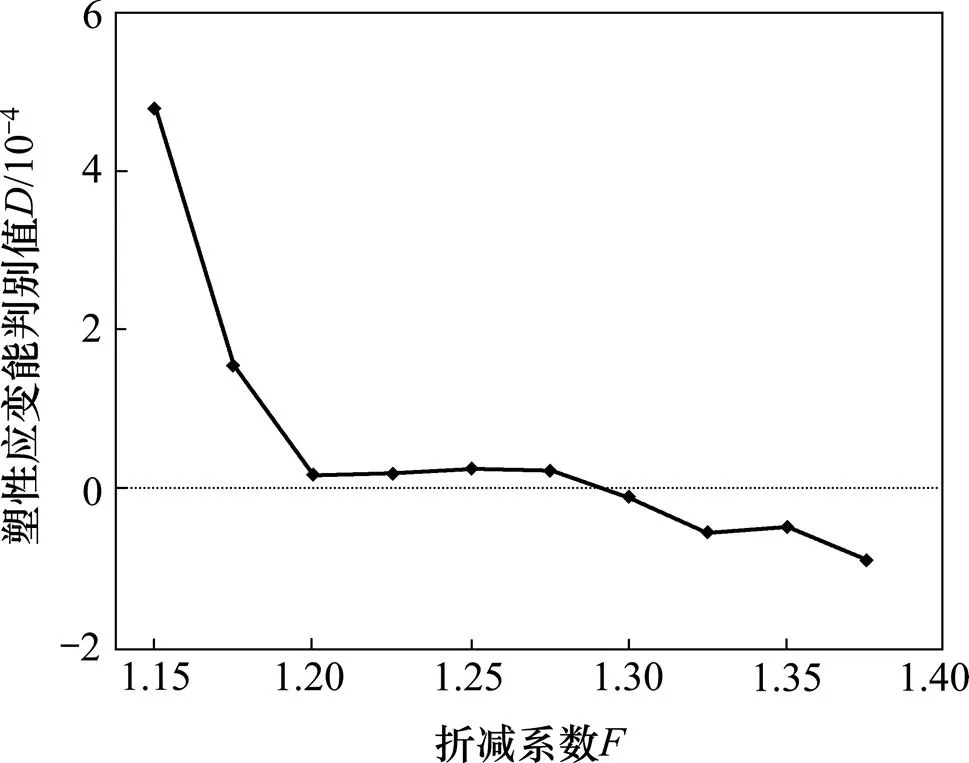
图7 双台阶坡体D与F的变化关系

表2 双台阶边坡极限平衡法安全系数计算结果

3.3 三台阶边坡算例

三台阶边坡的计算模型见图8。坡体参数取值如下：重度为25 kN/m3，体积模量为10.42 MPa，剪切模量为4.81 MPa，黏结力为16 kPa，摩擦角为22°。采用3.1和3.2节中的折减方法得到三台阶坡体的塑性应变能随折减系数的变化曲线，如图9所示。由图9可知：塑性应变能随着折减系数的增大逐渐增大，当折减系数小于等于1.075时，塑性应变能增长较缓慢；当折减系数大于等于1.1时，塑性应变能增长较明显。根据突变理论得到的塑性应变能判别值随折减系数变化曲线如图10所示。由图10可知：当折减系数小于等于1.125时，均大于0，表明此时坡体尚处于稳定状态；当折减系数大于等于1.15时，均小于零，表明此时坡体已处于不稳定状态。图10中曲线与横轴的交点取值=1.138，此时=0，表明坡体恰好处于临界状态，因此，根据突变理论确定的该三台阶坡体的安全系数为1.138。采用7种极限平衡法对此三台阶坡体进行稳定性分析，各种方法对应的安全系数见表3。由表3可知：本文方法的计算结果与7种极限平衡法的计算结果较接近，其中与修正简布法的结果最接近。

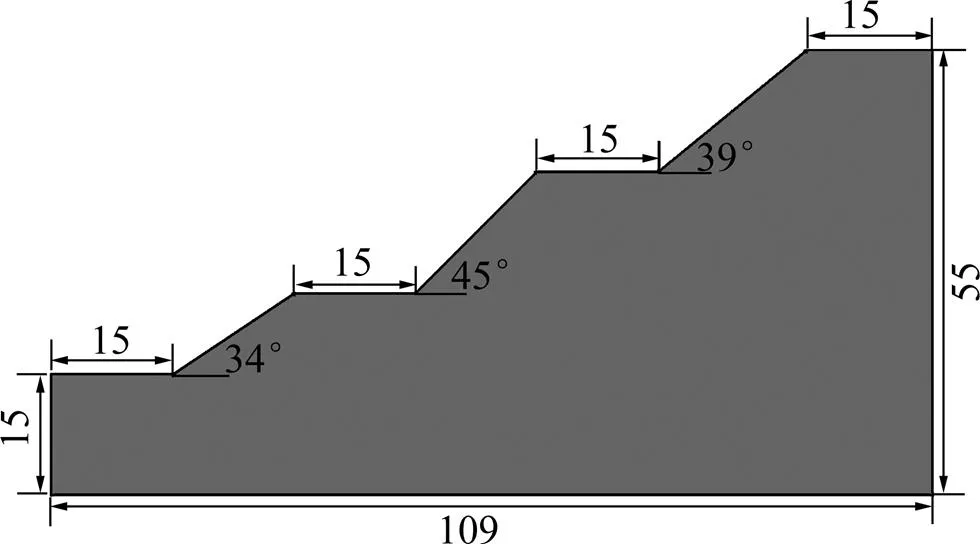
尺寸单位：m

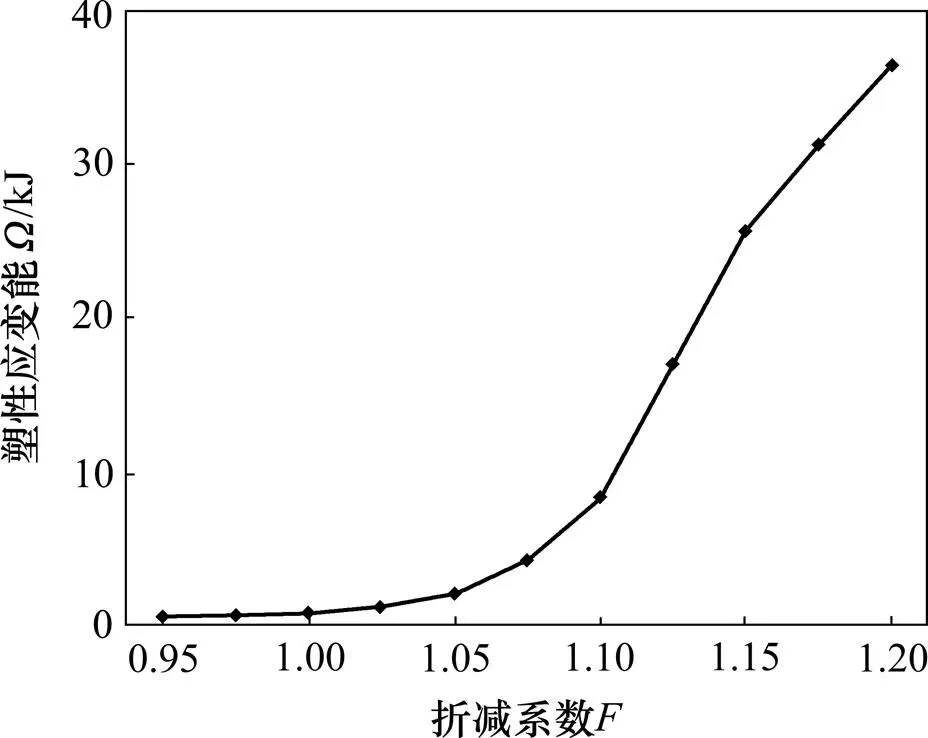
图9 三台阶坡体Ω与F的变化关系

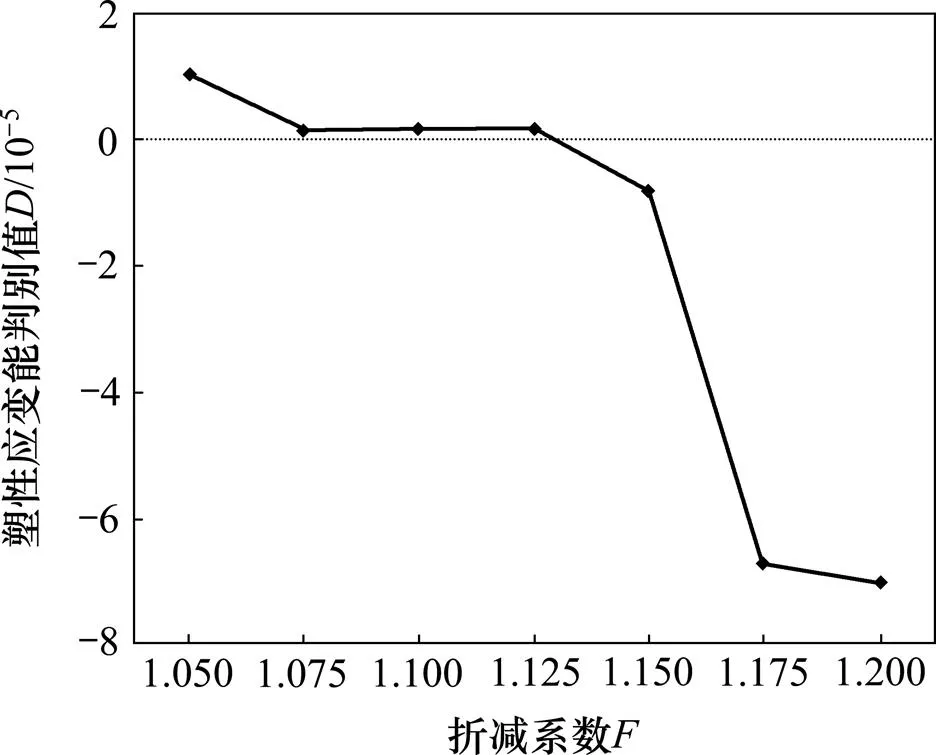
图10 三台阶坡体D与F的变化关系

表3 三台阶边坡极限平衡法安全系数计算结果

3.4 四台阶边坡算例

四台阶边坡的计算模型见图11。坡体参数取值如下：重度为25 kN/m3，体积模量为10.42MPa，剪切模量为4.81MPa，黏结力为56kPa，摩擦角为38°。

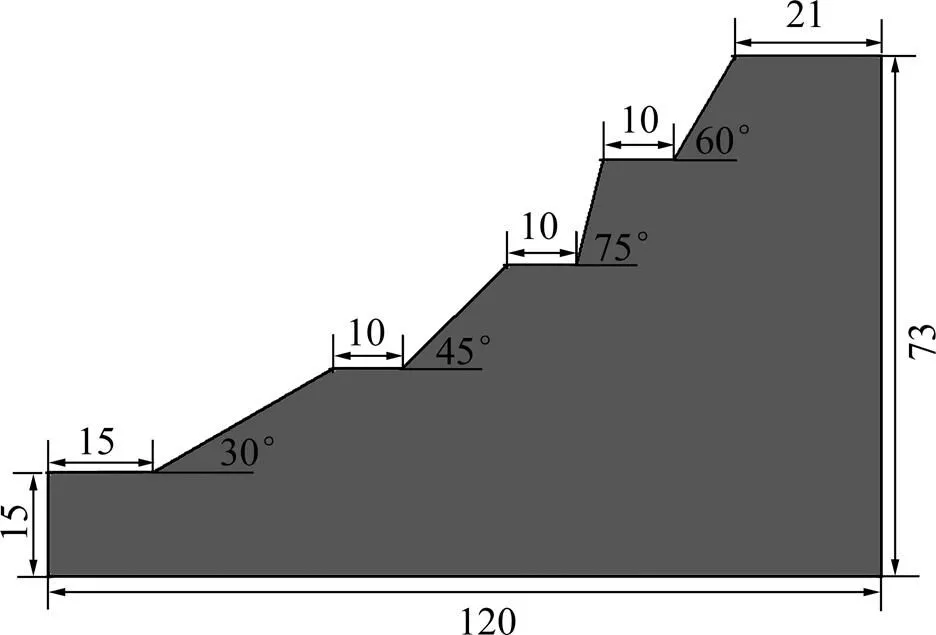
尺寸单位：m

采用前面3种台阶类型坡体相同的折减方法得到四台阶坡体的塑性应变能随折减系数的变化曲线如图12所示。由图12可知：塑性应变能大约在折减系数1.675附近出现突变，在此之前增长不明显，在此之后塑性应变能显著增大。为了具体确定塑性应变能发生突变的折减系数取值，下面通过尖点突变理论进行分析，得到四台阶坡体的塑性应变能判别值随折减系数变化曲线，见图13。由图13可知：当折减系数小于等于1.650时，均大于0，表明此时坡体尚处于稳定状态；当折减系数大于等于1.675时，均小于0，表明此时坡体已处于不稳定状态。图13中曲线与横轴的交点取值为=1.663，此时=0，表明坡体恰好处于临界状态，因此，根据突变理论确定的该四台阶坡体的安全系数为1.663。采用7种极限平衡法对此三台阶坡体进行稳定性分析，各种方法对应的安全系数见表4。由表4可知：本文方法的计算结果与7种极限平衡法的计算结果较接近，其中与修正简布法所得结果最接近。

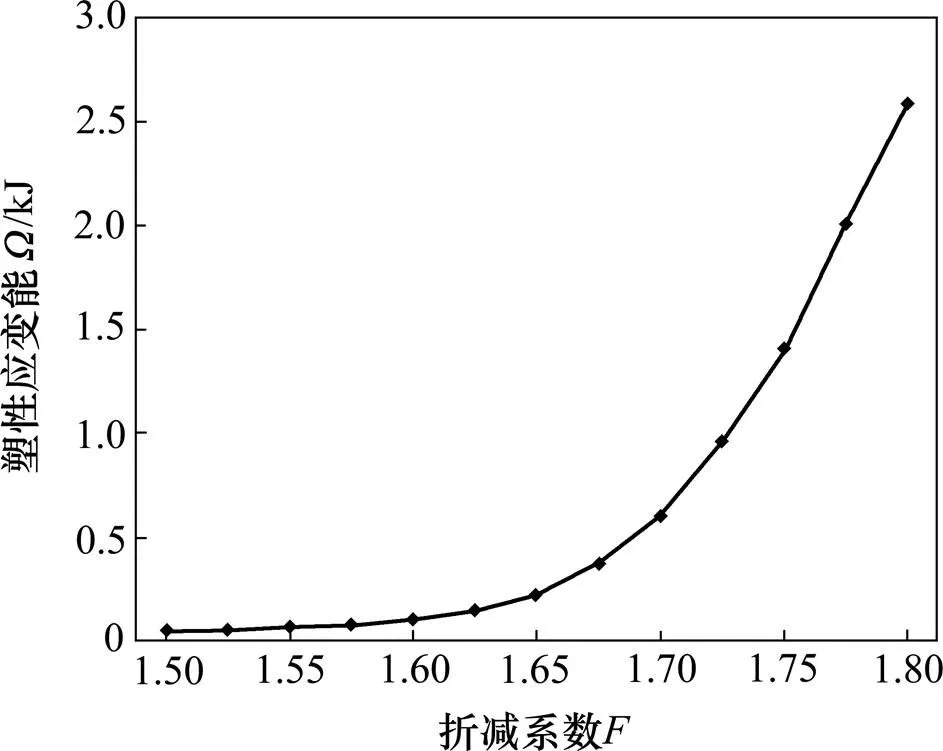
图12 四台阶坡体Ω与F的变化关系

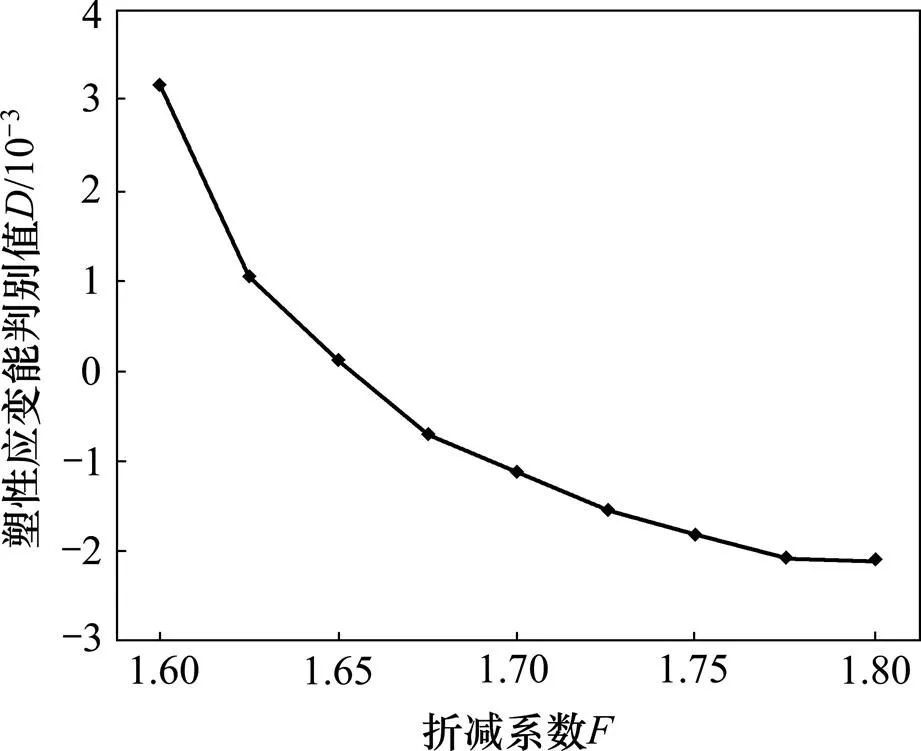
图13 四台阶坡体D与F的变化关系

表4 四台阶边坡极限平衡法安全系数计算结果

4 结论

1) 塑性应变能可以描述边坡整体的渐进破坏过程。随着折减系数的增大，整体塑性应变能也不断增大，当整体塑性应变能达到某个阀值(临界值)时，坡体或坝体发生滑动，此后，塑性区面积和塑性应变增大更明显，因此，整体塑性应变能也显著增大。

2) 塑性应变能可视为状态变量，用于表征坡体或坝体的发展状态，折减系数可视为控制变量，用于决定状态变量的取值。尖点突变理论可以表征塑性应变能的变化过程，并找出坡体发生突变时对应的折减 系数。

3) 塑性应变能发生突变的状态即为边坡失稳的临界状态，其发生突变时对应的折减系数即为边坡的最小安全系数。

4) 本文基于尖点突变理论和塑性应变能理论提出的坡体失稳临界状态判断方法可以很好地找到塑性应变能发生突变时对应的折减系数(即边坡的临界状态)，基于该方法得到的安全系数与极限平衡法得到的安全系数较接近，尤其与满足力平衡条件和力矩平衡条件的修正简布法所得结果最接近。

[1] YUAN Wei, BAI Bing, LI Xiaochun, et al. A strength reduction method based on double reduction parameters and its application[J]. Journal of Central South University, 2013, 20(9): 2555−2562.

[2] 赵尚毅, 郑颖人, 张玉芳. 极限分析有限元法讲座: Ⅱ有限元强度折减法中尾矿坝失稳的判据探讨[J]. 岩土力学, 2005, 26(2): 332−336. ZHAO Shangyi, ZHENG Yinren, ZHANG Yufang. Study on slope failure criterion in strength reduction finite element method[J]. Rock and Soil Mechanics, 2005, 26(2): 332−336.

[3] 郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡工程中的应用[M]. 北京: 人民交通出版社, 2011: 145−147. ZHENG Yingren, ZHAO Shangyi, LI Anhong, et al. EM limit analysis and its application in slope engineering[M]. Beijing: China Communication Press, 2011: 145−147.

[4] 林杭, 曹平, 宫凤强. 位移突变判据中监测点的位置和位移方式分析[J]. 岩土工程学报, 2007, 29(9): 1433−1438. LIN Hang, CAO Ping, GONG Fengqiang. Analysis of location and displacement modes of monitoring points in displacement mutation criteria[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1433−1438.

[5] 袁维. 强度折减法的若干研究[D]. 武汉: 中国科学院武汉岩土力学研究所, 2014: 85−95. YUAN Wei. Studies on the strength reduction method[D]. Wuhan: Chinese Academy of Sciences. Institute of Rock and Soil Mechanics, 2014: 85−95.

[6] 陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J]. 岩石力学与工程学报, 2014, 33(2): 243−252. CHEN Guoqing, HUANG Runqiu, SHI Yuchuan, et al. Stability anlysis of slope based on dynamic and whole strength reduction methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 243−252.

[7] 陈力华, 靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报, 2012, 45(9): 136−146. CHEN Lihua, JI Xiaoguang. Study on the applicability of three criteria for slope instability using finite element strength reduction method[J]. China Civil Engineering Journal, 2012, 45(9): 136−146.

[8] 张爱军, 莫海鸿. 有限元强度折减法中边坡失稳位移突变判据的改进[J]. 岩土力学, 2013, 34(S2): 332−338. ZHANG Aijun, MO Haihong. Improving displacement mutation criterion of slope failure in strength reduction finite element method[J]. Rock and Soil Mechanics, 2013, 34(S2): 332−338.

[9] 吴伯建, 朱珍德, 顾祖军. 有限元强队折减法进行土坡稳定分析的精度研究[J]. 水利与建筑工程学报, 2013, 11(1): 324−329. WU Bojian, ZHU Zhende, GU Zujun. Study on accuracy of soil slope stability analysis based on strength reduction FEM[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(1): 324−329.

[10] 徐晓阳, 姜晓日, 李宁波. 改进的收敛性判据在边坡稳定分析中的应用[J]. 水文地质工程地质, 2014, 41(1): 79−84. XU Xiaoyang, JIANG Xiaori, LI Ningbo. Improve the convergence criterion in the application of the slope stability analysis[J]. Hydrogeology & Engineering Geology, 2014, 41(1): 79−84.

[11] 施建勇, 曹秋荣, 周璐翡. 修正有限元强度折减法与失稳判据在边坡稳定分析中的应用[J]. 岩土力学, 2013, 34(S2): 237−241. SHI Jianyong, CAO Qiurong, ZHOU Lufei. Modified finite element method for shear strength reduction and its instability criterion in slope stability analysis[J]. Rock and Soil Mechanics, 2013, 34(S2): 237−241.

[12] YANG Guanghua, ZHONG Zhihui, FU Xudong, et al. Slope analysis based on local strength reduction method and variable-modulus elasto-plastic model[J]. Journal of Central South University, 2014, 21(5): 2041−2050.

[13] DONG Tianwen, ZHENG Yinren. Limit analysis of vertical anti- pulling screw pile group under inclined loading on 3D elastic-plastic finite element strength reduction method[J]. Journal of Central South University, 2014, 21(3): 1165−1175.

[14] 周元辅, 邓建辉, 崔玉龙, 等. 基于强度折减法的三维边坡失稳判据[J]. 岩土力学, 2014, 35(5): 1430−1437. ZHOU Yuanfu, DENG Jianhui, CUI Yulong, et al. Instability criterion of three-dimensional slope based on strength reduction method[J]. Rock and Soil Mechanics, 2014, 35(5): 1430−1437.

[15] 郑颖人. 岩土塑性力学的新进展: 广义塑性力学[J]. 岩土工程学报, 2003, 25(1): 1−9. ZHENG Yingren. New development of geotechnical plastic mechanics: generalized plastic mechanics[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(1): 1−9.

[16] 郑颖人, 孔亮. 广义塑性力学及应用[J]. 中国工程科学, 2005, 7(11): 21−37. ZHENG Yingren, KONG Liang. Generalized plastic mechanics and its application[J]. Engineering Science, 2005, 7(11): 21−37.

[17] 张业民. 突变理论在岩土与结构工程中的若干应用[D]. 大连: 大连理工大学土木水利学院, 2008: 102−108. ZHANG Yemin. Catastrophe theory applied in several geotechnic and structure engineering area[D]. Dalian: Dalian University of Technology. School of Civil and Hydraulic Engineering, 2008: 102−108.

[18] 夏开宗, 刘秀敏, 陈从新, 等. 考虑突变理论的顺层岩质边坡失稳研究[J]. 岩土力学, 2015, 36(2): 477−486. XIA Kaizong, LIU Xiumin, CHEN Congxin, et al. Analysis of mechanism of bedding rock slope instability with catastrophe theory[J]. Rock and Soil Mechanics, 2015, 36(2): 477−486.

[19] 付成华, 陈胜宏. 基于突变理论的地下工程洞室围岩失稳判据研究[J]. 岩土力学, 2008, 29(1): 167−173. FU Chenghua, CHEN Shenghong. Study on instability criteria of surrounding rock of underground engineering cavern based on catastrophe theory[J]. Rock and Soil Mechanics, 2008, 29(1): 167−173.

[20] 赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报, 2010, 29(7): 1424−1434. ZHAO Yanlin, WU Qihong, WANG Weijun, et al. Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1424−1434.

[21] DONALD I B, GIAM P. The ACADS slope stability programs review[C]// Proc 6th International Symposium on Landslides. Christchurch, New Zealand, 1992: 1665−1670.

[22] 李小春, 任伟, 王少泉, 等. 论金属矿山排土场设计规范中边坡极限平衡计算方法的选取[J]. 岩石力学与工程学报, 2011, 30(S2): 4136−4142. LI Xiaochun, REN Wei, WANG Shaoquan, et al. Selection of limit equilibrium methods in the design specification for waste dump of metal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 4136−4142.

An approach for determination of slope failure criterion based on plastic energy and mutation theory

LI Zhiping1, 2, PENG Zhenbin1, HE Zhongming3, TANG jia1

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. Changsha Design and Research Institute of Ministry of Chemical Industry, Changsha 410117, China; 3. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China)

Considering that each kinds of failure criterion have their advantages and disadvantages, a new slope failure criterion associated with strength reduction method was proposed based on the plastic strain energy theory and the mutation theory. Plastic energy was regarded as an index to evaluate the whole stability of the slope and cusp catastrophic model was taken as a criterion to judge the stable state of the slope. During the process of the adjustment of reduction coefficient, the plastic strain energy of whole slope model corresponding to each reduction factor was recorded to establish the “plastic strain energy-reduction factor” curve, and then the reduction factor corresponding to the mutation of plastic strain energy was studied using mutation theory; this reduction factor was considered as the safety factor of the slope. At last, the reliability of the proposed method was verified through calculation examples of single step slope and multiple steps slope. The results indicate that the safety factor acquired by the proposed method is very close to the one acquired by the limit equilibrium method, especially close to the factor acquired by the corrected Janbu method.

strength reduction method; slope stability; safety factor; failure criterion; plastic strain energy; mutation theory

10.11817/j.issn.1672-7207.2016.09.038

TU452

A

1672−7207(2016)09−3193−08

2016−01−20；

2016−03−12

国家自然科学基金资助项目(51508042) (Project(51508042) supported by the National Natural Science Foundation of China)

彭振斌，教授，博士生导师，从事尾矿坝及岩土工程技术研究；E-mail: zbpz9040@sina.com

(编辑 陈灿华)