不同卸荷路径下大理岩破坏过程能量演化规律

丛宇，王在泉，郑颖人，冯夏庭，张黎明



不同卸荷路径下大理岩破坏过程能量演化规律

丛宇1, 2，王在泉2，郑颖人3，冯夏庭1，张黎明2

(1. 中国科学院武汉岩土力学研究所，湖北武汉，430071；2. 青岛理工大学理学院，山东青岛，266033；3. 后勤工程学院建筑工程系，重庆，400041)

为寻找破坏过程中能量的实时演化规律，对大理岩进行不同路径的加、卸载试验，探讨岩体轴向能量、实际吸收的总能量随应变的演化规律。研究结果表明：在不同应力路径下，岩样轴向能量随应变的增加而呈非线性增大，初期能量增长速率较小，随后速率慢慢增大，在达到岩样临界破坏点时，出现1个速率的拐点，随后增长速率趋于稳定；在不同应力路径下，岩样破坏的轴向能量−应变曲线与总能量−应变曲线都存在1个速率突然变化的拐点，轴向能量的拐点出现在对应应力−应变曲线的破坏处，而总能量的拐点出现在对应峰值处。围压的变化没有改变不同路径下岩样的轴向能量−应变曲线的形式，但在不同围压下，加轴压、卸围压路径的总能量−应变曲线呈现不同的形式。卸围压速率没有改变轴向能量与总能量曲线的形式，只是改变曲线在不同阶段的变化速率。围压的增大，不同路径下岩样的轴向能量与总能量差增大，而卸荷速率的影响正好相反。

能量演化；应力路径；卸围压；拐点

应力−应变作为特定力学状态的描述手段，只是热力学状态某一方面的表征，单纯依靠应力−应变关系建立强度准则或以其大小作为破坏判据很难真实反映岩石的破坏规律。从热力学角度可知，物质的破坏不过是能量驱动下的一种状态失稳现象[1]。因此，抓住岩体变形破坏的能量本质，详细分析岩体变形破坏过程能量的演化规律，建立以能量为基础的岩样强度准则、破坏判据，就有可能更真实地反映岩体的变形破坏规律，服务于工程实践。在强度与破坏准则方面：王学滨等[2]对单轴压缩岩样推导出基于能量原理的剪切破坏失稳判据；高红等[3]推导出适合岩土材料的三剪能量准则。LI[4]认为材料黏结强度决定试样破坏的弹性能密度，决定了材料的破坏形式，有可能定义材料的失效准则。在试验分析方面，陈卫忠等[5]认为岩石在破坏前所能够储存的最大应变能受围压和卸载速率的控制；刘建峰等[6]开展了对细砂岩和粉砂质泥岩的单轴压缩循环荷载试验，认为岩石密度越大，滞回环面积越小，岩石发生的能量耗散越小，反之越大。在演化过程方面，尤明庆等[7]对粉砂岩进行单轴压缩、卸围压试验，并简单分析了试验过程中能量的演化规律，认为岩样破裂时实际吸收的能量与破裂所处的围压成线性关系，而试验应力路径对此影响并不是很明显；张志镇等[8]对红砂岩进行不同加载速率下单轴压缩试验，得到加载过程中能量的演化规律。由此可以看出[9−11]：基于能量原理，现有岩体破坏研究分析集中在理论应用与试验分析，而试验的研究主要集中在某阶段的能量值对比上，忽视了试验过程中能量的演化规律，即使有对能量演化过程的研究，也局限于单轴压缩等简单应力路径。目前，对于复杂路径下岩样能量的演化规律研究并不多见，而岩石的破坏更趋向于一种过程性破坏、一种过程性的累计变化，不能仅仅考虑某一阶段的能量。研究岩样试验过程的能量演化过程更有助于探索复杂路径下岩样的损伤、破坏机制与能量的本质联系，有助于进一步完善岩石失稳、破坏准则，服务于工程实践[11]。因此，本文作者对大理岩进行不同路径下加、卸载试验，结合不同阶段能量具体值，获得不同路径下岩样轴向吸收的能量、岩样实际吸收的总能量的演化过程规律，并进一步得到不同路径下围压、卸荷速率对能量演化过程的影响，研究结果对岩石破坏机制、岩爆灾害机制等都有着积极的意义。

1 试验概况

试验采用的大理石岩样均同批次采自河南驻马店，细粒结构，质地细腻均匀。按照国际岩石力学试验要求，在实验室内将岩样加工成直径为50 mm、高为100 mm的圆柱体，并对两端仔细研磨。为了尽可能降低试验的离散性，试验前对岩样进行了2步筛选：首先剔除明显含有节理的岩样，然后选取波速约为4 500 m/s的岩样。

试验加载系统在中国矿业大学MTS815.02型电液伺服岩石力学试验机上完成。试验采用2种方案。

1.1 常规三轴加荷试验

试验分2个阶段：按静水压力条件施加围压至设定值(0，10，20，30和40 MPa)；围压不变，以位移速度0.003 mm/s施加轴向应力至岩样破坏。

1.2 加轴压、卸围压试验

试验分3个阶段：按静水压力条件施加围压(10，20，30和40 MPa)；围压不变，提高轴向应力至岩样峰值前的60%；以位移速度0.003 mm/s施加轴向应力，同时以某一速度(0.2，0.4，0.6和0.8 MPa/s)卸围压直到岩样被破坏。

作功是能量由一种形式转化为另一种形式的过程，而作功的2个必要因素为：作用在物体上的力和物体在力的方向上通过的距离，基于此，通过对试验得到的应力与应变作功进行计算，从而得到大理岩破坏过程中的能量演化规律。岩样吸收的轴向能量定义为试验机对岩样轴向作功为

三轴应力状态下岩样实际吸收的总能量T为

2 不同路径破坏过程中能量演化规律

图1~3所示分别为大理岩单轴、常规三轴及加轴压卸围压路径下大理岩破坏的应力−应变曲线、试验机对岩样作功而得到的轴向能量−应变曲线、三轴应力状态下岩样实际吸收的总能量−应变曲线。破坏点是指在应力−应变曲线中，峰后应力突然下降时对应的应变处，文中所涉及的能量指单位体积能量。

图1所示为不同应力路径试验得出的应力−应变，与已有结论[12]相符，大致经历4个阶段：压密阶段、线弹性阶段、屈服弱化阶段和点之后的破坏阶段。

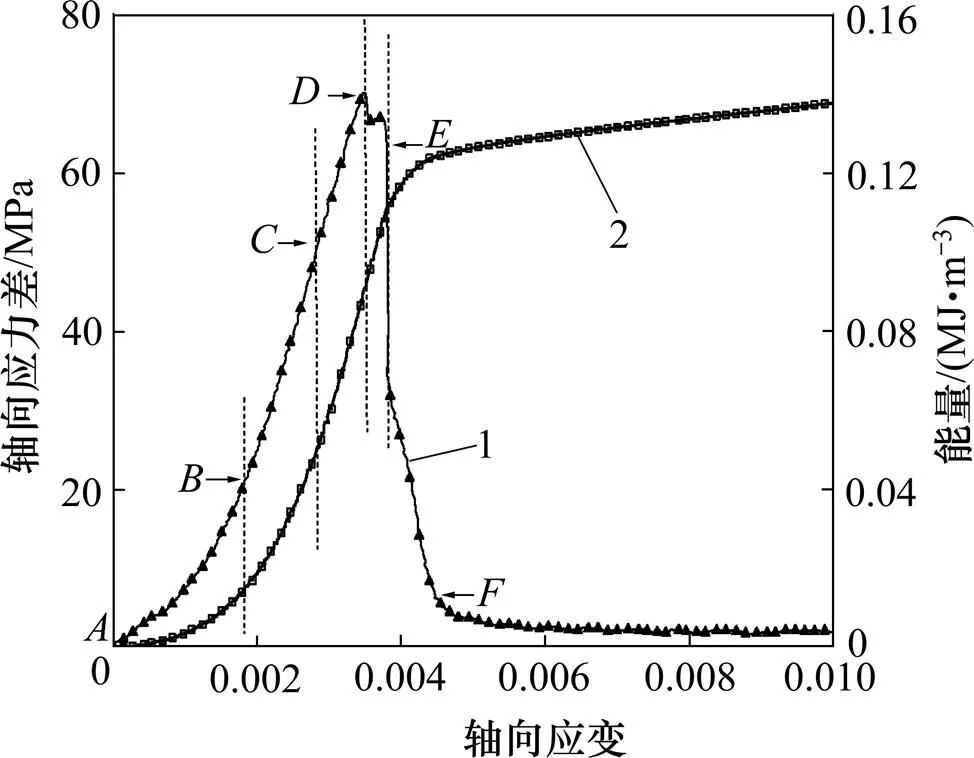
1—应力−应变曲线；2—轴向能量−应变曲线。

单轴压缩破坏路径如图1所示。由图1可知：对应压密段的轴向能量曲线2，曲线2以较小的增长速率非线性增大至0.016 MJ/m3；岩样在能量曲线2中的线弹性段，内部原有微裂隙压实，裂隙尖端应力集中导致微裂纹萌生、扩展等，在这个过程中依旧消耗少量能量，因而并不会是完全意义上的弹性，能量曲线抛物线增加，同时增长速率逐渐增大，能量增大至0.054 MJ/m3；能量曲线对应的屈服弱化段，岩样环向变形增加较快但轴向应力增加变慢，岩样内部裂纹贯通以及宏观裂纹的产生、扩展都进一步增加了耗散能，提高了耗散能在能量分配中所占的比例；峰前段，曲线大致呈线性增大，增长速率基本稳定；峰后段，增长速率降低，直至破坏点对应处，曲线的增长速率发生明显的变化，形成拐点，在处为0.11 MJ/m3，点后岩样的环向变形随轴向变形迅速增加，出现剪切破坏面，岩样破裂，岩样吸收的能量其实主要是用于内部塑性滑移而产生的摩擦能的耗散，达到点后能量曲线2增长速率较稳定。

常规三轴破坏路径如图2所示。由图2可知：能量曲线2与3的压密段，岩样吸收的能量基本全用于初始裂纹的闭合、摩擦滑移等，两者基本重合，曲线能量值均增大至0.01 MJ/m3；能量曲线2与3的线弹性段，曲线的整体增大规律与图1所示的规律相似，但图2中能量曲线2增长速率逐渐大于曲线3的增长速率，曲线3的能量增大至0.05 MJ/m3的同时，曲线2只增大至0.06 MJ/m3；轴向能量曲线2的屈服弱化段，规律与图1所示规律相似，能量增大至0.25 MJ/m3，同时存在1个速率突然变化的拐点；而总能量曲线3的峰前段，与曲线2之间的差距进一步增大，增长速率进一步减小；峰后段，曲线3负向增大至 0.11 MJ/m3；段，能量曲线2与3的增长速率都降低，但曲线3的速率明显比曲线2的速率高，至点时两者速率都维持稳定。

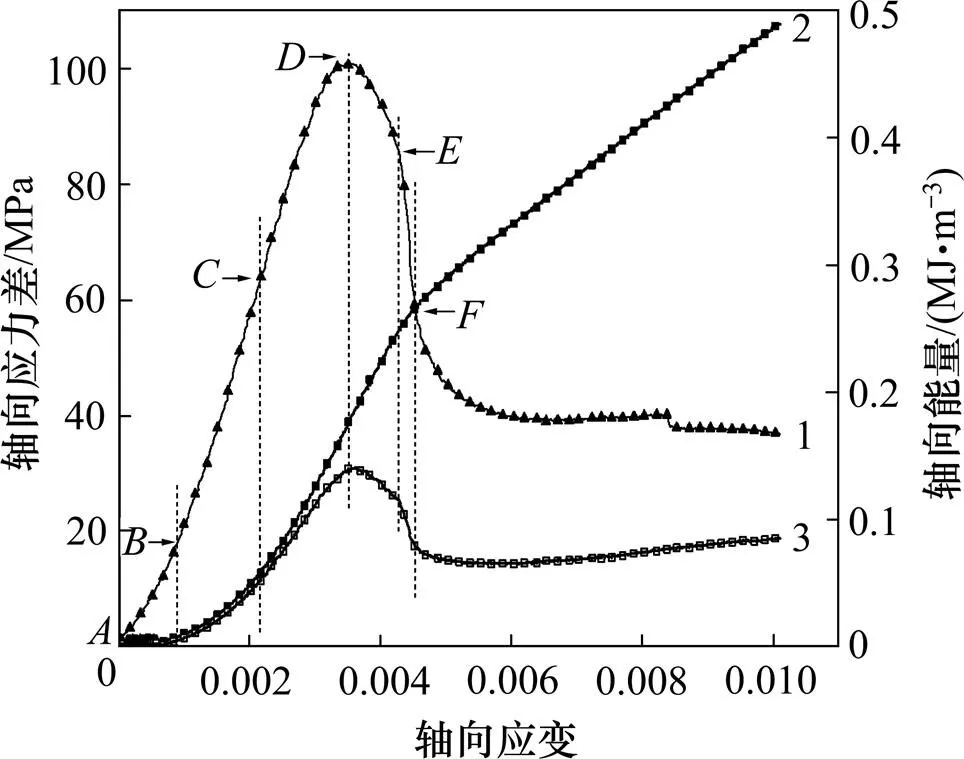
1—应力−应变曲线；2—轴向能量−应变曲线；3—总能量−应变曲线。

加轴压、卸围压路径如图3所示。由图3可知：对应压密段的能量曲线2与3，能量增大至 0.012 MJ/m3，曲线规律与图2所示规律相似；曲线2与3的线弹性段，曲线3的能量增大至0.085 MJ/m3，曲线2增大至0.095 MJ/m3，增大规律与图2所示规律相似；能量曲线2与能量曲线3的屈服弱化段，两者基本都呈直线增大至点，曲线2的能量增大至0.155 MJ/m3，曲线3的能量达到0.140 MJ/m3，但曲线间差距逐渐增大，曲线2存在1个增长速率的拐点；点后，曲线2与曲线3能量增长速率迅速降低，但保持稳定。图1~3所示路径试验的岩样破坏图如图4所示。

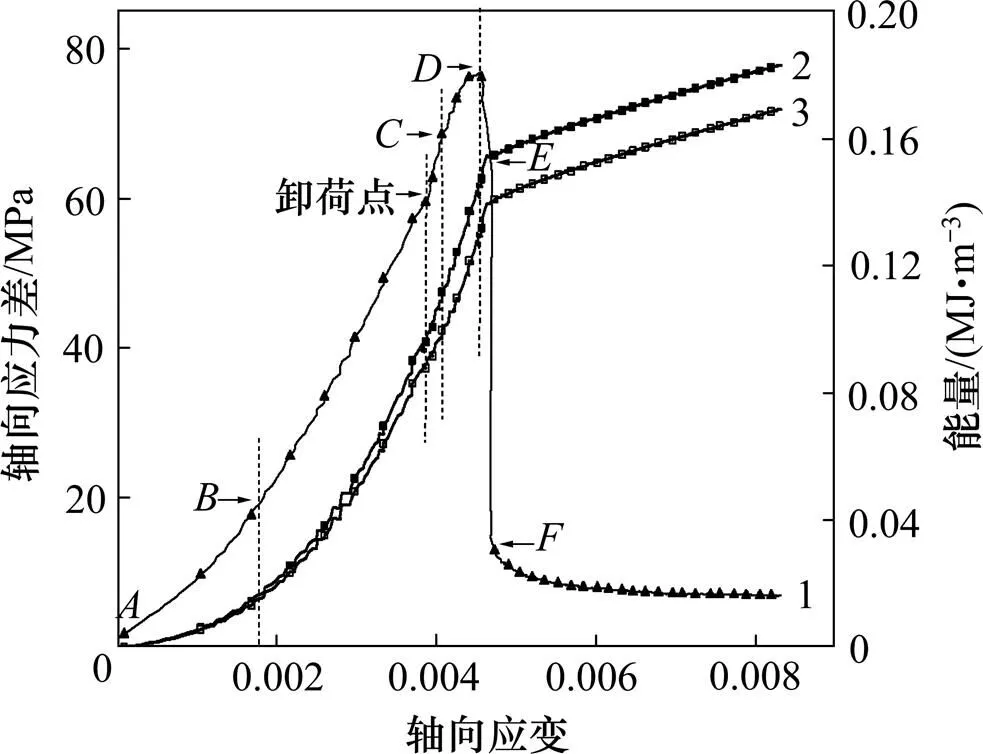
1—应力−应变曲线；2—轴向能量−应变曲线；3—总能量−应变曲线。

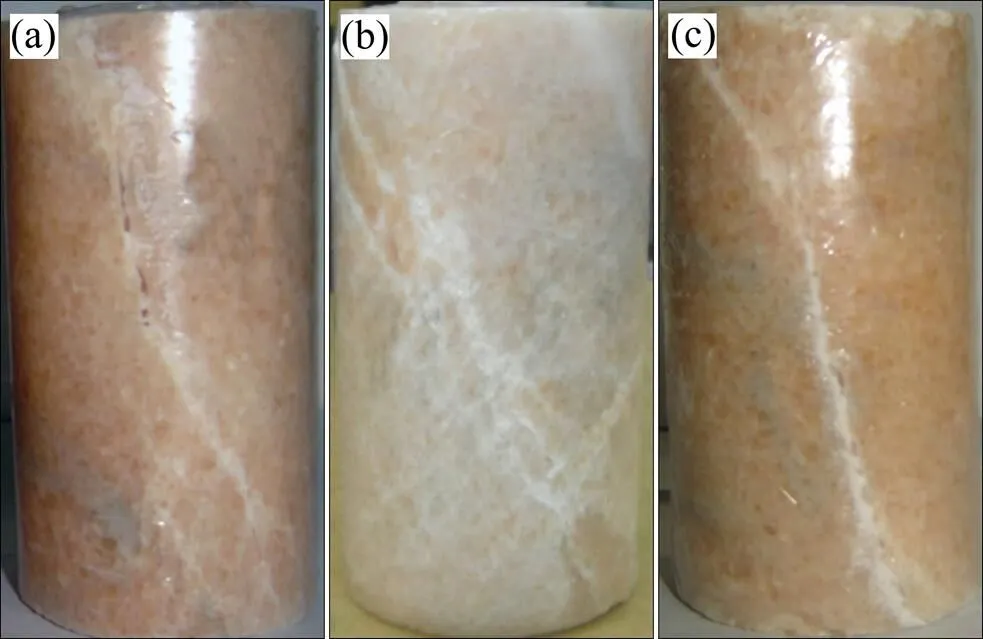
(a) 单轴；(b) 常规三轴；(c) 加轴压、卸围压

由图4可以看出：应力路径对轴向能量−应变曲线的整体变化趋势影响很小，但会改变轴向能量在不同阶段的增长速率；而在总能量−应变曲线方面，不同的应力路径既影响曲线的变化趋势，又会改变总能量在不同阶段的增长速率。

3 不同路径破坏过程中围压的影响

3.1 常规三轴破坏过程

常规三轴试验的具体结果如表1所示，将表1中特殊点能量值整理成图5。表1所示的破坏点是指岩样峰后屈服破坏，承载力明显降低的部位。图6所示为30 MPa围压下岩样加载破坏的能量演化曲线。

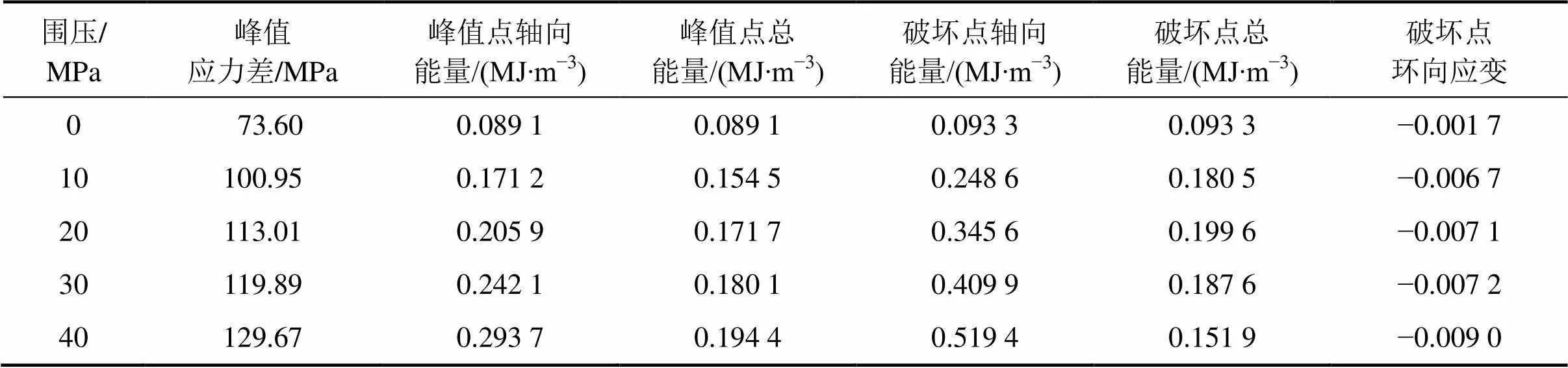
表1 常规三轴试验结果

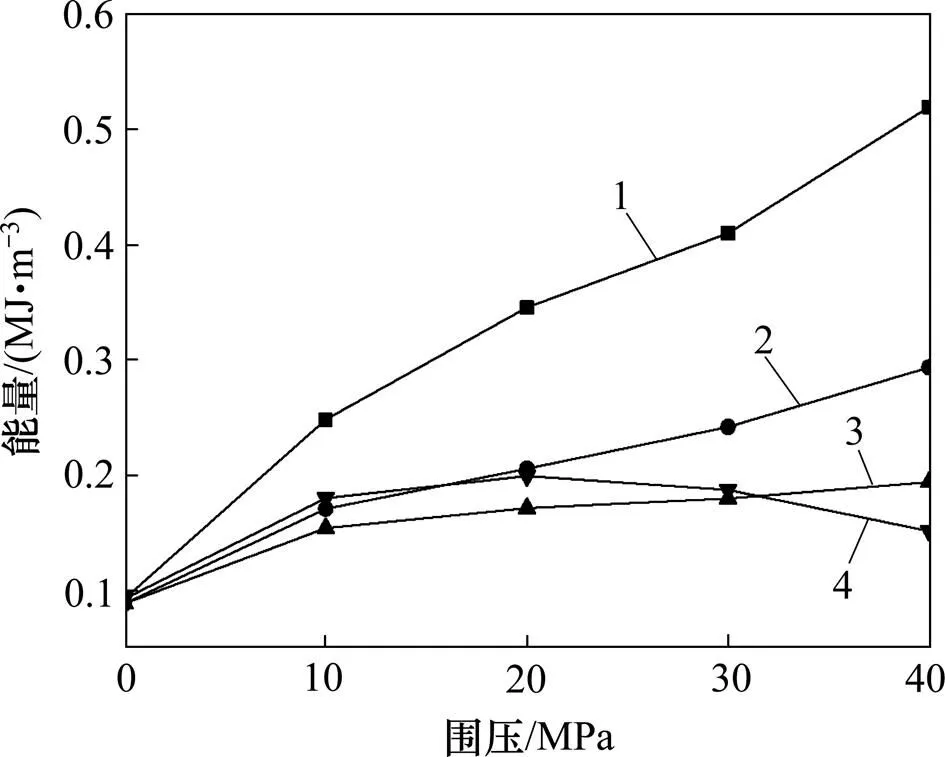
1—破坏点轴向能量−围压曲线；2—峰值点轴向能量−围压曲线；3—峰值点总能量−围压曲线；4—破坏点总能量−围压曲线。

1—应力−应变曲线；2—轴向能量−应变曲线；3—总能量−应变曲线。

由图2与图6可知：围压最显著的影响体现在承载力峰值点附近，围压越低，岩样破坏越突然，岩样的残余承载能力越低，岩样峰值应力差越低，峰后应变变化率越高，破坏时的应变也相对较高。

围压没有改变轴向能量−应变曲线的整体演化趋势，但其改变了该曲线进入弹性阶段的增大率。岩样要达到与低围压相同的应变，为了克服高围压的影响，高围压岩样内部裂纹发生不稳定的扩展、贯通、塑性滑移等就需要消耗更多的能量，因而峰值处、破坏点处的轴向能量较高。围压的影响见图5中的曲线1和2。

岩样总能量值见表1，围压对总能量值影响见图5中的曲线3和4。由图5与表1可以看出：总能量−应变曲线趋势上也基本没有随围压变化出现太明显的波动，但高围压岩样曲线3的峰后负向增大率越大，峰值点的总能量也会增大，岩样消耗能量随围压而增多，导致破坏点的总能量出现减小的趋势。

据图5中曲线2与曲线3在不同应变时的能量差，可以得出岩样在不同应变时内部消耗的能量。弹性阶段前能量差基本接近0 MJ/m3；进入塑性阶段后，能量差逐渐增大；围压从10 MPa增加到40 MPa，在破坏点处能量差从0.068 1 MJ/m3增加到0.367 5 MJ/m3，表明岩样在塑性阶段出现明显能量消耗。围压增加，常规三轴路径峰前能量差逐渐增大，峰后能量差的变化更加明显。

3.2 加轴压、卸围压破坏过程

岩样峰前60%处，0.6 MPa/s的速率在不同围压下进行加轴压、卸围压破坏试验的具体结果如表2所示。对表2中的具体结果处理如图7所示。图8所示为30 MPa围压下岩样卸围压的能量演化曲线。

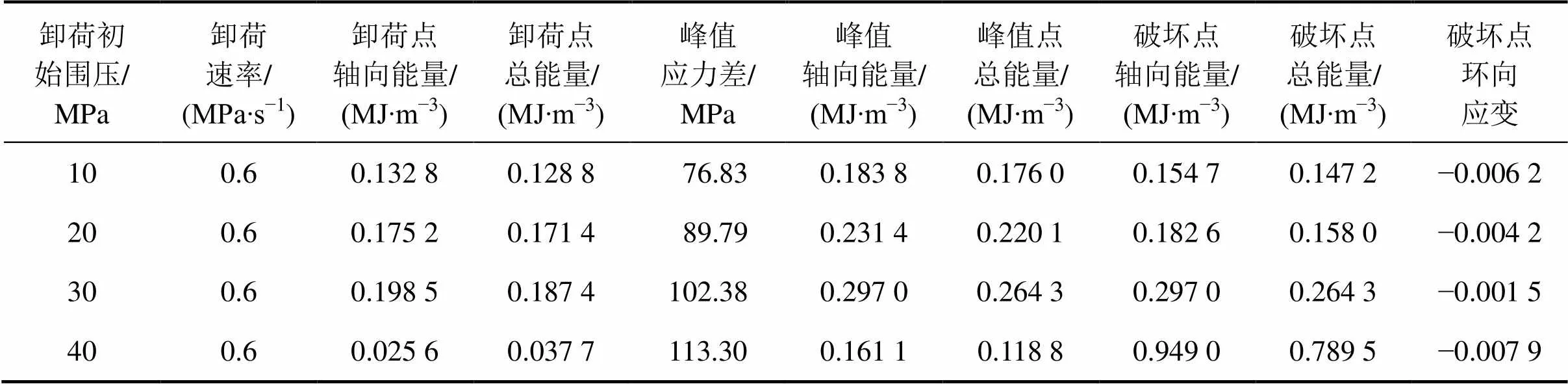
表2 不同围压卸载试验结果

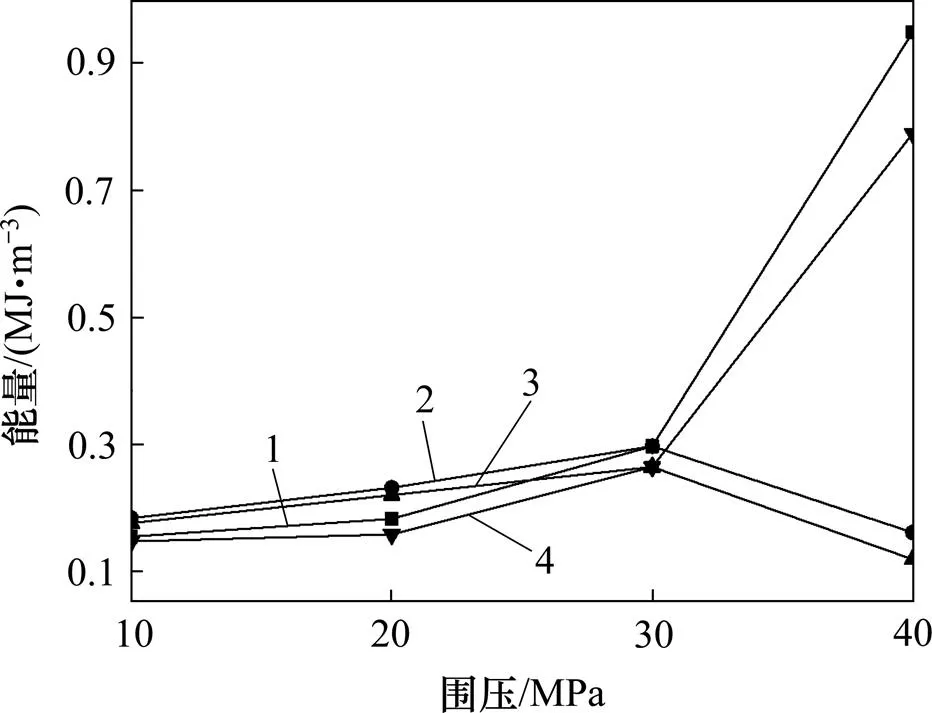
1—破坏点轴向能量−围压曲线；2—峰值点轴向能量−围压曲线；3—峰值点总能量−围压曲线；4—破坏点总能量−围压曲线。

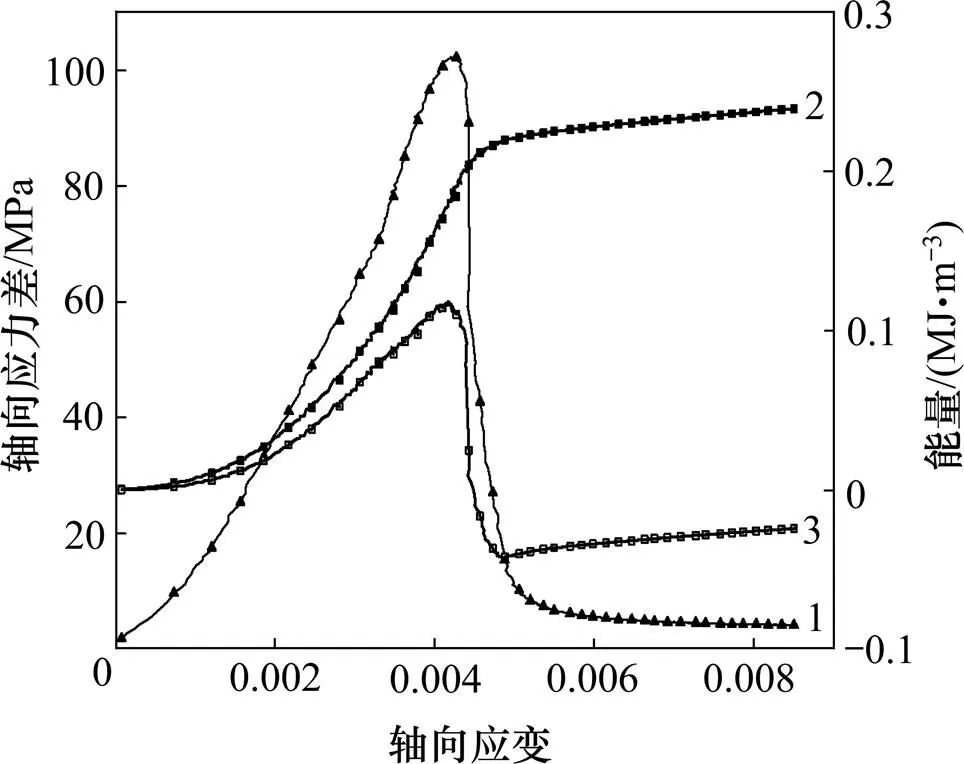
1—应力−应变曲线；2—轴向能量−应变曲线；3—总能量−应变曲线。

由图3与图8可知：围压对应力−应变曲线的影响主要体现在随围压的增大，岩样的峰值轴向应力差逐渐增大，应力−应变曲线的塑性应变逐渐增大，趋于塑性流动。规律与常规三轴路径得出规律相似，表明围压对应力−应变曲线的影响不随路径的变化而变化。峰值应力差、破坏点环向应变见表2。

加轴压、卸围压路径下围压对轴向能量−应变曲线2增大率的影响要比常规三轴路径的影响更明显，特别是在破坏点附近。随着围压增加，破坏点处附近的拐点由低围压曲线2时的非常明显变得平缓。表2中不同特殊点的轴向能量表明除了围压40 MPa外，随着围压增加，岩样的轴向能量都会增加，如图7所示的破坏点与峰值点的轴向能量−围压曲线。加轴压、卸围压路径与常规三轴路径围压的影响规律类似。

高围压(30，40 MPa)与低围压(10，20 MPa)时总能量−应变曲线变化趋势不同。高围压时曲线拐点在峰值点附近，低围压时曲线在破坏点附近出现拐点，围压越高，拐点越平缓。从表2中具体的总能量及图7中的破坏点的轴向能量−围压曲线、破坏点的总能量−围压曲线也可以看出，在破坏点处，岩样围压增大，总能量逐渐增大，这与常规三轴的规律不一样。

加轴压、卸围压路径下围压对能量差的影响与常规三轴路径一样，随围压的增大，能量差逐渐增大，当围压为10 MPa时，能量差为0.007 5 MJ/m3，而当围压为40 MPa时，能量差为0.159 4 MJ/m3，表明能量差的变化与围压有关，与路径无关。

4 加轴压、卸围压破坏过程中卸荷速率影响

不同卸荷速率下岩样在峰前60%处，30 MPa的围压进行加轴压、卸围压破坏试验的具体结果如表3所示。对表3中的具体结果进行处理，结果如图9所示。

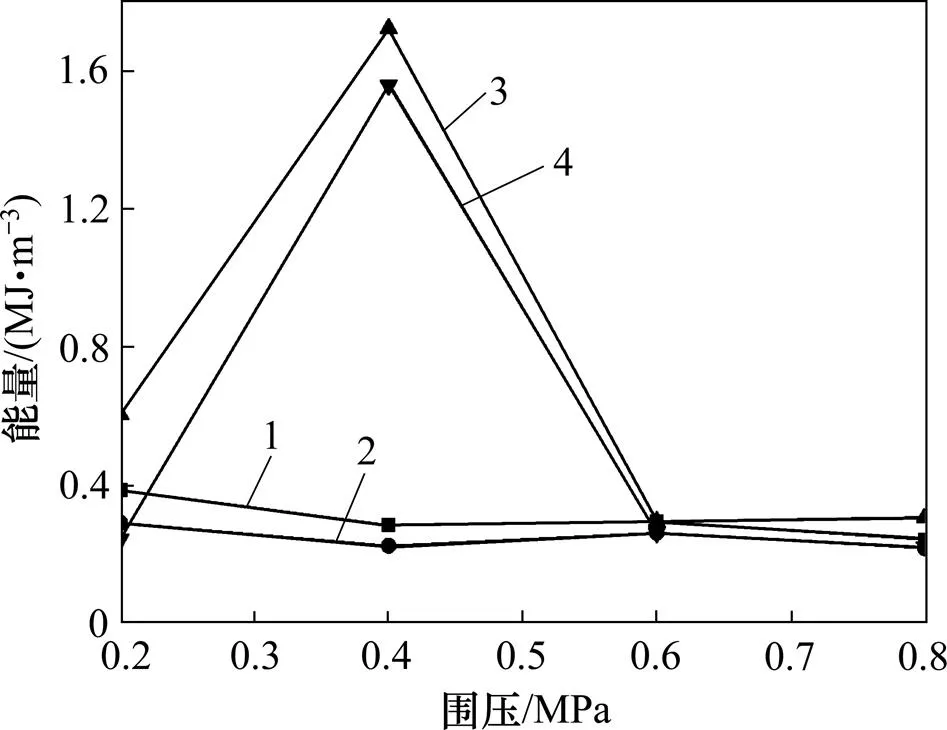
1—峰值点轴向能量−速率曲线；2—峰值点总能量−速率曲线；3—破坏点轴向能量−围压曲线；4—破坏点总能量−围压曲线。

由图9可知：总体来看，轴向能量−应变曲线与总能量−应变曲线在不同卸荷速率下没有发生明显的变化，不同于围压对能量−应变曲线的影响。

图10所示为不同卸荷速率的能量演化曲线。由图10可知：卸围压速率对应力−应变曲线有着较明显的影响，主要体现在卸荷点处与峰值点处。速率越大，卸荷点处应力−应变曲线的转折越明显，峰后变化越突然，峰值应力差也基本呈减小的趋势，具体值见表3。

卸荷/( MPa∙s−1)：(a) 0.2；(b) 0.4；(c) 0.8 1—应力−应变曲线；2—轴向能量−应变曲线；3—总能量−应变曲线。

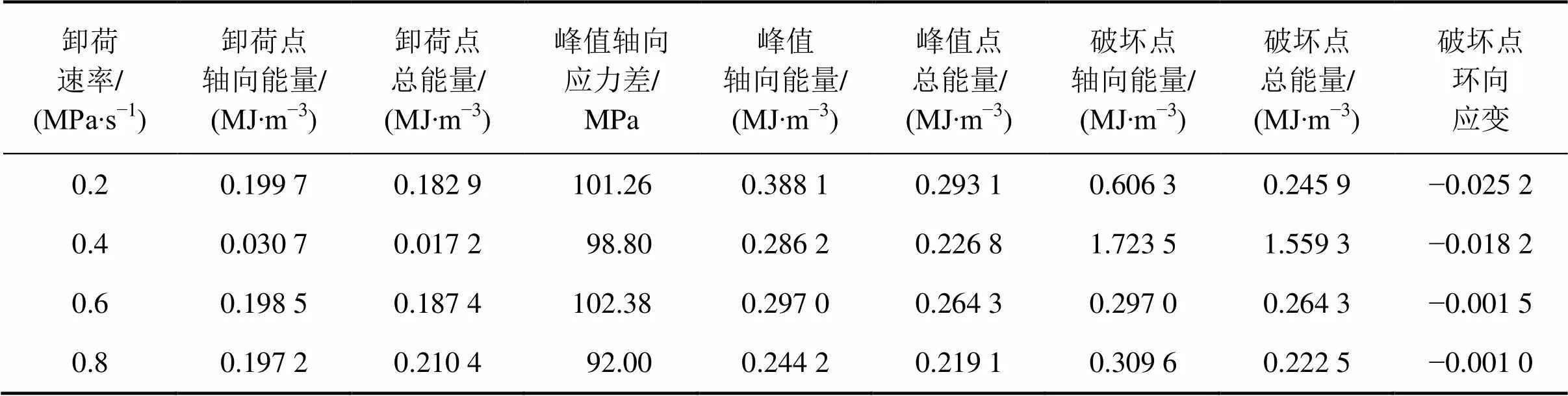
表3 卸载试验结果

从图10中的曲线2可以看出：卸荷速率越快，轴向能量在破坏点附近的拐点越明显，结合表3中的轴向能量具体值与图9中峰值点轴向能量−速率曲线可以看出：峰值处轴向能量随卸荷速率增加而逐渐减小，而卸荷速率对于破坏点轴向能量−速率曲线的影响并不是很明显。

卸荷速率增加，图10所示的总能量−应变曲线峰值处的总能量变化率越快。结合图9中的峰值点总能 量−速率曲线，峰值处总能量也随卸荷速率的增加而减小，而卸荷速率对图9中破坏点的总能量−速率曲线影响较小。但当卸荷速率为0.2 MPa/s时，破坏处轴向能量曲线与总能量曲线的能量差为0.852 2 MJ/m3，而当速率为0.8 MPa/s时，能量差已减小至0.087 1 MJ/m3，表明卸荷速率越快，岩样大部分能量都会用于释放，用于内部消耗的能量越少，这对现场开挖有着重要的指导意义。

5 不同路径能量的演化规律

在不同应力路径下，轴向能量−应变曲线对应应力−应变曲线破坏点处，都出现1个能量曲线增长速率的拐点，拐点的出现不受应力路径的影响。对于高围压下出现塑性流动的岩样，应力−应变曲线不能表述其破坏时，轴向能量−应变曲线可以作为一种很好的表述工具。

岩样实际吸收的总能量曲线在峰值处明显反向增大，在30 MPa时曲线转折较突然，在40 MPa时这种转折也变得平缓，并且总能量开始出现负值，表明岩样在峰后出现塑性应变时，还处于围压较高的环境，导致采用式(2)计算时岩样对液压作做负功较大，在曲线上表现为负向增大。尤明庆[12]采用此种计算方法时，路径相对简单，其对结果的影响不突出，但复杂路径下的能量计算不能作为定量分析的手段。

从初始卸荷围压、卸围压速率的能量演化规律来看，在破坏点之后，轴向能量与总能量的增大基本呈平行状态，这也表明岩样在破坏临界点前，岩样吸收能量用于内部消耗与能量释放，岩样被破坏后，即使吸收能量，也基本不用于岩样内耗。

张志镇等[8]提出了红砂岩的储能极限概念，并给出单轴加载条件下的储能极限约为0.25 MJ/m3。不同路径下对大理岩进行加、卸荷试验，从试验机对试样作功得到的轴向能量与试样实际吸收的总能量来看，应力路径变化，各阶段的能量都发生变化，一方面可能是由于岩样自身结构的影响，另一方面应力路径变化也改变了岩样不同阶段的受力状态，能量随之变化。

加轴压、卸围压试验在围压40 MPa时，卸荷点轴向能量为0.025 6 MJ/m3，峰值处的轴向能量为0.161 1 MJ/m3，破坏点处的轴向能量为0.949 0 MJ/m3，能量均低于10，20和30 MPa时对应特殊点的能量，此方案明显不同于其他方案，岩样自身性质的影响超过了围压的影响。

从岩样实际吸收的总能量变化曲线来看，卸荷速率的变化没有改变曲线的整体演化趋势，而随着围压的增大，总能量曲线由近轴向能量−应变曲线逐渐改变为近应力−应变曲线，其原因还有待进一步探究，并且由于试验条件限制，没有给出曲线变化对应的具体围压界限值，只是依据试验现有方案，粗略划分低围压(10 MPa和20 MPa)与高围压(30 MPa和40 MPa)。

6 结论

1) 不同应力路径下岩样破坏过程的轴向能量曲线经历了缓慢增大、快速增大、缓慢增大、释放的演化过程，作为非线性曲线，开始时增长速率较小，慢慢增大到极值后，增长速率趋于稳定。而总能量曲线经历了缓慢增大、快速增大、缓慢减小、释放等阶段，同样呈非线性增大，开始时增长速率较小，但慢慢增大到峰值后，逐渐减小至稳定。总能量变化曲线趋势与围压有关。

2) 不同路径下轴向能量曲线都存在1个变化率突然改变的拐点。而总能量−应变演化曲线的拐点出现在应力−应变曲线峰值对应处，卸荷速率越快，岩样实际吸收的总能量峰后负向增大越快。

3) 低围压(10 MPa和20 MPa)下加轴压、卸围压试验岩样的总能量演化规律与单轴加载试验结果相似，但单轴加载试样呈张拉破坏，而加轴压、卸围压试样仍呈剪切破坏。高围压下(30 MPa和40 MPa)加轴压、卸围压试验岩样的总能量演化规律与常规三轴试验结果相似。

4) 在不同破坏路径下，围压增大，轴向能量与总能量之间的能量差逐渐增大，岩样破坏消耗更多的能量，而卸围压速率增大，能量差却逐渐减小，岩样消耗的能量减小，更多的能量用于释放。

[1] 谢和平, 彭瑞东, 鞠杨. 岩石变形破坏过程中的能量耗散分析[J]. 岩石力学与工程学报, 2004, 23(21): 3565−3570. XIE Heping, PENG Ruidong, JU Yang. Energy dissipation of rock deformation and fracture[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 3565−3570.

[2] 王学滨. 基于能量原理的岩样单轴压缩剪切破坏失稳判据[J]. 工程力学, 2007, 24(1): 153−156. WANG Xuebin. Unstable criterion of rock specimen subjected to shear failure in uniaxial compression based on energy principle[J]. Engineering Mechanics, 2007, 24(1): 153−156.

[3] 高红, 郑颖人, 冯夏庭. 岩土材料能量屈服准则研究[J]. 岩石力学与工程学报, 2007, 26(12): 2437−2443. GAO Hong, ZHENG Yingren, FENG Xiating. Study on energy yield criterion of geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2437−2443.

[4] LI Q M. Strain energy density failure criterion[J]. International Journal of Solids & Structures, 2001, 38(38/39): 6997−7013.

[5] 陈卫忠, 吕森鹏, 郭小红, 等. 基于能量原理的卸围压试验与岩爆判据研究[J]. 岩石力学与工程学报, 2009, 28(8): 1530−1540. CHEN Weizhong, LÜ Senpeng, GUO Xiaohong, et al. Research on unloading confining pressure tests and rockburst criterion based on energy theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1530−1540.

[6] 刘建峰, 徐进, 李青松. 循环荷载下岩石阻尼参数测试的试验研究[J]. 岩石力学与工程学报, 2010, 29(5): 1036−1041. LIU Jianfeng, XU Jin, LI Qingsong, et al. Experimental research on damping parameters of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 1036−1041.

[7] 尤明庆, 华安增. 岩石试样破坏过程的能量分析[J]. 岩石力学与工程学报, 2002, 21(6): 778−781. YOU Mingqing, HUA Anzeng. Study on stability analysis and intelligent optimization for large underground caverns under high geostress condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 778−781.

[8] 张志镇, 高峰. 单轴压缩下红砂岩能量演化试验研究[J]. 岩石力学与工程学报, 2012, 31(5): 953−962. ZHANG Zhizhen, GAO Feng. Experimental research on energy evolution of red sandstone samples under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 953−962.

[9] 王云飞, 郑晓娟. 粗砂岩变形破坏过程中的能量演化机制[J]. 河南理工大学学报(自然科学版), 2015, 34(1): 30−34.WANG Yunfei, ZHENG Xiaojuan. Energy evolution mechanism in deformation and destruction process of grit stone[J]. Journal of Henan Polytechnic University(Natural science), 2015, 34(1): 30−34.

[10] 赵宝云, 郑颖人, 李子运, 等. 压缩作用下砂岩变形破坏过程中的能量特征[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(10): 1126−1131.ZHAO Baoyun, ZHENG Yingren, LI Ziyun, et al. Energy properties of sandstone in the process of deformation failure under compression condition[J]. Journal of Liaoning Technical University(Natural Science), 2016, 35(10): 1126−1131.

[11] 丛宇. 卸荷条件下岩石破坏宏细观机理与地下工程设计计算方法研究[D]. 青岛: 青岛理工大学土木工程学院, 2014: 57−60. CONG Yu. Study on rock macroscopic and mesoscopic failure mechanism under unloading conditions and designing and calculating methods of underground engineering[D]. Qingdao: Qingdao University of Technology. School of Civil Engineering, 2014: 57−60.

[12] 尤明庆. 岩石的力学性质[M]. 北京: 地质出版社, 2007: 175−177.YOU Mingqing. Mechanical properties of rock[M]. Beijing: Geology Publishing House, 2007: 175−177.

Energy evolution principle of fracture propagation of marble with different unloading stress paths

CONG Yu1, 2, WANG Zaiquan2, ZHENG Yingren3, FENG Xiating1, ZHANG Liming2

(1. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China; 2. School of Science, Qingdao Technological University, Qingdao266033, China; 3. Department of Civil Engineering, Logistical Engineering University, Chongqing 400041, China)

With the aim to explore the principles of real-time evolution of energy in the fracture propagation, the loading and unloading tests were carried out including the marble specimens with different stress paths for the analysis of evolution principles of axial energy and actual absorbed energy as the strain changes. The results show that the axial energy rises nonlinearly as the strain increases with the complex stress paths. The rate of rise remains low at the initial stage, and the rate will turn to an abrupt inflection point and tend to be stabilized when the rate grows gradually to the critical damage point. With different stress paths, the curves of axial energy−strain and gross energy−strain have abrupt inflection points of rate, and the point of the axial energy appears at the critical damage of corresponding stress−strain curves while the point of the gross energy appears at the corresponding peak. The change of confining pressure fails to change the axial energy of the specimen with different stress paths. However, with different confining pressures, the gross energy–strain curve of loading axial pressure and unloading confining pressure present different forms. The rate of the unloading confining pressure does not change the curve form of axial energy and gross energy, and it can only alter the changing rates of the curves at different stages. With different stress paths, the increase of confining stress comes with the increase of the gap between axial energy and gross energy while the effect on unloading rate is just on the contrary.

energy evolution; stress path; unloading confining pressure; inflection point

10.11817/j.issn.1672-7207.2016.09.031

TD315

A

1672−7207(2016)09−3140−08

2015−09−03；

2015−10−30

国家自然科学基金资助项目(41372298, 11232024, 41320104005, 41472270)；中国博士后科学基金资助项目(2015M5722232) (Projects(41372298, 11232024, 41320104005, 41472270) supported by the National Natural Science Foundation of China; Project(2015M5722232) supported by the China Postdoctoral Science Foundation)

丛宇，博士(后)，从事岩石力学及地下工程稳定性研究；E-mail: cuncin@163.com

(编辑 刘锦伟)