基于粗糙集理论的岩体结构面模糊C均值聚类分析

秦胜伍，陈骏骏，陈剑平，韩旭东，张文，翟健健，刘绪



基于粗糙集理论的岩体结构面模糊均值聚类分析

秦胜伍，陈骏骏，陈剑平，韩旭东，张文，翟健健，刘绪

(吉林大学建设工程学院，吉林长春，130026)

基于在利用模糊均值聚类算法对岩体结构面产状进行优势分组时，需要人为确定分组数和初始聚类中心，在迭代过程中容易陷入局部最优解的问题，通过改进聚类中心的算法，提出一种基于粗糙集的模糊均值聚类算法，以优化迭代过程，并通过对比多项聚类有效性检验参数，确定最优聚类分组情况。最后采用模糊均值聚类算法和改进后的算法对浙江白鹤隧道左洞测得的结构面产状进行优势分组并对比。计算结果表明，本文所提出的方法聚类效果明显优于模糊均值聚类算法。

结构面；粗糙集；优势分组；模糊均值聚类；聚类中心；有效性检验

岩体由结构面和结构体2个基本单元组成[1]，且岩体中结构面的存在和分布是造成岩体具有不连续性和各向异性等性质的主要原因，同时也是控制岩体工程稳定性的重要因素。在工程地质分析过程中，岩>体结构面产状的统计分析是极为重要的基础工作[2]。通过现场勘查获得结构面第一手资料后，要及时在室内进行统计分析，以便为工程设计提供参考。传统的方法主要是依靠绘制节理散点图、等密度图和玫瑰花图等比较直观的图形来判断分析结构面的分布规律，但此类方法不能准确确定其优势方位，而且这些方法是将走向、倾向、倾角分离出来进行分析，对岩体结构面的分析也比较粗糙[3]，且在结构面裂隙非常发育的地区很难得到准确结果。SHANLEY等[4]最早提出结构面产状的聚类算法，随后经过改进，发展了用于结构面识别的模糊均值聚类算法[5−6]，能在一定程度上较好地反映岩体结构面的分布情况，但由于该方法的聚类数和初始聚类中心通常依靠人为确定，在处理数据量较大的样本时，容易陷入局部最优解，造成结果不准确。针对模糊均值聚类算法存在的缺陷，许多学者提出了多种改进方法，如：蔡美峰等[7]提出用遗传算法来解决FCM算法计算时存在的局部最优问题；张奇等[8]提出基于凝聚层次分析法的模糊均值聚类算法，有效地克服了孤值点对聚类结果的影响；徐黎明等[9]提出基于混沌理论的FCM算法，解决了FCM算法对初始值敏感和局部最优解的问题；LI等[10]采用粒子群算法对FCM算法进行优化，使分类结果符合全局数据分布规律。本文在前人研究基础上，结合粗糙集理论，提出一种基于粗糙集理论的结构面产状优势分组的新方法。这种方法优化了聚类中心的计算过程，能有效避免在迭代计算过程中陷入局部最优解，使分类结果符合整体结构面产状分布规律。最后，通过对浙江诸永高速白鹤隧道左洞K127+001处测得的结构面产状进行实例分析，验证该方法的可行性和可靠性。

1 结构面的空间表示方法

在对岩体结构面进行优势分组时，通常将结构面的产状作为划分依据。结构面的产状一般用倾向(0°≤＜360°)和倾角(0°≤≤90° )来表示。假设岩体结构面为一空间平面，则其产状可用结构面单位法向量来表示，建立如图1所示空间直角坐标系，结构面产状单位法向量坐标与倾向()、倾角()的关系 为[11−13]

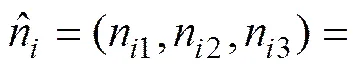
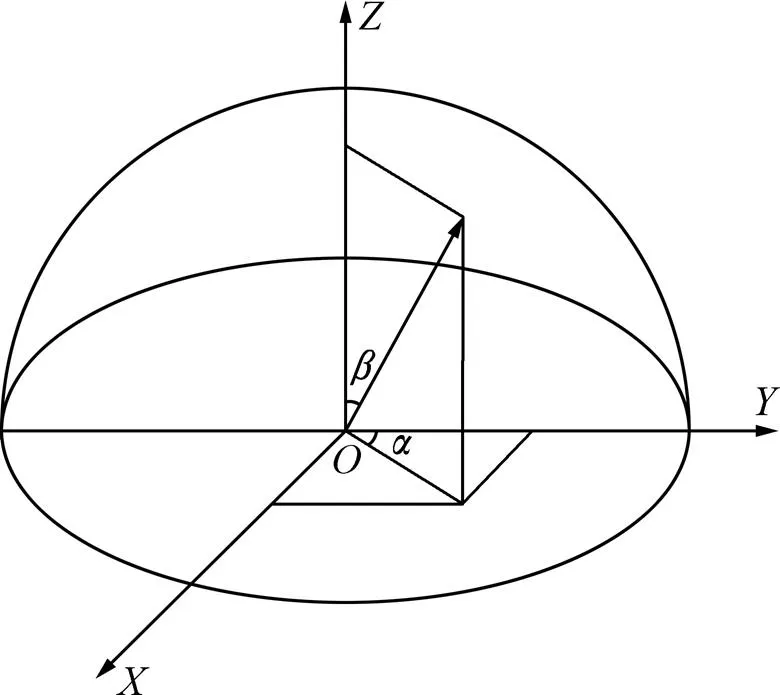
图1 结构面的空间坐标表示

2 基于粗糙集的模糊均值聚类算法的理论基础

2.1 粗糙集理论

在粗糙集理论中，为非空有限集合，称为论域；是定义在上的等价关系；用表示的所有等价类的类簇(集合)；用[]表示在等价关系下包含元素(∈)的等价类；对于论域的任意子集，有下近似集和上近似集分别满足：

根据式(2)和式(3)中的集合关系式可知：下近似集表示的是某对象一定属于类；而上近似集表示某对象可能属于类。在岩体结构面产状优势分组计算中，可以采用粗糙集理论中的上近似集和下近似集来解决相邻2个分组边界数据的归属。具体的上近似集和下近似集可以利用关系矩阵和基本的矩阵运算求得[14]。

2.2 模糊均值聚类算法聚类中心的改进

在经典均值聚类分析中，聚类中心通常依靠人为确定。在本文中，若结构面产状的分类边界比较明显，则可以将每个类簇的空间中心点作为聚类中心，具体可通过求解每一类中所有结构面产状数据点的算数平均坐标值求得。

设研究区的结构面产状可以分为组，A:(=1，2，…，)表示第组中的所有结构面产状集合，x(=1，2，…，n)表示第类中的某一结构面产状，则第类的聚类中心V可以表示为

但是上述方法在处理分组边界不清晰的问题时，很难得到准确的结果，LINGRAS[15]通过利用粗糙集中的上近似集和下近似集的对均值聚类算法的聚类中心算法进行改进，可得到基于粗糙集的均值聚类算法聚类中心：

在式(5)基础上，结合模糊集理论，可得到基于粗糙集的模糊均值聚类算法的聚类中心[16]：

式中：u为样本x属于类别的隶属度关系。根据KIM等[17]提出的 KH 算法，定义隶属度的函数为目标 函数：

式(6)和式(7)中，隶属度u满足：

当X≠V时，隶属度u可以表示为

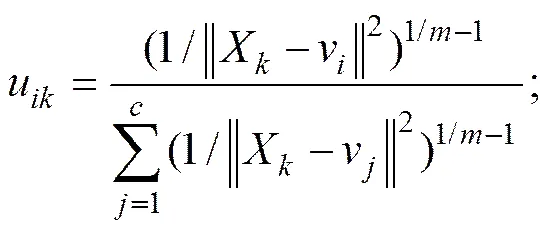
=1，2，…，；=1，2，…，(9)

式中：为控制着隶属度分配和聚类模糊程度的加权参数，其最佳取值范围为[1.5，2.5]，在一般情况下，取2.0[6−7,18]。

利用式(7)所示目标函数进行迭代优化可以使其收敛到1个极小值，即可得到最优分类，且在计算过程中通过聚类中心的优化可以避免陷入局部最优解，得到更具有全局意义的结果。

2.3 聚类有效性检验和最优聚类数的确定

在模糊均值聚类算法中，聚类数的取值是影响聚类结果的1个重要因素，通常根据情况人为划分确定。为了得到合理的聚类结果，本文首先通过观察结构面产状的极点图及密度等值线图，大体估计可能出现的分类组数，对这些可能出现的分类组数分别进行聚类计算得出相应结果，再利用聚类结果有效性检验函数对聚类结果进行最优化筛选。为了避免单一性，采用Xie−Beni指标XB、分类熵指标m和模糊分类系数m检验行聚类效果，计算式为[7, 16]：

式中：为聚类分组数；为样本总数；u为隶属度。2(X,V)为某一结构面样本到聚类中心V的距离的平方；为距离最近的2个聚类中心之间的距离的平方；对数底数＞0，且规定当u=0时，，本文取自然对数。当计算所得的指标S越小，分类熵指标H越接近于0，模糊分类系数F越接近1时，聚类效果越好；反之，聚类效果越差。综合运用上述3个聚类有效性检验方法，确定合理的聚类数即为结构面分组数。

3 实现过程

基于粗糙集的模糊均值聚类算法实现过程见图3，具体步骤如下。

1) 数据预处理。将野外实测获得的结构面产状用结构面单位法向量的形式来表示，且设定进行聚类的对象数即结构面总数为，对象中的元素可以用三维空间中的有限集来表示。其中X为第个空间结构面法向量对应的坐标，且X= (cosαsinβ，sinαsinβ，cosβ)(=1，2，…，)。

2) 聚类数范围的确定。通过观察研究区内结构面产状的极点图和等密度图，确定聚类数的取值范围。

3) 基于粗糙集的模糊均值聚类计算。利用改进后的算法对研究区聚类数取值范围内的值分别进行计算。

4) 确定最优聚类结果。利用聚类有效性检验方法对步骤3)中所得的结果进行对比分析，并综合考虑实际因素确定最优聚类结果。

4 实例分析

为了验证基于粗糙集的模糊均值聚类算法在结构面优势分组时的可靠性，取浙江诸永高速白鹤隧道左洞K127+001处测得的472个节理裂隙产状(倾向、倾角)进行聚类分析。白鹤隧道位于浙江省诸永高速台州段，该地区为侵蚀剥蚀中山、中低山丘陵区，处于余姚—丽水大断裂与鹤溪—奉化大断裂之间的断块内。研究区隧道洞身围岩分布有含黏性土碎石及强风化灰黄色、紫红色晶屑凝灰岩，岩石裂隙较发育。地下水基本为基岩裂隙水。复杂的地质构造使隧道在施工过程中常发生塌方和涌水的现象，对人们的生命财产安全造成威胁，因此，正确认识隧道区结构面的分布情况具有重要的工程指导意义。

根据在白鹤隧道现场勘查测定的472组结构面产状，采用赤平极射投影法可得到结构面产状的极点图及等密度等值线图，如图2所示。

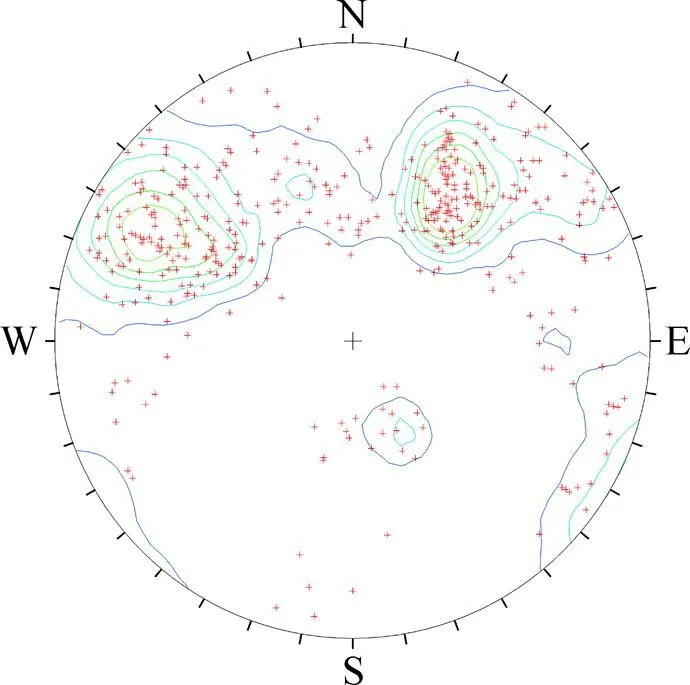
图2 结构面产状极点图及密度等值线图

从图4可以确定研究区结构面的聚类数为2~5。现采用模糊均值聚类算法和基于粗糙集的模糊均值聚类算法对研究区测得的结构面产状进行聚类计算，得到的聚类结果见图3~6。

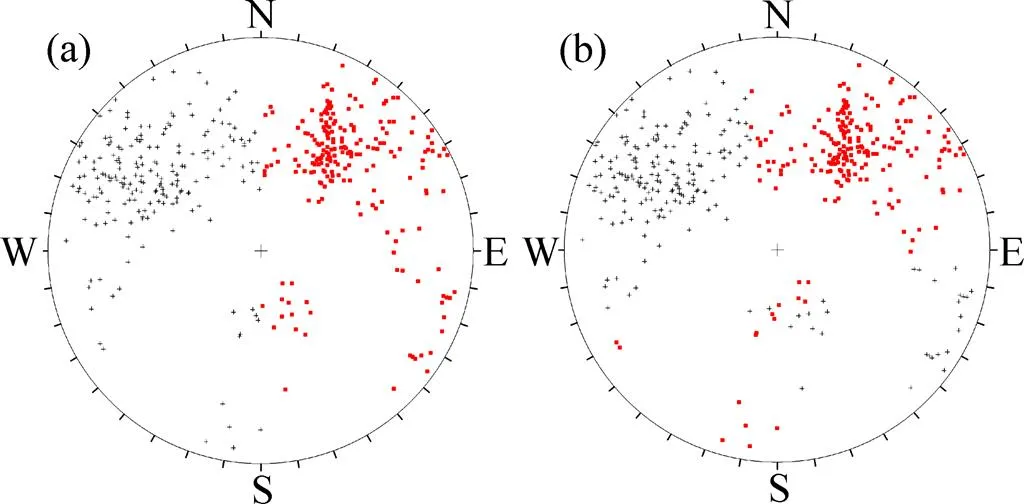
(a) 模糊C均值聚类算法；(b) 基于粗糙集的模糊C均值聚类算法

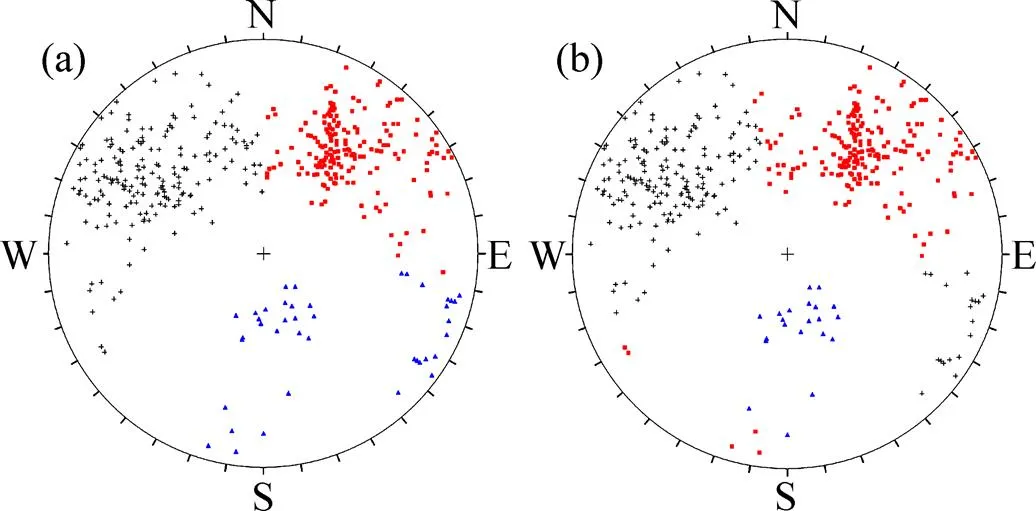
(a) 模糊C均值聚类算法；(b) 基于粗糙集的模糊C均值聚类算法

(a) 模糊C均值聚类算法；(b) 基于粗糙集的模糊C均值聚类算法

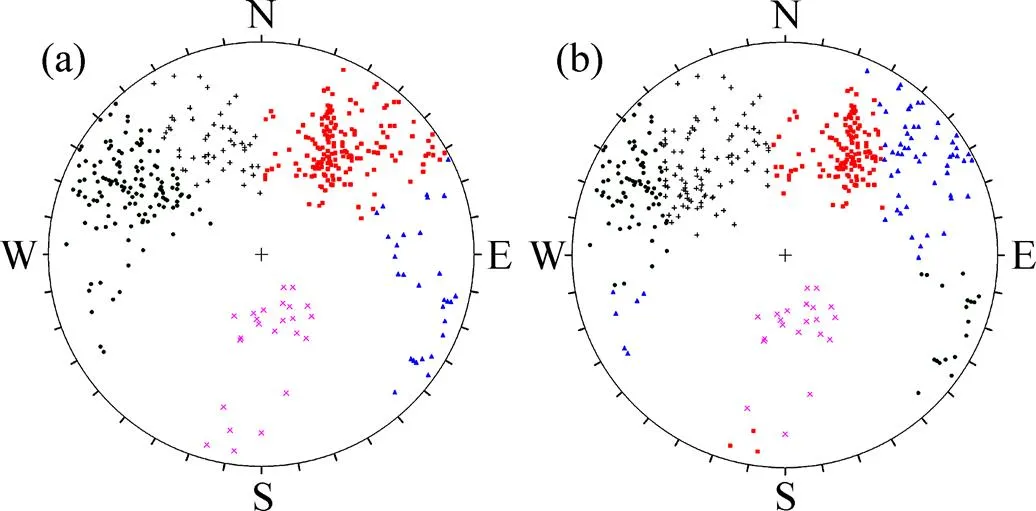
(a) 模糊C均值聚类算法；(b) 基于粗糙集的模糊C均值聚类算法

为了比较2种方法得到的评价结果，本文通过计算得到2种方法在不同分组情况下的聚类有效性检验指标，如表1和表2所示。对比分析表1和表2中的各校指标可知：

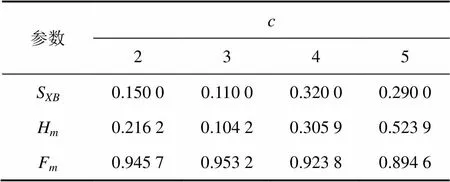
表1 模糊C均值聚类算法聚类有效性检验指标

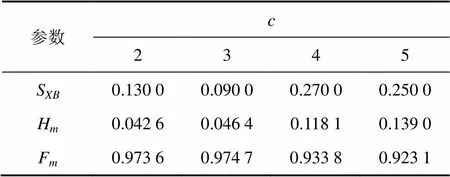
表2 基于粗糙集的模糊C均值聚类算法聚类有效性检验指标

当分别为2，3，4和5时，由模糊均值聚类算法所得XB和m均比本文方法的大；m均比本文方法的小。根据2.3节中3个评价指标针对聚类有效性检验的判别标准(XB越小越优，m越接近0越优，m越接近1越优)可知：本文提出的基于粗糙集的模糊均值聚类算法得到的分类结果优于传统模糊均值聚类算法的分类结果。

进一步分析基于粗糙集的模糊均值聚类算法得到的结果(表2)可知：除m外，其余2项指标均表明聚类数为3时的聚类效果最佳。实际上，当聚类数为3时的m与为2时的m几乎相等，因此，可以确定聚类数为3时的聚类结果是最佳的。

综上所述，本文中改进后的基于粗糙集的模糊均值聚类算法优于原有的模糊均值聚类算法，并且可得到白鹤隧道左洞的结构面优势分组情况，如图7及表3所示。

图7 白鹤隧道结构面优势分组结果

表3 白鹤隧道左洞岩体结构面聚类结果

5 结论

1) 基于粗糙集的模糊均值聚类算法的聚类效果明显优于模糊均值聚类算法，本文提出的方法具有更好的有效性和实用性。

2) 基于粗糙集的模糊均值聚类算法在计算过程中可以根据数据分布自动搜索聚类中心，避免了因为人为确定初始聚类中心不准确而造成的误差，使迭代结果更具有全局意义。

3) 应用本文的新方法对浙江白鹤隧道左洞岩体结构面进行了有效的优势分组分析，得到了可靠的优势分组结果，可为后续研究提供参考。

[1] 徐光黎, 潘别桐. 岩体结构模型与应用[M]. 武汉: 中国地质大学出版社, 1993: 1−5. XU Guangli, PAN Biedong. Modelling of rock mass structures and its applications[M]. Wuhan: China University of Geosciences Press, 1993: 1−5.

[2] 冯羽, 马凤山, 巩城城, 等. 节理岩体结构面优势产状确定方法研究[J]. 工程地质学报, 2011, 19(6): 887−892. FENG Yu, MA Fengshan, GONG Chengcheng, et al. Data analysis method for optimized and dominant orientations of joints in rock mass[J]. Journal of Engineering Geology, 2011, 19(6): 887−892.

[3] 周玉新, 周志芳, 孙其国. 岩体结构面产状的综合模糊聚类分析[J]. 岩石力学与工程学报, 2005, 24(13): 2283−2287. ZHOU Yuxin, ZHOU Zhifang, SUN Qiguo. Synthetical fuzzy clustering analysis for joints occurrence of rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2283−2287.

[4] SHANLEY R J, MAHTAB M A. Delineation and analysis of clusters in orientation data[J]. J Math Geol, 1976, 8(3): 9−23

[5] MAHTAB M A, YEGULALP T M. A rejection criterion for definition of clusters in orientation data[C]//Issues in Rock Mechanics, Proceedings of the 22nd Symposium on Rock Mechanics. New York: American Institute of Mining Metallurgy and Petroleum Engineers, 1982: 116−123.

[6] HAMMAH R E, CURRAN J H. Fuzzy cluster algorithm for the automatic identification of joint sets[J]. Int J Rock Mech Min Sci, 1998, 35(7): 889−905.

[7] 蔡美峰, 王鹏, 赵奎, 等. 基于遗传算法的岩体结构面的模糊均值聚类方法[J]. 岩石力学与工程学报, 2005, 24(3): 371−376. CAI Meifeng, WANG Peng, ZHAO Kui, et al. Fuzzy-means cluster analysis based on genetic algorithm for automatic identification of joint sets[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(3): 371−376.

[8] 张奇, 王清, 阙金声, 等. 基于凝聚层次聚类分析法的岩体随机结构面产状优势分组[J]. 岩土工程学报, 2014, 36(8): 1432−1437. ZHANG Qi, WANG Qing, QUE Jinsheng, et al. Dominant partitioning of discontinuities of rock masses based on AGNES[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1432−1437.

[9] XU Liming, CHEN Jianping, WANG Qing, et al. Fuzzy-means cluster analysis based on mutative scale chaos optimization algorithm for the grouping of discontinuity sets[J]. Rock Mechanics and Rock Engineering, 2013, 46(1): 189−198。

[10] LI Yanyan, WANG Qing, CHEN Jianping, et al. K-means algorithm based on particle swarm optimization for the identification of rock discontinuity sets[J]. Rock Mechanics and Rock Engineering, 2015, 48(1): 375−385.

[11] 秦胜伍. 基于GIS的隧道施工超前地质预报[D]. 长春: 吉林大学建设工程学院, 2009: 64−69. QIN Shengwu. Geological prediction ahead of working face during tunnel construction based on GIS[D]. Changchun: Jilin University. College of Construction Engineering, 2009: 64−69.

[12] 陈剑平, 石丙飞, 王清. 工程岩体随机结构面优势方向的表示法初探[J]. 岩石力学与工程学报, 2005, 24(2): 241−245. CHEN Jianping, SHI Bingfei, WANG Qing. Study on the dominant orientations of random fractures of fractured rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 241−245.

[13] 范雷, 王亮清, 唐辉明. 节理岩体结构面产状的动态聚类分析[J]. 岩土力学, 2007, 28(11): 2405−2408. FAN Lei, WANG Liangqing, TANG Huiming. Dynamic cluster analysis of discontinuity orientations of jointed rock mass[J]. Rock and Soil Mechanics, 2007, 28(11): 2405−2408.

[14] 刘财辉, 苗夺谦. 基于矩阵的粗糙集上、下近似求解算法[J]. 计算机应用研究, 2011, 28(5): 1628−1630. LIU Caihui, MIAO Duoqian. Algorithm of upper and lower approximations based on matrix[J]. Application Research of Computers, 2011, 28(5): 1628−1630.

[15] LINGRAS P. Interval set clustering of web users with Yough k-means[J]. Journal of Intelligent Information System, 2004, 23(1): 5−16.

[16] BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press, 1981: 203−239.

[17] KIM D W, LEE K H, LEE D. Fuzzy clustering of categorical data using fuzzy centroids[J]. Pattern Recognition Letters, 2004, 25(11): 1263−1271.

[18] 高新波, 李洁, 谢维信. 模糊均值聚类算法中参数的优选[J]. 模式识别与人工智能, 2000, 13(1): 7−11. GAO Xinbo, LI Jie, XIE Weixin. Optimal choice of weighting exponent in a fuzzy-means clustering algorithm[J]. Pattern Recognition and Artificial Intelligence, 2000, 13(1): 7−11.

Fuzzy-means cluster analysis based on rough set for grouping of discontinuities

QIN Shengwu, CHEN Junjun, CHEN Jianping, HAN Xudong, ZHANG Wen, ZHAI Jianjian, LIU Xu

(College of Construction Engineering, Jilin University, Changchun 130026, China)

When using the fuzzy-means method to analysis the distribution of discontinuities in the discontinuities distribution research in rock mass, the number of group and cluster centers should be firstly determined, which might fall into the locally optimal solution during calculation, in order to solve the problem, a new method was proposed by the optimization algorithm of cluster centers for the dominant partitioning of discontinuities of rock mass based on rough set. This method optimizes the iterative process and can get significant results. Numbers of clustering validity test parameters were taken as laboratory test index to determine the best result of dominant partitioning. Finally, taking the data of discontinuities which were measured in the left tunnel of Baihe in Zhuyong Highway, Zhejiang Province, as an example, the new method and fuzzy-means cluster was used to analysis and calculate the possible situation. The results show that the proposed method is obviously better than the fuzzymeans method.

discontinuity; rough set; dominant partitioning; fuzzy-means cluster analysis; cluster centers; effectiveness test

10.11817/j.issn.1672-7207.2016.09.029

P642.3

A

1672−7207(2016)09−3125−06

2015−08−16；

2015−10−22

国家自然科学基金青年基金资助项目(41202197)；国家自然科学基金重点资助项目(41330636)；中国博士后科学基金资助项目(20100471265)；国土资源部公益性行业科研专项(201211095-6)；科技部国家重大仪器科学设备开发专项项目(2011YQ030133)(Project(41202197) supported by the National Natural Science Foundation of China for the Youths; Project (41330636) supported by the National Natural Science Foundation of China; Project (20100471265) supported by the Postdoctoral Science Foundation of China; Project(201211095-6) supported by the Ministry of Land and Resources for Public Welfare Industry Special Research; Project(2011YQ030133) supported by Ministry of Science and Technology for Major Scientific Instruments and Equipment Development)

秦胜伍，博士，副教授，从事工程地质灾害研究；E-mail：qinsw@jlu.edu.cn

(编辑 陈灿华)