一种基于分形的RDX感度计算方法
2016-10-13胡钟元欧阳的华付凯城
胡钟元,欧阳的华,付凯城,赵 雁
一种基于分形的RDX感度计算方法
胡钟元,欧阳的华,付凯城,赵 雁
(武警工程大学,陕西 西安,710086)
RDX表面粗糙度进行了定量分析,并将感度的试验测试结果与表面分维数进行了对比。结果表明,分形维数越大,其表面越粗糙, RDX的感度在一定程度上随着其表面分维数的增大而增大。
RDX;分形维数;撞击感度;摩擦感度
分形是法国数学家芒德勃罗创造出来的一种新的科学观和方法论。其定义为非整数维形式充填空间的形态特征。它以自然界中无规则的复杂的无序系统为研究对象,用分形维数来表征其复杂程度,弥补了传统欧式几何的空白。
目前,分形理论在材料领域已经得到了应用。杨峰等人研究了页岩纳米孔隙的分形特征[1];王唯威运用分形理论建立了多孔介质分形结构模型,来描述多孔介质内的导热和流动问题[2];王毅研究了炸药粒度的热点效应,通过分形维数来表示它的热点,进而表示感度[3];宋小兰等人结合分形理论,建立热感度模型来研究HMX的机械感度[4]。通过各种分形计算软件,可以将一些复杂的不规则的物体表面通过分形维数定量地去描述,这是引入分形理论后的一种理论提升。
炸药感度是定义炸药起爆难易度的物理量,是炸药安全性和作用可靠性的关键标度。炸药的安全性研究一直是国内火炸药研究的重要课题之一。研究炸药感度的方法很多,刘玉存等通过炸药颗粒的粒度来研究炸药机械感度[5];张琳通过分子结构特征来研究炸药感度[6];J.K.Dienes等通过热点学说来解释感度[7]。但对于感度的研究大多是定性地去描述,而本文则是基于分形理论,运用Matlab中的Fraclab分形计算软件,通过微观SEM图像定量地计算出两类RDX基炸药微粒的表面分维,通过对比其粒径、表面粗糙程度,最后得出其在宏观上体现出的各个性质。对于含能材料等相关性质的研究具有重要的意义。
1 盒维数模型和表面分维
盒维数(Box Dimension)是应用最广泛的维数之一,其基本思想是用一系列尺度相同的盒子(尺寸为)去覆盖对象,如覆盖某一个集合。用这些盒子把对象全部覆盖完,当尺寸趋于零时,盒子的个数的对数ln与尺寸倒数对数ln1/之比,就称为盒维数。故盒维数也可称为盒子个数增加的对数速率。数学模型如下:
设是R上的任意非空的有界子集;N是直径为,可以覆盖的集的最少个数,则盒维数可以定义为:
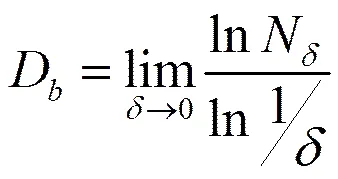
根据分形理论表面分维的定义,表面分维D的取值范围为2<D<3,而盒维数的取值范围为1<D<2,则可近似地认为D=D+1。
本文通过宽粒度和窄粒度RDX的SEM图片,运用灰度处理、图像二值化手段将其简化,通过Fraclab软件对它的盒维数进行计算,最终得出表面分维[8]。
2 分形计算软件Fraclab
2.1 Fraclab软件的检验
Fraclab软件是基于Matlab的一个计算分形维数软件。它通过编程,建立了自己的分维模型数据库,只需调用其中的模型就能完成相应的计算。本文通过Fraclab的盒维数计算模版,对相应的SEM扫描电镜图片进行计算,得出其盒维数。
在此,使用Kock雪花曲线对该软件的精确度进行检验。Kock雪花曲线是一个标准的分形曲线,该曲线是假设一个边长为1的等边三角形,取每边中间的1/3,接上去一个形状完全相似的但边长为其1/3的三角形,结果是一个六角形,现取六角形的每个边做同样的变换,即在中间三分之一接上更小的三角形,以此重复,直至无穷。外界变得越来越细微曲折,形状接近理想化的雪花,是一个完全自相似的图形,这就是Kock曲线,如图1所示。其分形维数为ln4/ln3 =1.26。
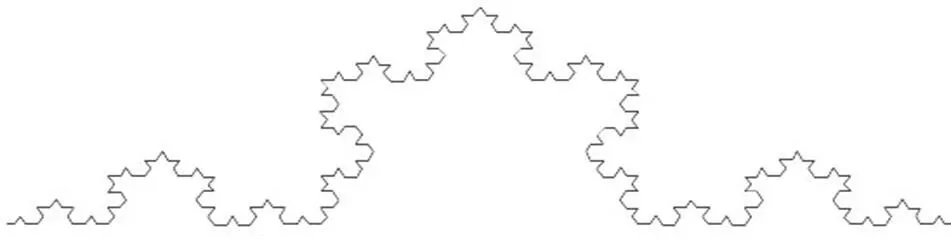
图1 Kock雪花曲线
使用Fraclab软件,载人Kock雪花曲线,再使用其中的盒维数计算功能进行计算,得到曲线,如图2所示。图2中,Kock曲线的盒维数为曲线斜率为1.37,更正系数为1,最大误差为5.2e-0.14%,和理论值的相对误差为8%。实验证明,Matlab环境下的Fraclab软件对于分形图形维数的计算是比较准确可靠的。
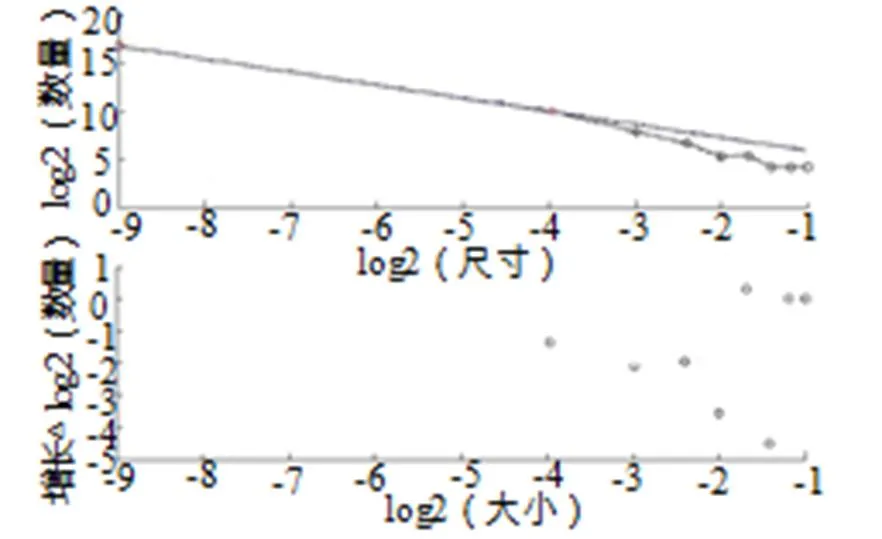
图2 Kock雪花曲线分形拟合曲线
2.2 Fraclab软件对宽粒度和窄粒度RDX基炸药的计算
本次计算采用筛分法制备宽粒度分布RDX样品,溶剂(丙酮)/非溶剂(去离子水)法制备窄粒度分布RDX样品,通过对两者的SEM灰度图片(图3)二值化,而后载入Fraclab软件进行分析处理。

(a) 宽粒度RDX (b) 窄粒度RDX
