A Class of Ruin Probability Model with Dependent Structure

Wang De-hui，Gao Jia-xing，Xu Zi-li，Xu Jin-jing and Zhang Xu-li

(School of Mathematics，Jilin University，Changchun，130012)



A Class of Ruin Probability Model with Dependent Structure

Wang De-hui，Gao Jia-xing，Xu Zi-li，Xu Jin-jing and Zhang Xu-li*

(School of Mathematics，Jilin University，Changchun，130012)

In this paper，we study a class of ruin problems，in which premiums and claims are dependent.Under the assumption that premium income is a stochastic process，we raise the model that premiums and claims are dependent，give its numerical characteristics and the ruin probability of the individual risk model in the surplus process.In addition，we promote the number of insurance policies to a Poisson process with parameter λ，using martingale methods to obtain the upper bound of the ultimate ruin probability.

ruin probability，dependent structure，individual risk model，Poisson process

2010 MR subject classification:91B30

Document code:A

Article ID:1674-5647(2016)03-0241-08

1　Introduction

The financial risk theory is a common research direction in mathematics，and theories related to ruin probability are the core contents.More and more researchers are getting interested in the theoretical foundation of ruin theory；moreover，they apply them to all aspects of the social economy.In reality，every insurance company must consider the corresponding ruin probability when radicating pricing strategies.Therefore，it is important to study the relationships between premium and claim income.Lundberg[1]and Cramer[2]put forward and perfected the well-known classical ruin model.However，the classical compound-Poisson risk modelis ideal，for it requires that the point process{N(t)，t≥0} is a Poisson process，and the cost of claims{Yi，i∈N+}is a sequence of independent and identically distributed variables with finite mean，independent of{N(t)，t≥0}and therate of premiums income per unit time is a constant(see[3]).As a result，some scholars made improvements，and they think the point process of insurance policies should not be a Poisson process.For example，Mao[4]introduced a generalized Poisson-geometric process with two parameters of claim numbers.Gerber[5]introduced a mixed Poisson risk process. Shiu[6]established a discrete-time model，where the number of claims process is assumed to be binomial.Grandell[7]discussed the ruin probability when the point process is a common or balanced renewal process.In the case of heavy-tailed claims，Kluppelberg and Mikosch[8]gave large deviations of ruin probability when the point process is a renewal process.Moreover，there exist dependence between claims，between interclaim times，and between claims and interclaim times.Asmussen and Albrecher[9]pointed out a causal dependence may be needed in practice，where for instance the size of a claim determines the distribution of the next interclaim times.When both claim sizes and interarrival times follows a certain dependent structure，Wang et al.[10]calculated the expression for the finite time ruin probability of a nonstandard risk model with a constant interest rate.Ambagaspitiya[11]also talked about the dependent structure between claim sizes and claim occurrence times.Albrecher and Boxma[12]considered the situation that the distribution of the time between two claim occurrences depends on the previous claim size.Zhang[13]proposed a dependent model between different insurance categories.And yet for all that，all of them ignored the dependent structure between premiums and claims.In order to be precise and compensate for financial mathematics theory(see[14]–[15])，in this paper，we raise a ruin model where premiums and claims are dependent based on the premium income being a stochastic process

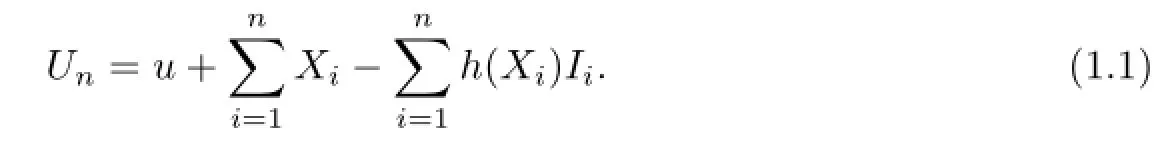
We focus on calculating the numerical characteristics of the surplus process when the claim income is a monotonous increasing function of the premium income，and use martingale methods to obtain the upper bound of the probability of the ultimate ruin.We begin by a specific example of Ping An Property and Casualty Insurance Company of China and then raise our model，giving its numerical characteristics and calculating its ruin probability approximately.Finally，we generalize the number of insurance policies to a Poisson counting process with parameter λ and give its upper bound of the ruin probability.

2　The Ruin Model with Dependent Structure Proposed

According to annual integrated accident insurance，which was promoted by Ping An Property and Casualty Insurance Company of China in 2014，claims of accidental death can be categorized into the following sorts(see Table 2.1).

Table 2.1Relationship between claims and insured amounts

In this kind of insurance，a policy holder’s claim is proportionate to his insured amount. Moreover，a policy holder can also choose other insurances like hospitalization insurance for accident，subsidy for delayed work and so on.The relationships between the claim and insured amount of these insurances are shown in the following forms(Tables 2.2 and 2.3) and the situation is when claims are less than 50 000 yuan.

Table 2.2Relationship between hospitalization insurance for accidents and insured amounts

Table 2.3Relationship between subsidies for delayed work and insured amounts

From the statistics，we find that the insured amount will grow linearly when the claim grows.However，this kind of insurance is not attractive enough in terms of the market.In Table 2.1，if a policy holder adds 46.5 to his current insured amount，he will get just 50 000 yuan which is fixed on value.In this case，people ignore the factor that they should get nonlinearly increasing claims when they pay more money on their insurance amount，which has a great effect on promoting consumptions.Enlightened from this，we want to figure out the relationships between claims and insured amount，building the corresponding ruin model.

On the basis of the classical risk model，we post an individual risk model，which focuses on the random premium income and dependent structure between the premiums and claims

where Unis the total surplus during a period，u is the initial surplus of a company，Xi，i=1，2，···，n，are independent and identically distributed random variables，h(Xi)is a random variable with respect to Xi，Ii(i=1，2，···，n)are claim times of the ith insurance policy，n is the total amount of policies in the time interval.When a policy holder buys a kind of insurance and meet with the corresponding accident during the insurance period，he will ask the insurer for claims，and the insurer will pay him matching compensation written on their contrast.For the ith insurance policy of this kind of insurance，the compensation will either occur or not.Suppose that Xiis the premium of ith insurance policy，then Xi(i=1，2，···，n)is a nonnegative random variable，and the corresponding claim is h(Xi). Therefore，the total surplus of the insurance during the period is equation(2.1).

3　Properties of the Model

3.1Numerical Characteristic

In this subsection，we discuss some properties of model(2.1).

Let Iibe the number of claims of the ith policy.To simplify the process，we require that a policy meets at most one claim.Ii=1 means the policy meets a claim，and Ii=0 means no claim.That is to say，Iiobeys 0-1 distribution，denoted as

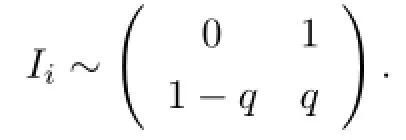
Let h(Xi)be the amount of the claims of ith policy when an accident happens.For simplicity，we require that whether a policy meets a claim or not are independent of the amount of the claims.Namely，Iiand h(Xi)are independent.

Denote

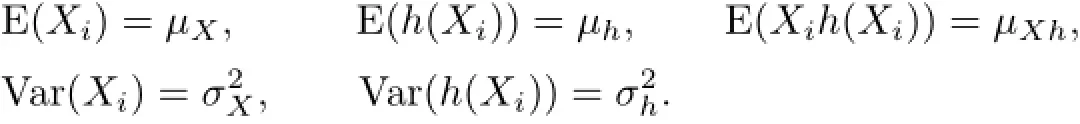
Under the above assumptions and conditions，we can easily compute the expectation of Un

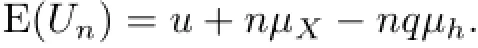
According to the law of total variance，we can compute the variance of Un

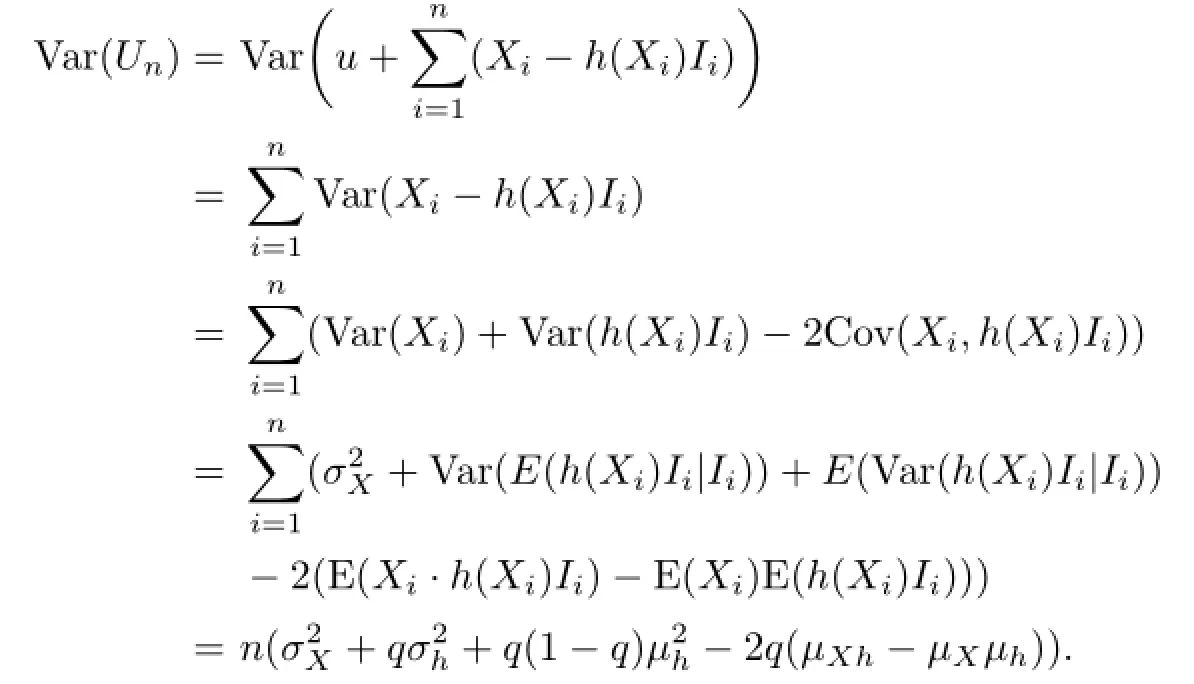
Also，by using the definition，we can get the generating function of Un

3.2Normal Approximation of Ruin Probability

On the base of the moment，we can now consider a normal approximation of ruin probability. When n is sufficiently large，we can use the central limit theory to normally approximate the process of the total surplus.Let Φ(x)represents the cumulative distribution function of standard normal distribution.We approximate the ruin probability by the following steps:

First，we utilize the distribution of the individual claim to figure out the mean value and variance of Un.

Secondly，we standardize the distribution of Un

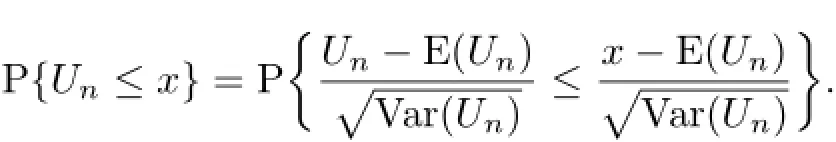
Thirdly，we use central limit theory to calculate the ruin probability

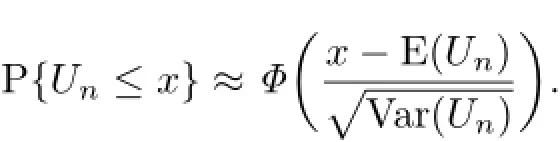
4　Extension of the Ruin Model

4.1Introduction to the New Model

In order to study the surplus process of an insurance company，we always have to study a long-term collective risk model.We extend our ruin model to long-term collective risk model by making the number of insurance policies be a Poisson counting process with parameter λ.Under the assumption，the surplus at t time is

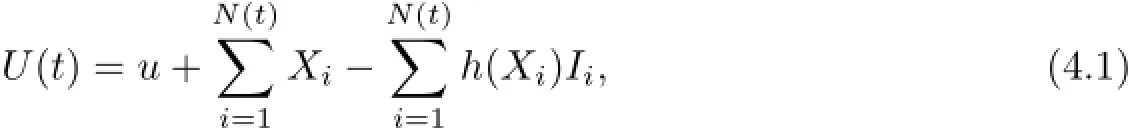
where u(≥0)is the initial surplus，N(t)is a Poisson counting process with parameter λ and it represents the number of insurance policies，is the total premium income until t time，(Xi)Iiis the total claims until t time.

4.2Some Properties of the New Model

Let

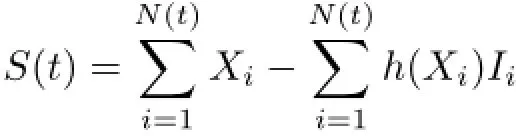
be the cumulative earnings until the time t.In order to run properly，we always require the expectation value for S(t)to be positive，that is，

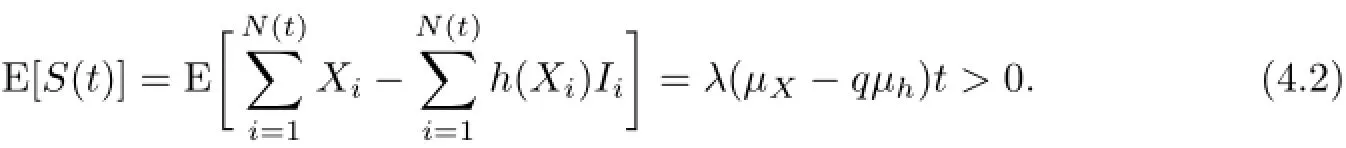
Namely，µX-qµh＞0.From this，we give the following definition.

Definition 4.1Denote E(Xi)=µX，E(h(Xi))=µh，q=P{Ii=1}，where Iihas a Bernoulli distribution.Based on the assumption thatµX-qµh＞0，we define safe load factor

Definition 4.2U(t)is the total surplus during the time[0，t].Define ruin time T=

Definition 4.3U(t)is the total surplus during the time[0，t]，T is ruin time.Define ultimate ruin probability Ψ(u)=P{T＜∞|U(0)=u}.

For the surplus process{S(t)，t＞0}，we can easily get

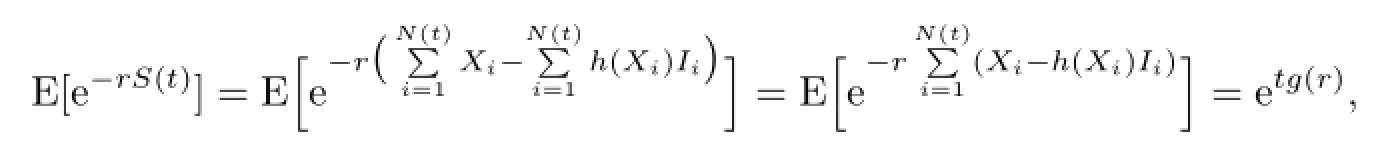
Remark 4.1Because Xi-h(Xi)Ii，i=1，2，3，···are independent and identically distributed，we let their collective cumulative distribution function be F(y)，and the above conclusion can be attained by using conditional expectation.For convenience，we assume that the second order moment of orgin for the random variables Xi-h(Xi)Ii，i=1，2，3，··· always exist.

Proof.For

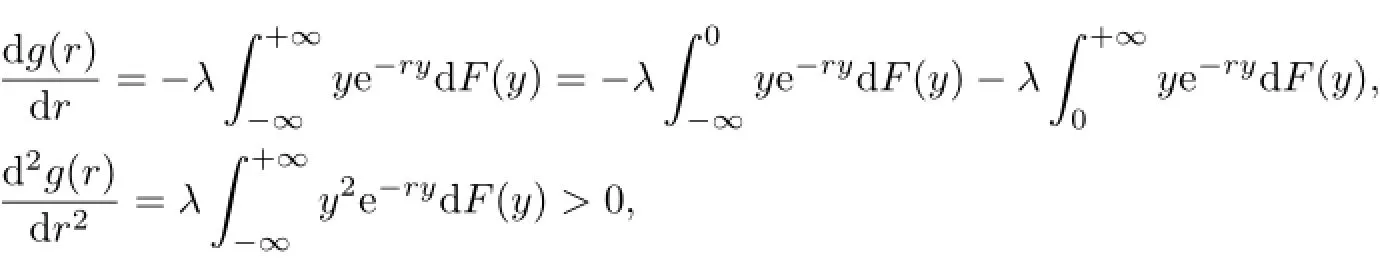
g(r)is a convex function.As a result，the equation g(r)=0 has at most two solutions. Also，r=0 is its trivial solution.Moreover，we have

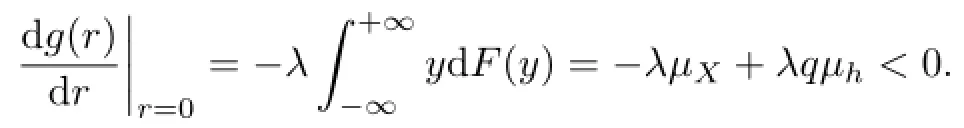
As r→+∞，

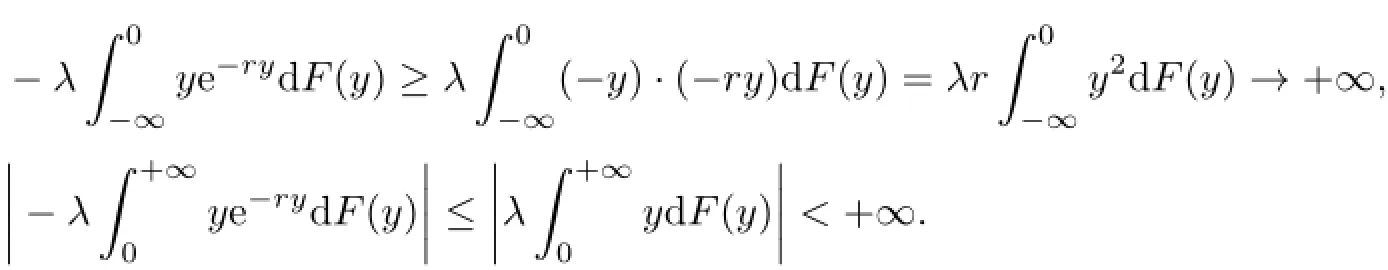
Proof.First，Muis measurable with respect to Fs.Then，we claim that E[Mu(t)]＜∞. In fact，we have

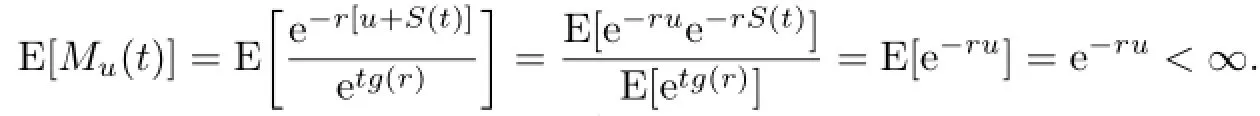
Finally，for every 0≤v＜t，we can attain from Lemma 4.1 that

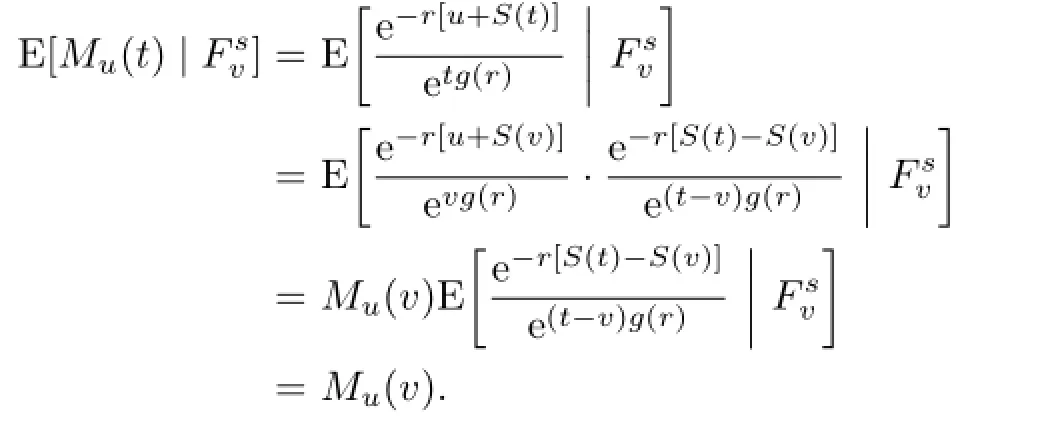
Hence，{Mu(t)，Fst，t≥0}is martingale by the definition of martingale.

Lemma 4.3T is the stopping time of Fs.

Proof.For

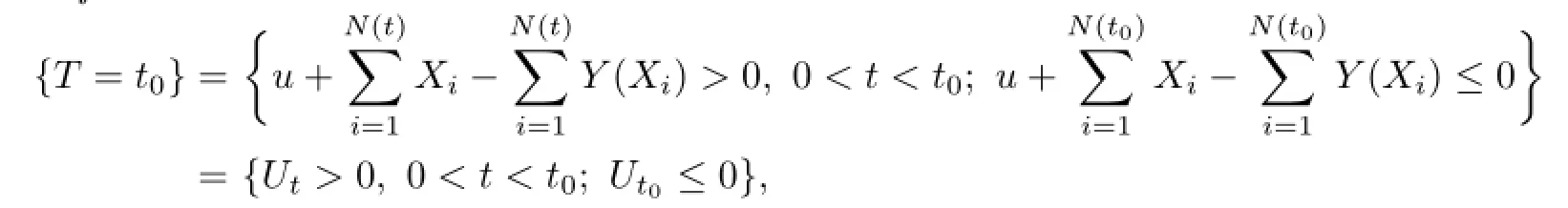
whether the event{T=t0}occurs or not depends fully on the state of the time t0and before t0.Therefore，T is the stopping time of Fs.

Theorem 4.1For the Poisson model{U(t)，t≥0}，where premium and claim income are dependent，its probability of ultimate ruin meets the inequality Ψ(u)≤e−Ru，where R is the adjustment coefficient.

Proof.For T is the stopping time of Fs，we choose t0＜∞.In this case，t0∧T is also the stopping time of Fs.According to Lemma 4.2 and the stopping time theorem，we have

Under the condition{T＜∞}，we have u+S(T)＜0.Thus

We let t0→∞in both sides of the above equation(4.4)，and there is Ψ(u)≤e−Ru，where R is the adjustment coefficient.

Theorem 4.2For the Poisson model{U(t)，t≥0}，where premium and claim income are dependent，its probability of ultimate ruin is

Proof.Let r=R in equation(4.3)，and we can attain

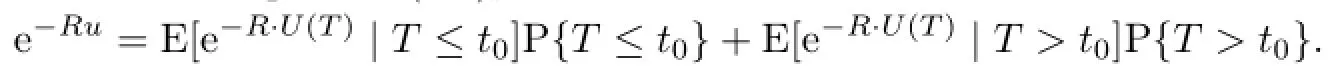
Denote characteristic function of a set A by I{A}，and there is the conclusion

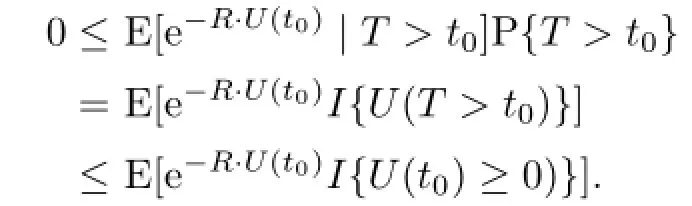
For 0≤e−R·U(t0)I{U(t0)≥0)}≤1，using the law of large numbers，we can prove that U(t0)→∞when t0→∞.Therefore，using Dominated Convergence Theorem，we have

Letting t0→∞in both sides of the above equation，we can achieve the conclusion.

References

[1]Lundberg F.I.Approximerad Framst¨allning af Sannolikhetsfunktionen；II.˚Aterf¨ors¨akring af Kollektivrisker.Uppsala:Almqvist&Wiksells，1903.

[2]Cram´er H.On the Mathematical Theory of Risk.Stockholm:Skandia Jubilee Volume，1930.

[3]Zhang S.The problem of ruin probability in risk theory(in Chinese).Master Degree Thesis，Jilin University，Changchun，2008.

[4]Mao Z C.A risk model and its ruin probability with compound poisson-geometric counting process(in Chinese).Acta Math.Appl.Sin.，2005，28(3):419–428.

[5]Gerber H U.An extension of the renewal equation and its application in the collective theory of risk.Scand.Actuar.J.，1970，1970(3-4):205–210.

[6]Shiu E S W.The probability of eventual ruin in the compound binomial model.Astin Bull.，1989，19(2):179–190.

[7]Grandell J.Aspects of Risk Theory.New York:Springer Verlag，1991.

[8]Kluppelberg C，Mikosch T.Large deviations of heavy-tailed random sums with applications to insurance and finance.J.Appl.Probab.，1997，34(2):293–308.

[9]Asmussen S，Albrecher H.Ruin Probabilities.Singapore:World Scientific，2010:424–427.

[10]Wang K Y，Wang Y B，Gao Q W.Uniform asymptotics for the finite-time ruin probability of a dependent risk model with a constant interest rate.Methodol.Comput.Appl.Probab.，2013，15(1):109–124.

[11]Ambagaspitiya R S.Ultimate ruin probability in the sparre andersen model with dependent claim sizes and claim occurrence times.Insurance Math.Econom.，2009，44(3):464–472.

[12]Albrecher H，Boxma O J.A ruin model with dependence between claim sizes and claim intervals.Insurance Math.Econom.，2004，35(2):245–254.

[13]Zhang X M.The research of bankruptcy model in insurance company(in Chinese).Master Degree Thesis，Southwest Jiaotong University，Chengdu，2011.

[14]Zhang Z J.Research on ruin theory and its applications in financial mathematics(in Chinese). Master Degree Thesis，Jilin university，Changchun，2006.

[15]Cizek P，H¨ardle W K，Weron R.Statistical Tools for Finance and Insurance.Berlin Heidelberg: Springer Science&Business Media，2005.

10.13447/j.1674-5647.2016.03.06

date:May 11，2015.

The NSF(11271155，J1310022)of China.

*Corresponding author.

E-mail address:wangdh@jlu.edu.cn(Wang D H)，zhangxl@jlu.edu.cn(Zhang X L).