Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality

Piao Yong-jie

(Department of Mathematics，College of Science，Yanbian University，Yanji，Jilin，133002)

Communicated by Ji You-qing



Common Fixed Point Theorems and Q-property for Quasi-contractive Mappings under c-distance on TVS-valued Cone Metric Spaces without the Normality

Piao Yong-jie

(Department of Mathematics，College of Science，Yanbian University，Yanji，Jilin，133002)

Communicated by Ji You-qing

Fixed point and common fixed point results for mappings satisfying quasicontractive conditions expressed in the terms of c-distance on TVS-valued cone metric spaces(without the underlying cone which is not normal)are obtained，and P-property and Q-property for mappings in the terms of c-distance are discussed.Our results generalize and improve many known results.

TVS-valued cone metric space，quasi-contractive condition，common fixed point，P-property，Q-property

2010 MR subject classification:47H05，47H10，54E40，54H25

Document code:A

Article ID:1674-5647(2016)03-0229-12

1　Introduction and Preliminaries

Huang and Zhang[1]have introduced the concepts of cone metric spaces，where the set of real numbers is replaced by an order Banach space.Du et al.[2]–[10]discussed the existence problems of fixed points and common fixed points for mappings defined on TVS-valued cone metric spaces，where the order Banach space is replaced by a topological vector space.

Fixed point results in metric spaces with the so-called w-distance were obtained for the first by Kada et al.[11]，where non-convex minimization problems were treated.Further results were given in[12]–[14].The cone metric version of this notion(usually called a c-distance)was used in[15]–[16].

Wang and Guo[17]obtained a fixed point theorem for a mapping in normal cone metricspace under some contractive condition expressed in the terms of c-distance，and Djordjevi´c et al.[18]also obtained fixed point and common fixed point results for mappings in TVS-valued non-normal cone metric spaces under contractive condition expressed in the terms of c-distance.Those results generalize the corresponding results in[11]–[16]and the related results.

Here，we discuss the existence problems of fixed points and common fixed points for mappings on TVS-valued non-normal cone metric spaces under quasi-contractive condition expressed in the terms of c-distance and P-property and Q-property.The obtained results generalize the conclusions in[17]–[18]and other corresponding fixed point and common fixed point theorems.

Let(E，τ)be a topological vector space(TVS)，P0a nonempty subset of E.P0is said to be a cone whenever

(i)P0is closed，nonempty and

(ii)ax+by∈P0for all x，y∈P0and real numbers a，b≥0；

(iii)P0∩(-P0)={0}.

In this paper，we always assume that the cone P0has a nonempty interior，i.e.，int(such cones are called solid).

For a given cone P0⊂E，we define a partial ordering≤with respect to P0by x≤y if and only if y-x∈P0.x＜y stands for x≤y andx≪y stands for y-x∈intP0.

A cone P0is called normal if there exists a real number K＞0 such that for all x，y∈E，

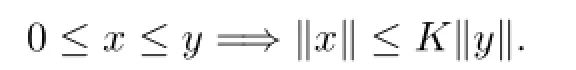
The least positive number K satisfying the above condition is called the normal constant of P0.

It is known that a metric space is a normal cone metric space with normal constant K=1.

Definition 1.1Let X be a nonempty set and E a TVS with solid cone P0.Suppose that the mapping d:X×X→E satisfies

(1)0≤d(x，y)for all x，y∈X，and d(x，y)=0 if and only if x=y；

(2)d(x，y)=d(y，x)for all x，y∈X；

(3)d(x，y)≤d(x，z)+d(z，y)for all x，z，y∈X.

Then d is called a TVS-valued cone metric on X，(X，d)is called a TVS-valued cone metric space.

Definition 1.2Let(X，d)be a TVS-valued cone metric space，x∈X and{xn}n∈N+a sequence in X.Then

(1){xn}is a Cauchy sequence whenever for every c∈E with 0≪c there exists an N∈N+such that d(xm，xn)≪c for all n，m＞N；

(2){xn}converges to x whenever for every c∈E with 0≪c，there exists an N∈N+such that d(xn，x)≪c for all n＞N.We denote this by

(3)(X，d)is called complete if every Cauchy sequence in X is convergent.

We shall make use of the following properties:

(P1)If u，v，w∈E，u≤v and v≤w，then u≤w.

(P2)If u≤λu，where u∈P0and 0≤λ＜1，then u=θ.

Definition 1.3Let(X，d)be a TVS-valued cone metric space.A function q:X×X→E is called a c-distance on X，if

(1)θ≤q(x，y)for all x，y∈X；

(2)q(x，z)≤q(x，y)+q(y，z)for all x，y，z∈X；

(3)a sequence{yn}in X converges to a point y∈X，and for some x∈X and u=ux∈P0，q(x，yn)≤u holds for each n∈N+，then q(x，y)≤u；

(4)for each c∈E with θ≪c，there exists an e∈E with θ≪e such that q(z，x)≪e and q(z，y)≪e implies d(x，y)≪c.

The following facts can be found in[17]–[18].

1.Every w-distance must be a c-distance on TVS-valued cone metric spaces.

2.There are many examples of c-distances on TVS-valued cone metric spaces but not c-distance on cone metric spaces，see[11].

3.For c-distance q，

1)q(x，y)=q(y，x)does not necessarily hold for all x，y∈X；

2)q(x，y)=0 is not necessarily equivalent to x=y.

Definition 1.4A sequence{un}in P0is said to be a c-sequence if for each c≫0 there exists an n0∈N+such that un≪c for all n≥n0.

Obviously，if{un}and{vn}are c-sequences in E and α，β＞0，then{αun+βvn}is a c-sequence.

Definition 1.5Let(X，d)is a TVS-valued cone metric space，f:X→X a mapping and x0∈X.If for each c∈E with c≫0，there exists a b∈E with b≫0 such that x∈X，d(x，x0)≪b implies d(fx，fx0)≪c，then we say that f is continuous at x0.f is said to be continuous on X if f is continuous at every x∈X.

Lemma 1.1[18]Let(X，d)be a TVS-valued cone metric space，q a c-distance on X. Suppose that{xn}and{yn}are two sequences in X and x，y，z∈X.If{un}and{vn}are two c-sequences in P0，then the following properties hold:

(1)If q(xn，y)≤unand q(xn，z)≤vnfor any n∈N+，then y=z.In particular，if q(x，y)=0 and q(x，z)=0，then y=z.

(2)If q(xn，xm)≤unfor all m＞n＞n0，then{xn}is a Cauchy sequence in X.

Adopting the proof process of Lemma 2 in[19]，we can obtain the following result:

Lemma 1.2Let(X，d)be a TVS-valued cone metric space，f:X→X a mapping and x0∈X.Then f is continuous at x0if and only if xn→x0as n→∞implies fxn→fx0as n→∞.

2　Fixed Points and Common Fixed Points under c-distance

Theorem 2.1Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance，m and n be two positive integers.Suppose that two mappings f，g:X→X are commutable，fmand gnare both onto and continuous.If for every x，y∈X，

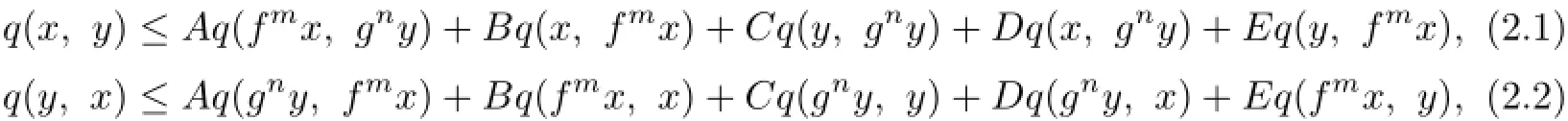
where A，B，C，D，E≥0 and A+B+C+2D+2E＜1，then f and g have a unique common fixed point u∈X with q(u，u)=0.

Proof.By the subjectivity of fmand gn，we take x0∈X and constructsatisfying

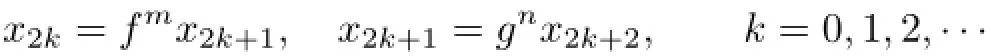
For any k=0，1，2，···，by(2.1)and(2.2)respectively，one has

Let

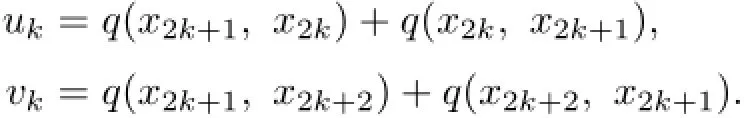
Adding up(2.3)and(2.4)，we obtain

Similarly，by(2.2)and(2.1)respectively，we obtain

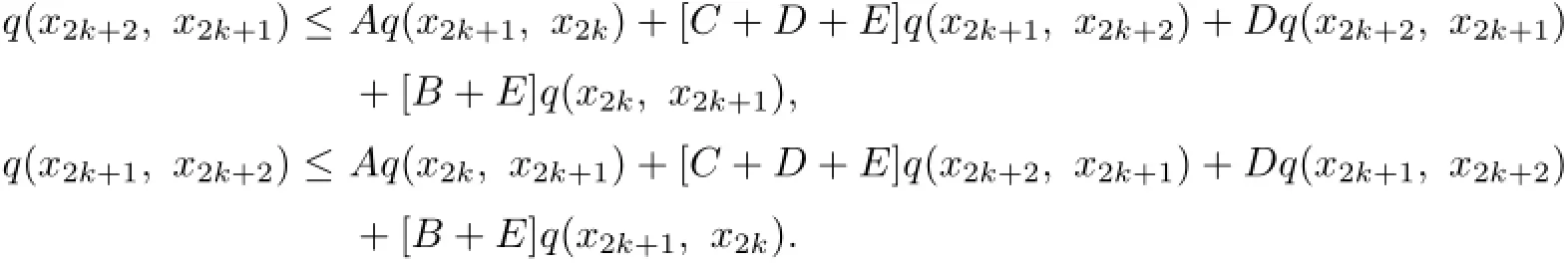
Adding up the above two formulas，we obtain

Let h=h1h2.Then 0＜h＜1.And from(2.5)and(2.6)，we obtain

Hence，by using the mathematical induction，we obtain

Since q(x2k，x2k+1)≤ukand q(x2k+1，x2k+2)≤vk，so

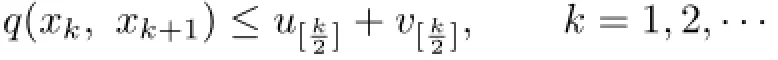
Hence，for any α，β∈N+with β＞α≥1，

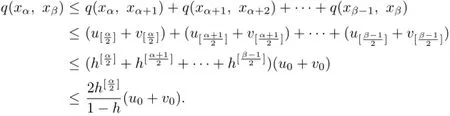
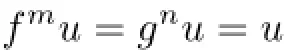
by the continuity of fmand gn.

In view of(2.1)，

q(u，u)≤Aq(fmu，gnu)+Bq(u，fmu)+Cq(u，gnu)+Dq(u，gmu)+Eq(u，fmu) =[A+B+C+D+E]q(u，u)，

hence

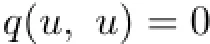
by(P2)(since 0＜A+B+C+D+E＜A+B+C+2D+2E＜1).

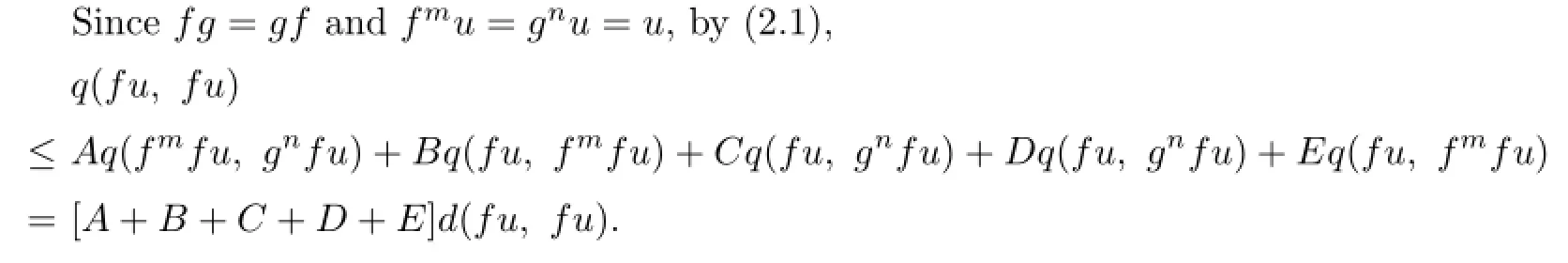
Hence，by(P2)，

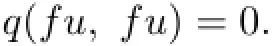
Similarly，we have

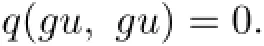
By using(2.1)and(2.2)respectively，we obtain the following two conclusions:

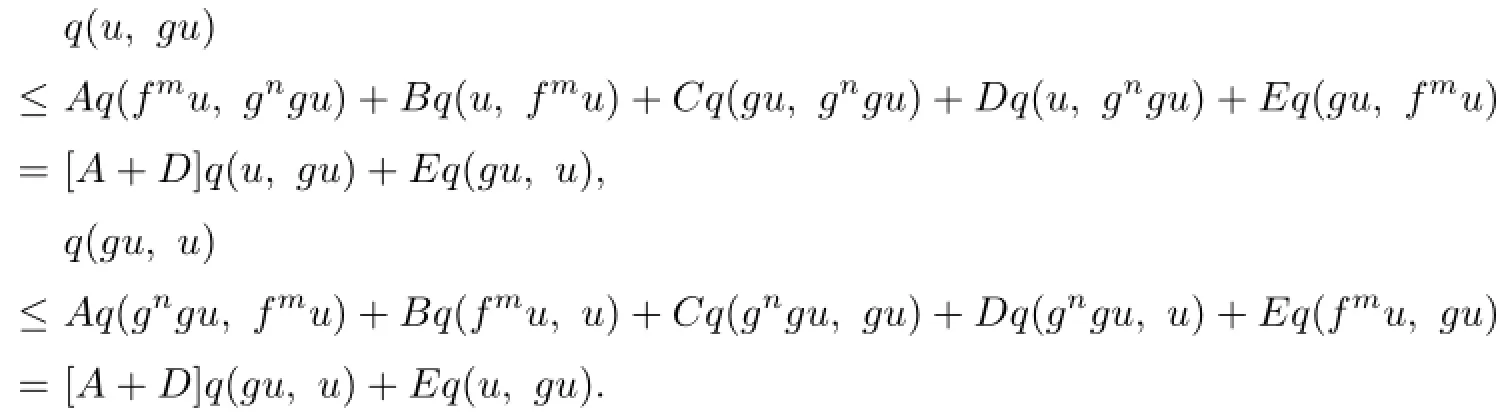
Adding up the above two formulas，we obtain

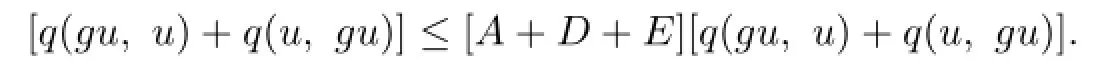
Hence

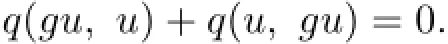
So

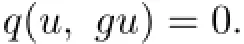
But q(u，u)=0，hence，by Lemma 1.1(1)，

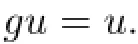
Similarly，by using(2.1)and(2.2)respectively，we obtain

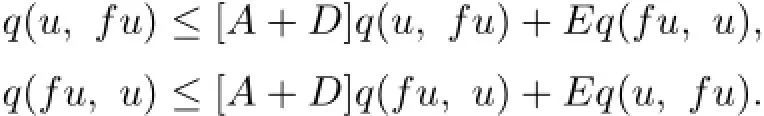
Adding up the two formulas，we obtain

Hence

and therefore

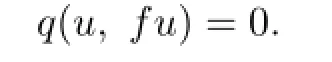
So

Thereby u is a common fixed point of f and g.

If v is a common fixed point of f and g，then by(2.1)and(2.2)respectively，

Adding up the two above，we obtain

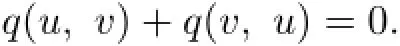
Hence

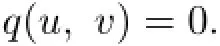
Therefore，by Lemma 1.1(1)，u=v.The proof is completed.

The following results is a particular form of Theorem 2.1.

Theorem 2.2Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance，m and n be two positive integers and α，β，γ≥0.Suppose that two mappings f，g:X→X are commutable，fmand gnare both onto and continuous.If for every x，y∈X，

Proof.Let A=α，B=C=β，D=E=γ.Then the conclusion follows from Theorem 2.1.

Next，we give the non-commutable version of Theorem 2.1.

Theorem 2.3Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance，m and n be two positive integers.Suppose that two mappings f，g:X→X satisfy that fmand gnare both onto and continuous.If(2.1)and(2.2)hold for every x，y∈X，where A，B，C，D，E≥0 with A+2B+2C+2D+2E＜1，then f and g have a unique common fixed point u∈X with q(u，u)=0.

Proof.Just as the proof of Theorem 2.1，there exist a Cauchy sequence{xn}and an element u∈X satisfying xn→u as n→∞and fmu=gnu=u with q(u，u)=0.

By(2.1)and(2.2)respectively，we have

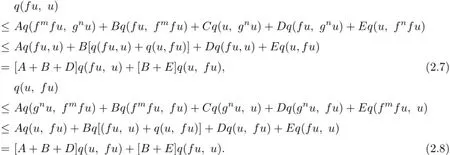
Adding up(2.7)and(2.8)，we obtain

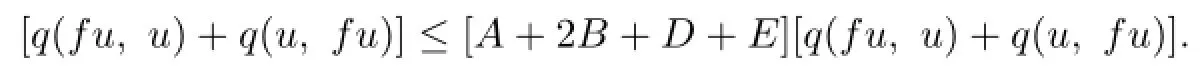
Hence

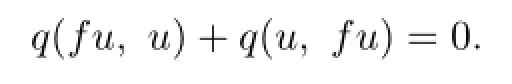
So

Therefore，

Similarly，by(2.1)and(2.2)respectively，we have

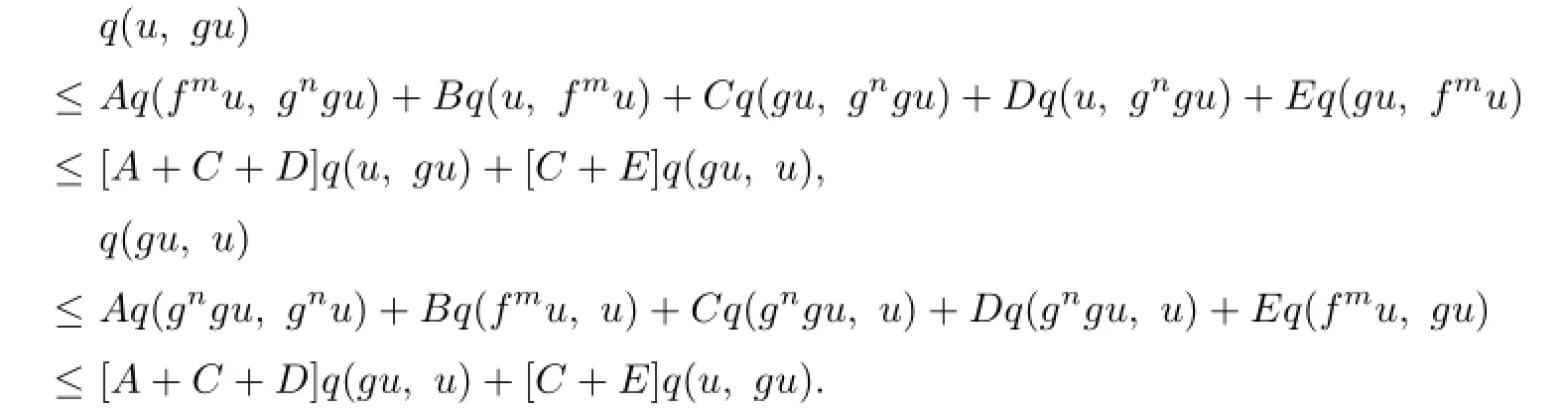
Adding up the above two formulas，we have

Hence

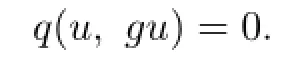
Therefore，

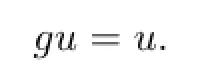
So u is a common fixed point of f and g.

The rest is similar to the proof of Theorem 2.1.The proof is completed.

The following result is a particular case of Theorem 2.3 and also a non-commutable version of Theorem 2.2.

Theorem 2.4Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance，m and n be two positive integers and α，β，γ≥0.Suppose that two mappings f，g:X→X satisfy that fmand gnare both onto and continuous.If for every x，y∈X，

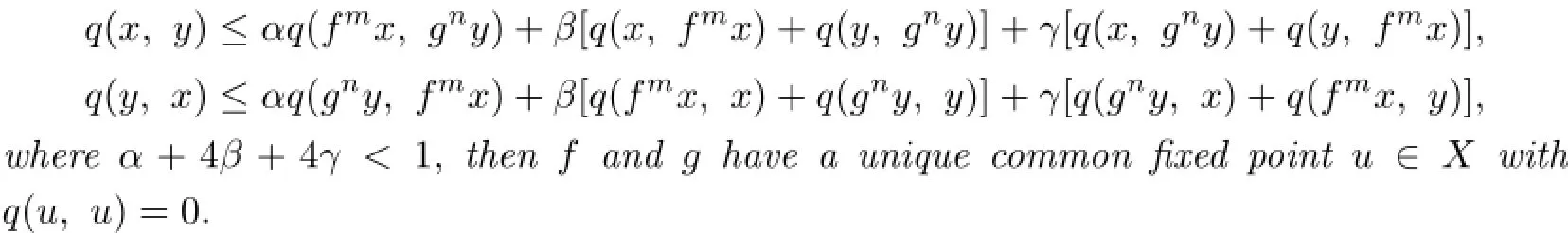
3　Another Class of Common Fixed Point and P(Q)-property

A mapping f:X→X is said to have P-property if f satisfies

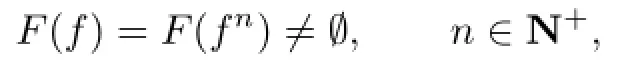
where F(f)denotes the set of fixed points of f.Two mappings f，g:X→X are said to have Q-property if f，g satisfy

Theorem 3.1Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance. Suppose that two onto and commutable and continuous mappings f，g:X→X satisfy

where λ∈(0，1).Then f and g have a common fixed point u∈X with q(u，u)=0 and Q-property.

Proof.Take x0∈X and construct a sequencesatisfying

For any n=1，2，···，by using(3.1)and(3.2)respectively，we obtain

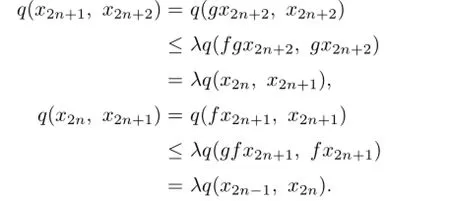
Hence，by the mathematical induction，

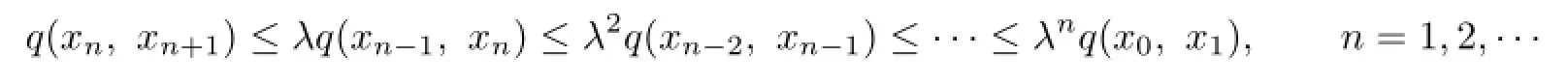
Therefore，for any m＞n≥1，

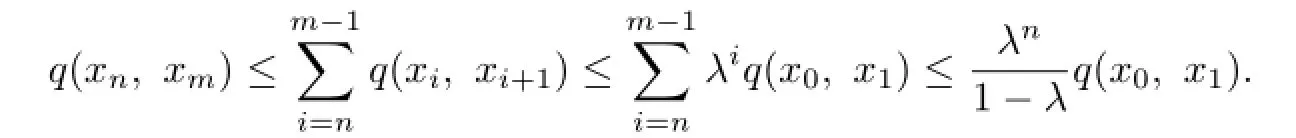
So{xn}is Cauchy by Lemma 1.1(2).Hence，there is a u∈X such that xn→u as n→∞by the completeness of X.Therefore

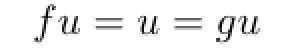
by the continuity of f and g，i.e.，F(f)∩F(g)̸=∅.

Since

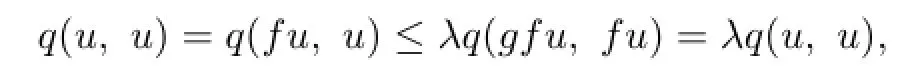
we know q(u，u)=0 by(P2).

Obviously，

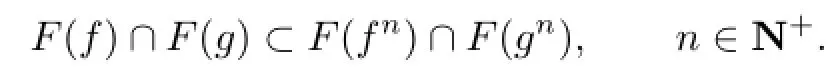
Fix any n∈N+and take u∈F(fn)∩F(gn).For any k=1，2，···，n，by(3.1)and(3.2)，we have

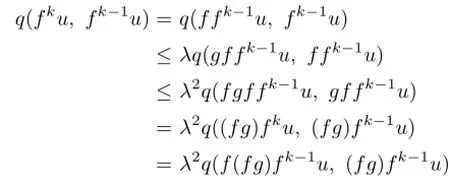
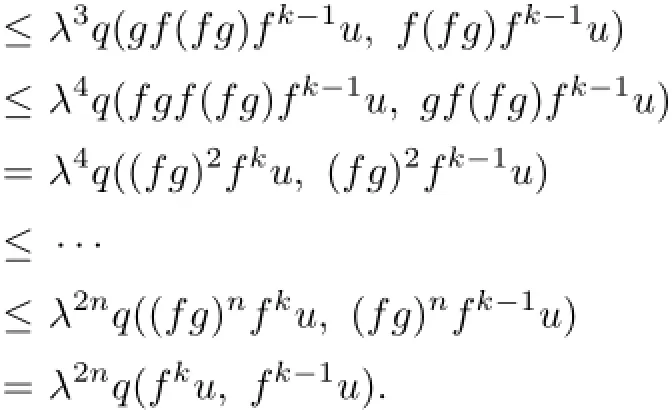
Hence，by(P2)，

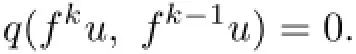
Therefore，

Similarly，we have

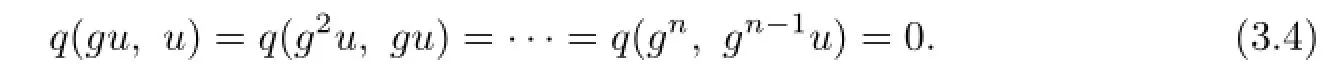
By(3.3)，for any k=1，2，···，n，we have

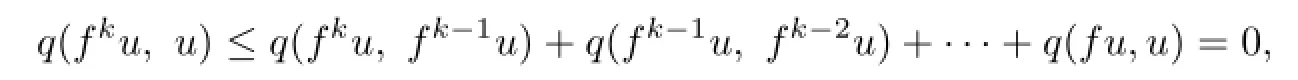
hence

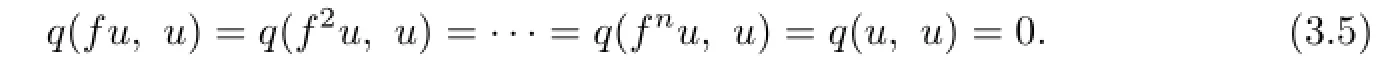
Similarly，by(3.4)，we have

By using(3.1)and(3.6)，we obtain

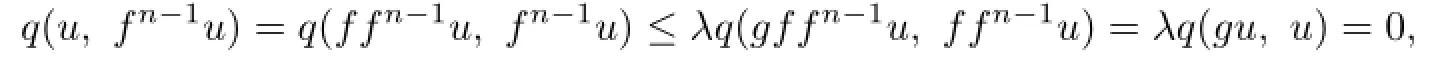
i.e.，

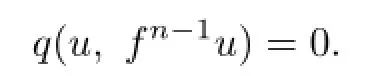
Hence

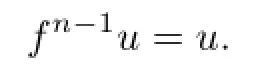
Similarly，

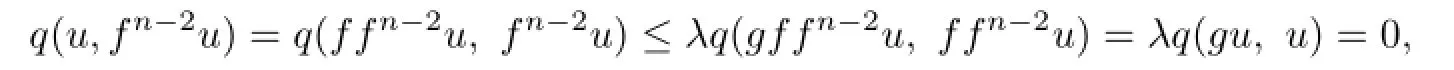
i.e.，

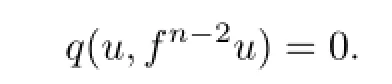
Hence fn−2u=u.

Repeating this process，we obtain

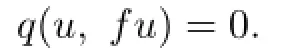
Hence fu=u.

Similarly，by(3.2)and(3.5)，gu=u.Hence u∈F(f)∩F(g).Thereby

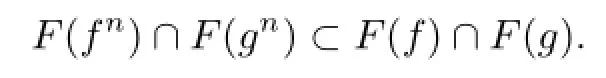
So

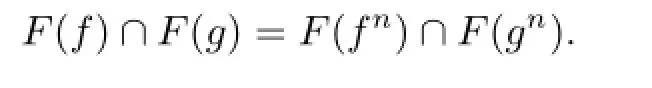
Theorem 3.2Let(X，d)be a complete TVS-valued cone metric space，q be a c-distance. Suppose that a onto and continuous mapping f:X→X satisfies

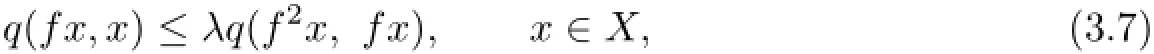
where λ∈(0，1).Then f has a fixed point u∈X with q(u，u)=0 and P-property.

Proof.Let f=g in Theorem 3.1.Then(3.1)and(3.2)deduce to(3.7).

Example 3.1Let E=C1R[0，1]and define a norm on E as

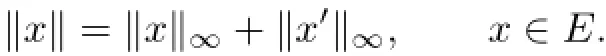
Let P0={x∈E:x≥0}.Then E is a Banach space with a non-normal cone P(see[20] and[21]).

Let X=[0，∞)and define d:X×X→E as

Then(X，d)is a TVS-valued cone metric space with a non-normal cone P0.

Define q:X×X→E as

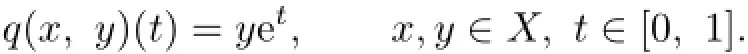
Then it is easy to know that q is a c-distance on X by Example 2.14 in[22].

Let f:X→X，fx=2x for all x∈X and take.Then，for any x∈X，

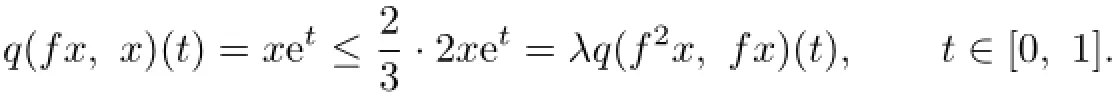
Hence

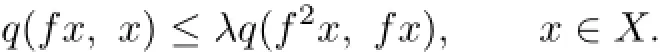
So f and λ satisfy all conditions of Theorem 3.2，therefore f has a fixed point 0.Obviously，q(0，0)=0 and f has P-property.

Remark 3.1The condition(3.7)in Theorem 3.2 is equivalent to the following condition

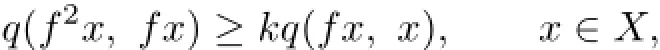
where k＞1.Hence Theorem 3.2 is a new fixed point theorem for a generalized I-expansive mapping(see[23])under c-distance on TVS-valued metric spaces.

References

[1]Huang L G，Zhang X.Cone metric spaces and fixed point theorems of contractive mappings. J.Math.Anal.Appl.，2007，332(2):1468–1476.

[2]Du W S.A note on cone metric fixed point theory and its equivalence.Nonlinear Anal.，2010，72:2259–2261.

[3]Kadelburg Z，Radenovi´c S，Rako˘cevi´c V.Topological vector space valued cone metric spaces and fixed point theorems.Fixed Point Theory Appl.，2010，2010(1):1–17.

[4]Abdeljawad Th，Karapinar E.A gap in the paper“A note on cone metric fixed point theory and its equivalence，Nonlinear Anal.2010，72:2259–2261”.Gazi Univ.J.Sci.2011，24(2): 233–234.

[5]Abdeljawad Th，Karapinar E.A common fixed point theorem of Gregus type on convex cone metric spaces.J.Comput.Anal.Appl.，2011，13(4):609–621.

[6]Arandjelovi´c I D，Ke˘cki´c D J.On nonlinear quasi-contractions on TVS-valued cone metric spaces.Appl.Math.Lett.，2011，24:1209–1213.

[7]Karapinar E，Yuksel U.On common fixed theorem without commuting conditions in TVS-cone metric spaces.J.Comput.Anal.Appl.，2011，13:1123–1131.

[8]Simi´c S S.A note on Stone’s，Baire’s，Ky Fan’s and Dugundji’s theorems in TVS-cone metric spaces.Appl.Math.Lett.2011，24:999–1002.

[9]Jankovi´c S，Kadelburg Z，Radenovi´c S.On cone metric spaces，a survey.Nonlinear Asnal.，2011，74:2591–2601.

[10]Piao Y J，Jin H L，Jin Y F.Unique common fixed points for mappings on TVS-valued cone metric spaces.Acta Math.Sci.，2015，35A(1):172–181.

[11]Kada O，Suzuki T，Takahashi W.Nonconvex minimization theorems and fixed point theorems in complete metric spaces.Math.Japonica.，1996，44:381–391.

[12]Abbas M，Ili´c D，Ali Khan M.Coupled coincidence point and coupled common fixed point theorems in partially ordered metric spaces with w-distance.Fixed Point Theory Appl.，2010，2010(1):395–400.

[13]Ili´c D，Rako˘cevi´c V.Common fixed point for maps with w-distance.Appl.Math.Comput.，2008，199:599–610.

[14]Razani A，Nezhad Z M，Boujary M.A fixed point theorem for w-distance.Appl.Sci.，2009，11:114–117.

[15]Chp Y J，Saadati R，Wang S H.Common fixed point theorems on generalized distance in ordered cone metric spaces.Comput.Math.Appl.，2011，61:1254–1260.

[16]Lakzian H，Arabyani F.Some fixed point theorems in cone metric spaces with w-distance. Inter.J.Math.Anal.，2009，22(3):1081–1086.

[17]Wang S H，Guo B H.Distance in cone metric spaces and common fixed point theorems.Appl. Math.Lett.，2011，24:1735–1739.

[18]Djordjevi´c M，Dori´c D，Kadelburg Z，et al.Fixed point results under c-distance in TVS-cone metric spaces.Fixed Point Theory Appl.，2011，2011(1):1–9.

[19]Piao Y J.Fixed point theorems for III，s-III type expansive mappings on CMTS.J.Systems Sci.Math.Sci.，2013，33(8):976–984.

[20]Xu S Y，Radenovi´c S.Fixed point theorems of generalized Lipschitz mappings on cone metric spaces over Banach algebras without assumption of normality.Fixed Point Theory Appl..2014，2014(1):1–12.

[21]Rezapour S，Hamlbarani R.Some note on the paper“Cone metric spaces and fixed point theorems of contractive mappings”.J.Math.Anal.Appl.，2008，345:719–724.

[22]Cho Y J，Saadati R，Wang S.Common fixed point theorems on generalized distance in ordered cone metric spaces.Comput.Math.Appl.，2011，61:1254–1260.

[23]Wang S Z，Li B Y，Gao Z M.Expansive mappings and fixed point theorems.Adv.Math. (China).1982，11(2):149–153.

10.13447/j.1674-5647.2016.03.05

date:July 2，2015.

The NSF(11361064)of China.

E-mail address:sxpyj@ybu.edu.cn(Piao Y J).