Measures of Asymmetry Dual to Mean Minkowski Measures of Asymmetry for Convex Bodies

Yao Dan and Guo Qi

(Department of Mathematics，Suzhou University of Science and Technology，Suzhou，Jiangsu，215009)

Communicated by Ji You-qing



Measures of Asymmetry Dual to Mean Minkowski Measures of Asymmetry for Convex Bodies

Yao Dan and Guo Qi*

(Department of Mathematics，Suzhou University of Science and Technology，Suzhou，Jiangsu，215009)

Communicated by Ji You-qing

We introduce a family of measures(functions)of asymmetry for convex bodies and discuss their properties.It turns out that this family of measures shares many nice properties with the mean Minkowski measures.As the mean Minkowski measures describe the symmetry of lower dimensional sections of a convex body，these new measures describe the symmetry of lower dimensional orthogonal projections. Key words:mean Minkowski measure，asymmetry，symmetry，simplex

2010 MR subject classification:52A20，52A38，52A39，52A40

Document code:A

Article ID:1674-5647(2016)03-0207-10

1　Introduction

In the recent years，the measures of asymmetry(or symmetry)，formulated by Gr¨unbaum[1]for convex bodies(i.e.，compact convex sets with nonempty interior in the standard Euclidean spaces)have drawn renewed attentions in convex geometry(see[2]–[10]and the references therein).

Among known measures of asymmetry(or symmetry)，the Minkowski measure is probably the most important one，which has various generalizations and extensions(see，e.g.，[5]–[7]and[9]).Among these generalizations，Toth[6]introduced a family of measures(functions)of symmetry σm，m≥1，called the mean Minkowski measures of symmetry(see below for definition)，and did a systematic study on them in a series of papers(see[6]–[10]). Roughly speaking，for a convex body K，its(mth)mean Minkowski measure of symmetryσmis a function defined on intK，the interior of K，which，when 1≤m≤n，provides information of the shapes of m-dimensional sections of K.

As a main result of this paper，we introduce another family of measures(functions)of symmetry，m≥1，defined on intK as well，called the dual mean Minkowski measures of symmetry，which in a sense are the dual concept of the mean Minkowski measures.It turns out，for 2 or 3 dimensional convex bodies，that the dual mean Minkowski measures share almost all nice properties with the mean Minkowski measures and，to some extent，describe the shapes of projections of a convex body to lower dimensions.

2　Preliminaries

Denote by Rnthe n-dimensional standard Euclidean space，and by Knthe family of all convex bodies in Rn.denotes the canonical inner product on Rnand d(·，·)denotes the metric induced by this inner product.For a subset S⊂Rn，convS，coneS denote the convex hull，the convex conical hull of S respectively，and linS denotes the linear subspace generated by S.Sn−1denotes the(n-1)-dimensional unit sphere and∆n(or∆simply) denotes an n-dimensional simplex(or n-simplex simply)，i.e.，∆n=conv{v0，v1，···，vn}∈Rn，where v0，v1，···，vn，called the vertices of∆n，are affinely independent.For other standard notations we refer to[11].

A function f:Rn→R is called affine if f(αx+βy)=αf(x)+βf(y)for any x，y∈Rnand α，β∈R.It is known that for any affine function f，there are unique u∈Rnand b∈R such that f(·)=

Denote by Aff(Rn)the family of all affine functions，called the affine dual space of Rn，which is a linear space under the ordinary addition and scalar multiplication of functions and can be identified with Rn+1in a natural way(see[4]and[11]).

We recall the mean Minkowski measures defined by Toth[6]–[7].

Let K∈Kn.The distortion function Λ:∂K×intK→R is defined by

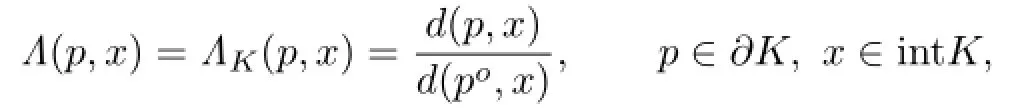
where podenotes the opposite boundary point of p against x.

Let m≥1 and x∈intK.A multi-set{p0，p1，···，pn}，where pi∈∂K and repetition is allowed，is called an m-configuration with respect to(w.r.t.for brevity)x if x∈conv{p0，p1，···，pn}.The set of m-configurations w.r.t.x is denoted by Cm(x)=CK，m(x).

Definition 2.1[8]Let K∈Knand m≥1.We define its(mth)mean Minkowski measure (function)σm=σK，m:intK→R by

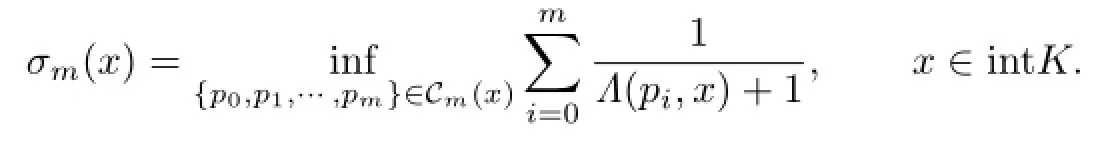
The sequence{σm}m≥1has many nice properties，e.g.，Toth[7]proved that{σm}m≥1is sub-arithmetic(which is a crucial tool in Toth’s work)，i.e.，for any m，k≥1，x∈intK，

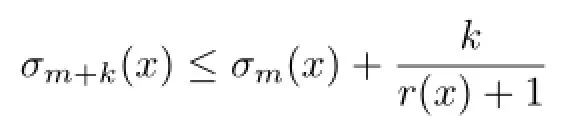
with equalities hold when m=n，wherethe Minkowski measure，and that

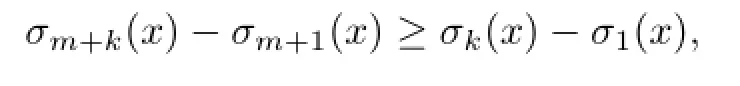
and，as a consequence，{σm}m≥1is monotone(writing m=(m-1)+1 and then applying the inequality above and the fact σm≥1).

The following is one of the main results of Toth’s.

Theorem 2.1[6]For any K∈KnandMoreover，σm(x)=1 for some x∈intK if and only if m≤n and K has an m-simplex section through x，i.e.，there is an m-dimensional affine subspace H containing x such that K∩H is an m-simplex； forfor some x∈intK if and only if K is centrally symmetric w.r.t. x.

From the above theorem，we see that{σm}m≥1indeed provides the information of lowdimensional sections of a convex body.

In this paper，we introduce another family of measures，which provides the information of low-dimensional projections of a convex body.

3　m-supporting Configurations

In order to define our measures of asymmetry，in this section we introduce first the concept of m-supporting configurations and then study their properties.

Given K∈Kn，we denote(see[4]–[5])

Definition 3.1Let K∈Knand m≥1.A multi-set(repetition allowed)is called an m-support configuration of K if

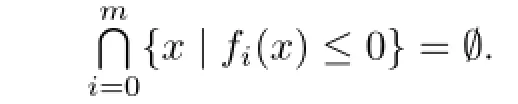
The family of m-support configurations of K is denoted by

Remark 3.1Unlike the m-configurations，m-support configurations are independent of the points in intK.

The following are some properties of m-support configurations.

Proposition 3.1Let f0，f1，···，fm

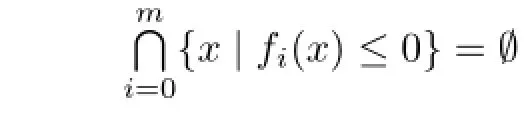
if and only if

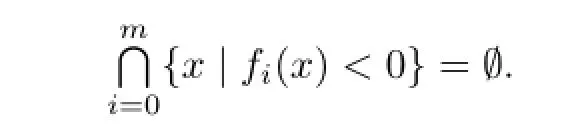
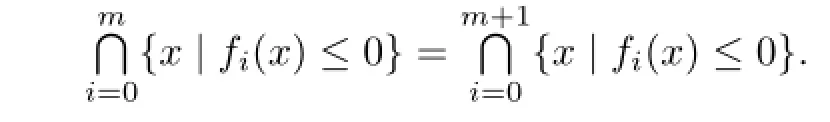
Theorem 3.1Let K∈Knand f0，f1，···whereThen the following statements are equivalent:

(1){f0，f1，···，fm}∈；

(2)for any u∈Rn，for some i；

(3)cone{ui0，···，uit}=lin{ui0，···，uit}for some t≥1 and i0，···，it.

Proof.(1)⇒(2).Assume that there exists a non-zero u∈Rnsuch thatfor all i，i.e.，⟨ui，-u⟩＜0 for all i.Thus，since， we have-for sufficiently large λ，a contradiction.

(3)⇒(1).Suppose，say，cone{u0，···，ut}=lin{u0，···，ut}for some t≥1.Then we havewith at least one αiis positive.Thus，setting

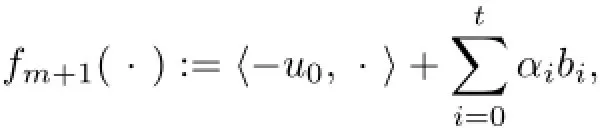
we have，by Proposition 3.2，

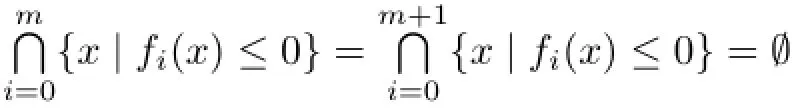
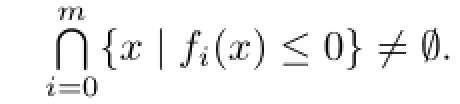
Then，by Proposition 3.1，

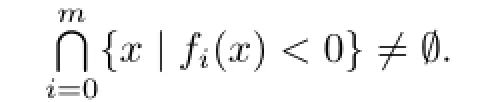
4　Dual Mean Minkowski Measure

In this section，we define a family of measures of asymmetry in terms of the support configurations and study their properties.First，we have the following definition.

Definition 4.1Let K∈Knand m≥1.Then its(mth)dual mean Minkowski measure (function):intK→R is defined by

(3)By Proposition 3.4 and the fact thatis continuous w.r.t.{f0，···，fm}∈，we see that the infimum in the definition ofis attainable.

An m-support configuration{f0，···，fm}is called a(m-)minimizer w.r.t.x if

Now，we discuss the properties of the dual mean Minkowski measures，which are similar to those of the mean Minkowski measures.The following theorem，which states that the sequenceis sub-arithmetic，is crucial in the study of the dual mean Minkowski measures.

Theorem 4.1Let K∈Knand m，k≥1.Then for any x∈intK，

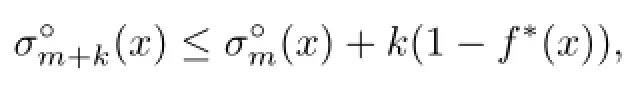
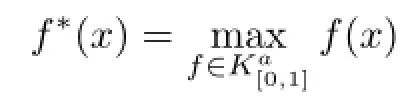
or equivalently

the Minkowski measure.Moreover，when m=n the equality holds，i.e.，the sequenceis arithmetic.

Proof.By adding k copies of f∗to an m-support configuration{f0，···，fm}，we have clearly an(m+k)-support configuration{f0，···，fm，f∗，···，f∗}.Thus

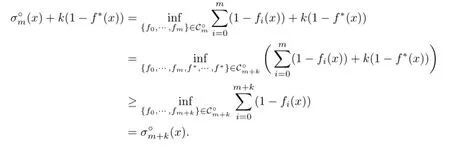
which clearly leads to

and further，together with the above general inequality，leads to

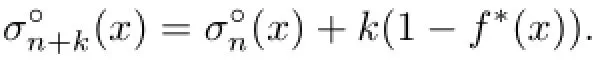
This completes the proof.

As an application of Theorem 4.1，we show the following theorem.

Theorem 4.2Let K∈Knand m，k≥1.Then

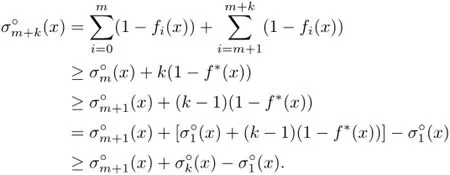
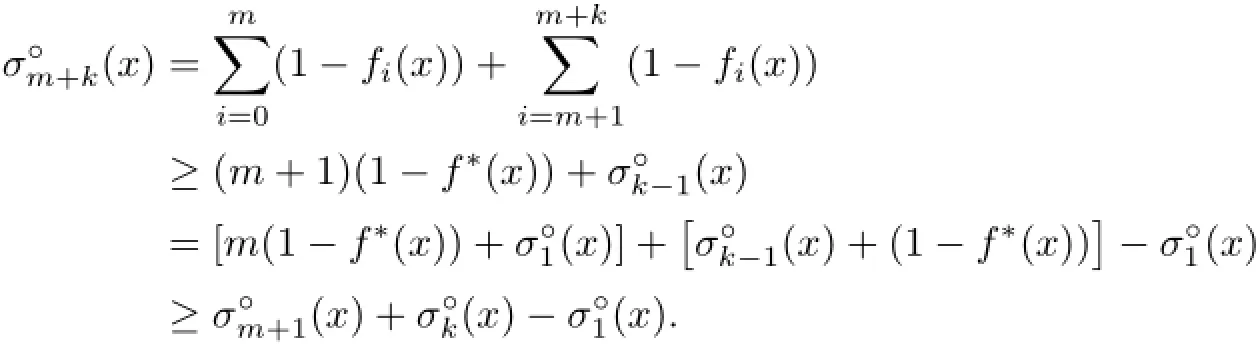
with(not all zeros)αi≥0.Thus，we may find (not all zeros)βi≥0(0≤i≤m+k)such that

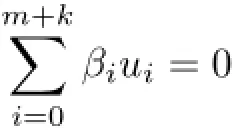
or

Observing that not all βm+1，···，βm+kare zero for otherwiseby Theorem 3.1，and similarly not all β0，···，βmare zero，we have u̸=0.

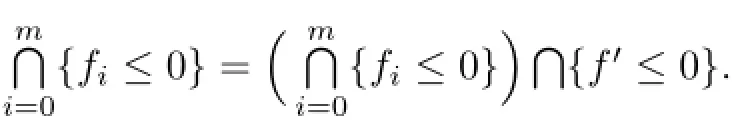
Now，chooseµ＞0 and b∈R such thatSince

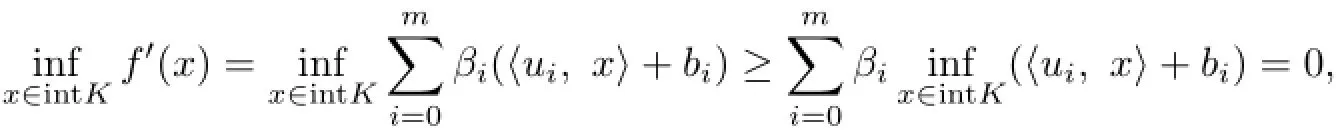
which leads to

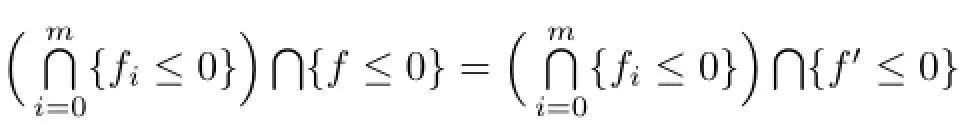
and in turn

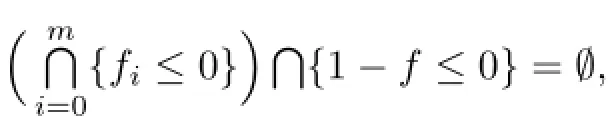
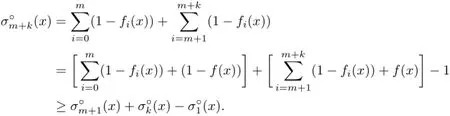
5　Bounds ofin 2 and 3 Dimensional Spaces

In this section，we provide the bounds ofonly for convex bodies in R2and R3.The following lemma is needed.

Theorem 5.1Let K∈K3.Thenfor all m≥1.Moreover，if m≥2， thenfor some x∈intK if and only if K is symmetric w.r.t.x；(x)=1 for some x∈intK if and only if m≤3 and K has an m-simplicial orthogonal projection，i.e.，there is an m-dimensional linear subspace H⊂R3such that PH(K)is an m-simplex，where PHdenotes the orthogonal project from R3to H.

Proof.We may assume m≥2 since σ1≡1，and so there is nothing to discuss，and we discuss the right-hand inequality first.As usual，we write fi(·)=⟨ui，·⟩+bi.

For any x∈intK，letting{f0，···，fm}be a minimizer w.r.t.x，we have clearly

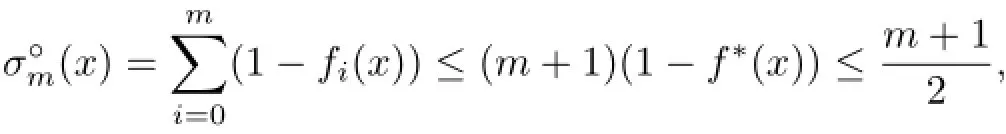
where f∗is the same as in Theorem 4.1(observing that).

If K is symmetric w.r.t.x∈intK，thenfor alland so

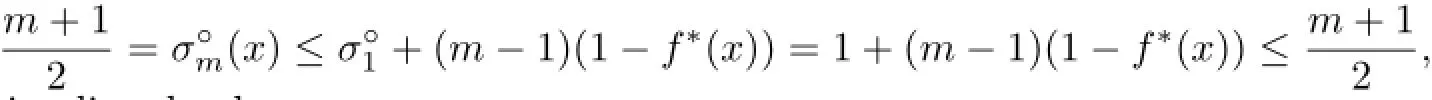
which implies clearly

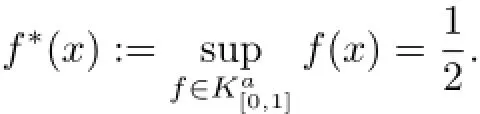
Thus，K is symmetric w.r.t.x.

Now，we discuss the left-hand inequality and start withfirst.

If{f0，f1，f2}∈，then an elementary geometrical discussion shows that either(at least) two of{fi=0}(0≤i≤2)are parallel oris a 2-simplex. For the first case，saying，we have f1=1-f0，and so

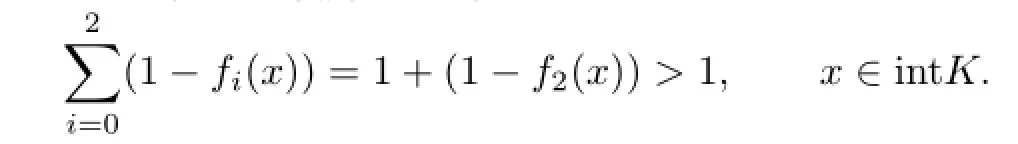
As for the second case，by Lemma 5.1 we have

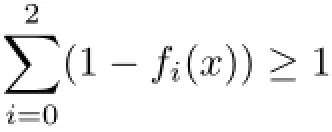
Now，since，by Theorem 4.2，

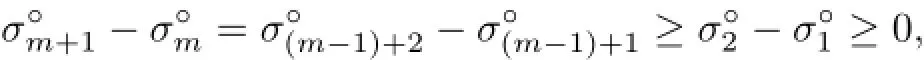
For the equality case，we show first that iffor some x∈intK，then m≤3. In fact，if m＞3，letbe a minimizer w.r.t.x.Then，by Helly’s Lemma， we have，say，，from which we get

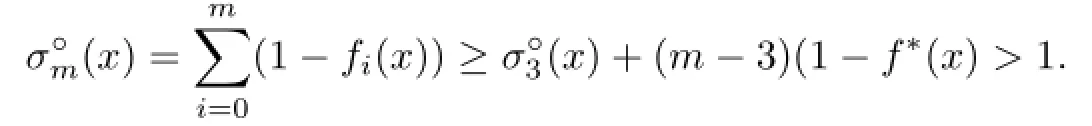
Suppose m=2.If K has a 2-simplex orthogonal projection，i.e.，PH(K)is a 2-simplex in the 2-dimensional subspace H，let(0≤i≤2)be the same as in Lemma 5.1 and in turn let.Then，and

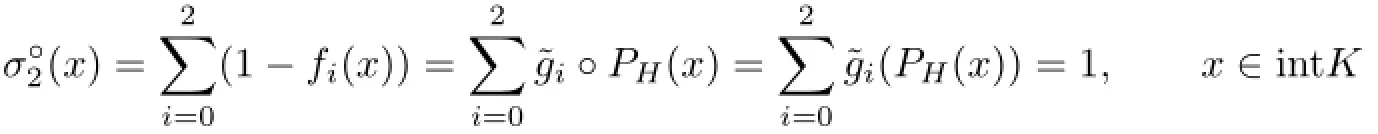
The argument for the case m=3 is the same as the case m=2.This completes the proof.

The same conclusions as those in Theorem 5.1 hold for K∈K2as well with a similar and even simpler argument.

References

[1]Gr¨unbaum B.Measure of symmetry of convex sets.Amer.Math.Soc.，1963，VII:233–270.

[2]Guo Q，Kaijser S.On asymmetry of some convex bodies.Discrete Comput.Geom.，2002，27: 239–247.

[3]Guo Q，Kaijser S.Approximation of convex bodies by convex bodies.Northeast.Math.J.，2003，19:323–332.

[4]Guo Q.Stability of the Minkowski measure of asymmetry for convex bodies.Discrete Comput. Geom.，2005，34:351–362.

[5]Guo Q.On p-measure of asymmetry for convex bodies.Adv.Geom.，2012，12:287–301.

[6]Toth G.Simplicial intersections of a convex set and moduli for spherical minimal immersions. Michigan Math.J.，2004，52(2):341–359.

[7]Toth G.On the shape of the moduli of spherical minimal immersions.Trans.Amer.Math. Soc.，2006，358(6):2425–2446.

[8]Toth G.On the structure of convex sets with applications to the moduli of spherical minimal immersions.Beitr¨age Algebra Geom.，2008，49(2):491–515.

[9]Toth G.On the structure of convex sets with symmetries.Geom.Dedicata，2009，143:69–80.

[10]Toth G.A measure of symmetry for the moduli of spherical minimal immersions.Geom. Dedicata，2012，160:1–14.

[11]Schneider R.Convex Bodies:the Brunn Minkowski Theory.Cambridge:Cambridge University Press，2014.

[12]Hiriart-Urruty J B，Lemar´echal C.Fundamentals of Convex Analysis.Berlin:Springer-Verlag，2001.

10.13447/j.1674-5647.2016.03.03

date:March 11，2015.

The NSF(11271282，11371013)of China and the Graduate Innovation Fund of USTS.

*Corresponding author.

E-mail address:yaodan1210@sina.com(Yao D)，guoqi@mail.usts.edu.cn(Guo Q).