Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching

Shao Dian-guo

(1.School of Mathematics，Jilin University，Changchun，130012)

(2.School of Science，Northeast Dianli University，Jilin City，Jilin，132012)

Communicated by Li Yong



Stochastic Maximum Principle for Optimal Control of Forward-backward Stochastic Pantograph Systems with Regime Switching

Shao Dian-guo1，2

(1.School of Mathematics，Jilin University，Changchun，130012)

(2.School of Science，Northeast Dianli University，Jilin City，Jilin，132012)

Communicated by Li Yong

In this paper，we derive the stochastic maximum principle for optimal control problems of the forward-backward Markovian regime-switching system.The control system is described by an anticipated forward-backward stochastic pantograph equation and modulated by a continuous-time finite-state Markov chain.By virtue of classical variational approach，duality method，and convex analysis，we obtain a stochastic maximum principle for the optimal control.

stochastic control，stochastic maximum principle，anticipated forwardbackward stochastic pantograph equation，variational approach，regime switching，Markov chain

2010 MR subject classification:93E20，49K45，60H10

Document code:A

Article ID:1674-5647(2016)03-0217-12

1　Introduction

It is well known that stochastic optimal control problem plays an important role in control theory.Since 1970’s，many scholars committed to obtaining the maximum principle for the stochastic control system such as Kushner[1]，Bismut[2]–[4]，Bensoussan[5]–[6]，etc.，and acquired very important achievement.The general stochastic maximum principle was obtained by Peng[7]by introducing the second order adjoint equations，which allowed the control enter in both the drift and diffusion coefficients while the control domain was nonconvex.This groundbreaking work makes the stochastic optimal control problem has beenvigorous development.

Stochastic delay differential equations(SDDEs)have come to play an important role in many branches of science and industry.Such models have been used with great success in a variety of application areas，including biology，epidemiology，mechanics，economics and finance.Recently，as a special case of SDDEs，the following stochastic pantograph equations (SPEs)has been received a great deal of attention(see[8]).

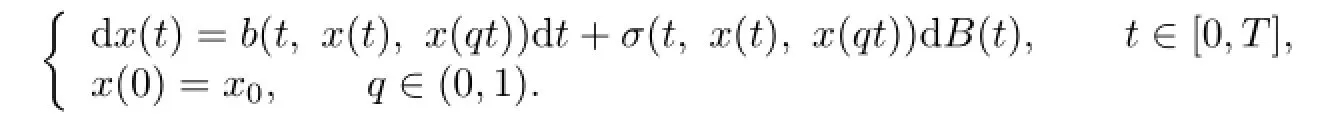
Bismut[2]introduced the linear backward stochastic differential equations(BSDEs).Pardoux and Peng[9]proved the existence and uniqueness for the solution of the nonlinear BSDEs. The applications of a regime-switching model in finance and stochastic control have received significant attention in recent years.The regime-switching model in economic and finance fields was first introduced by Hamilton[10]to describe a time series model and then intensively investigated in the past two decades in mathematical finance.Dokuchaev and Zhou[11]studied a kind of maximum principle when the system dynamics were controlled BSDEs. Then，the forward-backward maximum principle was generalized and applied in finance.We introduce a new type of BSDE，called the anticipated BSDE with Markov chains，as our adjoint equation as follows:

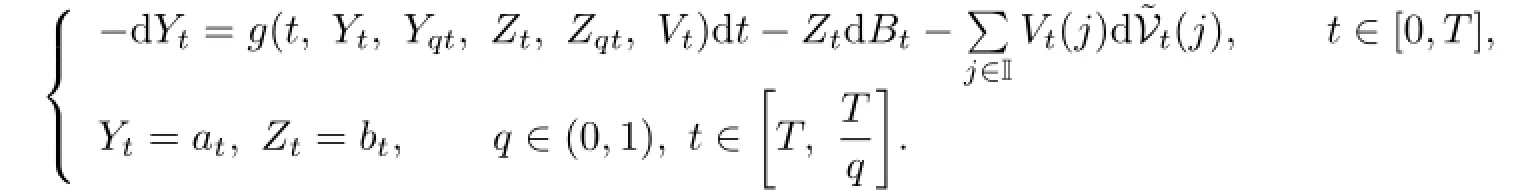
In this paper，by using the results about BSDEs with Markov chains in[12]–[14]，we derive maximum principle for the forward-backward regimes-witching model.To the authors’knowledge，it is the first time to investigate this system.

We sketch out the organization of the paper.In Section 2，we give the preliminaries about anticipated BSDEs with Markov chain and formulates our optimal control problems. We derive the stochastic maximum principle for the optimal control by virtue of the duality method and convex analysis in Section 3.

2　Preliminaries and Formulation of the Optimal Control Problems

2.1Preliminaries

Let(Ω，F，P)be a probability space.T＞0 is a finite-time horizon.{Bt}0≤t≤Tis a ddimensional Brownian motion and{αt}0≤t≤Tis a finite-state Markov chain with the state space given by I={1，2，···，k}.Assume that B and α are independent.The transition intensities are λ(i，j)forwith λ(i，j)non-negative，uniformly bounded，and λ(i，j)=

Let{Ft}0≤t≤Tbe the filtration generated by{Bt，αt}0≤t≤Tand augmented by all P-null sets of F.

Now，we recall some preliminary results about the integer random measure related to the Markov chain(see[12]–[14])；more details about the general integer random measure can be found in Jacod and Shiryaev[15].The auxiliary measured space is(I，BI，ρ)，where I is the state space of Markov chain αt，BIis the sigma field of I，ρ is a nonnegative σ-finite measure on(I，BI)，and defined by ρ(dj)=1 for j∈I.Define V as the integer-valued random measure on，which counts the jumps Vt(j)from any state in I to state j between time 0 and t.Denotewhere P is the predictable sigma field on Ω×[0，T].The compensator of Vt(j)iswhich meansdt is a martingale(compensated measure).Then canonical special semimartingale representation for αtis given by

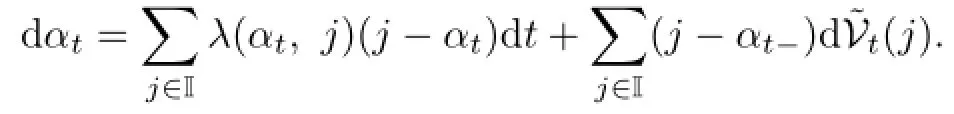
We denote

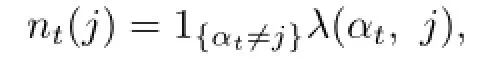
and make the following notations:

Mρ(I；R)，the set of measurable function from(I，BI，ρ)to R，endowed with the topology of convergence in measure.

For w∈Mρ(I；R)，define

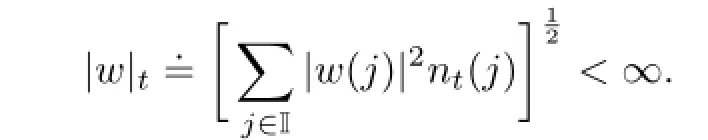
Let|·|denote the Euclidean norm in Rd，the inner product is denoted by

Let L2(FT；Rd)denote the space of Rd-valued FT-measurable random variable ξ，s.t.

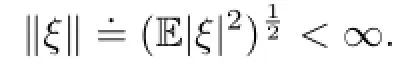
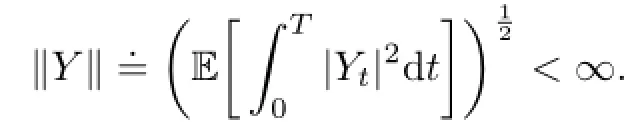
Let L2(；R)denote the space of-measurable functions

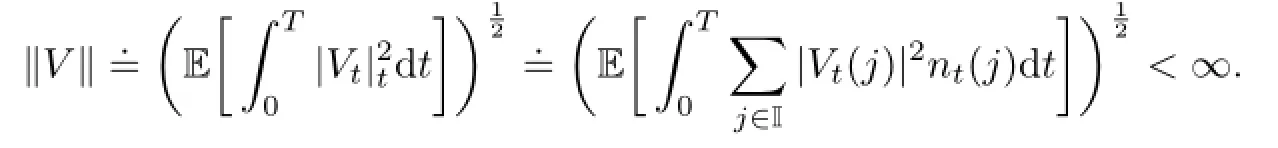
2.2Formulation of the Optimal Control Problems

We consider the following anticipated forward-backward stochastic pantograph systems with regime switching:

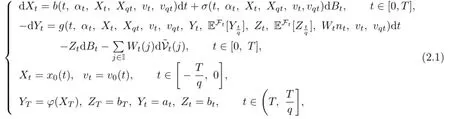
where q∈(0，1)，Wtnt.=(Wt(1)nt(1)，···，Wt(k)nt(k))and x0(t)，v0(t)are deterministic functions.Furthermore，

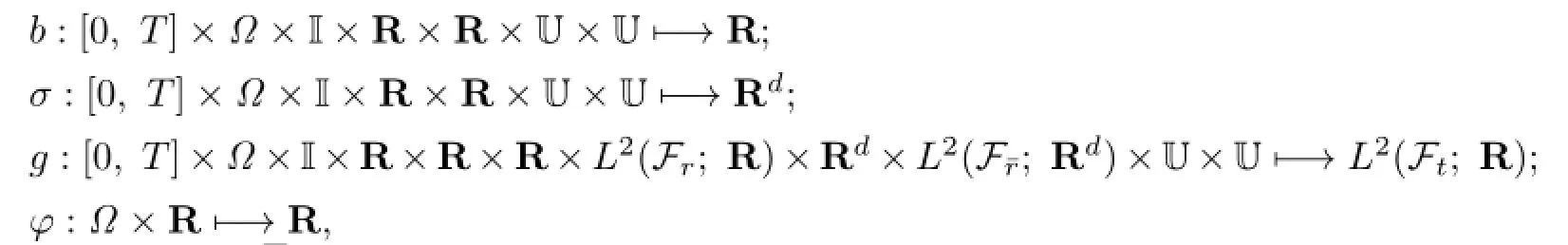
In the aforementioned section，vtis an Ft-adapted stochastic control with values in U，and U⊂R is a non-empty，convex set.Denote by U the class of admissible control taking values in the convex domain U and satisfying

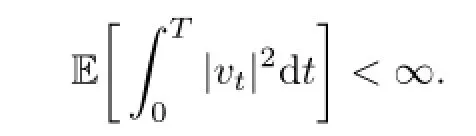
We can define the following cost functional:

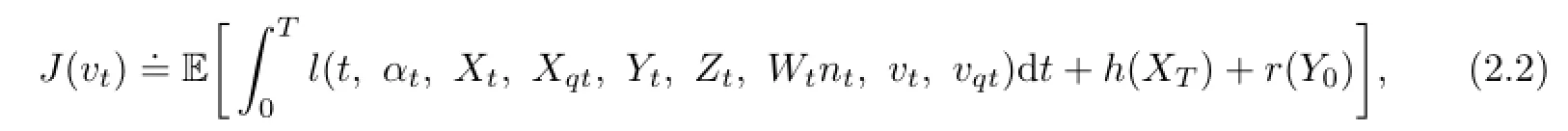
where l，h，r are measurable functions.Throughout this paper，for notational simplicity，we only consider the case where Xtand Ytare 1-dimensional processes，and we denote Xqt，， vqtby Xq，Y¯q，vq，respectively.Let us impose some assumption conditions on the coefficients of the optimal control problem.

Assumption 2.1(i)b，σ，g，φ，l，h and r are all continuous differentiable with respect to the variables(x，xq，y，yq，z，zq，w，v，vq).

(ii)The derivatives of b，σ，g and φ are bounded by C(1+|x|+|xq|+|y|+|z|+|w|+ |v|+|vq|)，where C＞0 is a constant..

(iii)The derivatives of l，h and r are bounded by C(1+|x|+|xq|+|y|+|z|+|w|+|v|+|vq|)，C(1+|x|)，C(1+|y|)respectively，where C＞0 is a constant.

Remark 2.1The derivatives of θ with respect to(x，xq，y，yq，z，zq，w，v，vq)are denoted by θx，θxq，θy，θyq，θz，θzq，θw(j)，j∈I，θv，θvq，respectively，where θ=b，σ，g，h.

By Assumption 2.1，there exists a uniqueness solution forBecause ntis uniformly bounded，we have

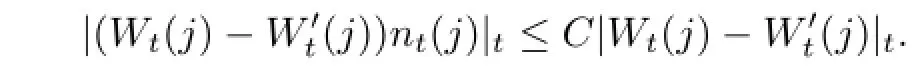
Due to the aforementioned fact and Assumption 2.1，it is easy to check that g in the control system satisfies the Lipschitz condition for(y，yq，z，zq，w)，which guarantees the unique solution infor the BSDE.The objective of our optimal control problem is to maximize the cost functional(2.2)over the admissible control set U.The control ut，which maximizes(2.2)，is called the optimal control.

3　Stochastic Maximum Principle for Optimal Control

In this section，we derive the stochastic maximum principle for the optimal control problems in Section 2 by the classic convex variation method.

3.1Maximum Principle

Let utbe an optimal control for the control problem(2.1)，the corresponding trajectory is denoted by(Xt，Yt，Zt，Wt).Letbe another adapted control process，satisfyingFor the reason that the control domain U is convex，we have for 0≤ρ≤1，Its corresponding trajectory is denoted by

For notational simplicity，we denote:

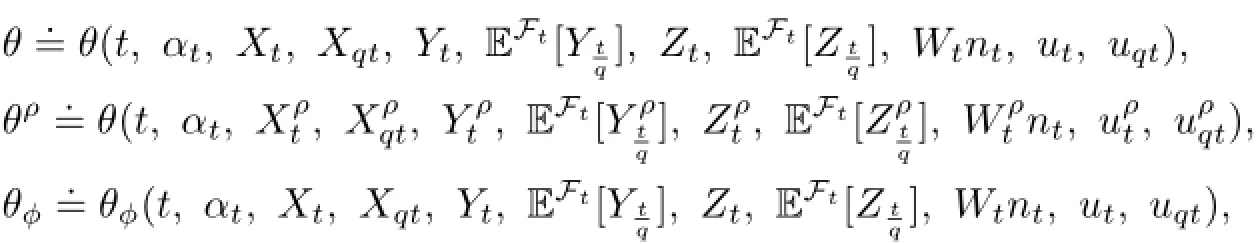
where θ=b，σ，g，l，and ϕ=x，xq，y，yq，z，zq，w(j)，j∈I，v，vq.

We introduce the following variational equation，which is a linear anticipated forwardbackward stochastic pantograph equation with Markov chain:

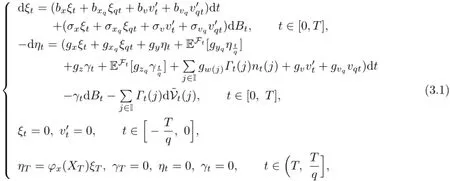
where q∈(0，1).

Obviously，(3.1)has a unique solution(ξt，ηt，γt，Γt)

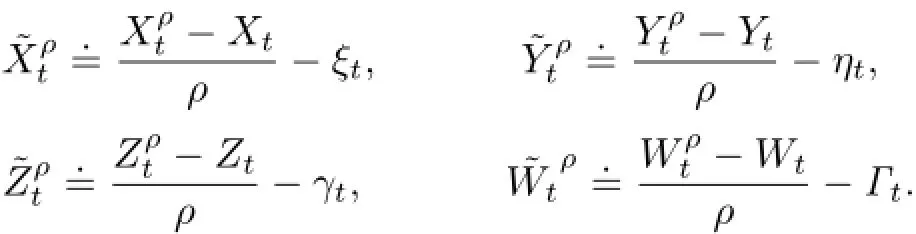
We have the following convergence results.

Lemma 3.1Suppose that Assumption 2.1 holds.Then

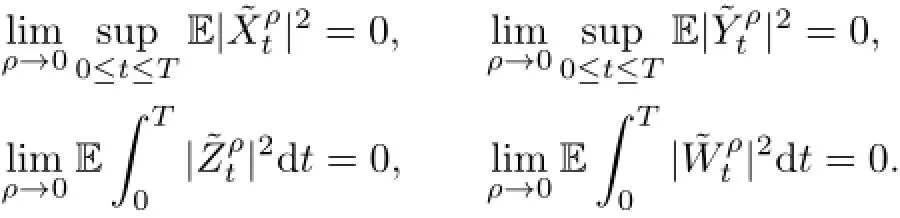
Proof.The first convergence foris similar to(3.1)in[5]，so we omit it.We prove the other three convergences.By the definition of，we have

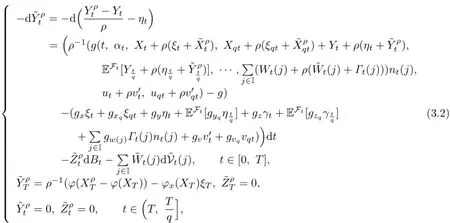
where q∈(0，1).

Let

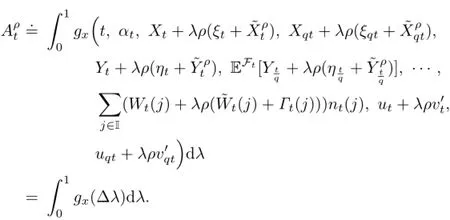
Similarly，

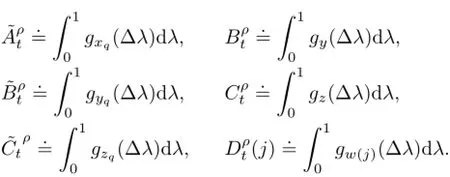
Due to Assumption 2.1，they are all bounded.

We also denote

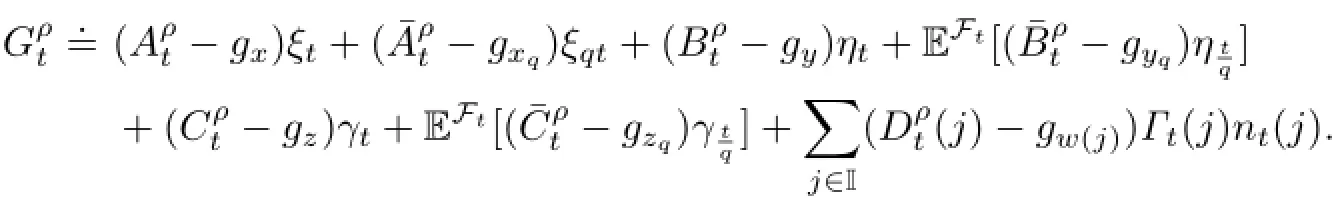
Obviously，we have

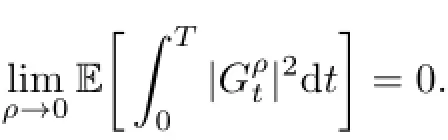
Then we can rewrite(3.2)as follows:

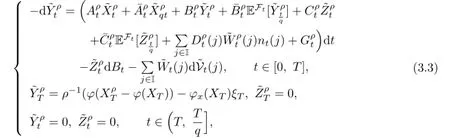
where q∈(0，1).

Notice that the predictable covariation of(j)is

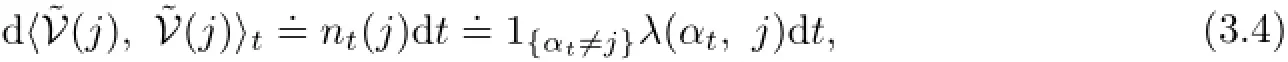
and we have

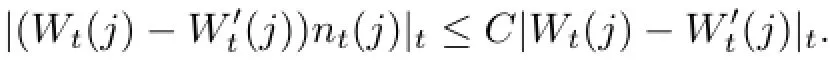
By using it and(3.4)，applying the integration by parts to，we can obtain

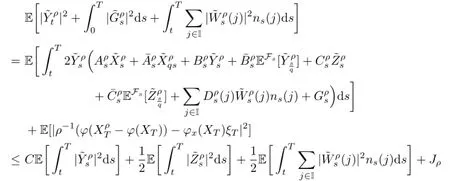
with

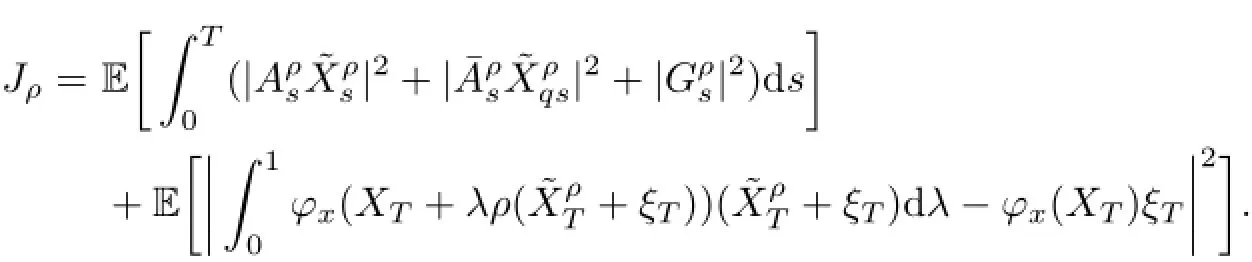
We have

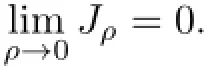
Applying Gronwall’s inequality，we can prove the last three convergence results.The proof is completed.

Since utis an optimal control，we have

Then we can prove the following variational inequality.

Lemma 3.2Under the Assumption 2.1，the following variational inequality holds:

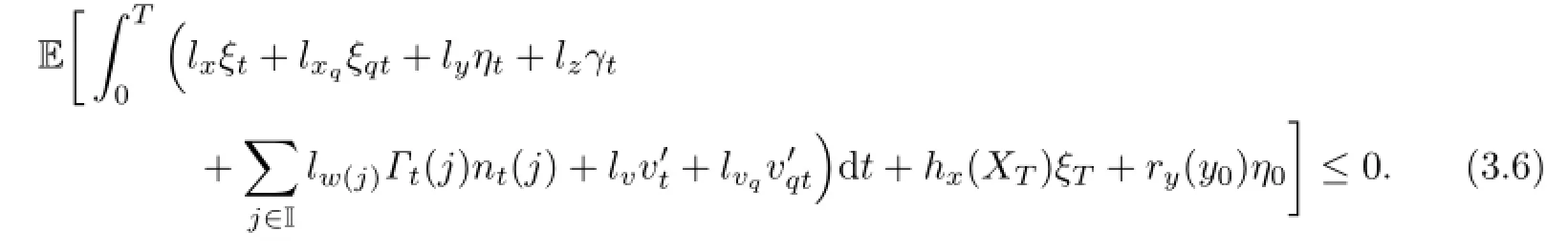
Proof.From the convergence results in Lemma 3.1，we have

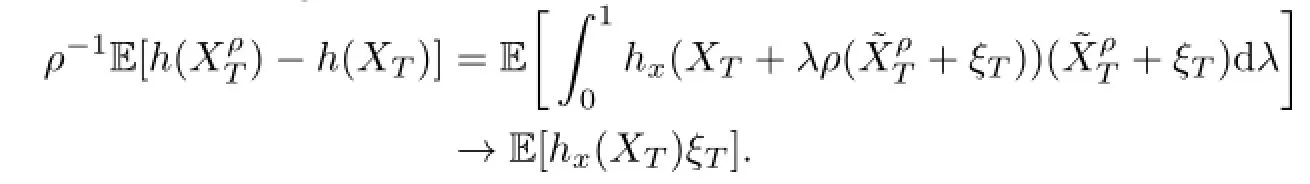
Similarly，we have

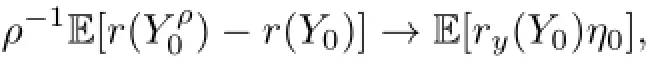
and

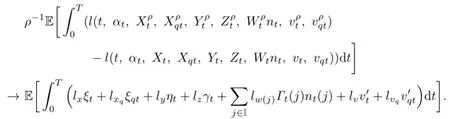
Then(3.6)follows from(3.5).The proof is completed.

For deriving the maximum principle，we introduce the following adjoint equation:

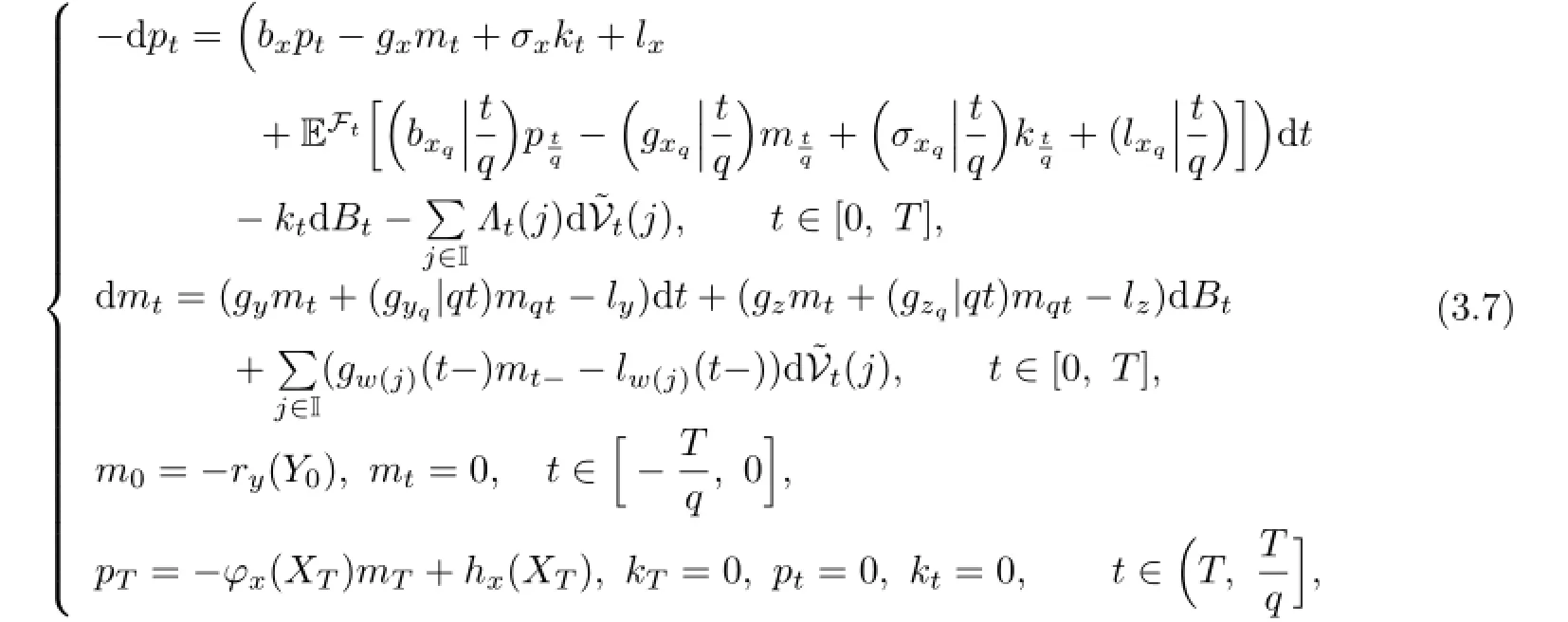
where q∈(0，1)，gwj(t-)，lw(j)(t-)are defined by

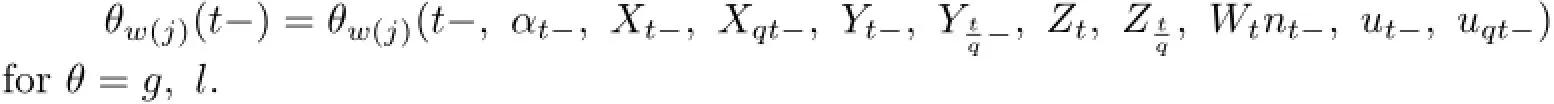
xqwe use the same notation for σ，g，l.(gyq|qt)，(gzq|qt)denote the value of gyq，gzq，when time t takes value qt.

From Assumption 2.1，we can see that(3.7)has a unique solution(mt，pt，kt，Λt) inTo establish a maximum principle for the optimal control problem，we define a Hamiltonian function H:as follows:

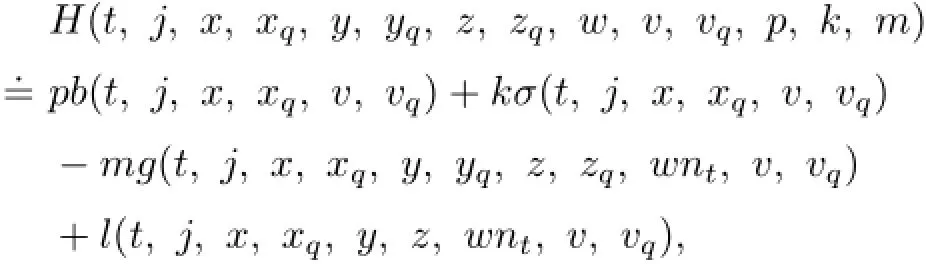
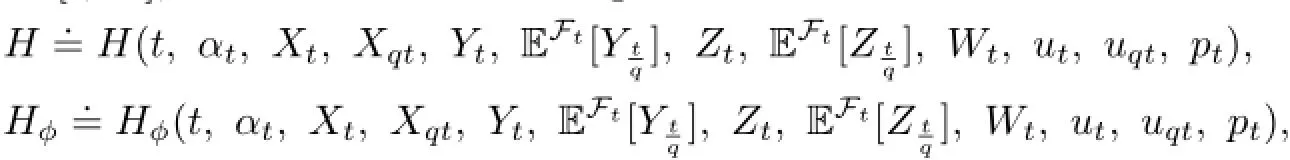
where ϕ=x，xq，y，yq，z，zq，w(j)，j∈I，v，vq.By using this notation，we can rewrite the adjoint equations(3.7)as the following Hamilton system:

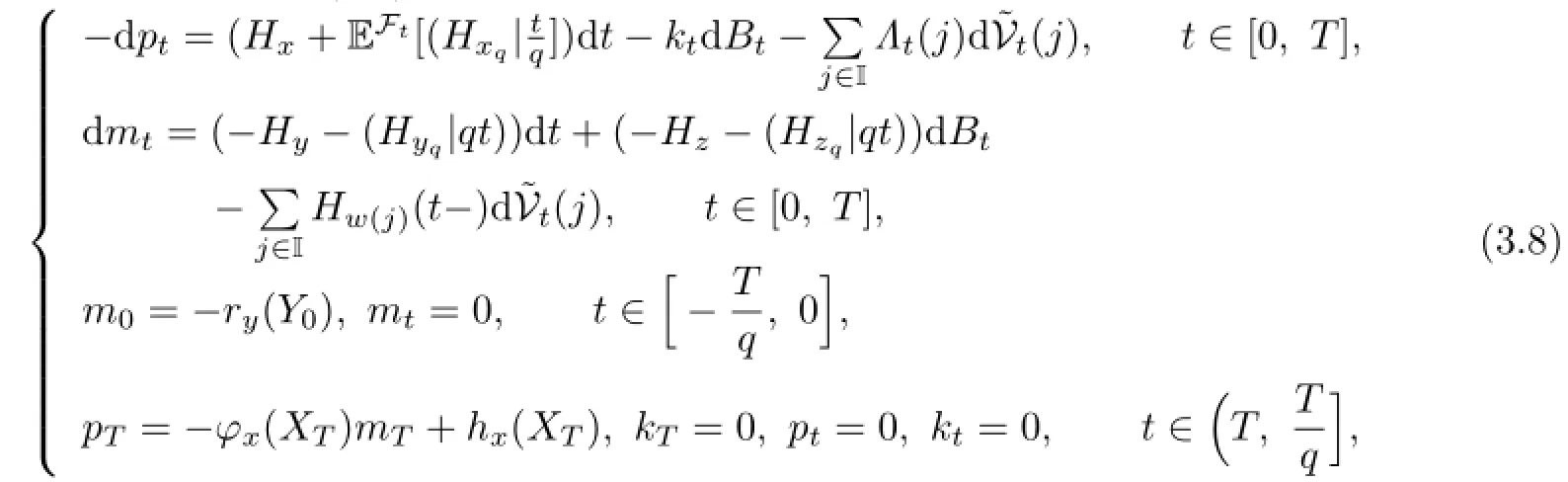
where q∈(0，1).

Now we can obtain the stochastic maximum principle.

Theorem 3.1(Maximum Principle)Let utbe an optimal control，(Xt，Yt，Zt，Wt)be the corresponding trajectory，and(mt，pt，kt，Λt)be the unique solution of adjoint equation (3.7)or(3.8).Then，for any v∈U，we have

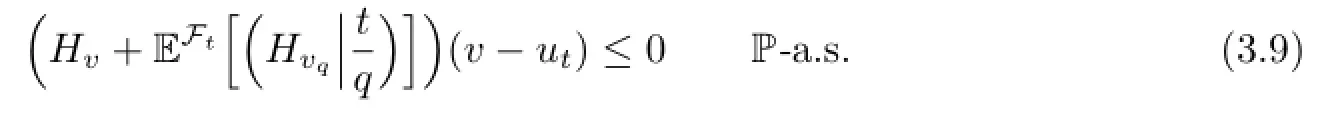
Proof.By using Itˆo’s formula by parts to ptξt+mtηt，we have

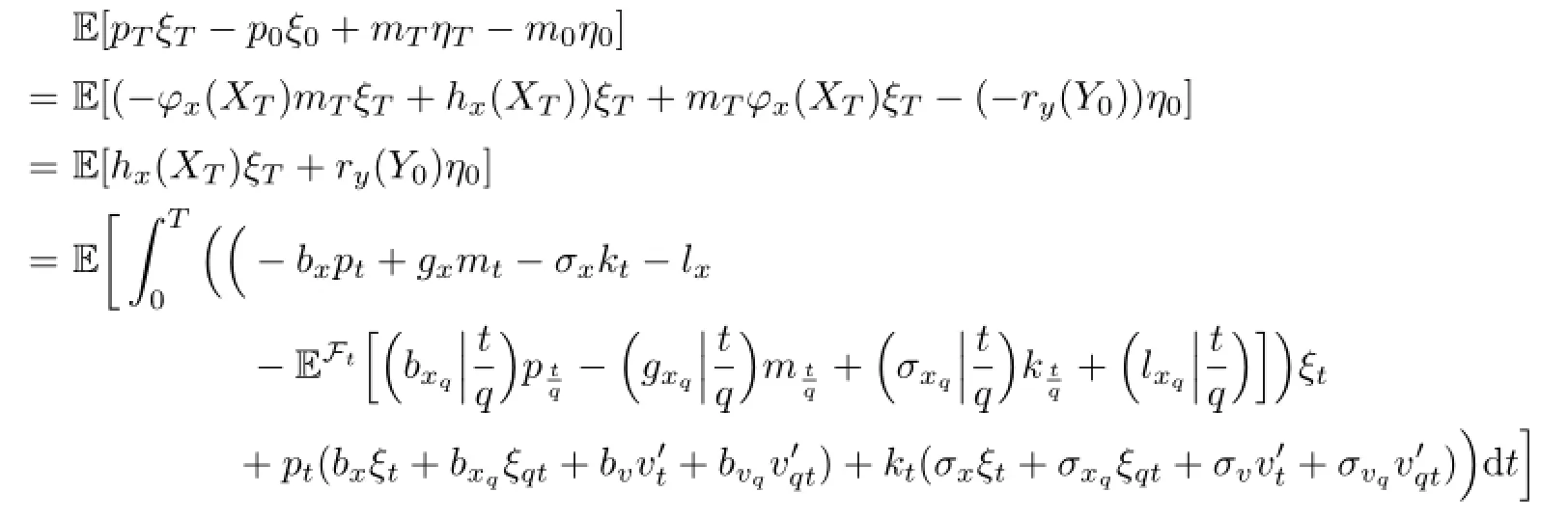
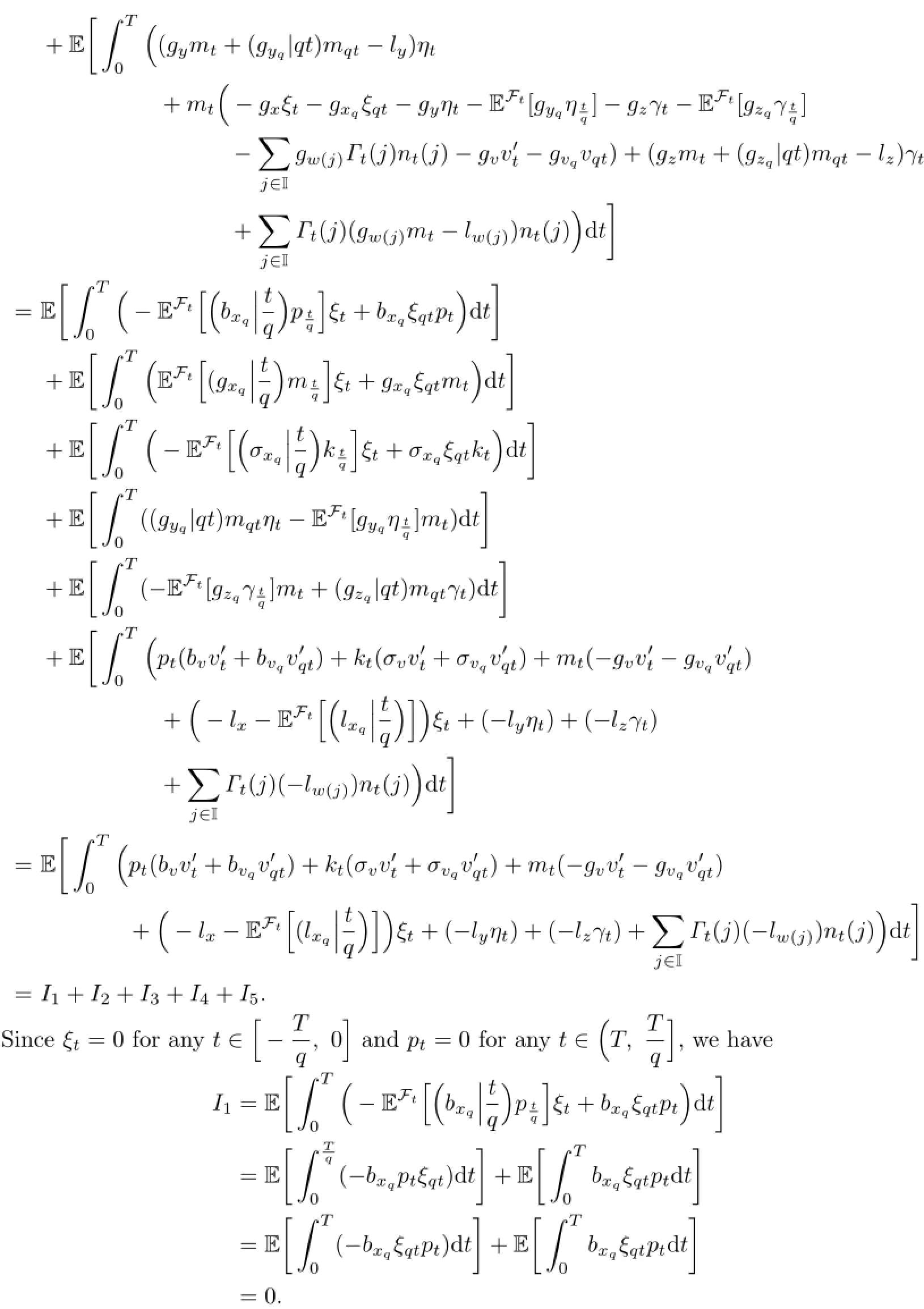
Similarly，we have I2=I3=0.

On the other hand，since ηt=0 for anyand mt=0 for any

we have

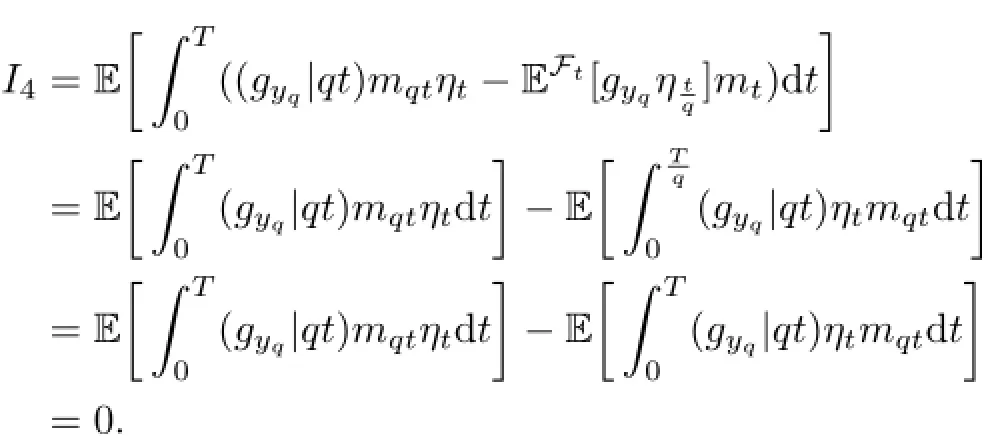
Similarly，we have I5=0.

Then，by the variational inequality(3.6)，we have

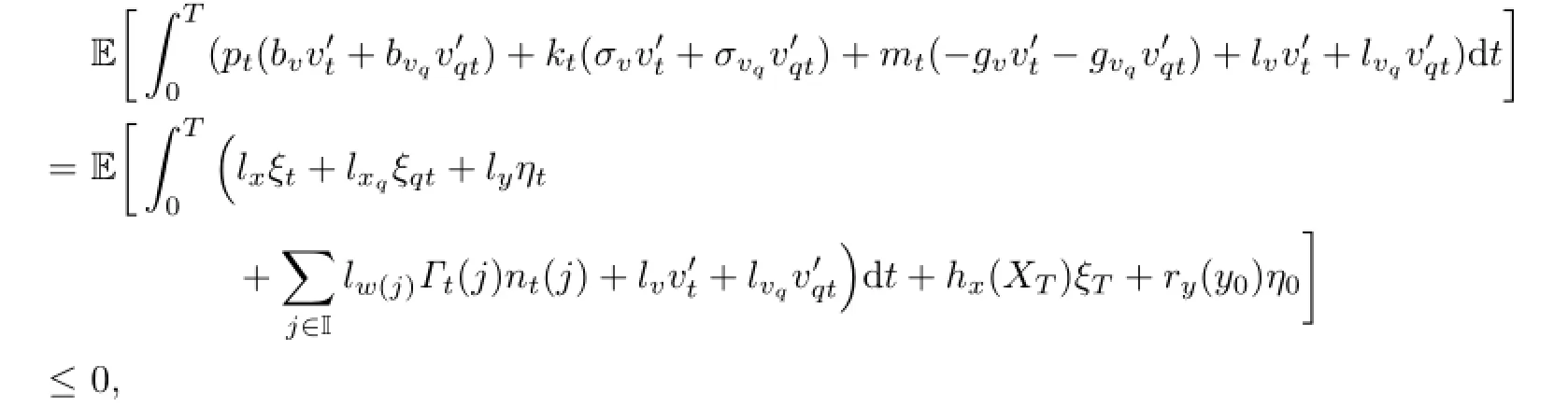
or

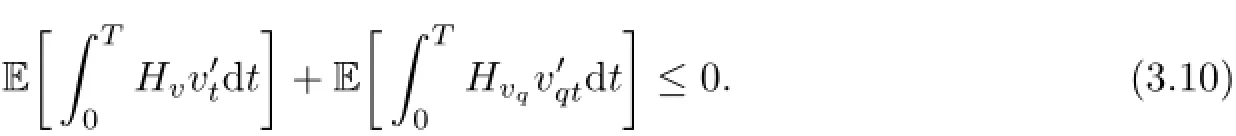
Let us+be of the following form:

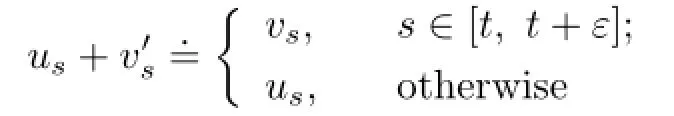
for arbitrary vs∈U.Then(3.10)leads to

or

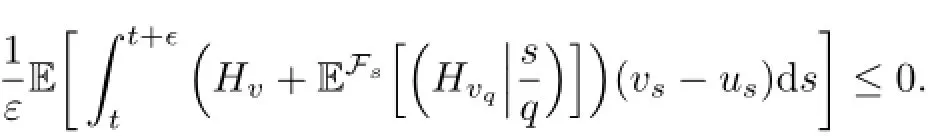
By letting ε→0，we obtain

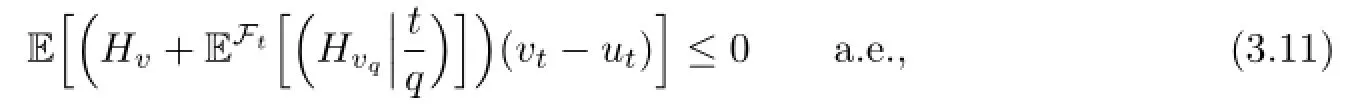
for any admissible control vt.

Let ωt=v1A+ut1ACfor A∈Ftand v∈U.Obviously，ωtis an admissible control. Applying the inequality(3.11)with ωt，we can get

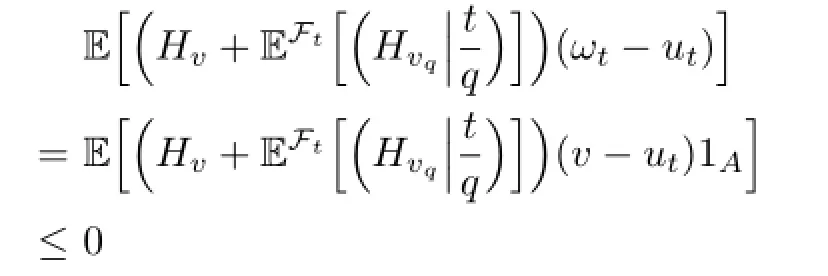
for all A∈Ft.This implies

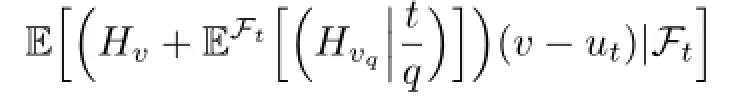
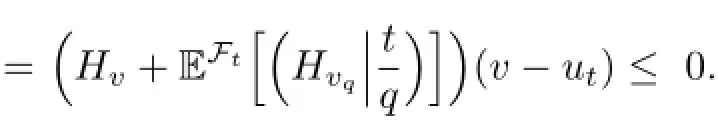
Our proof is completed.

Remark 3.2The maximum principle(3.9)implies that

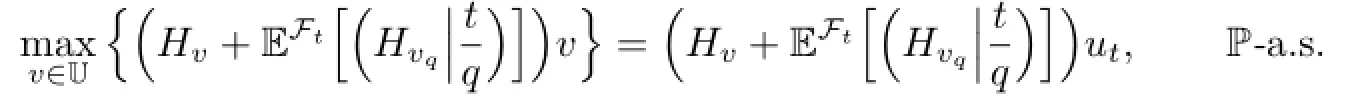
4　Conclusion

Inspired by some interesting economical and financial phenomena still unexplained by theories，we study a kind of stochastic optimal control problem of anticipated forward-backward stochastic pantograph systems with regime switching.Specifically，we establish a stochastic maximum principle for the optimal control by virtue of the duality method and convex analysis.

References

[1]Kushner H J.Necessary conditions for continuous parameter stochastic optimization problems. SIAM J.Control，1972，10:550–565.

[2]Bismut J M.Conjugate convex functions in optimal stochastic control.J.Math.Anal.Appl.，1973，44:384–404.

[3]Bismut J M.Th´eorie probabiliste du contrˆole des diffusions.Mem.Amer.Math.Soc.，1976，4(167):130pp.

[4]Bismut J M.An introductory approach to duality in optimal stochastic control.SIAM Rev.，1978，20(1):62–78.

[5]Bensoussan A.Lectures on Stochastic Control.in:Lecture Notes in Mathematics，972.Berlin: Springer-Verlag，1982.

[6]Bensoussan A.Stochastic maximum principle for distributed parameter system.J.Franklin Inst.，1983，315:387–406.

[7]Peng S.A general stochastic maximum principle for optimal control problems.SIAM J.Control Optim.，1990，28(4):966–979.

[8]Baker C T H，Buckwar E.Continuous θ-methods for the stochastic pantograph equation. Electron.Trans.Numer.Anal.，2000，11:131–151.

[9]Pardoux´E，Peng S.Adapted solution of a backward stochastic differential equation.Systems Control Lett.，1990，14:55–61.

[10]Hamilton J.A new approach to the economic analysis of non-stationary time series.Econometrica，1989，57:357–384.

[11]Dokuchaev N，Zhou X.Stochastic controls with terminal contingent conditions.J.Math.Anal. Appl.，1999，238:143–165.

[12]Cr´epey S.About the pricing equations in finance.in:Paris-Princeton Lectures on Mathematical Finance.Berlin:Springer，2010.

[13]Wang S J，Wu Z.Maximum principle for optimal control problems of forward-backward regime-switching systems involving impulse controls.Math.Probl.Eng.，2015，2015，Article ID 892304，13pp.

[14]Lv S Y，Tao R，Wu Z.Maximum principle for optimal control of anticipated forward-backward stochastic differential delayed systems with regime switching.Optim.Control Appl.Meth.，2016，37:154–175.

[15]Jacod J，Shiryaev A.Limit Theorems for Stochastic Processes，Second edition.in:Grundlehren der Mathematischen Wissenschaften.Berlin:Springer-Verlag，2003.

10.13447/j.1674-5647.2016.03.04

date:March 16，2015.

The NSF(11401089)of China，the Science and Technology Project(20130101065JC)of Jilin Province.

E-mail address:shaodgnedu@163.com(Shao D G).