Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations

Dai Qun，Li Hui-laiand Liu Su-li

(1.College of Science，Changchun University of Science and Technology，Changchun，130022)

(2.School of Mathematics，Jilin University，Changchun，130012)

Communicated by Wang Chun-peng



Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations

Dai Qun1，Li Hui-lai2and Liu Su-li2

(1.College of Science，Changchun University of Science and Technology，Changchun，130022)

(2.School of Mathematics，Jilin University，Changchun，130012)

Communicated by Wang Chun-peng

In this paper，we prove the existence and uniqueness of positive solutions for a system of multi-order fractional differential equations.The system is used to represent constitutive relation for viscoelastic model of fractional differential equations.Our results are based on the fixed point theorems of increasing operator and the cone theory，some illustrative examples are also presented.

fractional differential equation，Caputo fractional derivative，fixed point theorem，positive solution

2010 MR subject classification:34A08，35B44

Document code:A

Article ID:1674-5647(2016)03-0249-10

1　Introduction

In recent years，fractional differential equations arise in many engineering and scientific disciplines as the mathematical modeling of systems and processes in the fields of physics，chemistry，aerodynamics，electrodynamics of complex medium，polymer rheology，economics，blood flow phenomena，etc.，see[1]–[5].

Recently，the existence of solutions to fractional differential equations have been studied by many authors，see[6]–[14].In this paper，we consider the following initial value problem for a system of fractional differential equations:

where L1(D)=DSn-an−1DSn−1-···-a1DS1，0＜α＜S1＜···＜Sn−1＜Sn≤1，ai＞0，L2(D)=DKm-bm−1DKm−1-···-b1DK1，0＜β＜K1＜···＜Km−1＜Km≤1，bj＞0，α≤Km，β≤Sn，DSi，DKj(i=1，2，···，n-1；j=1，2，···，m-1)are the standard Caputo fractional derivatives，and f，g:[0，1]×[0，+∞)→[0，+∞)are continuous.

The system(1.1)is used to represent constitutive relation for viscoelastic model of fractional differential equations.Moreover，the system(1.1)describes processes of heat diffusion and combustion in two-component continua with nonlinear heat conduction and volumetric release.When we take∆u，∆v instead of u，v and let S1=K1=n=m=1，it expresses as macroscopic models II for electrodiffusion of ions in nerve cells when molecular diffusion is anomalous subdiffusion due to binding，crowding or trapping(refer to[9]).

This paper is organized as follows.In Section 2，we present some basic materials needed to prove our main results.In Section 3，we prove the existence and uniqueness of positive solutions for(1.1)by applying the fixed point theorems of increasing operator and the cone theory.

2　Preliminaries

We recall several known definitions and properties from fractional calculus theory(refer to [1]and[15]).

Definition 2.1The Riemann-Liouville fractional integral of a function f:(0，1]→R of order α＞0 is given by

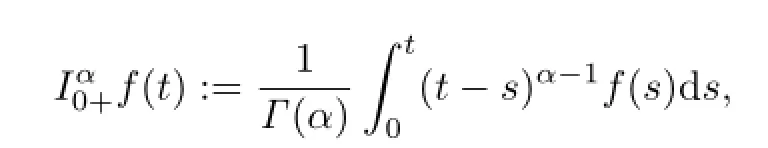
provided that the right-hand side is pointwise defined on(0，1]，and Γ is the gamma function.

Definition 2.2For at least n-times continuously differentiable function f:[0，+∞)→R，the Caputo derivative of order α is defined as

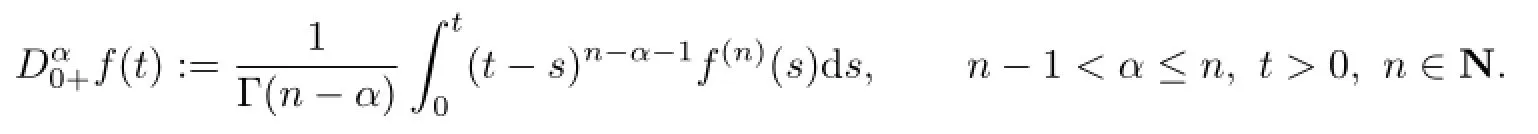
Hereafter Dαdenotesand Iαdenotes.

Definition 2.3A Banach space E endowed with a closed cone K is an ordered Banach space(E，K)with a partial order≤in E as follows:

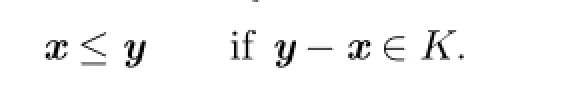
Definition 2.4For x，y∈E，the order interval⟨x，y⟩is defined as

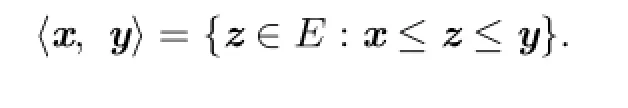
Lemma 2.1Let β＞α＞0，f∈L1[a，b].Then

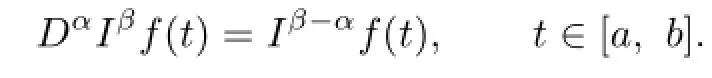
Lemma 2.2Let(E，K)be an ordered Banach space，x0，y0∈K，x0≤y0，F:⟨x0，y0⟩→⟨x0，y0⟩be an increasing operator，and Fx0≥x0，Fy0≤y0.If F is continuous and compact and K is a normal cone，then F has a fixed point which lies in⟨x0，y0⟩.

Lemma 2.3Let(E，K)be an ordered Banach space，U1，U2be open subsets of E withbe completely continuous.Suppose either

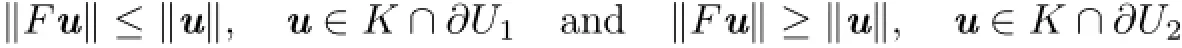
or

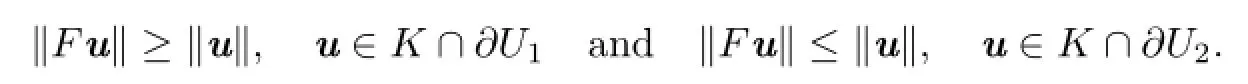
Then F has a fixed point.

Let us introduce the space X={u(t):u(t)∈C1[0，1]}endowed with the norm

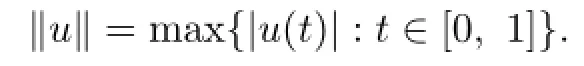
Let

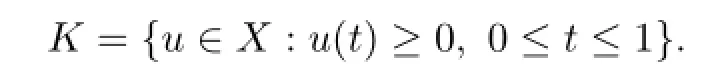
Obviously，K is a normal cone.

3　Main Results

Lemma 3.1Assume that g and f:[0，1]×R→[0，+∞)are continuous.Then(1.1)is equivalent to the following system of integral equations:

Proof.Let

Then in view of(1.1)we find that

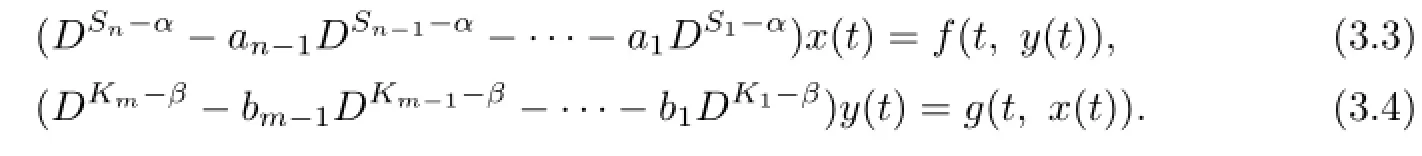
Applying ISn−αto both sides of(3.3)，by Lemma 2.1，we can get

For u(t)=Iαx(t)and the initial value condition u(0)=0.

By(3.5)，we can get(3.1).Similarly，we also have(3.2).

F，G:K→K can be defined as

Lemma 3.2Let M be a bounded subset of K.Then there exists a positive constant l such that for any uare compact sets.

Proof.We only need to verify that F and G:K→K are completely continuous operators. First，we prove that F(M)is a bounded set.

Let

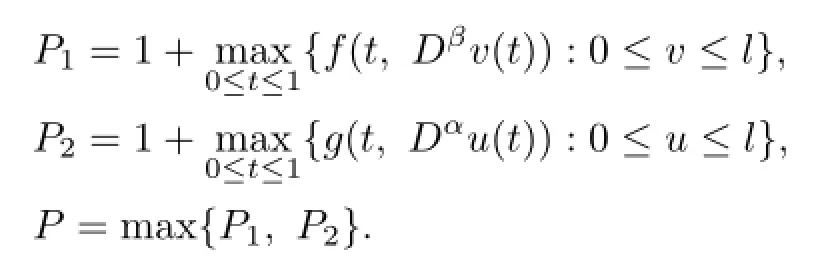
We have

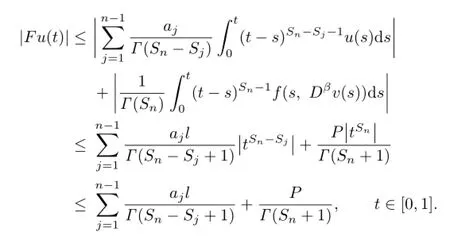
Similarly，we also have

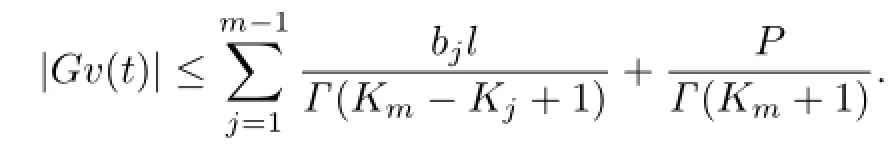
Thus，F(M)and G(M)are bounded sets.

Second，we prove that the operator F is equicontinuous.

Let u∈M，and for any 0≤t1＜t2≤1，|t1-t2|＜δ.Then

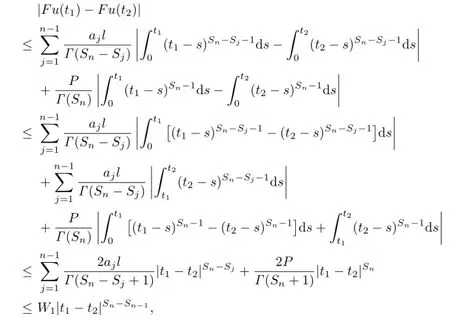
where W1is independent of t1，t2.

Similarly，we also have

where W2is independent of t1，t2.

Thus，F and G are equicontinuous operators.By Arzela-Ascoli Theorem，we know thatandare compact sets.

Theorem 3.1If there exists a constant λ＞0 such thatand there existsuch that

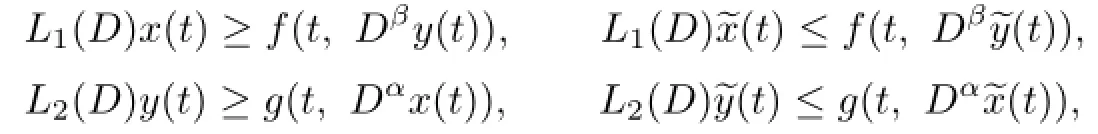
then(1.1)has at least one positive solution.

Proof.We only need to verify that F，G have fixed points.By Lemma 3.2，we know that F and G are completely continuous.For u1＜u2，v1＜v2，u1，u2，v1，v2∈K，we have

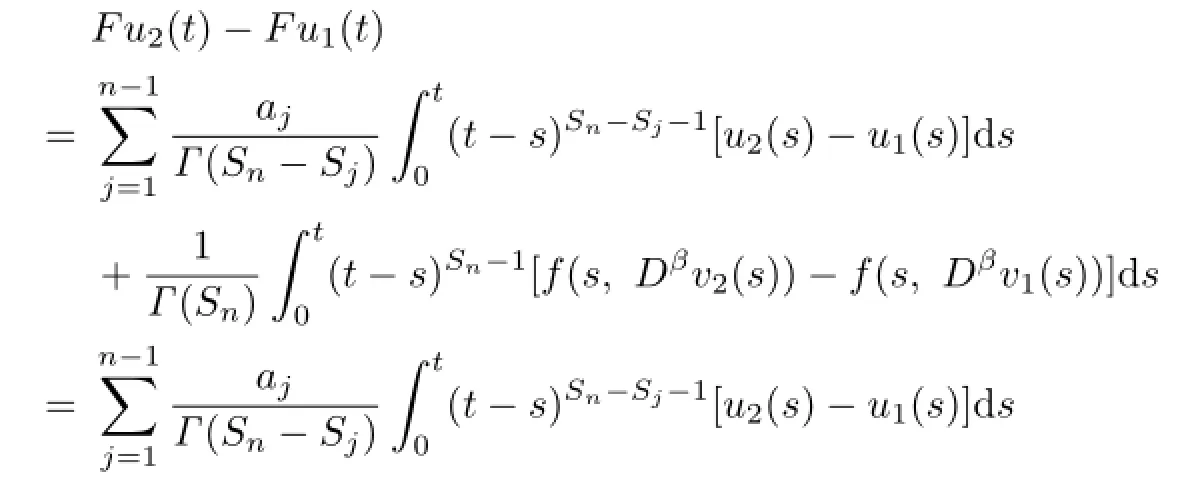
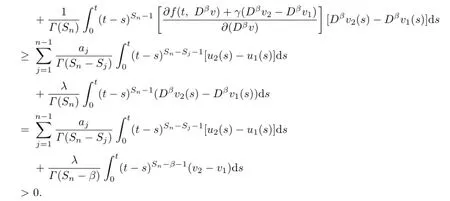
Therefore，

In the same way，we can obtain that

Thus，F and G are increasing operators.

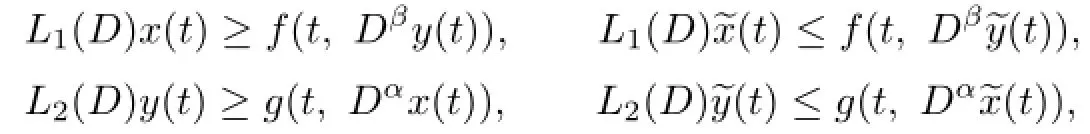
we can get

By Lemma 2.2，F and G have fixed points

Theorem 3.2If there exists a constant λ＞0 such thatand for any t∈[0，1]，

then(1.1)has at least one positive solution.

Proof.There exist N＞0 and R＞0 such that for any|Dβv|≥R and|Dαu|≥R，

Let

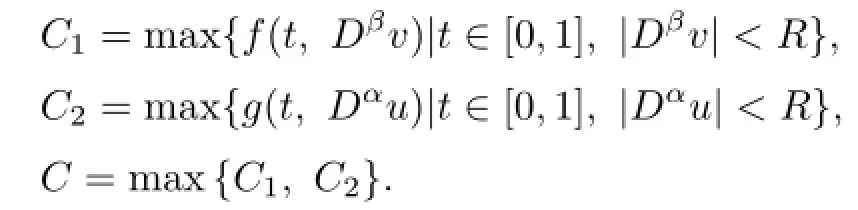
Hence，for any v，u＞0，one has

We consider the following system of fractional differential equations:

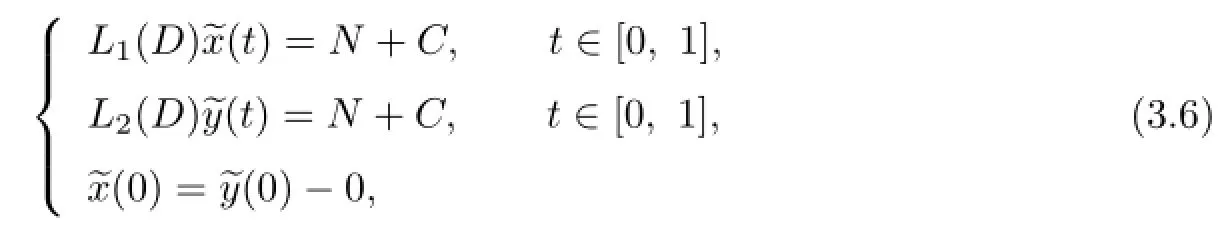
where

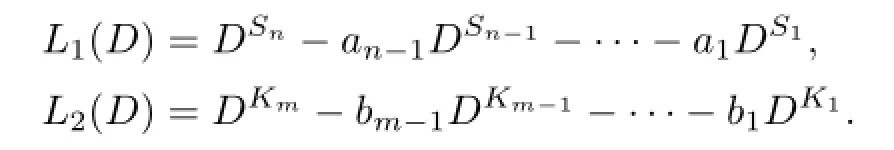
By Lemma 3.1，(3.6)is equivalent to the following integral equations:

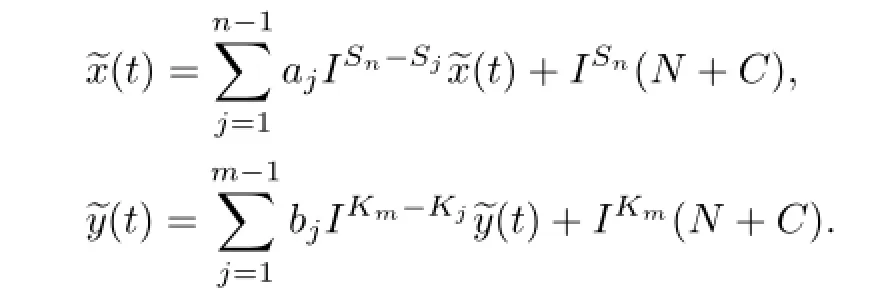
We have

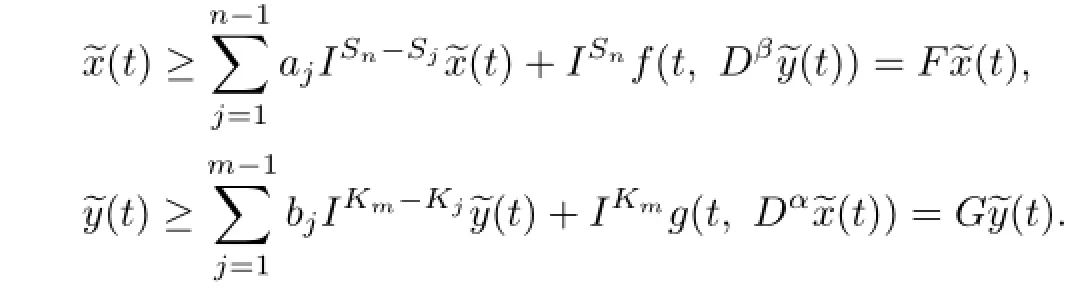
There exist x(t)=y(t)=0 such that

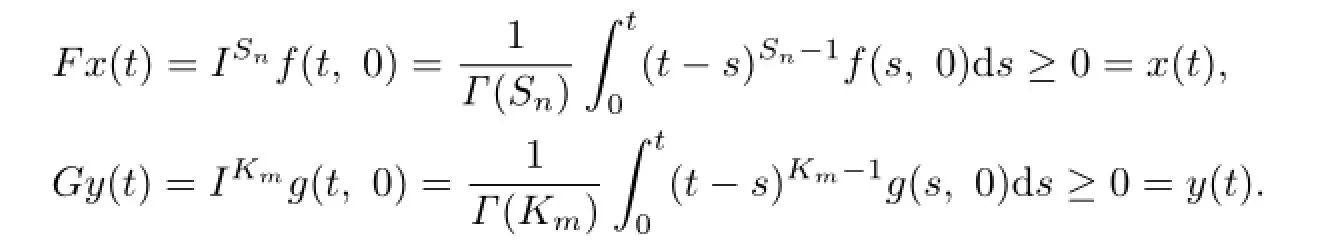
By Theorem 3.1，this completes the proof.

Theorem 3.3Let

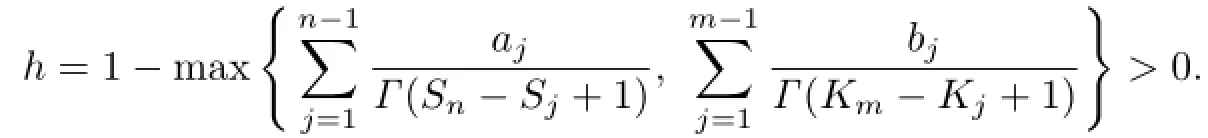
Assume that there exist two distinct positive constantsandsuch that

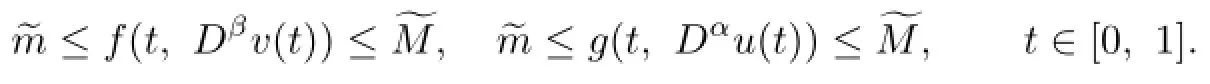
Then(1.1)has at least one positive solution.

Proof.Let

where

For v，u∈K∩∂U2，we have

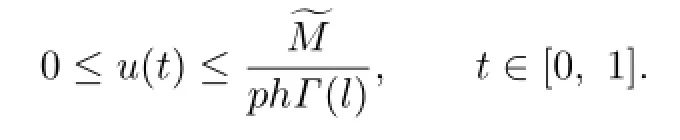
Since f(t，Dβv(t))≤，we have

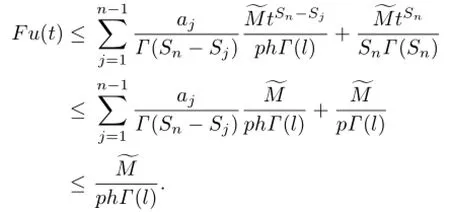
Hence

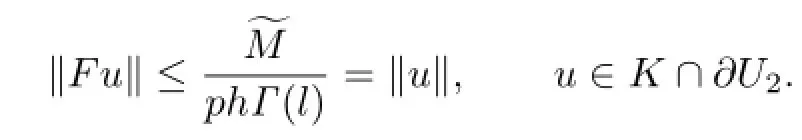
Similarly，we also have

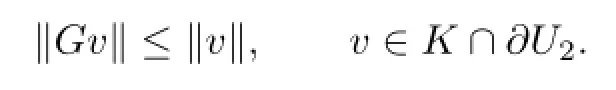
On the other hand，for u∈K∩∂U1，we have

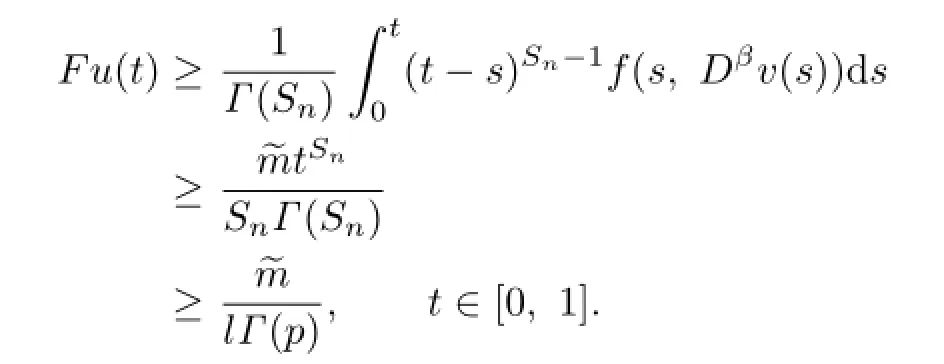
Hence

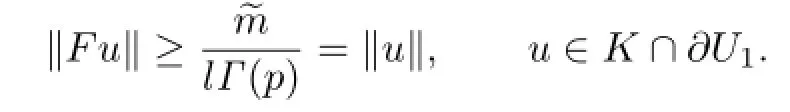
Similarly，we also have

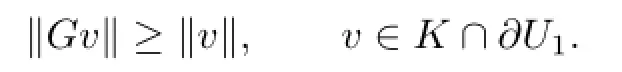
By Lemma 2.3，we know that(1.1)has a fixed point in K∩

Theorem 3.4Assume that there exists a constant M＞0 such that for any t∈[0，1]，f，g satisfy the Lipschitz conditions:

Let

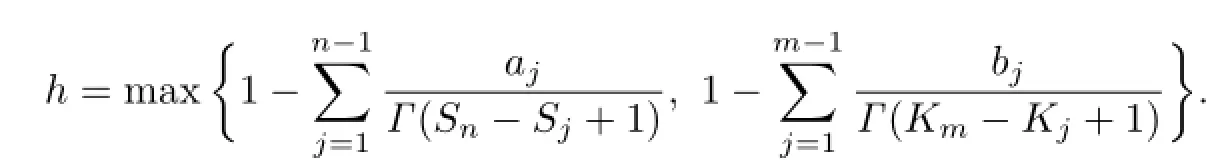
Proof.By Theorem 3.2，we know that(1.1)has at least one positive solution.For u1，u2，v1，v2∈K，we have

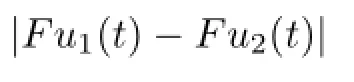
By(3.2)，one has

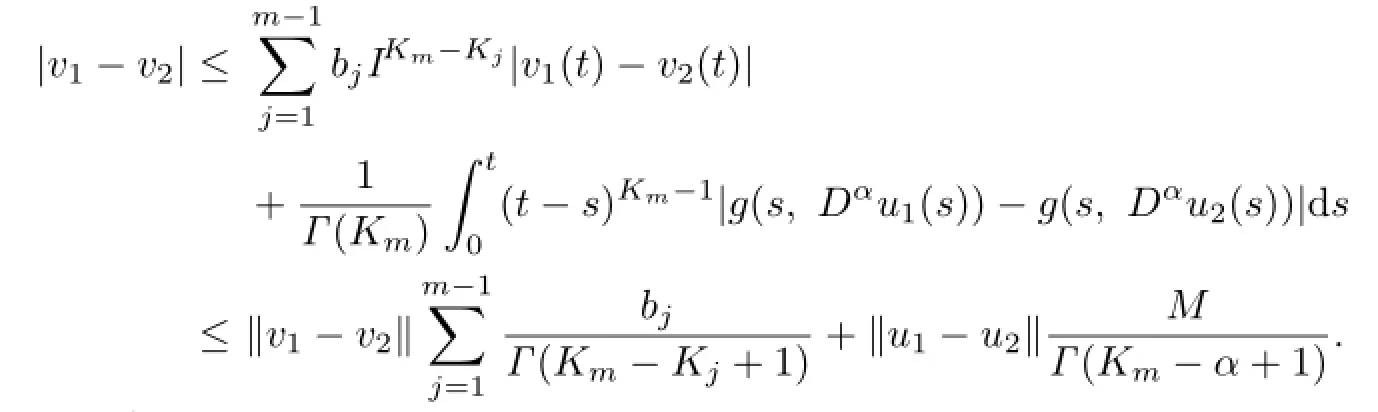
For h＞0，we have

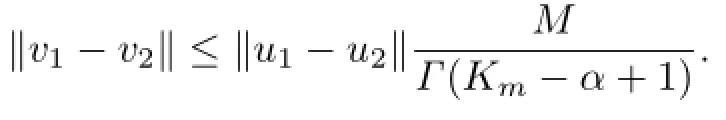
Therefore，

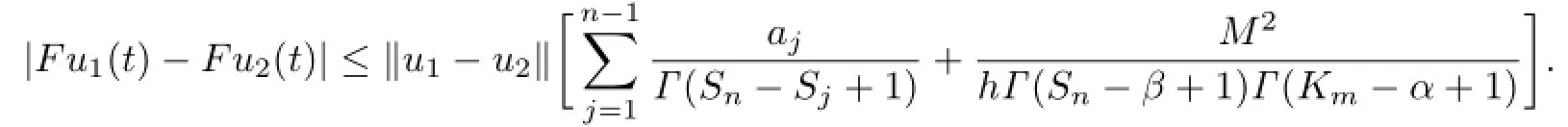
Similarly，we also have

Thus，F and G are contraction operators and so(1.1)has a unique solution.

Example 3.1Consider the system of fractional equations

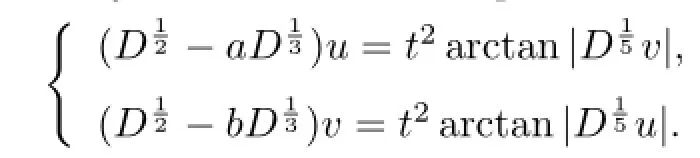
In view of Theorem 3.2 there exists a positive solution for this system.

Example 3.2The system

has a positive solution in view of Theorem 3.3.

References

[1]Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations.North-Holland Mathematics Studies.Amsterdam:Elsevier，2006.

[2]Lakshmikantham V，Leela S，Vasundhara D J.Theory of Fractional Dynamic Systems.Cambridge:Cambridge Scientific Publishers，2009.

[3]Lakshmikantham V，Vatsala A S.Basic theory of fractional differential equations.Nonlinear Anal.，2008，69(8):2677–2682.

[4]Podlubny I.Fractional Differential Equations.San Diego:Academic Press，1999.

[5]Sabatier J，Agrawal O P，Machado J.Advances in Fractional Calculus:Theoretical Developments and Applications in Physics and Engineering.Dordrecht:Springer，2007.

[6]Ntouyas S K，Obaid M.A coupled system of nonlinear fractional differential equations with integral boundary conditions.Adv.Difference Equ.，2012，2012:Article ID 130，8pp.

[7]Ahmad B，Alsaedi A.Existence and uniqueness of solutions for coupled systems of higher-order nonlinear fractional differential equations.Fixed Point Theory Appl.，2010，2010:Article ID 364560，17pp.

[8]Rehman M，Khan R.A note on boundary value problems for a coupled system of fractional differential equations.Comput.Math.Appl.，2011，61:2630–2637.

[9]Langlands T A M，Henry B I，Wearne S L.Fractional cable equation for anomalous electrodiffusion in nerve cells:infinite domain solutions.J Math.Biol.，2009，59:761–808.

[10]Yang W.Positive solutions for a coupled system of nonlinear fractional differential equations with integral boundary conditions.Comput.Math.Appl.，2012，63:288–297.

[11]Furati K M，Kirane M.Necessary conditions for the existence of global solutions to systems of fractional differential equations.Fract.Calc.Appl.Anal.，2008，11:281–298.

[12]Yang G F，Zhong M L.The uniqueness of solution for a fractional order nonlinear eigenvalue problem with p-Laplacian operator.Adv.Difference Equ.，2014，2014:Artcile ID 186，9pp.

[13]Ahmad B，Alsaedi A，Assolami A，Agarwal R P.A new class of fractional boundary value problems.Adv.Difference Equ.，2013，2013:Artcile ID 373，8pp.

[14]Tian Y S.Multiple positive solutions to m-point boundary value problem of nonlinear fractional differential equation.Differential Equations Dynam.Systems，2015，23(1):43–56.

[15]Samko S G，Kilbas A A，Marichev D I.Fractional Integrals and Derivatives:Theory and Applications.Malaysia:Gordon and Breach Science Publishers，1993.

10.13447/j.1674-5647.2016.03.07

date:Sept.22，2015.

Jilin province education department“twelfth five-year”science and technology research plan project([2015]No.58)，and the science and technology innovation fund(No.XJJLG-2014-02)of Changchun University of Science and Technology.

E-mail address:daiqun1130@163.com(Dai Q).