变论域模糊PID在无头轧制模拟实验台上的研究

王宏文，吴红星，孟立新，曹泽华

（河北工业大学 控制科学与工程学院，天津 300130）

变论域模糊PID在无头轧制模拟实验台上的研究

王宏文，吴红星，孟立新，曹泽华

（河北工业大学 控制科学与工程学院，天津 300130）

无头轧制技术作为目前轧钢业最为先进的加工方法，对未来我国轧钢业的发展有深远意义。无头轧制系统是强扰动作用下的高阶、非线性、强耦合、时变的机电控制系统，要求后一根钢坯能够快速、准确、稳定地追上前一根钢坯。针对传统PID控制器响应速度慢、稳定性差和常规模糊PID论域不变调节能力差的缺点，将变论域与常规模糊PID结合提出变论域自适应模糊PID控制器，其变论域能够提高模糊推理的精度，模糊控制能够实现PID参数的在线整定。通过仿真和实验表明，其响应速度、稳态精度和抗干扰能力优于传统PID和常规模糊PID，具有一定的推广价值。

无头轧制；多级传动；变论域模糊PID；可编程序控制器

无头轧制技术是目前国际上用于钢材生产线的一种最先进的加工方法［1］，其连续的轧制方式能够极大提高生产效率、减少能源消耗和材料的浪费。其技术核心是在复杂的工况下，后一根钢坯顶部能够快速、准确、稳定地追上前一根钢坯的尾部，并采用闪光对焊的方式焊接一起。控制器的选择对系统非常重要，传统的PID控制器虽然原理简单，但参数整定费时，对时变非线性系统调节能力不足。无头连续轧制系统是强扰动下的高阶、非线性、强耦合、时变的机电控制系统［2］。传统的PID控制器控制效果不理想，模糊控制不依赖精确的数学模型，根据工程实践和专家经验建立语言变量控制规则，对时变、非线性、强耦合难以准确建模的系统控制效果比较理想。但常规的模糊控制器的输入通常选择误差e和误差变化率ec，其控制相当于常规的PD控制器，缺少积分环节，稳态精度较低。将模糊控制与传统的PID相结合提出的模糊自适应PID，将PID的结构简单稳定可靠和模糊控制对非线性、强耦合、时变和被控对象模型不确定的系统具有很好的控制作用的特点相结合。常规的模糊PID控制器，一旦设计规则确定结构就不能更改，对于复杂的控制过程，特别是大动态范围运行时［3］，其固定论域就会使PID参数变化受模糊规则影响变大变小，从而使PID参数变化不准确。针对无头轧制钢坯追赶过程中快速、准确、稳定的特点，将变论域的思想应用到模糊自调整PID控制器中，变论域能够提高模糊推理的控制精度［4］，采用变论域模糊自调整PID控制策略并在自主研发的无头轧制实验台上对无头轧制工艺过程进行模拟，仿真和实验取得了良好的效果。

1　无头轧制模拟实验台的简介和系统模型

无头轧制多级传动模拟实验台是一个以变频器为放大器、交流电机作为执行机构、S7-400PLC作为控制器的位置随动系统［5］。PLC通过PROFIBUS/DP总线连接变频器完成过程量的给定和电机数据的上传，通过MPI总线连接上位机，采用WinCC组态软件监视和控制系统。执行机构2台异步电机和1台同步电机分别驱动下面模拟钢坯追赶过程的2个滑块和上边模拟焊接过程的焊机小车的运行，滑块和焊机小车与丝杠相连，通过编码器和高速计数器精确地采集3个滑块的位置信息上传给PLC，PLC完成对位置的精确控制。实验台电气结构图如图1所示。

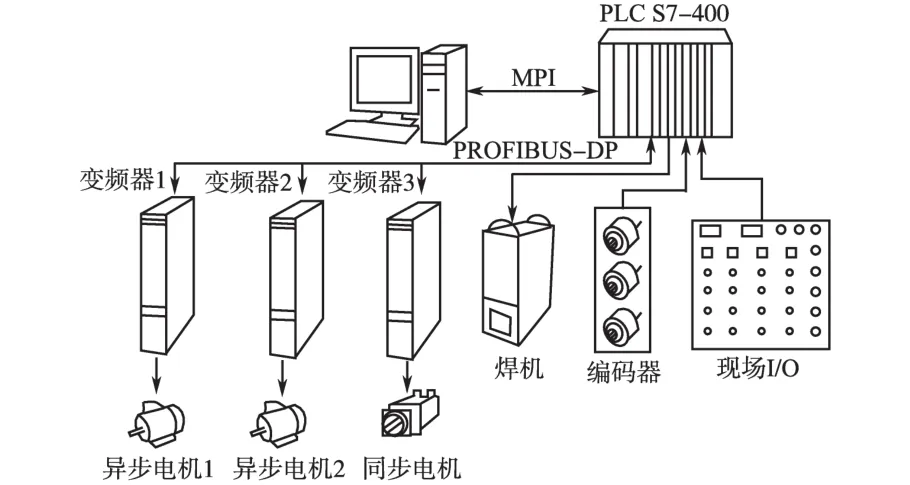
图1　无头轧制实验台电气结构Fig.1　The electrical structure of endless rolling platform

系统模型的建立在参考文献［6］中已给出严格的推导证明，最终系统的模型结构见图2。将变频器和电机等效成一个整体，其转速环和电流环的控制器ASR，ACR采用PI控制方式，由变频器内部实现，位置环控制器APR由PLC实现，本文主要是通过Matlab仿真和PLC上编程完成位置环APR进行设计。

图2　实验台位置随动系统结构Fig.2　The structure of position servo system

2　变论域模糊PID的设计

2.1模糊自调整PID控制器

模糊自适应PID控制器的系统结构主要是由模糊控制系统和参数可调的PID控制器组成［7］。控制器在传统PID控制器的基础上，加入模糊控制算法将位置误差e和误差的变化率ec作为输入通过不断检测系统e和ec的变化来实时调整PID控制器的3个参数。将模糊控制较好的鲁棒性、稳定性、对非线性时变系统良好的控制性能和PID控制的实时性、快速性相结合，很大程度改善控制器的性能。模糊PID结构见图3。

控制器采用2输入3输出的结构形式，输入选取位置误差e和误差的变化率ec，PID 3个参数的变化量ΔKP，ΔKI，ΔKD作为输出量。e和ec的语言变量为E，EC，e和ec通过乘以量化因子Ke，Kec，将其转化到论域E，EC上，模糊控制器输入变量e 和ec和输出变量ΔKP，ΔKI，ΔKD的论域为｛-E，E｝，模糊语言值为｛PB，PM，PS，ZO，NS，NM，NB｝，隶属度函数选取三角形隶属度函数的形式。

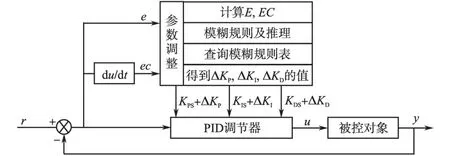
图3　常规Fuzzy PID控制器结构Fig.3　The structure of conventional Fuzzy PID controller

根据工程经验和专家知识调整PID参数，采用常规的模糊条件ifA and B then C进行模糊合成推理，建立ΔKP，ΔKI，ΔKD的模糊规则表，如表1所示。

表1　ΔKP，ΔKI，ΔKD模糊规则表Tab.1　Fuzzy reasoning table of ΔKP，ΔKI，ΔKD

模糊推理采用Mamdani法则，解模糊采用重心法见下式：

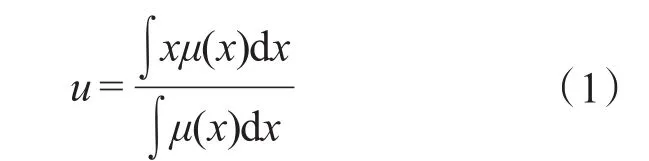
将模糊量转化为精确的控制量。

通过解模糊求得ΔKP，ΔKI，ΔKD在其模糊论域的精确值，乘以比例因子K1，K2，K3得到最终的ΔKP，ΔKI，ΔKD的值，通过下式：

最终得到控制器当前KP，KI，KD的值。

量化因子Ke，Kec和比例因子K1，K2，K3为模糊控制器的参数，对模糊控制器有重大影响。根据系统实际运行的动态范围，e=［emin，emax］，ec= ［ecmin，ecmax］，Δkm=［Δkmmin，Δkm man］（m为p，i，d），输入变量e，ec和输出变量ΔKP，ΔKI，ΔKD的模糊论域为｛-E，E｝，定义量化因子和比例因子的修正关系为

其中，m=1，2，3。

2.2变论域模糊控制原理

常规模糊PID一旦设计完成其结构就固定，不能更改，自适应能力有限。当输入e，ec的论域选择过大输入量较小时，只会用到其少量的模糊集合和隶属函数；反之，输入论域过小，对于较大的输入，模糊控制的调整量不足，从而控制效果变差。输出论域过大，会使ΔKP，ΔKI，ΔKD过大，从而使系统出现震荡、抗干扰能力变差等；论域过小会使PID参数调整不足，控制效果变差。

基于以上常规模糊PID的不足，将变论域的思想融入模糊PID中。李洪兴教授1999年在文献［4］中正式提出变论域的思想。变论域是指输入输出论域随着误差和控制要求的变化按照一定准则，适当地进行变化［8］。其思想是在规则形式不变的前提下，论域随着误差变小而收缩（亦可随着误差增大而扩展）［9］。论域伸缩变化如图4所示。

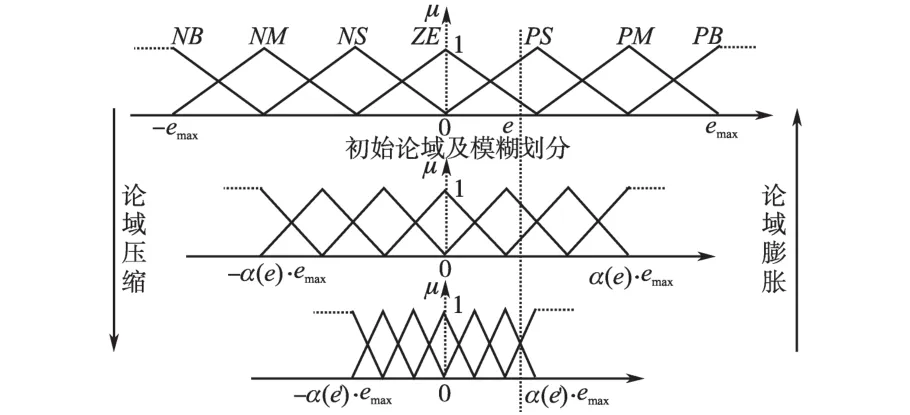
图4　论域的伸缩变化示意图Fig.4　The change diagram of universe constricting and expending

设输入x的基本论域为［-E，E］，输出u的基本论域为［-U，U］，则变论域上的输入论域x通过伸缩因子α变为 ［-αE，αE］，输出论域u通过伸缩因子β变为［-βU，βU］［10］。目前，伸缩因子的形式没有统一的标准，常用于构造伸缩因子的方法主要有2种：一种是采用模糊推理的方法，另一种是基于e，ec的函数型设计方式；本文伸缩因子采用基于函数型的设计。输入量e，ec的伸缩因子为

式中：τ为常数，0＜τ＜1。

根据当前e，ec的变化所反映的系统当前状态，确定输出论域的伸缩因子为

式中：K为比例常数；设计参数β（0）通常取0，然后根据实际调整。

大量对于量化因子和比例因子的研究表明，不改变模糊控制器的结构，调整模糊控制器的量化因子和比例因子，实际上是把模糊控制器中论域压缩或扩张，与变论域思想本质上相同［11］。量化因子增大，相当于收缩输入论域，反之相当于扩张输入论域；比例因子放大，相当于扩张输出论域，反之相当于收缩输出论域。本文基于量化因子和比例因子的特点，根据e，ec调整量化因子和比例因子，达到论域收缩的效果。变论域模糊自调整PID的结构如图5所示。

图5　变论域Fuzzy PID结构图Fig.5　The structure of variable universe fuzzy PID

3　变论域模糊PID的PLC程序设计

变论域模糊PID控制器采用PLC的软件实现，将其看作是总体程序的一个子程序，软件的编写在SIEMATIC STEP7中完成。将程序分为变论域和常规的模糊PID两部分。变论域部分主要是根据实际的输入计算出相应的量化因子Ke，Kec和比例因子K1，K2，K3，完成实际论域的伸缩和扩张。常规的模糊PID设计首先通过Matlab编程离线计算出模糊规则查询表，将模糊规则查询表存储在PLC的数据块DB中，编写查表子程序，选用基址加偏移地址的方法［12］，该方法设计简单，运算速度快。通过高速计数器采集编码器的脉冲信号得到滑块的实际位置，通过计算得到位置差及变化率e和ec，分别乘以变论域处理后的量化因子Ke，Kec得到其在变论域上的E和EC。查表子程序得到ΔKP，ΔKI，ΔKD的论域值，乘以变论域处理后的比例因子K1，K2，K3得到当前的ΔKP，ΔKI，ΔKD值，通过式（2）得到当前的KP，KI，KD的值，再将得到的KP，KI，KD的值写入PLC的FB41功能块中。变论域模糊控制器程序结构图如图6所示。

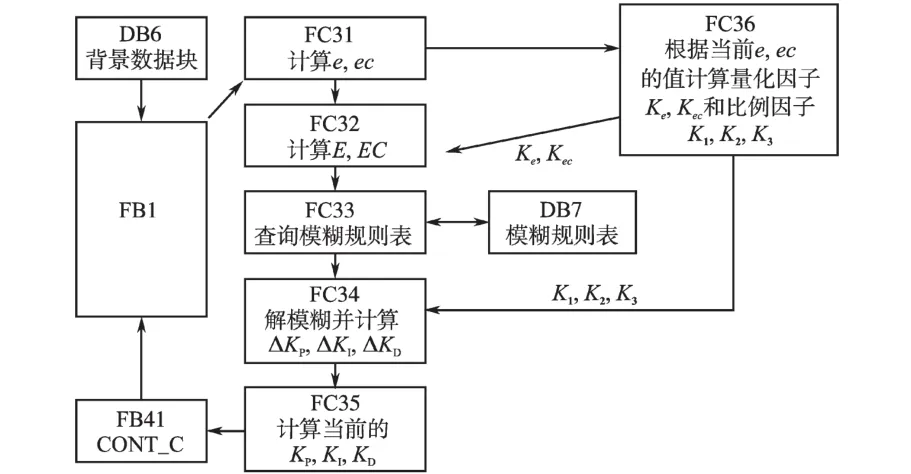
图6　变论域Fuzzy PID PLC程序结构图Fig.6　The PLC program structure of variable universe fuzzy PID

4　系统仿真及实验结果

根据参考文献［5］可知，系统模型中Kv=22，T=0.003 41 s，J=9.398 kg·m2，ASR控制器P=7，I= 0，ACR的控制器参数为P=1，I=2。仿真1给定1 000 mm的位置阶跃信号，APR控制器分别采用PID、常规模糊PID和变论域模糊PID 3种控制器，系统仿真模型见图7。

图7　系统仿真模型Fig.7　The simulation model of the system

APR控制器参数初调为P=7，I=0，D=0.5，3种控制器初始PID参数都相同，根据公式模糊控制器的量化因子Ke=0.6，Kec=0.36，考虑系统的稳定性和快速性，量化因子K1=3，K2=20，K3=1/4。变论域模糊PID控制器和模糊PID模糊参数完全相同。电机转速限幅为3 000 r/min。位置曲线和速度曲线如图8、图9所示。

图8　1 000 mm位置阶跃曲线Fig.8　1000mmpositionstepcurves

图9　电机速度曲线Fig.9　Motor velocity curves

比较3种控制方式的阶跃曲线，可以看出曲线初始时由于电机转速限幅的原因，3种控制器都被限制在限幅值上，初始时曲线上升速度相同，随着误差的减小，电机速度逐渐小于最大限幅值，其控制器的效果有明显差别，变论域模糊PID曲线上升速度快，传统PID、常规模糊PID、变论域模糊PID达到稳态时间分别是13.5 s，8.3 s，5.2 s。当在20 s受到扰动后，变论域模糊PID受扰动影响较小并且能够快速地恢复稳定，其抗干扰能力明显优于传统地PID和常规模糊PID控制器。

仿真2模拟钢坯追击过程，给定初始位置误差700 mm，同时给定曲线以15 mm/s的速度运动，3种控制器初始PID参数为P=7，I=0.06，D= 0.6，模糊控制器的量化因子和比例因子为Ke= 0.857，Kec=0.6，K1=3，K2=20，K3=1/4最终得到3种控制方式的曲线如图10所示。

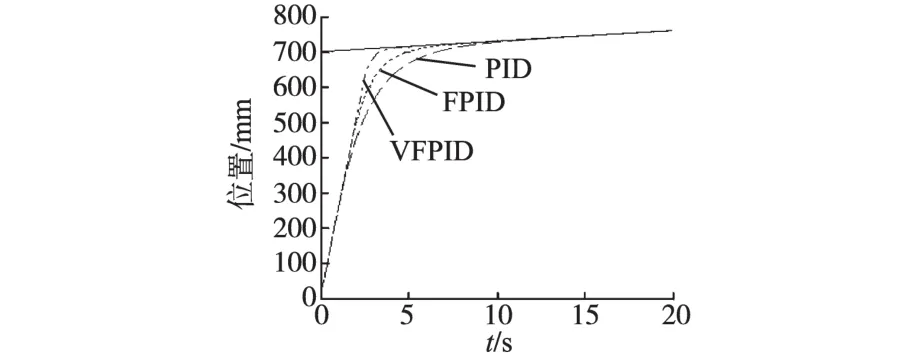
图10　初始位置差700 mm斜坡仿真曲线Fig.10　The 700 mm difference between the initial position slope simulation curves

3种控制器仿真曲线追踪上的时间分别为10.6 s，8.3 s，4.9 s，由此可见变论域模糊PID能够大幅度缩短追击时间。

在无头轧制多级传动模拟实验台上实验，通过WinCC读出2块钢坯的位置差曲线，实验主要比较常规模糊PID和变论域模糊PID两种控制方式的曲线，实验结果见图11a、图11b，实验结果表明，与常规模糊PID控制器相比，变论域模糊PID的追击时间较其缩短近14 s，而且调节时间短。

图11　实验结果Fig.11　The experimental results

5　结论

无头轧制工艺过程要求钢坯位置的精确控制和快速追赶焊接，对动、静态性能指标要求都很高，所以控制器的选择非常重要。本文根据无头轧制工艺过程中钢坯追赶时快速、稳定、准确的特点，对PID、模糊PID、变论域模糊PID 3种控制方法进行了比较。

仿真结果表明变论域模糊PID响应速度和抗扰能力方面都优于传统的PID控制器和常规模糊PID控制器，变论域模糊PID控制器其论域能够随误差的变化而进行伸缩和扩张，模糊规则能够完全地应用整个控制过程，其性能更优于常规模糊PID控制器，具有一定的推广意义。

［1］ 刘通学.无头轧制多级传动系统控制策略的研究与开发［D］.天津：河北工业大学，2007.

［2］ 王宏文，刘通学，刘丽.无头轧制多级传动模拟实验平台的研究与开发［J］.制造业自动化，2008，1（30）：23-25.

［3］ 崔家瑞，李擎，祝乔.飞航导弹变论域自适应模糊PID控制方法［J］.控制工程，2014，21（6）：848-852.

［4］ 李洪兴.变论域自适应模糊控制器［J］.中国科学（E辑），1999，29（1）：32-42.

［5］ 常鸿飞.无头轧制多级传动模拟实验台的研究与开发［D］.天津：河北工业大学，2007.

［6］ 王宏文，柳溪，卢鹏飞.无头轧制多级传动系统建模与仿真［J］.制造业自动化，2009，31（6）：89-92.

［7］ 李国友，高宁宁，卢杰键.蒸汽过热炉温度模糊自适应PID控制［J］.计算机与应用化学，2014，12（31）：1539-1542.

［8］ 尹玲玲.船舶柴油机变论域模糊PID转速控制研究［D］.重庆：重庆大学，2010.

［9］ 潘琢金，温文博，杨华.变论域模糊PID在空调车温度控制中的应用［J］.计算机仿真，2011，28（10）：43-46.

［10］韦延方，董爱华，吕国栋，等.造纸机速度链的变论域模糊PID控制［J］.电气传动，2009，39（8）：52-55.

［11］潘永平，王钦若.变论域自适应模糊PID控制器设计［J］.智能控制技术，2007，29（3）：9-11.

［12］吴明永.工业锅炉控制策略研究与控制系统设计［D］.兰州：兰州理工大学，2009.

Study on the Platform of the Endless Rolling System of Variable Universe Fuzzy PID

WANG Hongwen，WU Hongxing，MENG Lixin，CAO Zehua
（School of Control Science and Engineering，Hebei University of Technology，Tianjin 300130，China）

As the most advanced processing method in current steel rolling industry，endless rolling technology has far-reaching significance for the development of steel rolling industry.Endless rolling system is a higher order，non-linear，strong coupling，time-varying electromechanical control system under strong disturbance.It needs the second steel billet catches up with the first one quickly，accurately and stablely.The traditional PID controller has the slow response and poor stability，while the constant universe of conventional fuzzy PID leads to its poor control capability.Combined with variable universe and conventional fuzzy PID to propose variable universe adaptive fuzzy PID controller，which variable universe could improve the accuracy of fuzzy control and fuzzy control could achieve PID parameters tuning online.The simulation and experimental results show that its response speed stability accuracy，disturbance rejection ability are better than traditional PID and conventional fuzzy PID，it is valuable to use and popularize.

endless rolling；multi-drive；variable universe fuzzy PID；programmable logic controller（PLC）

TP273

A

2015-09-27

修改稿日期：2016-04-18

王宏文（1957-），男，工学硕士，教授，Email：wanghongwen@hebut.edu.cn