基于高频注入的永磁同步电机无位置传感器鲁棒性分析

何忠祥，朱磊，李明勇

（武汉船用电力推进装置研究所，湖北 武汉 430064）

基于高频注入的永磁同步电机无位置传感器鲁棒性分析

何忠祥，朱磊，李明勇

（武汉船用电力推进装置研究所，湖北 武汉 430064）

针对表贴式永磁同步电机给出了一种基于脉振高频电压信号注入的转子位置辨识方法。首先对该辨识策略的基本原理进行了介绍，给出可以应用在低速和静止下的辨识模型；其次，推导出该模型的位置估计误差，进而对该模型的稳定性和鲁棒性进行了分析。分析发现，无论是处于低速还是静止状态，该模型表现很好的稳定性和鲁棒性，并且不依赖电机参数，仿真分析验证了理论分析的正确性和所提策略的有效性。

表贴式永磁同步电机；无位置传感器；高频脉振电压注入；鲁棒性

永磁同步电机以其尺寸小、功率密度高、动态性能好等优点，在风力发电、船舶电力推进等领域越来越受到人们的重视。永磁同步电机多采用矢量控制或直接转矩控制的方式，无论哪种控制方案都需要转子位置信息进行运算。位置信息通常由旋转变压器、编码器等传感器提供，这些机械装置无疑会增加系统的成本、重量和尺寸，降低系统的可靠性。鉴于此，永磁同步电机无位置传感器控制受到广泛的关注。

基于电机基频模型，很多学者建立了转子位置与反电动势、磁链等状态量之间的关系，提出了一系列的辨识策略［1］；但当电机处于低速甚至静止状态时，这些策略由于所需状态量过小或者根本无法检测无法使用。低速下位置的辨识大多利用电机的凸极效应，这里的凸极效应既可以由电机固有的结构引起，也可以由内部磁路饱和引起。文献［2］通过分析电感随转子位置变化的规律，提出注入幅值相等、相位变化的电压脉冲信号，根据响应电流的大小判断转子初始位置。文献［3］详细讨论了高频旋转电压信号注入法和高频脉振电压信号注入法在转子位置估计中的应用，指出基于高频脉振注入的方法比较适合表贴式这类非凸极性永磁同步电机。文献［4-6］的分析指出，电机的结构不同时，当向直轴注入电压信号时，dq轴电感的变化既可由主磁路的饱和引起，也可由漏磁路的变化引起，在对电感进行有限元分析的基础上，它们都结合高频信号注入法实现了转子位置的估计。文献［7］为了简化计算，通过向d轴注入脉冲信号也实现了初始位置的估计，但其推导过程做了大量的假设，且位置辨识误差随转速呈线性变化。根据信号注入的原理，一系列位置辨识策略被应用于永磁同步电机无传感器控制应用中，但位置误差和辨识策略稳定域却很少被分析研究。

本文在分析表贴式永磁同步电机（SPMSM）因内部磁路饱和引起凸极效应的基础上，根据永磁同步电机在高频激励下的模型，得出可以应用在低速和静止工况下的转子位置的辨识算法。另外，在对位置估计误差进行分析的基础之上，对该模型的稳定域和鲁棒性进行了分析。该方法不需要添加额外的硬件，鲁棒性强，通过仿真分析验证了本文所提出方法的有效性。

1　脉振高频电压信号注入

1.1永磁同步电机高频激励模型

为了提高铁磁材料的利用效率，SPMSM直轴磁路空载时的工作点通常设计在Ψ—i特性曲线的拐点处。当向电机直轴注入正向电流id+时，直轴电流产生的磁场和永磁体产生的磁场方向相同，这会加深直轴磁路的饱和程度［2］，使得直轴电感Ld减小；由于交轴磁路工作点位于Ψ—i特性曲线的原点处，不易饱和，Lq恒定，因而有Ld+＜Lq。

不计涡流损耗和磁滞效应影响，并假设磁场正弦分布，可得SPMSM高频激励下的模型［5］为

式中：udh，uqh，idh，iqh分别为转子真实d-q坐标系下定子高频电压和电流分量；Rdh，Ldh，Lqh分别为dq轴的电阻和电感；p为微分算子。

定义θ为电机转子d轴真实位置，θ̂为电机转子d轴辨识的位置，Δθ=θ-θ̂为电机转子真实位置和辨识位置的角度差，如图1所示。

图1　真实d-q和辨识d̂-q̂坐标系Fig.1　The estimated referenced̂-q̂frame and practicald-qreference frame

从图1可以得到真实和辨识之间的坐标变换矩阵如下：

由于Rd，q≪ωhLd，q，忽略定子电阻的影响，根据坐标变换，可得

考虑到电流调节器带宽、电压传感器成本和输出转矩波动等问题，通常选择向d轴注入高频脉振电压信号，通过测量电流信号得到位置信息。

其中L=（Lqh+Ldh）/2ΔL=（Ldh-Lqh）/2

从式（4）可知，电流idh和îqh都可以看成随位置变化的正弦量。辨识位置差Δθ=0时，≠0，=0，因而，可以将作为自变量得到。

1.2基于高频脉振电压信号注入位置辨识

当转子位置辨识值和真实值之间误差很小时，sin（2Δθ）≈2Δθ，将 f（Δθ）信号经过比例积分调节器就可以获得转子速度的辨识值，辨识速度再经过积分环节就得到转子的位置信息。

式中：kp，ki为PI调节器的参数。

根据式（6）、式（7），可得转子位置辨识的反馈系统如图2所示。

图2　位置辨识等效反馈系统Fig.2　The equivalent feedback system of position estimation

图2中：

由于SVPWM和采样等产生的高频电流成分经过前面介绍的低通滤波器环节可以有效地滤除，iqh可以通过将采样电流直接通过高通滤波器获得。至此，可以得到基于高频脉振电压注入的转子位置辨识控制结构图如图3所示，当进行初始位置估计时，也可以将f（Δθ）通过PI的结果直接作为转子的初始位置，用以减小辨识系统的阶数。

图3　位置估计原理框图Fig.3　Principle diagram of rotor position estimation

2　转子位置辨识误差分析

上面公式的推导忽略电阻、基频、转子磁链等因素的影响，下面根据电机基本模型，分析因为高频模型的简化给转子位置辨识带来的误差。

从式（3）、式（8）可得：

其中

再结合式（2），可得：

同样经调制和低通滤波后，可得：

由式（5）、式（9）可知，位置辨识的误差主要由A引起，电阻、dq轴高频电感和基波频率都会影响辨识位置的精确度。因而，有必要分析上述模型在低速和零速辨识时的稳定性和鲁棒性。

电机低速运行时，电机位置、转速辨识值通过电机的机械结构构成辨识系统的闭环。选择合适的辨识参数，位置辨识值和真实值的差异通过电机输出反馈进行动态调节，误差很小。

转子处于静止状态时，有ω=dθ/dt=0。

这种流变并不有损元曲的典范地位，反而意味着明代文人越来越注重对元曲在多个角度的分析与学习，并最终借鉴到明代曲的创作与欣赏过程中来。换而言之，这一流变过程从一个更合理的角度，更加固化了元曲在文坛的标志性成就和经典化地位。

令σ=∫f（Δθ）dt，则有

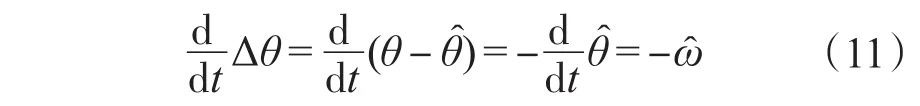
将辨识位置差和σ作为状态变量，可得：

若采用此控制策略位置辨识值能够收敛至真实位置，即 f（Δθ）积分值σ恒定，Δθ趋于0，则上面状态方程的特征根必须满足小于0的条件。

从式（13）可得：

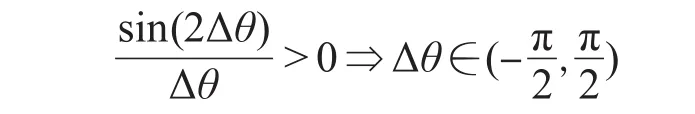
由上式可知，初始位置辨识时该系统的稳定域为Δθ∈（-π/2，π/2），这也从另一方面解释了进行转子初始位置辨识时进行直轴正方向判断的必要性，直轴正方向的判断可以通过检测通入正反方向直流电压id电流的峰值或衰减时间判断。从中还可以看出该稳定性判定条件和电机参数、电机运行状态没有关系，这说明该辨识策略在进行初始位置判断时也具有很好的鲁棒性。

3　仿真分析

高频信号幅值和频率的选择对位置辨识的影响很大。选择注入电压幅值时：若幅值过高，电机会产生较大的转矩波动，甚至会发生转动；若幅值过低，辨识收敛较慢。选择注入电压频率时：若频率过高，会造成采样信号的混叠；若频率过低，则高频激励下的电机模型就不再成立。

下面进行转子初始位置的仿真分析。给定转子初始位置为5 π/6，可得图4。从中可以发现在0.3 s之后位置辨识输出值不再变化，这是由于此时Δθ=π已经超出辨识稳定域的原因，在0.7 s再结合直轴的判断就可以得到真实的转子位置。

图4　转子初始位置为5π/6时的辨识波形图Fig.4　The identification of motor initial position asθ=5π/6

接着分析低速运行的位置辨识。给定电角频率为52.36 rad/s（对应电机100 r/min），可得辨识波形图如图5、图6所示。仿真中采用变PI的控制用以兼顾动态跟随和稳态精度的性能要求。图5a为速度辨识误差变化波形图，图5b为辨识转速和真实转速的波形图，转速误差在±3 rad/s以内，误差平均值为0，满足矢量控制的要求；图6a为位置辨识的误差，图6b为辨识和真实位置的波形图，从中可以看出，辨识位置差在-0.01 rad附近波动。

图7为当电角速度给定在15 s由52.36 rad/s变为104.72 rad/s（对应电机200 r/min）时，转速和位置辨识误差的波形图。从中可知，给定突然变化时，位置和速度辨识误差都会短暂增加，但随着系统的稳定，辨识误差会逐渐减小，这说明所用的控制策略能够有效抑制动态扰动。

图5　ωe_ref=52.36 rad/s，电机速度辨识波形图Fig.5　The speed estimation asωe_ref=52.36 rad/s

图6　ωe_ref=52.36 rad/s，电机位置辨识波形图Fig.6　The position estimation asωe_ref=52.36 rad/s

图7　给定改变时，辨识误差波形图Fig.7　The estimated err when the given is changed

4　结论

本文针对表贴式永磁同步电机提出一种基于高频脉振信号注入的转子位置辨识策略。在

旋转坐标系下建立了表贴式永磁同步电机的高频模型，基于此模型提出了静止和低速下的位置辨识算法，形成了无位置传感器的控制策略，还对所提方法的稳定性进行了分析，确定了其稳定域。本方法不依靠电机的准确参数，不需要额外的传感器等硬件，可以很好地移植到内嵌式等结构性凸极的永磁同步电机。仿真结果表明该方法具有良好的辩识精度和稳定性，能够满足永磁电机静止和低频时的控制需求。

［1］Paul P Acarnley，John F Watlon.Review of Position Sensor⁃less Operation of Brushless Permanent Mangnet Machines［J］. IEEE Trans.on Industry Electronics，2006，53（2）：352-362.

［2］Shin Nakashima，Yuya Inagaki，Ichiro Miki.Sensorless Initial Rotor Position Estimation of Surface Permanent Magnet Syn⁃chronous Motor［J］.IEEE Trans.on Industry Application，2000，36（6）：1598-1603.

［3］ 秦峰，贺益康，刘毅，等.两种高频信号注入法的无传感器运行研究［J］.中国电机工程学报，2005，25（5）：116-121.

［4］ Jeong Y S，Lorenz R D，Jahns T M，et al.Initial Rotor Position Estimation of an Interior Permanent Magnet Synchronous Ma⁃chine Using Carrier Frequency Injection Methods［J］.IEEE Trans.on Industry Application，2005，41（1）：38-45.

［5］Jung Ik Ha，Seung Ki Sul，Kozo Ide，et al.Physical Under⁃standing of High Frequency Injection Method to Sensorless Drives of an Induction Machine［C］//IEEE Industry Applica⁃tions Conference，2000，3：1802-1808.

［6］Ji Hoon Jang，Seung Ki Sul，Jung Ik Ha，et al.Sensorless Drive of Surface Mounted Permanent-magnet Motor by High Frequen⁃cy Signal Injection Based on Magnetic Saliency［J］.IEEE Trans. on.IndustryApplications，2003，39（4）：1031-1039.

［7］Sami Zaim，Babak Nahid Mobarakeh.Robust Position Sensor⁃less Control of Nonsalient PMSM at Standstill and Low Speeds ［J］.IEEE Journal of Emerging and Selected Topic in Power Electronics，2014，2（3）：640-649.

Robust Sensorless Control of the SPMSM Based on High Frequency Injection

HE Zhongxiang，ZHU Lei，LI Mingyong
（Wuhan Institute of Marine Electric Propulsion，CSIC，Wuhan 430064，Hubei，China）

A sensorless control algorithm based on high frequency pulsating voltage injection used in a surface permanent magnet synchronous motor（SPMSM）was presented.The basic theory of the estimation strategy was introduced，and the estimation model used in low speed range including standstill was provided concretely.The analysis of the estimated error and the mathematical proof of convergence was presented.The analysis showed that the convergence of this strategy does not depend on the machine parameters at low speed or zero，which demonstrated the stabilization and robustness of the presented sensorless algorithm.The simulation results show the validity of the theoretical analysis and the feasibility of the estimation strategy.

surface permanent magnet synchronous motor；sensorless；high frequency pulsating voltage injection；robustness

TM341

A

2015-09-20

修改稿日期：2016-01-21

何忠祥（1991-），男，硕士研究生，Email：237632488@qq.com