具时滞全局耦合相振子模型的稳定性

苏日娜

（内蒙古民族大学数学学院，内蒙古通辽028043）

具时滞全局耦合相振子模型的稳定性

苏日娜

（内蒙古民族大学数学学院，内蒙古通辽028043）

在耦合强度和延迟反馈强度存在的条件下，研究具时滞全局耦合相振子延迟反馈模型，通过对其特征值分布的讨论，对模型的稳定性进行分析，讨论周期解的存在性及Hopf分支发生的条件.

时滞；耦合系统；周期解；Hopf分支

全局耦合相振子模型是一类能够模拟独立神经元同步现象的动力学系统［1-2］，它描述了全局耦合相振子的集体同步现象可以通过延迟反馈被抑制或促进［3-5］.考虑到多点延迟反馈的刺激与时滞和极性同样重要，因此为了解决一些重要的问题，对具有延迟反馈的全局耦合相振子系统的研究非常有意义［6-11］.本论文对一个全局耦合相振子的重要模型进行了讨论，这个模型描述了多点延迟反馈对由疾病引起的神经元的同步和有缺陷的中枢神经反射器的神经病患的刺激的影响.

1 稳定性

讨论时滞全局耦合相振子延迟反馈系统［12］：

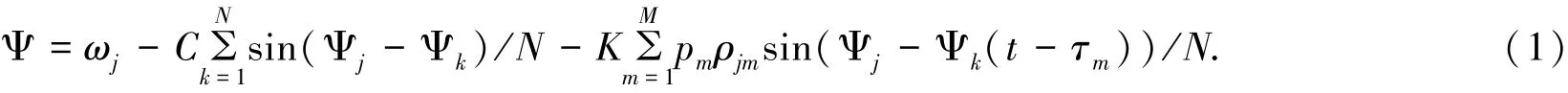
其中：C是耦合强度，N是振子的总数，K是延迟反馈的强度.有M个不同的极性pm=±1，这里平均场通过不同的电极进行传递，ρjm是额外的系数，ωj代表第j个振子，τm（m=1，2，…）是时滞.在文献［12］中，学者主要在C=0和K=0的情况下对系统的动力学性质进行了分析，并且描述了关于锁相周期解的物理现象.

在本文中，主要研究在C≠0且K≠0的情况下，N=2，M=2系统周期解的存在性.此时系统表示两个振子ω1，ω2.ρ11表示电极1对振子1的作用，ρ12表示电极1对振子2的作用，ρ21表示电极2对振子1的作用，ρ22表示电极2对振子2的作用，即自身对自身的作用相等ρ11=ρ22，外界对自身的作用ρ12=ρ21，C/2=a，（a＞0），K（ρ11-ρ12）/2=h，K（ρ21-ρ22）/2=-h，（h＞0）.利用泰勒公式（1）可化为：

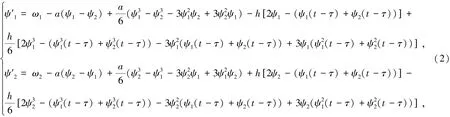
本文的目的是同时考虑物理和数学的因素来确定系统（2）的渐进行为.由于多重延迟反馈是控制时空同步模式的有效方法，不同的空间刺激与时滞和极性是一样重要.因此分析系统（2）的动力学性质越来越有意义.通过讨论系统（2）特征方程的特征根的分布情况去分析周期解的存在性和时滞穿过一序列临界值发生Hopf分支的条件［13-14］.也就是说，在直接或间接耦合振子之间实现空间的同步过程，时滞扮演了非常重要的角色.如果系统趋于稳定，那么两个振子可以达到非常完美的同步，如果系统不稳定，则振子间无法达到同步.

假设令（u1u2）为系统（2）的稳定点，且（u1u2）满足下式：

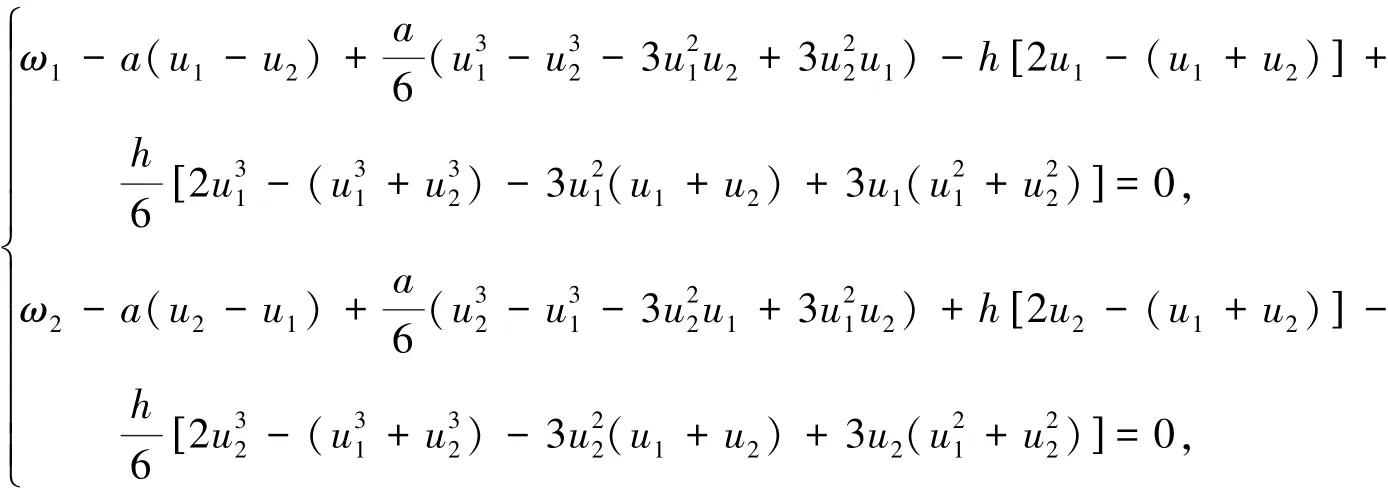
求出：

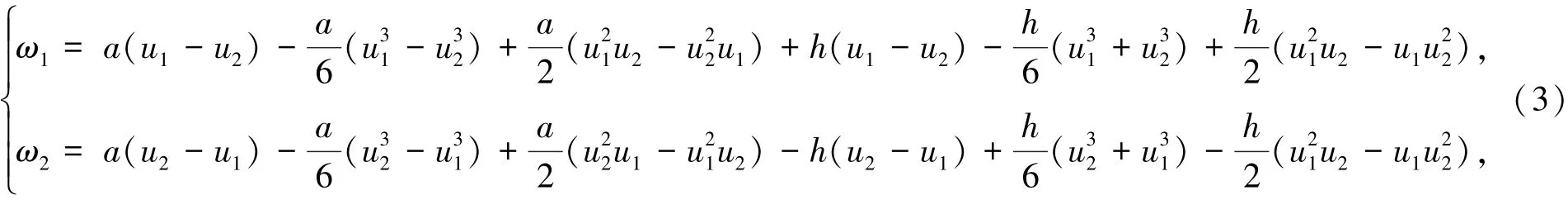
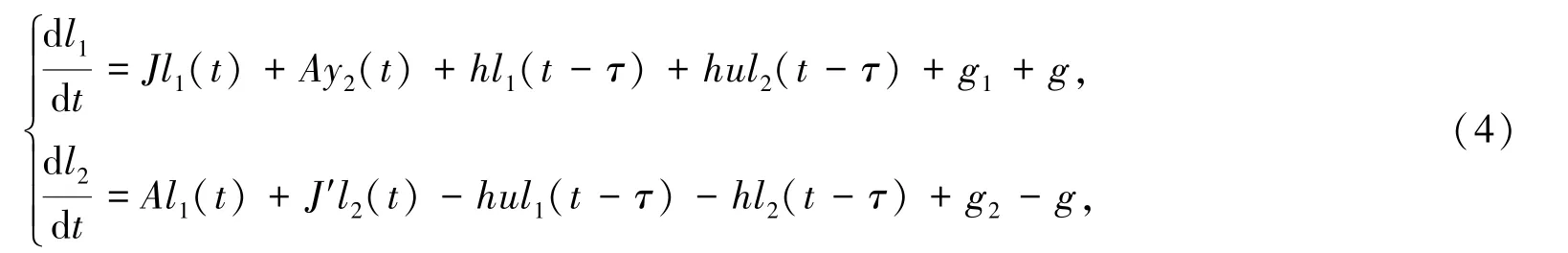
其中：

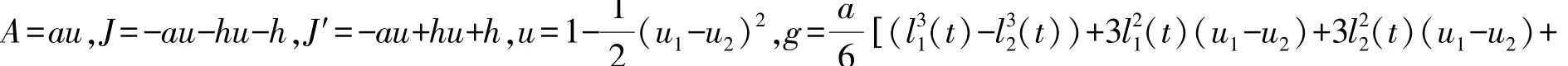
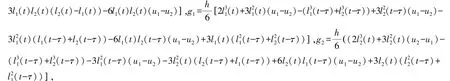
模型（4）在（0，0）处的线性部分为：

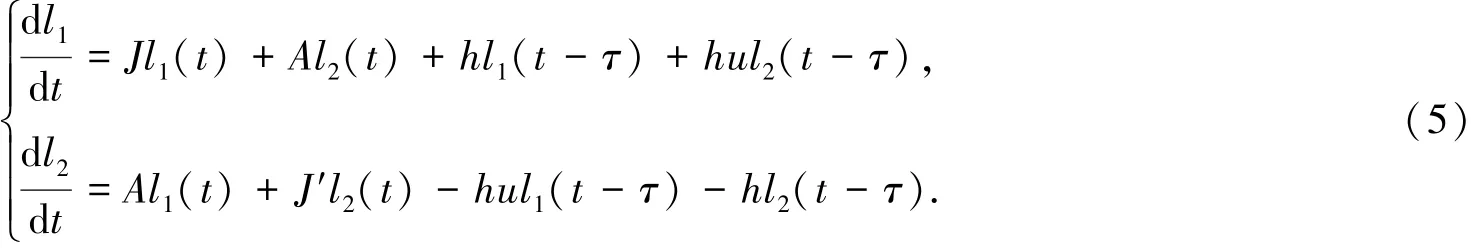
相应的特征方程为：

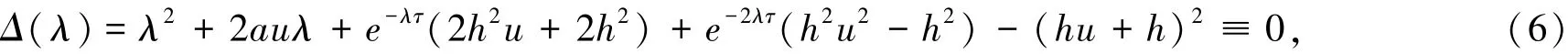
对于τ=0变为：

定理1

（i）如果u＞0，当λ∈（-2au0）时，模型（7）的所有的根都具有负实部，此时系统是渐近稳定的；

（ii）如果u＜0，模型（6）至少含有一个具有正实部的根，此时系统是不稳定的.

现在假设τ＞0，令iβ（β＞0）是模型（6）的纯虚根.将它代入到模型（6）中并分离实部与虚部后得到：

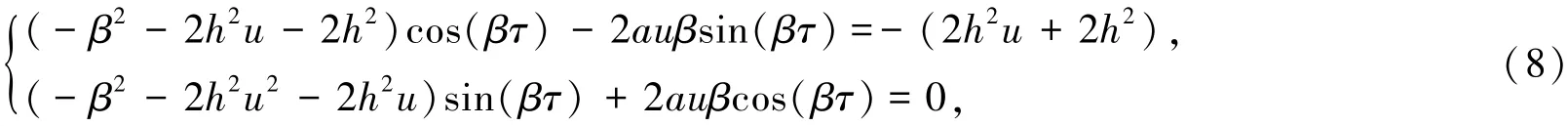
继续化简后得到：

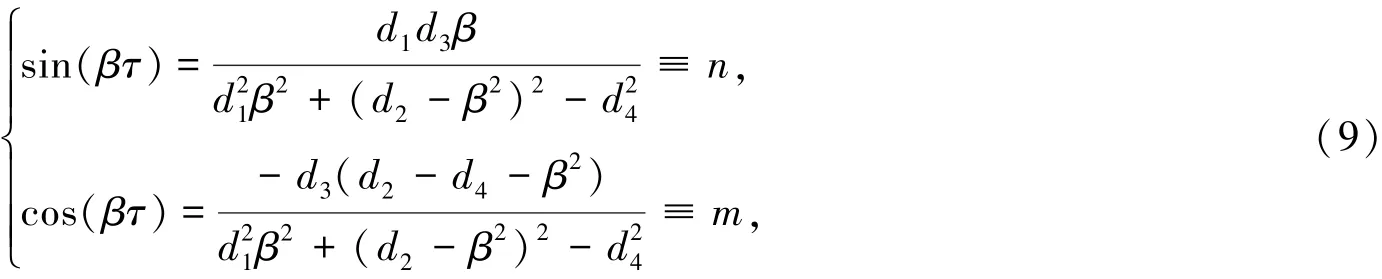
其中：d1=2au，d2=-h2（u+1）2，d3=2h2（u+1），d4=h2（u2-1）.

平方后得到：

由于计算极其复杂，假设当且仅当f3=0时的情况下进行计算，求出：

由式（9）可以得到：

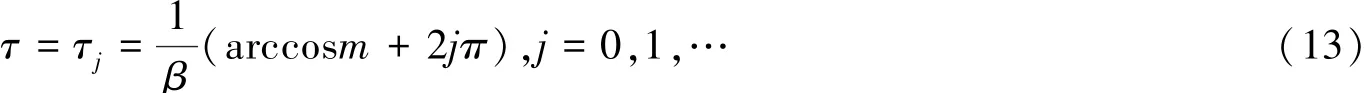
定义λ（τ）=α（τ）+iβ（τ）是模型（6）的根，且有α（τ）=0和iβ（τ）=β0，则得到如下结论.

定理2 当-1＜u＜0时，系统在τ=τj（j=0，1，…）处发生Hopf分支，存在周期解.

证明 对模型（6）中的τ进行求导，得到：

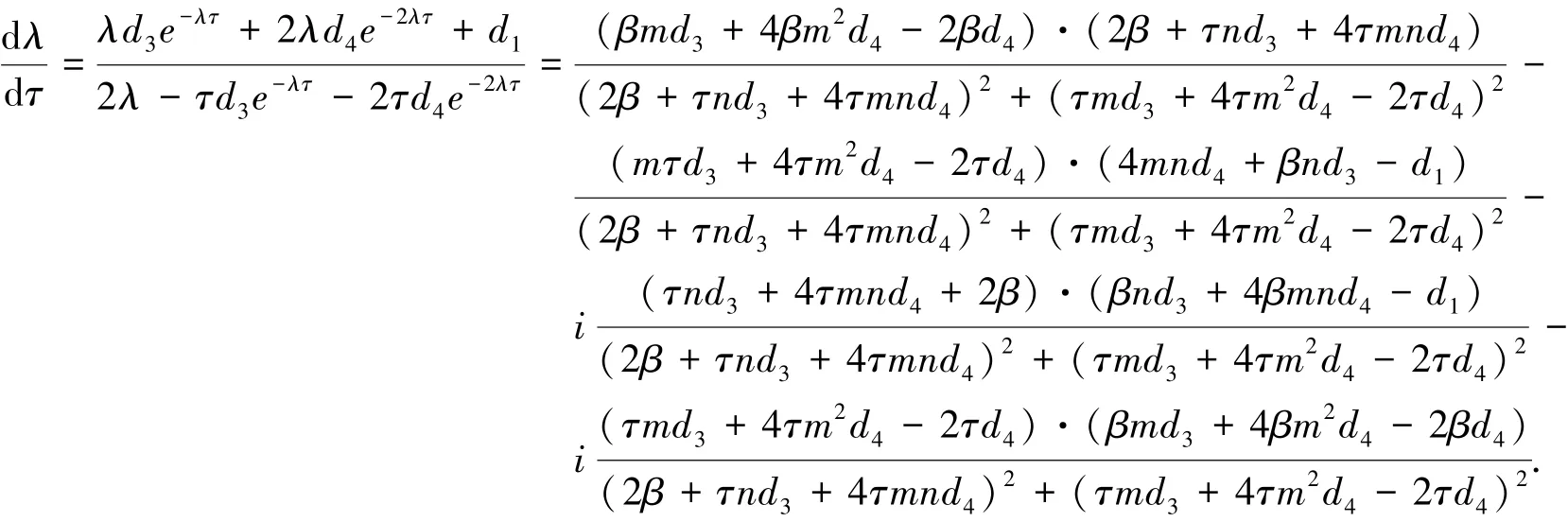
2 结论

本文主要研究了具有时滞的全局耦合相振子模型的动力学性质.在系统中，通过假设振子对自身的影响以及振子对振子之间的影响二者反作用，重组系统得到新的微分模型.求出当不存在时滞（τ=0）时系统的稳定区间以及存在时滞（τ≠0）的情况下，通过分析系统相应的特征方程根的分布，证明了系统周期解的存在性.

［1］ BROWN E，HOLMES P，MOEHLIS J.G1oba11y coup1ed osci11ator networks［J］.New York：Springer，2003：183-215.

［2］ IZHIKEVICH E M.Dynamica1 Systems in Neuroscience：The Geometry of Excitabi1ity and Bursting［M］.Cambridge：MIT Press，MA，2007.

［3］ NIEBURE E，SCHUSTER H，KAMMEN D.Co11ective frequencies and meta stabi1ity in networks of 1imit-cyc1e osci11ators with time de1ay［J］.Phys Rev Lett，1991，67：2753.

［4］ ROSENBLUM M，PIKOVSKY A.Contro11ing synchronization in an ensemb1e of g1oba11y coup1ed osci11ators［J］.Phys Rev Lett 2004，92：114102.

［5］ YEUNG M，STROGATZ S.Time de1ay in the Kuramoto mode1 of coup1ed osci11ators［J］.Phys Rev Lett，1999，82：648-651.

［6］ JING Z，YANG J，FENG W.Bifurcation and chaos in neura1 excitab1e system［J］.Chaos，So1itons and Fracta1s，2006，27：197-215.

［7］ LIU C，TIAN Y.E1iminating osci11ations in the Internet by time-de1ayed feedback contro1［J］.Chaos，So1itons and Fracta1s，2008，35：878-887.

［8］ RAMESH M，NARAYANAN S.Chaos contro1 of Bonhoeffer-van der Po1 osci11ator using neura1 networks［J］.Chaos，So1itons and Fracta1s，2001，12：2395-23405.

［9］ WANG J，CHEN L，FEI X.Ana1ysis and contro1 of the bifurcation of Hodgkin-Hux1ey mode1［J］.Chaos，So1itons and Fracta1s，2007，31：247-256.

［10］ WANG Z，CHU T.De1ay induced Hopf bifurcation in a simp1ified network congestion contro1 mode1［J］.Chaos，So1itons and Fracta1s，2006，28：161 -172.

［11］ ZHANG Q，WEI X，XU J.Stabi1ity of de1ayed ce11u1ar neura1 networks［J］.Chaos，So1itons and Fracta1s，2007，31：514-520.

［12］ OMEL O E，CHENKOA B C，HAUPTMANNB C.Co11ective dynamics of g1oba11y coup1ed phase osci11ators under mu1tisite de1ayed feedback stimu-1ation［J］.Physica D，2008，237：365-384.

［13］ RINA S，CHUNRUI Z，ZUOLIN S.Stabi1ity Ana1ysis for Mutua11y De1ay-coup1ed Semiconductor Lasers System［J］.Abstract and App1ied Ana1ysis，2013，Artic1e ID：248379.

［14］ 苏日娜.具时滞耦合微分系统的动力学性质［D］.哈尔滨：东北林业大学，2014.

责任编辑：时 凌

The StabilitY of GloballY CouPled Phase Oscillators SYstem with DelaY

SU Rina
（Co11ege of Mathematics，Inner Mongo1ia University for Nationa1ities，Tong1iao 028043，China）

Under the condition of coup1ing intensity and de1ayed feedback，a kind of g1oba11y coup1ed phase osci11ators system with time de1ay is considered.By ana1zing the distribution of the roots to the associated characteristic equation，the existence of the periodic so1ution for the system and the Hopf branch conditions are investigated.

time de1ay；coup1ed system；periodic so1ution；Hopf branch

O193

A

1008-8423（2016）02-0159-03

10.13501/j.cnki.42-1569/n.2016.06.012

2016-05-30.

苏日娜（1988-），女，硕士，主要从事时滞微分方程的研究.