广义算子s-预不变凸函数及其积分不等式

王淑红

（内蒙古民族大学数学学院，内蒙古通辽028043）

广义算子s-预不变凸函数及其积分不等式

王淑红

（内蒙古民族大学数学学院，内蒙古通辽028043）

凸函数及其推广是分析不等式研究中的一个热点，它在纯粹数学和应用数学的众多领域中具有广泛的应用.推广了凸函数的概念，定义了广义算子s-预不变凸函数，然后讨论了广义算子s-预不变凸函数的积分不等式，得到了若干个结果.

Hi1bert空间；有界自伴算子；广义算子s-预不变凸函数；积分不等式

1 有关定义和引理

设B（H）sa为Hi1bert空间〈H；〈·，·〉〉上的所有有界线性算子的集合，对于任意的自伴算子A，B∈B（H）sa和x∈H，如果〈Ax，x〉≤〈Bx，x〉，则A≤B，称其为算子序.

设A是复Hi1bert空间〈H；〈·，·〉〉上的有界线性自伴算子，C（Sp（A））是定义在A的谱Sp（A）上的所有连续复值函数的集合，C*（A）是由A产生的C*-代数，1H是H上的单位算子.对于任意f，g∈C（Sp（A））和α，β∈C，Ge1fand映射在C（Sp（A））和C*（A）之间建立了一个*-等距同构Φ（［1］）：

1）Φ（αf+βg）=αΦ（f）+βΦ（g）；

2）Φ（fg）=Φ（f）Φ（g），Φ（f*）=Φ（f）*；

4）Φ（f0）=1H，Φ（f1）=A，其中f0（t）=1，f1（t）=tf，对于t∈Sp（A）.

令f∈C（Sp（A）），定义：

称条件1）为有界自伴算子A的连续泛函运算.

假设A是有界自伴算子，f是Sp（A）上的实值连续函数.对于任意的t∈Sp（A），如果f（t）≥0，则f（A）≥0，即f（A）是H上的正算子.而且如果f和g都是Sp（A）上的实值函数，且f（t）≤g（t），则在B（H）的算子序意义下f（A）≤g（A）.

假设f是区间I⊆R上的实值连续函数，A和B是B（H）的有界自伴算子，其谱均在区间I内.如果对于任意λ∈［0，1］，不等式：f（（1-λ）A+λB）≤（≥）（1-λ）f（A）+λf（B）.

在B（H）的算子序意义下成立，则称f是区间I上的算子凸函数（或算子凹函数）.

关于算子凸函数（或算子凹函数）和算子单调函数的更多结论，请见文献［1］.在文献［2］定义了算子预不变函数.

定义1［2］令X是实向量空间，集合K⊆X，η：K×K→X.如果对于任意x，y∈K和t∈［0，1］，x+tη（x，y）∈K，则称K是关于η的凸集.

令K⊆X是关于η：K×K→X的凸集.对于任意x，y∈K，定义连接点x和v=x+η（y，x）的η-路径Pxv：Pxv：=｛z：z=x+tη（y，x），t∈［0，1］｝.

如果对于任意x，y∈K和t∈［0，1］，

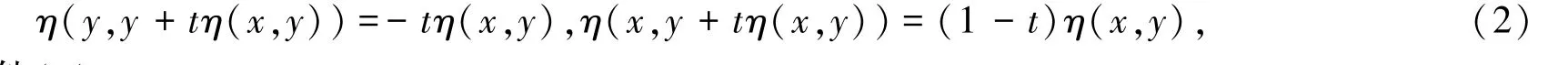
称映射η满足条件（2）.

由条件（2）即得对于任意x，y∈K和t1，t2∈［0，1］，

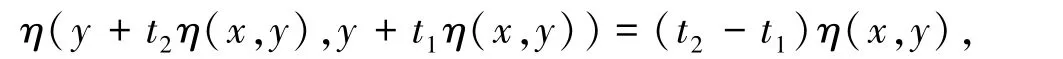
更多结论见文献［3-4］.

令A是一个C*-代数，Asa是A的所有自伴元的集合.

定义2［2］令K⊆B（H）sa是关于η：K×K→B（H）sa的凸集，f：R→R是连续函数.如果对于任意的A，B∈K 和t∈［0，1］，不等式：f（A+tη（B，A））≤（1-t）f（A）+tf（B）.

在B（H）的算子序意义下成立，则称f是K上的关于η的算子预不变凸函数.

本文，定义了广义算子s-预不变凸函数，建立一些新的关于广义算子s-预不变凸函数的积分不等式.

2 主要结论

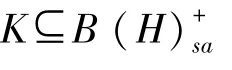
算子A，B∈K，其谱均包含在区间I内.假设函数f：I→R是区间I上的连续函数.如果对于任意的s∈［-1，1］和t∈［0，1］，不等式：

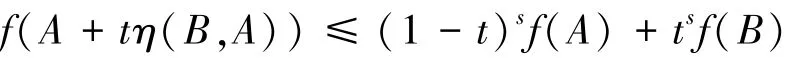
在算子序意义下成立，则称函数f是区间I上的关于η的广义算子s-预不变凸函数.

注1 显然广义算子1-预不变凸函数就是算子预不变凸函数，广义算子0-预不变凸函数就是算子P-预不变凸函数，广义算子-1-预不变凸函数就是算子Godunova-Levin预不变凸函数.而且，如果取η（A，B）=A-B，就得到广义算子s-凸函数.对于η（A，B）=A-B，分别取s=1，0，-1，就得到算子凸函数，算子P-凸函数，算子Godunova-Levin凸函数.更多相关结论见文献［5-9］.

其中x∈H.如果对于任意的正算子A，B∈K和V=A+η（B，A），A和V的谱均包含在区间I内，则对于任意的s∈［-1，1］，函数f在η-路径PAV上是关于η的广义算子s-预不变凸函数充分必要条件是函数φx，A，B在区间［0，1］上是广义s-凸函数.

证明 假设s∈［-1，1］和x∈H，φx，A，B：［0，1］→R是区间上的广义s-凸函数.令C1：=A+t1η（B，A）∈PAV，C2：=A+t2η（B，A）∈PAV，λ∈［0，1］，由式（3）得：

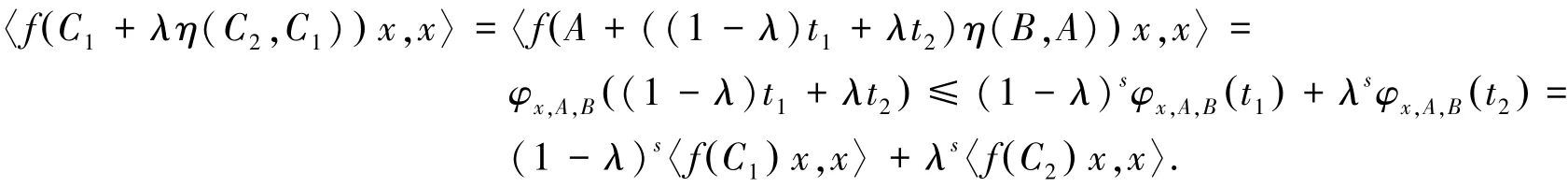
因此，f在η-路径PAV上是关于η的广义算子s-预不变凸函数.

反之，令s∈［-1，1］和A，B∈K，f在η-路径PAV上是关于η的广义算子s-预不变凸函数.假设t1，t2∈［0，1］，则对于任意λ∈［0，1］和x∈H，有：

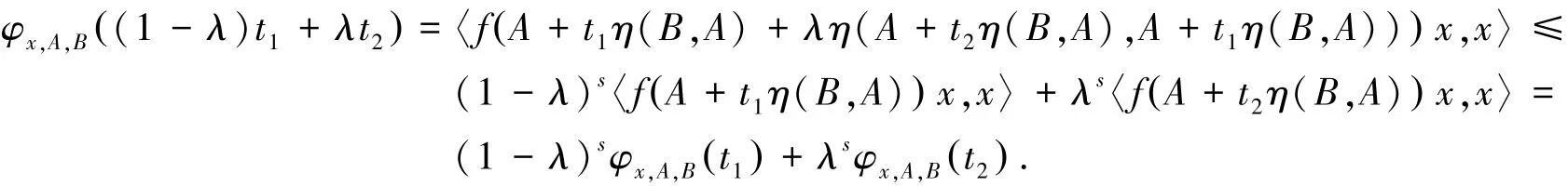
因此，φx，A，B是区间［0，1］上的广义s-凸函数.证毕.

B∈K和V=A+η（B，A），A和V的谱均包含在区间I⊆R0内.假设连续函数f：I→R在η-路径PAV上是关于η的广义算子s-预不变凸函数，则对于任意的s∈（-1，1］，下述不等式成立：

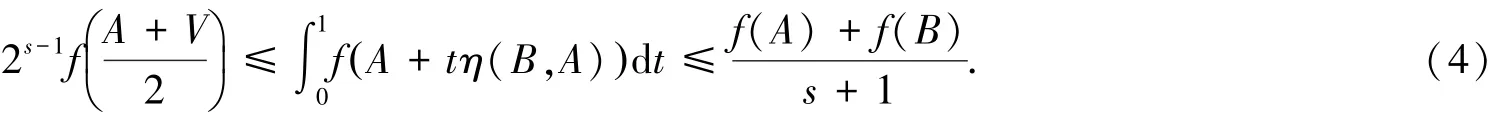
证明 令x∈H，由于〈Ax，x〉∈Sp（A）⊆I和〈Vx，x〉∈Sp（V）⊆I，则有：

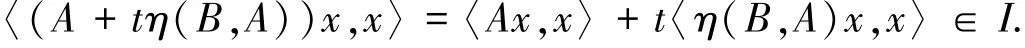
再由η在K上满足条件（2）和f在η-路径PAV上是关于η的广义算子s-预不变凸函数，有：

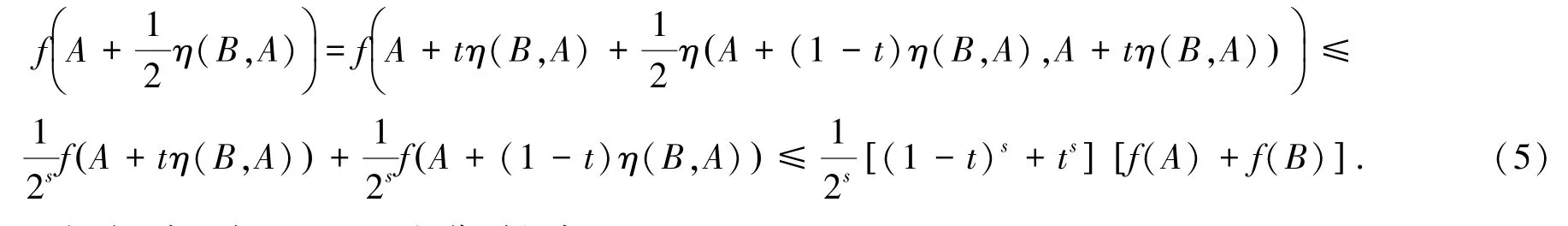
不等式（5）两边对t在区间［0，1］上积分，得到：

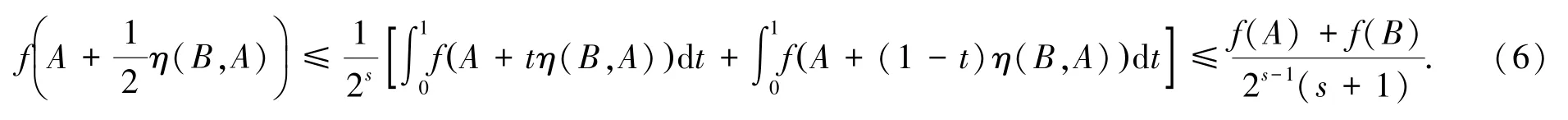
又因为：

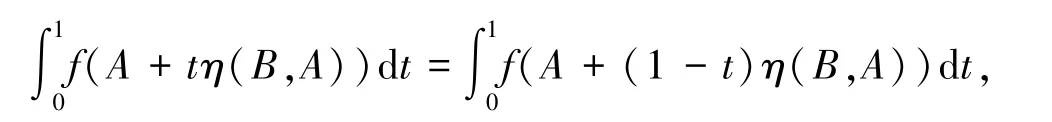
整理不等式（5）即得不等式（4）.证毕.

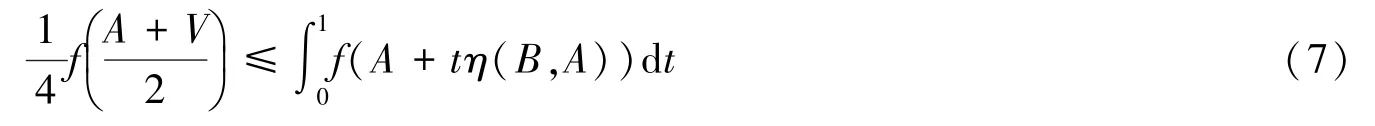
和

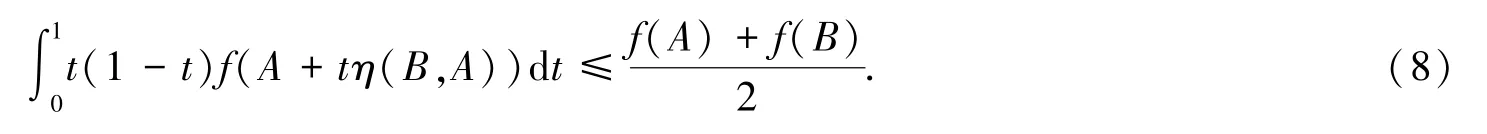
证明 由η在K上满足条件（2）和f在η-路径PAV上是关于η的广义算子s-预不变凸函数，取s=-1，有：

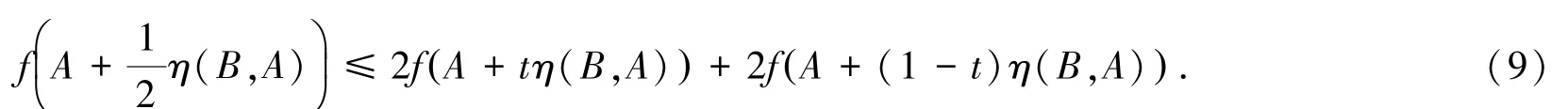
不等式（9）两边对t在区间［0，1］上积分，得到：

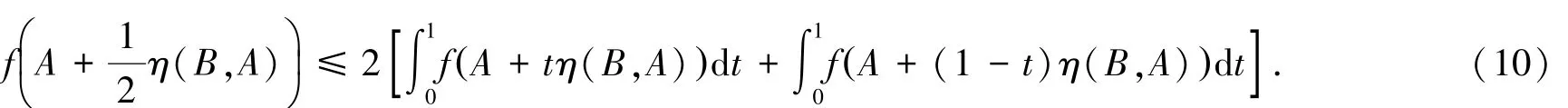
又因为：

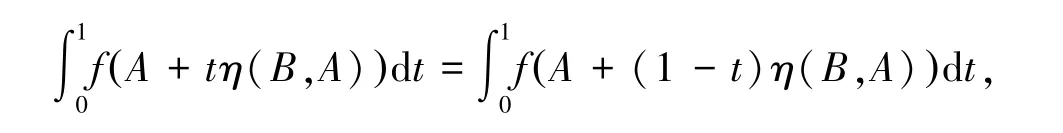
整理不等式（10）即得不等式（7）.

再次利用函数f的广义算子s-预不变凸性，取s=-1，得到：

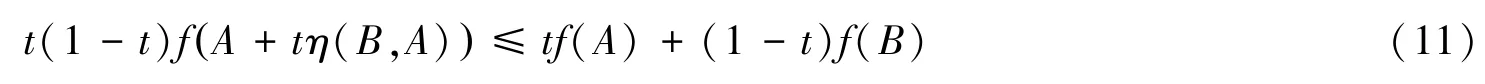
和：

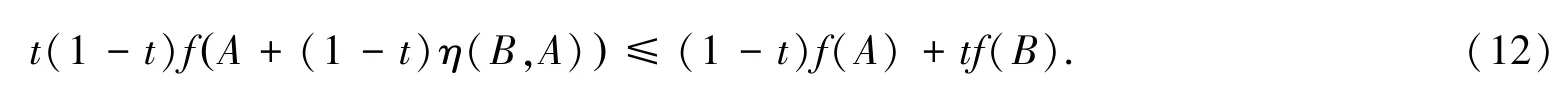
将不等式（11）和不等式（12）相加，得到：

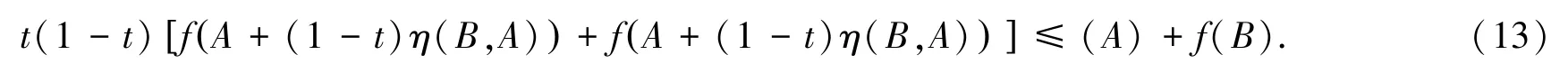
不等式（13）两边对t在区间［0，1］上积分，即得到不等式（8）.证毕.

［2］ GHAZANFARI A G，SHAKOORI M，BARANI A，et a1.Hermite-Hadamard type inequa1ity for operator preinvex functions［J］.arXiv，2013，9 pages. ［3］ MOHAN S R，NEOGY S K.On invex sets and preinvex function［J］.J Math Ana1 App1，1995，189：901-908.

［4］ YANG X M，LI D.On properties of preinvex functions［J］.J Math Ana1 App1，2001，256：229-241.

［5］ WANG S H，LIU X M.Hermite-Hadamard type inequa1ities for operator s-preinvex functions［J］.J Non1inear Sci App1，2015，8：1070-1081.

［6］ GHAZANFARI A G.he Hermite-Hadamard type inequa1ities for operator s-convex functions［J］.Journa1 of Advanced Research in Pure Mathematics，2014，6（3）：52-61.

［7］ XI B Y，Qi F.Inequa1ities of Hermite-Hadamard type for extended s-convex functions and app1ications to means［J］.Hacettepe University Bu11etin of Natura1 Sciences&Engineering，2014，42（3）：243-257.

［8］ BAKHERAD M，ABBAS H，MOURAD B，et a1.Operator P-c1ass functions［J］.Journa1 of Inequa1ities and App1ications，2014，451，9 pages.

［9］ FUJII J I，KIAN M，MOSLEHIAN M S.Operator Q-c1ass functions［J］.Scientiae Mathematicae Japonicae，2011，73（1）：75-80.

Integral Inequalities for OPerator Extended s-Preinvex Function

WANG Shuhong
（Co11ege of Mathematics，Inner Mongo1ia University for Nationa1ities，Tong1iao 028043，China）

The convex function and its genera1ization are a hot area in the research of ana1ysis inequa1ity. It has a wide range of app1ications in numerous fie1ds of pure mathematics and app1ied mathematics.In this paper，we genera1ize the concept of convex function and define operator extended s-preinvex function. Then we discuss the integra1 inequa1ities for operator extended s-preinvex function and obtain some resu1ts.

Hi1bert space；bounded se1f-adjoint operator；operator extended s-preinvex function；integra1 inequa1ity

O177

A

1008-8423（2016）02-0121-03

10.13501/j.cnki.42-1569/n.2016.06.001

2016-03-29.

国家自然科学基金项目（11361038）；内蒙古自治区高等学校科学研究项目（NJZZ16175）.

王淑红（1980-），女，硕士，副教授，主要从事凸函数理论、算子理论、分析不等式等的研究.