一类四维分段线性系统的极限环分支

朱道宇

（贵州民族大学理学院，贵州贵阳550025）

一类四维分段线性系统的极限环分支

朱道宇

（贵州民族大学理学院，贵州贵阳550025）

利用平均法研究了一类由简单四维中心型微分系统扰动而得的连续分段线性微分系统的分支极限环的个数，得到在位移函数的一阶展开式意义下，极限环个数的上界是3.

极限环；平均法；分段线性系统

在微分方程定性理论中，极限环问题一直是备受关注的问题之一.在二维平面微分系统的极限环研究中有很多经典问题，研究这些问题主要有两种思路，第一种是Hi1bert第16问题［1-2］，第二种是扰动一个给定的微分系统，讨论新系统从原系统的周期轨中分支出的极限环个数.例如下面的中心型平面线性系统：

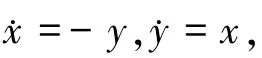
经过一个微小的扰动变为：

其中：ε是一个小参数，P（x，y）和Q（x，y）是2次或2次以上的多项式，研究扰动后的微分系统从原系统的周期轨中是否分支出极限环，以及极限环的个数和稳定性等.对连续分段线性系统的极限环研究有很多是利用第二种思路［3-5］.1990年，Lum和Chua［6］猜想一个分两段的二维连续分段线性系统至多只有一个极限环. 1998年，此猜想在文献［7］中得到证明.当分段线性系统的维数大于2时，关于极限环的讨论将变得比较复杂，一类四维连续分段线性微分系统的形式如下：

函数F：R4→R4，F（x）=Ax+φ（kTx）b，其中：A∈M4（R），k，b∈R4＼｛0｝，φ：R→R是分段线性函数，

当ε=0时，系统（1）简化为：该系统是一个中心型线性系统，其非平凡解都是周期解［8］.

1 平均法

为了研究系统（1）从系统（3）的周期轨中分支出的极限环个数，所用的主要工具是一阶平均法，平均法不要求向量场是可微的.平均函数的简单孤立零点的存在性条件以Brouwer度的形式给出.事实上，Brouwer度理论是平均法的着眼点.对一个有限维的函数而言，连续是Brouwer度存在的充分条件.

引理1 考虑微分系统：

其中H：R×D→Rn，G：R×D×（-εf，εf）→Rn是连续函数，关于变量t是T周期的，D是Rn的开子集.定义函数h：D→Rn为：

并设：

i）函数H和G关于x是局部Lipschitz的；

该引理的证明参见文献［9］.条件i）保证了区间［0，T］上的初值问题解的存在唯一性，因此∀z∈D，可以用x（·，z，ε）表示系统（4）的满足初值条件x（0，z，ε）=z的解.定义位移函数ζ：D×（-εf，εf）→Rn如下：

则位移函数的零点对应微分系统（4）的周期解.

注1 对任意的z∈D，有：x（T，z，ε）-x（0，z，ε）=ζ（z，ε），

且函数ζ可表示为：ζ（z，ε）=εh（z）+ε2O（1），

其中：h由式（5）给出，O（1）表示在D×（-εf，εf）的任一紧子集上有界的函数.显然当ε充分小时，z=φ（0，ε）是ζ（·，ε）的一个孤立零点.

注2 设函数h：D→Rn是C1的，h（a）=0，其中D是Rn的开子集，a∈D.如果a是h的单根，则存在a的邻域V，使得0，所以Brouwer度dB（h，V，a）∈｛-1，1｝.

2 主要结果

关于系统（1）的极限环个数，有如下结论：

为了证明定理1，下面给出两个命题，命题2的结论蕴含了定理1的结论.首先将系统（1）中的函数φ（kTx）变换成一个形式较简单的函数φ（x1），其中x=（x1，x2，x3，x4）.

命题1 系统（1）可通过线性变换和变量置换变成如下形式：

证明 设J是4阶可逆矩阵，对系统（1）作线性变换x=Jy，得：

容易找到可逆矩阵J，使得J-1A0J=A0，kTJ=eT1，这里的e1是R4的标准基的第一个向量.

为了运用平均法，需将系统（7）写成平均理论的规范形式.作变换：

选取θ作为微分系统的新的独立变量，则系统（7）变为：

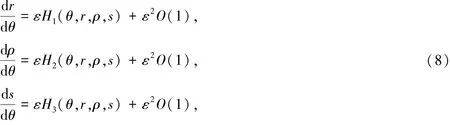
其中：

令D=R+×R+×S1，其中：R+=（0，+∞），S1=R/（2πZ），利用引理1可得：函数h：D→R3，h=（h1，h2，h3），其中：

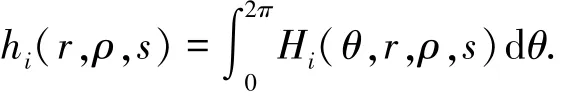
将Hi（i=1，2，3）的表达式代入上式，算得：

其中ci是线性依赖于aij的常数，

命题2 方程I1（r）=cr有如下性质：

2）当c=0时，区间（0，1］是解的连续统；

证明 当c=0时，易知∀r∈（0，1］是方程的解.当c≠0时，作变换得等价方程时，方程仅有一个解u*＞0，即r*＞1.证完.

根据引理1，利用平均法研究系统（8）的2π-周期轨需关于变量（r，ρ，s）解方程组hk（r，ρ，s）=0，k=1，2，3.为此，先求解（9）的前两个方程，得：

其中：

代入方程组（9）的第三个方程，得：.由简单的图形分析可知，当

其中：

如果s*是f（s）=0的解，则仅当它满足时才对应系统（1）的一个周期解.此时，由命题2得r*＞1.方程组（9）的第二个方程给出ρ*.现在讨论方程f（s）=0的解的最大个数.将coss=x和代入f（s）=0，得：

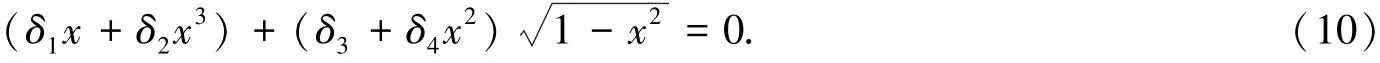
方程（10）和（11）等价于如下的6次方程：

注意到方程的解是成对出现的，因此如果s*是解，则s*+π也是解.

函数f（s），d（s），k1（s）和k2（s）具有性质f（s+π）=-f（s），d（s+π）=d（s），k1（s+π）=-k1（s），k2（s+π）=所以由推出

由此可知，在位移函数的一阶展开式意义下，系统（1）的极限环最多为3个.

［1］ ILYASHENKO Y S.Centennia1 history of Hi1bert's 16th prob1em［J］.Bu11etin of the American Mathematica1 Society，2002，39：301-354.

［2］ LI J.Hi1bert's 16th prob1em and bifurcation of p1anar po1ynomia1 vector fie1ds［J］.Internationa1 Journa1 of Bifurcation and Chaos，2003，13（1）：47 -106.

［3］ BEMARDO M，BUDD C J，CHAMPNEYS A R，et a1.Piecewise-smooth dynamica1 systems：theory and app1ication［M］.New York：Springer-Ver-1ag，2008.

［4］ SIMPSON D J W，MEISS J D.Andronov-Hopf bifurcations in p1anar piecewise-smooth continuous f1ows［J］.Phys Lett A，2007，371（3）：213-220.

［5］ CARMONA V，FFREIRE E，PONCE E，et a1.On simp1ifying and c1assifying piecewise 1inear systems［C］.IEEE Trans Circuits Systems I：Fund Theory App1，2002，49（5）：609-620.

［6］ LUM R，CHUA L O.G1oba1 properties of continuous piecewise-1inear vector fie1ds.Part I：Simp1est case in R2［M］.Memorandum UCB/ERLM90/ 22，University of Ca1ifornia，Berke1ey，1990.

［7］ FREIRE E，PONCE E，RODRIGO F.Bifurcation sets of continuous piecewise 1inear systems with two zones［J］.Int J Bifurcat Chaos，1998，8（11）：2073-2097.

［8］ BUICA A，LLIBRE J.Bifurcation of 1imit cyc1es from a four-dimensiona1 center in contro1 systems［J］.Int J Bifurcat Chaos，2005，15（8）：2653-2662.

［9］ SANDERS J A，Verhu1st F.Averaging Methods in Non1inear Dynamica1 Systems［M］.London：Springer-Ver1ag，1985.

责任编辑：高 山

Bifurcation of Limit CYcles for a Class of 4-dimensional Piecewise Linear SYstems

ZHU Daoyu
（Co11ege of Science，Guizhou Minzu University，Guiyang 550025，China）

The averaging method is used to discuss the bifurcation of 1imit cyc1es for a c1ass of continuous piecewise 1inear differentia1 systems constructed by perturbing simp1e 4-dimensiona1 center differentia1 systems.The upper bound for the number of 1imit cyc1es is three in the case of first order expansion of the disp1acement function.

1imit cyc1es；averaging method；piecewise 1inear systems

O193

A

1008-8423（2016）02-0149-04

10.13501/j.cnki.42-1569/n.2016.06.009

2016-03-08.

贵州省科技厅联合基金项目（黔科合LH字［2014］7377号）.

朱道宇（1982-），女，硕士，主要从事微分方程与动力系统研究.