极端波浪条件下黏土质斜坡海床稳定性解析

年廷凯，刘 敏，刘 博，郑德凤，宋 雷，印 萍

(1. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024；2. 辽宁师范大学 城市与环境学院, 辽宁 大连 116029；3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221008；4. 国土资源部海洋油气资源与环境地质重点实验室, 山东 青岛 266071)

极端波浪条件下黏土质斜坡海床稳定性解析

年廷凯1，刘 敏1，刘 博1，郑德凤2，宋 雷3，印 萍4

(1. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024；2. 辽宁师范大学 城市与环境学院, 辽宁 大连 116029；3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221008；4. 国土资源部海洋油气资源与环境地质重点实验室, 山东 青岛 266071)

海洋资源开发引起海底软黏土的结构性破坏，导致土体强度弱化，在百年一遇的极端波浪作用时极易发生斜坡海床的局部失稳甚至大范围海底滑坡，给海洋工程建设和正常运营带来严重影响。目前，主要采用极限平衡法评价这类海底斜坡，但该法只能给出近似解。基于极限分析上限方法，推导了极端波浪诱发的波压力对斜坡海床的做功功率，建立了外力功与内能耗散率平衡方程；利用最优化方法，结合数值积分和强度折减技术，求解了不同时刻的斜坡海床稳定性系数，并针对扰动后的斜坡海床开展了有限元解的对比验证。在此基础上，深入探讨了不同波浪参数(波长、波高和水深)和坡长小于一个波长等极端条件下的海底斜坡稳定性。

海底滑坡；斜坡稳定性；极限分析上限方法；波浪荷载；数值积分技术

Abstract: The shear strength of soft clay in sloping seabed will be weakened due to the structure failure induced by marine resource exploration. Under extreme wave loads once a hundred years, local slide or even large-scale landslide will happen in the seabed. This will influence greatly the construction and normal operation of ocean engineering. Currently, the limit equilibrium method (LEM) has been one of the most popular approaches to assess the whole or local stability of clayey sloping seabed. But the method has some limitations and only the approximate solutions can be obtained. Based on the upper bound approach of limit analysis, the paper derives the external work rates produced by the wave-induced pressure on the sloping seabed. The limit state equation of sloping seabed under wave loading is established through the external work rates being equal to the internal energy dissipation rates along the log-spiral sliding surface. The factors of safety (FS) at the different time under one-wave period are obtained by using the optimization method combined with numerical integration and strength reduction technique. A representative example is employed, and the analytical solutions of stability for the disturbed sloping seabed under wave loading are verified by comparison of the finite element results. On this basis, the stability of clayey sloping seabed under extreme conditions such as various wave parameters (i.e., wave length, wave height and water depth) and the special case of slope length no more than one wave length are discussed in detail.

Keywords: seafloor slide; slope stability; upper bound approach of limit analysis; wave loads; numerical integration technique

近年来，全球范围内海洋石油开发、天然气水合物开采、海底管线铺设、人工岛礁建设等海洋工程活动日益频繁，由此对工程活动区较大范围内的斜坡海床软黏土造成了一定影响[1-6]。一般地，软黏土具有一定的触变性，当其结构受到扰动后在短期内呈现强度弱化或软化效应[7-9]，强度显著下降，当偶遇极端波浪荷载极易诱发斜坡海床发生局部滑动甚至大规模海底滑坡，从而威胁海洋工程安全甚至造成海洋基础设施的严重破坏。如美国卡米尔飓风引发的海底软土层滑移[6]，造成海洋平台翻倒并沿斜坡向下滑出30 m，造成部分海底电缆和管道断裂。因此，开展极端波浪条件下强度弱化后的黏土质斜坡海床稳定性评价具有重要的现实意义。

目前，斜坡海床稳定性评价主要采用极限平衡法。Henkel[10]最早采用圆弧破坏模式、滑体力矩平衡法对一阶波浪荷载下无限斜坡海床进行了稳定性研究；顾小芸[11]采用同样的方法对浙江象山港近东海区域黏质海底稳定性进行了分析；宋连清等[12]采用总应力极限平衡法，分析了地震及波浪荷载对岙山成品码头斜坡海床稳定性的影响；孙永福等[13]基于极限平衡思想，开发Geo-Slope软件，对风暴潮作用下黄河水下三角洲双层斜坡海床的稳定性进行了深入分析。但上述各类极限平衡法没有考虑坡体水平向应力状态对斜坡海床稳定性的影响，刘晓丽等[14]考虑坡体水平向应力状态，针对波浪作用下缓倾角海底无限坡提出了基于滑动面处土体应力状态的滑动稳定性计算方法，进一步丰富了极限平衡法。然而极限平衡法因引入了滑动面形状和位置及条间力关系的若干假定，其结果仍然是一种近似解答。

Chen[15]将塑性极限分析方法引入边坡稳定性评价中，由于其采用的对数螺旋面转动破坏模式接近实际，且能够考虑浅层或深部滑动，既满足精度要求也能给出真实解，故在水下斜坡的稳定性分析中得到了快速发展。如Viratjandr & Michalowski[16]对水下斜坡进行了变动水位条件下的上限极限分析，并提出图表解；安晨歌等[17]基于极限分析上限法，探究了天然气水合物分解形成的软弱夹层对海底缓坡稳定性的影响；刘博[18]将一阶正弦波在一个波浪周期内进行分段线性化，开展了波浪作用下的海底斜坡稳定性上限分析，由于其对波压力的简化处理，结果仍存在一定的误差。鉴于上述问题，本文考虑真实的波压力和极端波浪条件，针对强度弱化后的黏土质斜坡海床开展了极限分析上限法研究，并探究斜坡长度不超过一个波长的特殊斜坡海床。

1 极限分析上限方法基本理论

极限分析上限法是以塑性力学中的静力学和运动学定理为基础，假定土体满足一定的破坏准则和流动法则，在给定破坏模式(如对数螺旋线)条件下，令外力功率与内能耗散功率相等建立临界状态方程，从而得到实际问题的一个上限解，对于边坡问题即为临界高度或安全系数，如下：

2 斜坡海床稳定性的上限方法

根据已有成果[1]，海底斜坡的破坏模式大致可分为：滑动、倾倒、扩张、坠落、流动；滑动又可分为平移滑动与旋转滑动。对于黏土质斜坡海床而言，旋转滑动是最常见的整体破坏模式。基于此，假定黏土质斜坡海床的破坏模式为对数螺旋面，已有结果表明[15-17]，这种破坏模式更接近实际。对数螺线方程为

式中：r0为对数螺旋滑动面的基线；θ0为滑动基线与水平面的夹角；r为旋转中心与滑动面上任意一点的连线即极径，任一极径与水平面的夹角为θ；φ为土体的内摩擦角。

基于极限分析上限法来研究斜坡海床的稳定性，海床土体应满足一定的假定条件：1)土体为刚塑性体；2)土体破坏时满足Mohr-Coulomb屈服准则；3)土体服从相关联流动法则。图1建立了波浪荷载作用下斜坡海床的破坏机构。

图1所示刚体ABDC绕着中心O(待定)点以角速度Ω相对对数螺旋面BD以下的静止斜坡体做平面刚体转动，H、β分别表示斜坡的高度及坡角；β′为AD与水平方向的夹角；rh为OD的长度，其与水平面的夹角为θh；L和S分别表示AB和CD的长度；V为根据相关流动法则确定的虚拟速度场，表达式为

式中：V0为B点所在速度间断面的速度矢量；H、L和S可无量纲化，转化为关于θ0、θh和β′的函数[18]。

2.1 斜坡海床外力做功功率

1)自重做功功率

根据图1所示的旋转破坏机构，海底斜坡ABCD在自重下的做功功率为

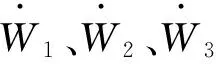
2)波浪对斜坡海床做功功率

波浪对斜坡海床的做功功率，由波浪对其下方的海床波压力产生(图2)。对于强度弱化后的黏土质斜坡海床，在波压力与重力双重作用下，极易发生海底滑坡。根据已有成果[10-14]，当海底坡度小于20°时，波浪引起的海床波压力[11]可采用一阶线性波压力公式

式中：λ为波数，可表示为λ=2π/Lw；x是计算点处的水平位置坐标(A点为圆心，水平线为x轴，向右为正)；t是计算时刻；ω是波浪的圆频率，可表达为ω=2π/T，T为波浪周期；Hw和d分别表示波高和计算点水深；γw为海水重度。

图1 波浪条件下斜坡海床的破坏机构Fig. 1 The failure mechanism of sloping seabed under wave condition

图2 波浪作用斜坡海床的波压力分布Fig. 2 The wave pressure distribution of sloping seabed under waves

任意时刻波浪力做功的功率可表达为

式中：vi表示滑体上界面DCAB上的运动速度，其它参数的意义同上。

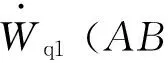
式中：fq1、fq2和fq3可分别表达为：

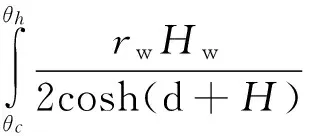
基于上述分段表达的斜坡海床波浪力功率，得任意时刻波浪力做功的总功率为

式中：fq1、fq2和fq3由复化Simpson数值积分法求解[19]。

综上所述，波浪作用下斜坡海床总的外力做功功率表达为

2.2 斜坡海床内能耗散率

整个滑体以对数螺线模式绕O点发生刚塑性转动，故系统的内能损耗只发生在速度间断面上，即图1中的对数螺线滑动面BD，则沿该面的内能耗散率可表达为

2.3 功能平衡方程及优化求解

式中：H是关于θ0、θh和β′的函数；当β=β′时，f4为0，此时对数螺线滑动面恰好通过坡趾处。

为求解斜坡海床的稳定性系数，引入强度折减技术[20]，即定义一个折减系数FS，对海床黏土的抗剪强度进行折减，折减后的抗剪强度参数可分别表达为

式中：c和φ分别为扰动后的黏土黏聚力和内摩擦角，cm和φm为折减后的强度指标。将式(13)代入式(12)，经简化、变换，即可得到安全系数FS关于独立变量θ0、θh和β′的隐式方程:

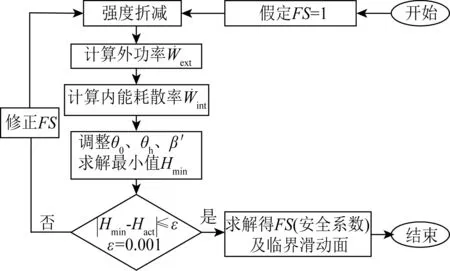
图3 斜坡海床稳定性系数优化求解流程Fig. 3 Flow chart for solving the stability safety factor of sloping seabed

式中：系数f1～f4及fq1～fq3中的c和φ均由cm和φm替换。上述工作的具体求解思路如图3所示，基于Visual Fortran语言开发了相应的优化求解程序，实现了复杂环境下斜坡海床的稳定性评价。需要说明，这里将波浪力等效为拟静力荷载，在一个波浪传播周期内平均取八个时间节点，分别记为t1～t8时刻(其时间间隔为T/8，T是波浪传播周期)，计算这八个不同时刻的波浪力作用下斜坡海床稳定性系数，取最小值为该波浪条件下斜坡海床的稳定性安全系数。

3 方法验证

算例：某斜坡海床[18]，坡角为β=5°，坡高为H=15 m，主要由软黏土构成，其饱和重度γ=18 kN/m3，初始抗剪强度参数为φ=2.53°和c=24 kPa。考虑工程扰动对土体强度的弱化效应，将黏聚力和内摩擦角以25%进行折减，折减后的强度指标为：φ=1.9°，c=18 kPa。考虑波压力与重力的双重作用，取计算水深为8 m，以波长和波高分别为Lw=30 m和Hw=2.5 m；Lw=60 m和Hw=5 m两种工况，采用图3所示的求解过程开展斜坡海床稳定性的对比验证。

两种工况下斜坡海床稳定性的极限分析上限解与有限元解如图4所示。对比可见，本文解与有限元解很接近，差值均在 2%以内。此外，两种方法计算的稳定性安全系数随时间的波动趋势也几乎一致，最小稳定性安全系数均是在相同时刻获得，由此表明本方法是合理有效的。

图4 两种方法获得的斜坡海床稳定性系数对比Fig. 4 Comparison of the safety factors of sloping seabed by two methods

4 极端工况讨论

4.1 极端波浪影响分析

对于极端波浪作用下的斜坡海床，波高、波长和水深是影响稳定性的重要因素。为了进一步揭示波浪参数对斜坡海床稳定性的影响规律，针对上述算例开展了不同波浪参数下的斜坡海床稳定性分析。

图5给出了水深8 m条件下，波长和波高分别为Lw=40 m和Hw=2.5 m、Lw=80 m和Hw=2.5 m及Lw=80 m和Hw=5 m三种工况下的斜坡海床稳定性系数随时间的变化曲线。分析可见，不同海况条件下斜坡海床的稳定性系数均随着时间围绕静水条件下的稳定性安全系数(图5中虚线所示1.650)上下波动，而且随着波高、波长的增大波动越来越剧烈。对比分析图5(a)与(b)，后者的最小稳定性安全系数比前者降低了3%，说明波长增大，斜坡海床的稳定性系数下降；最小稳定性安全系数与各自静水条件下的稳定性安全系数相比，分别降低1%和3.8%，说明波长对斜坡海床稳定性的影响较小。对比图5(b)与(c)发现，后者的最小稳定性安全系数比前者降低了3.8%，说明波高增大，斜坡海床的稳定性系数降低；但后者的最小稳定性安全系数比静水条件下的稳定性安全系数降低了7.5%，说明波高的影响较为明显。综上所述，在特定水深条件下，波浪越大(波高和波长)对斜坡海床稳定性的影响越显著，特别是在极端波浪条件下更应给予关注。

图5 稳定性系数随计算时刻变化曲线Fig. 5 The FSs changing with the period of wave

图6显示Lw=80 m和Hw=5 m工况下，水深对海底斜坡稳定性系数的影响。分析可见，随着水深d的增加，安全系数随计算时间的变化曲线总体波动幅度降低；但在一个波浪周期内，最小安全系数明显增加。与静水条件下的安全系数(图6中点画线)对比，不同水深条件下的最小安全系数降低幅度不明显，最大不超过5%(图6(a))，这表明水深对斜坡海床稳定性的影响不显著，特别是随着水深增加，波浪对斜坡海床稳定性的影响逐渐减弱直至消失。

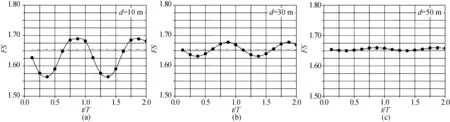
图6 水深对稳定性系数的影响Fig. 6 The effect of water depth on the stability FSs

4.2 坡长小于一个波长工况分析

仍以上述黏质斜坡海床为例，针对Lw=80 m和Hw=5 m极端海况条件，对海底斜坡坡长小于一个波长工况(L=Lw、3Lw/4、Lw/2、Lw/4四种工况)进行稳定性上限分析，计算结果列于表1。分析可见，对于给定的斜坡长度，任一时刻的斜坡稳定性系数均小于静水条件下的计算结果，且最大降幅未超过9%，这比4.1节极端波浪条件下的计算结果略高，但总体上仍显示一致性。从表中亦可发现，对于某一计算时刻，斜坡海床的稳定性系数随着坡长的增加而显著减小，这表明当海底斜坡长度小于一个波长时坡长对稳定性影响显著，应引起重视。

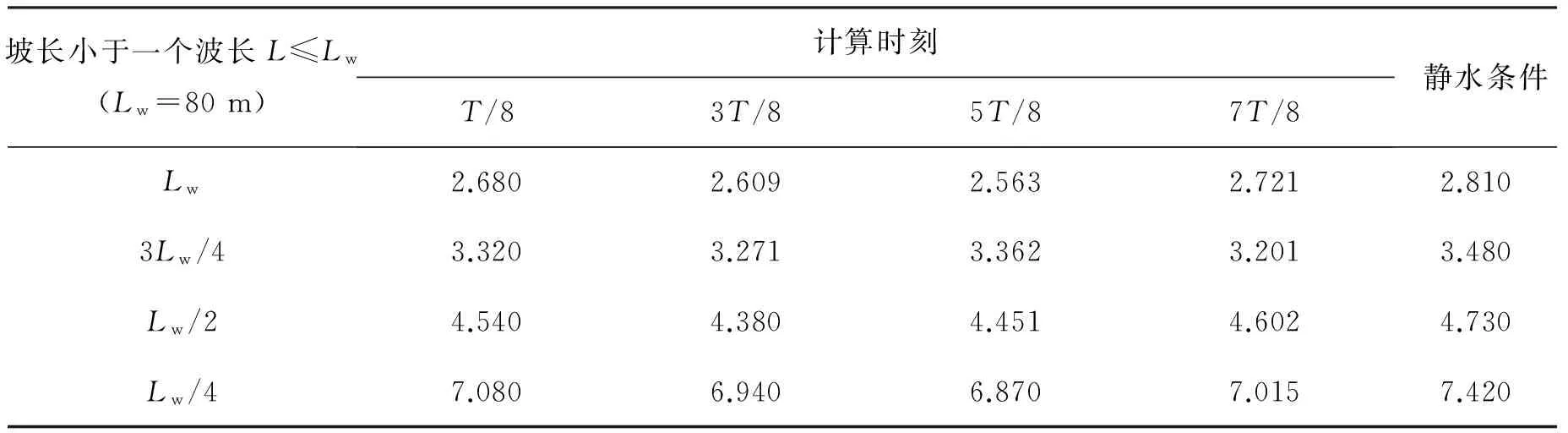
表1 海底斜坡坡长对稳定性的影响Tab. 1 The influence of length of submarine slopes on the stability FSs

5 结 语

基于极限分析理论，引入数值积分和强度折减技术，发展了极端波浪条件下黏土质斜坡海床稳定性的极限分析上限方法，并结合典型算例验证了其可行性。通过计算分析和深入讨论，得出以下几点结论：

1)对于海底斜坡长度小于一个波长工况，其稳定性随着坡长的增加而显著减小，应引起关注；

2)波高和波长对斜坡稳定性影响显著，在极端波浪条件下对稳定性安全系数的影响幅度可达9%；

3)本文考虑极端波浪条件下斜坡海床的整体失稳，未来将加强局部失稳的稳定性评价。

本项研究为波浪条件下的斜坡海床稳定性评价提供了思路，对海底滑坡的长期预测预报也有一定的参考意义。

[1] LOCAT J, LEE H J. Submarine landslides: advances and challenges[J]. Canadian Geotechnical Journal, 2002, 39(1): 193-212.

[2] 蔡正银, 陈海军, 张桂荣, 等. 波浪荷载作用下滩海人工岛工程稳定性评价[J]. 水利学报, 2007, S1: 220-225. (CAI Zhengyin, CHEN Haijun, ZHANG Guirong, et al. The artificial island project stability evaluation under waves[J]. Journal of Hydraulic Engineering, 2007, S1: 220-225. (in Chinese))

[3] 张亮. 栾锡武. 南海北部陆坡稳定性定量分析[J]. 地球物理进展, 2012, 27(4): 1443-1553. (ZHANG Liang, LUAN Xiwu. Quantitative analysis of submarine slope stability on the northern slope of the South China Sea [J]. Progress in Geophysics, 2012, 27(4): 1443-1553. (in Chinese))

[4] LEYNAUD D, MIENERT J, NADIM F. Slope stability assessment of the helland hansen area offshore the mid-norwegian margin[J]. Marine Geology, 2004, 213(1): 457-480.

[5] 刘红军, 张民生, 贾永刚, 等. 波浪导致的海床边坡稳定性分析[J]. 岩土力学, 2006, 27(6): 986-990. (LIU Hongjun, ZHANG Minsheng, JIA Yonggang, et al. Analysis of seabed stability under wave loading[J]. Rock and Soil Mechanics, 2006, 27(6): 986-990. (in Chinese))

[6] 顾小芸. 海底边坡稳定分析方法综述[J]. 力学进展, 1989, 19(1): 50-59. (GU Xiaoyun. Overview of stability analysis method of submarine slopes[J]. Advances in Mechanics, 1989, 19(1): 50-59. (in Chinese))

[7] 刘添俊, 葛修润, 安关峰. 单向循环荷载作用下饱和软黏土的性状研究[J]. 岩石力学与工程学报, 2012, 31(S1):3345-3351. (LIU Tianjun, GE Xiurun, AN Guanfeng. Study of characteristics of saturated soft clay under uniaxial cyclic load[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(S1): 3345-3351. (in Chinese))

[8] 郑刚, 霍海峰, 雷华阳. 循环荷载后原状与重塑饱和粉质黏土不排水强度排水性研究[J]. 岩土工程学报, 2012, 34(3):400-408. (ZHENG Gang, HOU Haifeng, LEI huayang. Undrained strength characteristics of saturated undisturbed and remolded silty clay after cyclic loading[J]. Chinese Journal of Geotechnical Engineering , 2012, 34(3):400-408. (in Chinese))

[9] 王元战, 焉振. 循环荷载下天津软粘土不排水强度弱化模型研究及应用[J]. 天津大学学报, 2015, 48(4):347-354. (WANG Yuanzhan, YAN Zhen. Research on and application of undrained strength softening model of Tianjin soft clay cyclic loading[J]. Journal of Tianjin University, 2015, 48(4):347-354. ( in Chinese))

[10] HENKEL D J. The role of waves in causing submarine landslides[J]. Geotechnique, 1970, 20(1):75-80.

[11] 顾小芸. 粘质海底稳定性实例分析[J]. 工程地质学报, 1996, 4(1): 32-38. (GU Xiaoyun. Case study of clayed seabottom stability[J]. Journal of Engineering Geology, 1996, 4(1): 32-38. (in Chinese))

[12] 宋连清, 叶银灿, 陈锡土, 等. 岙山成品油码头斜坡海床稳定性研究[J]. 东海海洋, 1999, 17(1): 28-36. (SONG Lianqing, YE Yinchan, CHEN Xitu, et al. Research of submarine slope stability in Ao Shan oil wharf[J]. Dong Hai Marine Science, 1999, 17(1): 28-36. (in Chinese))

[13] 孙永福, 董立峰, 蒲高军, 等. 风暴潮作用下黄河水下三角洲斜坡稳定性研究[J]. 工程地质学报, 2006, 14(5): 582-587. (SUN Yongfu, DONG Lifeng, PU Gaojun, et al. Stability analysis of slopes in the subaqueous delta of the Yellow River under storm wave loading[J]. Journal of Engineering Geology, 2006, 14(5): 582-587. (in Chinese))

[14] 刘晓丽, 窦锦钟, 英姿，等. 波致海底缓倾角无限坡滑动稳定性计算分析[J]. 海洋学报, 2015, 37(3): 99-105. (LIU Xiaoli, DOU Jinzhong, YING Zi, et al. Computational analysis of waves induced angled infinite slope sliding[J]. Acta Oceanologica Sinica, 2015, 37(3):99-105. (in Chinese))

[15] CHEN W F. Limit analysis and soil plasticity[M]. Elsevier Science Publishing Company, 1975.

[16] VIRATJANDR C, MICHALOWSKI R L. Limit analysis of submerged slopes subjected to water drawdown[J]. Canadian Geotechnical Journal, 2006, 43(8): 802-812.

[17] 安晨歌, 张建红, 周敏, 等. 基于能量上限法的海底缓边坡滑坡机理分析[J]. 西北地震学报, 2011, 33(增刊):105-109. (AN Chenge, ZHANG Jianhong, ZHOU Min, et al. Landslide mechanism of gentle seabed slope based on energy limit method[J].Northwestern Seismological Journal, 2011, 33(S):105-109. (in Chinese))

[18] 刘博. 波浪作用下海底斜坡稳定性的极限分析上限法与数值分析[D]. 大连: 大连理工大学, 2014. ( LIU Bo. Upper bound approach of limit analysis and FE numerical analysis of stability of submarine slope considering the wave-induced pressure[D]. Dalian: Dalian University of Technology, 2014.(in Chinese))

[19] 何光渝，高永利. Visual Fortran常用数值算法集[M]. 北京: 科学出版社, 2002. (HE Guangyu, GAO Yongli . The common numerical algorithm set of Visual Fortran[M]. Beijing: Science Press, 2002. (in Chinese))

[20] 许文锋, 车爱兰, 王治, 等. 地震荷载作用下海底滑坡特征及其机理[J]. 上海交通大学学报, 2011, 45(5): 782-786.(XU Wenfeng, CHE Ailan, WANG Zhi, et al. Destruction characteristic of seabed landslide during earthquake motion and its mechanism[J]. Journal of Shanghai Jiao Tong University, 2011, 45(5): 782-787. (in Chinese))

Stability analysis of clayey sloping seabed under extreme wave loads

NIAN Tingkai1, LIU Min1, LIU Bo1, ZHENG Defeng2, SONG Lei3, YIN Ping4

(1. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China; 2. School of Urban and Environmental Science, Liaoning Normal University, Dalian 116029, China; 3. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology，Xuzhou 221008, China; 4. Key Laboratory of Marine Hydrocarbon Resources and Environmental Geology, Ministry of Land and Resources, Qingdao 266071, China)

1005-9865(2016)04-0009-07

P736

A

10.16483/j.issn.1005-9865.2016.04.002

2015-12-02

国家自然科学基金资助项目(51579032)；海洋油气资源与环境地质重点实验室基金资助项目(MRE201304)；深部岩土力学与地下工程国家重点实验室基金资助项目(SKLGDUEK1307)

年廷凯(1971-)，男，教授，主要从事海洋岩土力学与防灾岩土工程方面的研究。 E-mail: tknian@dlut.edu.cn