半潜平台浮子式系泊系统参数优化研究

吴 澜，匡晓峰，范亚丽，王 飞，李新鑫

(1. 中国船舶科学研究中心 水动力学国家重点实验室，江苏 无锡 214082; 2. 大连船舶重工集团有限公司，辽宁 大连 116000)

半潜平台浮子式系泊系统参数优化研究

吴 澜1，匡晓峰1，范亚丽1，王 飞2，李新鑫2

(1. 中国船舶科学研究中心 水动力学国家重点实验室，江苏 无锡 214082; 2. 大连船舶重工集团有限公司，辽宁 大连 116000)

通过在系泊缆中设置浮子可以改善系泊系统性能，降低平台运动响应。建立浮子式系泊系统的数值计算模型，验证浮子式系泊系统数值计算方法，详细分析浮子设计参数(设置位置和净浮力大小)变化对系泊缆张力特性与平台运动的影响规律，并根据得到的规律选择了优化的浮子系泊系统方案。最后对优化方案进行评估，表明优化方案可以显著降低系泊中的平台水平运动，尤其是低频运动，同时系泊缆张力变化不大，仍满足安全要求。研究结果可为今后浮子式系泊系统设计提供参考。

浮子式系泊系统；半潜平台；数值模拟；模型试验，参数系化

Abstract: Inserting buoys to the mooring system can improve the performance of mooring system as well as decrease the platform motion. In this paper, the model of mooring system with buoys is introduced, the numerical simulation method of mooring system with buoys is validated, and the design parameters of buoys (location and net buoyancy ) are studied to see their influence on the mooring line tension as well as the platform motion. An optimized plan of mooring system with buoys is selected according to the conclusions made. At last the optimized plan is analyzed, and turns out to be effective in decreasing the offset, especially the low frequency part of platform, while the mooring tension does not increase obviously, still within the safety requirement. The results of this study could offer reference in designing of the mooring system with buoys.

Keywords: mooring system with buoys; semi-submersibles; numerical simulation; model test; parameters optimization

半潜平台是海洋油气开发的关键装备，系泊系统是半潜平台主要的定位方式之一[1]。在系泊缆中设置浮力器件，可减轻系泊缆重量，减小平台垂向载荷，增大系泊系统刚度，提高系泊性能。Mavrakos等[2-3]通过数值模拟和试验证明了设置浮子可改善系泊缆动力特性。Mavrakos和Chatjigeorgiou等[4]通过频域和时域的数值模拟讨论了浮子的参数(位置、净浮力和数量)对于系泊缆动力特性的改善情况，但研究过程只针对单根系泊缆，而且使用的是非耦合的方法，用系泊缆顶端正弦激励代替上方平台的运动。王道能[5]建立了浮子系缆模型，模拟了浮筒系泊系统的运动响应，但未有针对浮子设置参数对系泊系统性能的影响规律进行较为全面和更深入地讨论。

以一250 m水深半潜式平台系泊系统为研究对象，使用三维流体动力学计算软件AQWA构建单浮子系泊系统模型，应用耦合动力分析方法进行数值计算，讨论浮子设计参数(设置位置、净浮力大小)对于平台位移和系泊缆张力响应的影响规律，得到的结论可为今后浮子式系泊系统设计提供参考。

1 半潜平台浮子式系泊系统计算方法验证

1.1 模型建立

目标平台为某半潜式平台。平台包含两个水下浮筒；四个方形立柱；上层建筑；立柱间共有两根水平撑杆。平台参数如表1所示。使用AQWA软件建立的平台水动力模型如图1所示。

表1 平台状态参数Tab. 1 Main parameters of semi-submersible platform

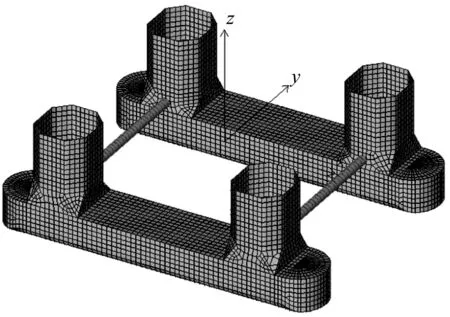
图1 半潜式平台水动力学模型Fig. 1 Hydrodynamic model of the semi-submersible

目标平台的系泊系统缆索数目为8根，对称布置。缆索水平角度为45°，张力倾角为25°，顶端预张力为577 kN 。系泊缆全部由钢缆组成，具体参数如表2所示。系泊系统布置如图2(a)所示。选取系泊浮子参数如表3所示，参考文献[6]中使用的浮子参数，浮子设置于距离系泊缆顶端317.25 m缆长的位置，提供20 t净浮力。浮子式系泊系统数值模型如图2(b)所示。

表2 系泊缆参数Tab. 2 Main parameters of mooring system

表3 浮子参数表Tab. 3 Main parameters of buoys

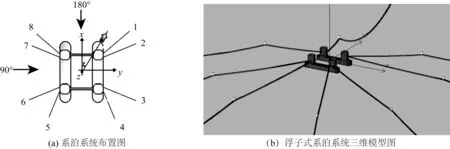
图2 系泊系统示意Fig. 2 Layout of mooring system

1.2 数值模拟方法

在ANSYS中建立平台三维水动力模型，用AQWA-LINE计算平台水动力参数及传递函数等，用AQWA-DRIFT计算平台各自由度位移时历和各缆索的张力时历等。最后使用AQWAGS进行计算结果的图形显示及后处理，对时域计算结果进行提取和统计分析[7-10]。

对于求解波浪中带有浮子的系泊系统运动时，在原系泊系统求解的基础上加入浮子的运动方程，将浮子处理为相邻两段缆索j-1和j单元连接处节点上的一个质点，可得[11]：

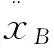
(1)

(2)

其中，xB、zB为浮筒位置坐标，MB为浮筒质量，MBa为浮筒附加质量，B0为浮筒净浮力，Ap为浮筒投影面积，cBd为浮筒阻力系数，θ为所研究的系泊缆分段的切向与水平方向夹角，T为系泊缆分段的张力，ρ为海水密度。

采用耦合动力分析系泊系统响应和平台响应时，要将系泊系统和平台系统整体考虑为动态系统联合求解[12]。

1.3 浮子式系泊系统模型试验

模型试验在耐波性水池中进行，水池主尺度为69 m×46 m×4 m(长×宽×深)，在水池相邻的两边布置了先进的三维摇板式造波机，可模拟规则波、长峰不规则波和短峰波。试验满足几何相似、运动相似和重力相似。傅汝德数和斯特洛尔数分别相等。各物理量根据相似原理按缩尺比λ换算，取λ=45。

图3 试验模型照片Fig. 3 Photos of test models

图4 单浮子系泊系统不规则波试验照片Fig. 4 Photo of mooring test with a single buoy under irregular wave

平台模型采用玻璃钢、工程塑料和木料加工而成，形状和安装位置尽量与实船保持一致重心位置、纵向及横向惯量与实体满足相似要求，缆绳采用钢丝绳模拟，浮子用塑料管加工成圆筒模拟，浮子形状和安装位置尽量与实际系泊系统保持一致，并按照所需净浮力进行配重。半潜平台及系泊浮子试验模型如图3所示。

试验选取生存工况，波浪条件的不规则波采用JONSWAP谱来模拟，波浪谱参数为：有效波高HS=8 m，谱峰周期TP=15.08 s，谱峰因子γ=1。浪向为180°顶浪。试验照片如图4所示。

1.4 数值计算与试验结果对比验证

平台运动及系泊系统受力特性试验结果与数值计算见表4、表5，计算中由于系泊系统对称性，顶浪工况下仅列出1至4号缆受力。由表可知，平台运动和系泊张力的模型试验和数值模拟结果吻合较好，说采用AQWA软件，基于时域耦合计算方法，可以较为准确的预报浮子式系泊系统的运动特性。

表4 平台运动统计值Tab. 4 Results of platform motion

表5 系泊缆张力统计值对比Tab. 5 Results of mooring line tension

2 浮子式系泊系统耦合动力分析

2.1 计算分析工况

进行浮子设计参数讨论中使用的半潜平台及系泊系统模型与上节相同。浮子尺度为高H=5.32 m，半径R=1.33 m，下面变化浮子位置和净浮力参数，讨论这两个参数的影响规律。具体分析工况：

1) 浮子位置讨论。以浮子提供5 t(约悬垂段缆重的0.2倍)和15 t(约悬垂段缆重的0.6倍)净浮力为基准，变换浮子位置分别设置在距离顶端缆长200 m、400 m、500 m、600 m、800 m处，计算相应的平台运动和系泊缆受力情况。

2) 浮子净浮力讨论。以距离顶端400 m(约0.4倍缆长)和500 m(约0.5倍缆长)位置为基准，变化浮子净浮力为5 t、10 t、15 t、20 t和25 t，计算相应的平台运动和系泊缆受力情况。

计算中只考虑180°浪向情况。在设置浮子后相应的调整系泊缆长，以保持系泊缆顶端预张力。

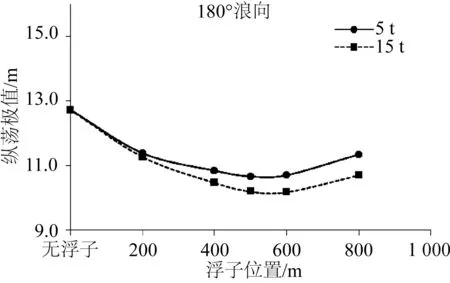
图5 平台纵荡运动极值变化曲线Fig. 5 Maximum surge of platform for different buoy locations

2.2 浮子设置位置的影响规律

由图5可知，系泊缆中设置浮子后平台纵荡极值明显降低，随着浮子设置位置距离顶端缆长的增大，平台纵荡先减小后增大，浮子设置在距离顶端缆长500 m或600 m位置时，纵荡极值最小，5 t和15 t净浮力下平台纵荡位移极值最小分别为10.66 m和10.17 m，比未设置浮子前分别降低16.19%和20.05%。

进一步分析不同波浪频率下平台纵荡运动情况，如图6所示，浮子设置后，低频运动减少较为明显，说明设置浮子对平台纵荡运动的减小作用主要靠降低平台的低频运动。随着浮子设置位置距离系泊缆顶端缆长的增大，低频有效值先减后增，其中浮子设置在距离顶端缆长400 m或500 m位置时，低频有效值最小。

图6 浮子位置不同时平台纵荡波频、低频有效值Fig. 6 Wave and low frequency significant surge value of platform for different buoy location

分析系泊系统张力特性，图7给出了180°浪向下受力最大1号系泊缆张力极值随浮子位置变化曲线，设置浮子后1号缆张力有所增大，对应系泊缆顶端张力极值约为1 580 kN，比未设浮子前增大2%，换算至系泊缆安全系数，即系泊缆破断强度和张力极值的比值为3.23，参考规范[13]，仍有较充足的安全裕量。

因而，综合考虑平台位移及系泊缆张力情况，浮子位置设在距离系泊缆顶端400 m或500 m位置，即0.4至0.5倍悬垂段缆长处，可以有效减小平台水平位移，同时满足系泊缆安全系数要求，张力响应程度不至过大。

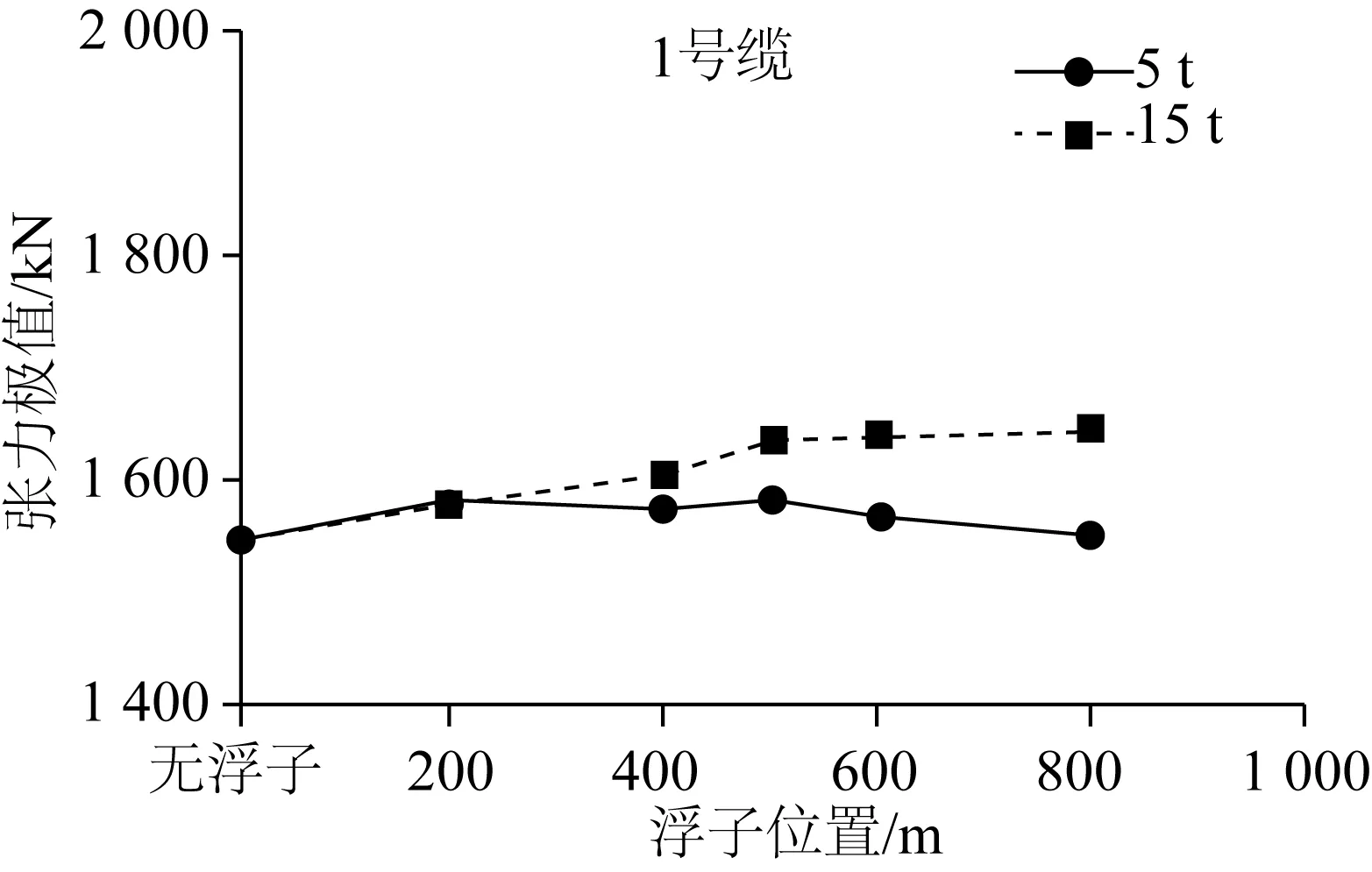
图7 1号缆张力极值随浮子位置变化情况Fig. 7 Maximum tension of Line 1# for different buoy locations

2.3 浮子净浮力影响规律

由图8可知，设置浮子后平台纵荡运动极值均有所减小。随着浮子净浮力值的增大，平台纵荡运动极值先减小后增大。浮子净浮力为10 t左右时，平台纵荡位移极值达到最小，距离顶端400 m和500 m缆长处对应的纵荡极值分别是无浮子系统的79.17%和79.09%。

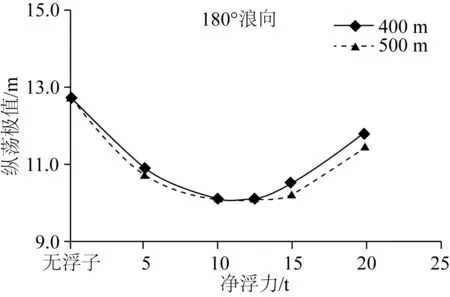
图8 纵荡运动极值随浮子净浮力变化曲线Fig. 8 Maximum surge of platform for different net buoyancies

由图9平台纵荡运动低频、波频有效值，随着浮子净浮力值的增大，平台纵荡低频有效值先减后增。当浮子净浮力为10 t时，平台纵荡低频有效值最小。

图9 浮子净浮力不同时平台纵荡波频、低频有效值Fig. 9 Wave and low frequency significant surge value of platform for different net buoyancy of buoy

由图10可知，受力最大的1号系泊缆张力随着浮子净浮力的增大先增后减，浮子净浮力为12.5 t时张力极值最大，导致安全系数略微降低，但仍满足系泊安全要求。

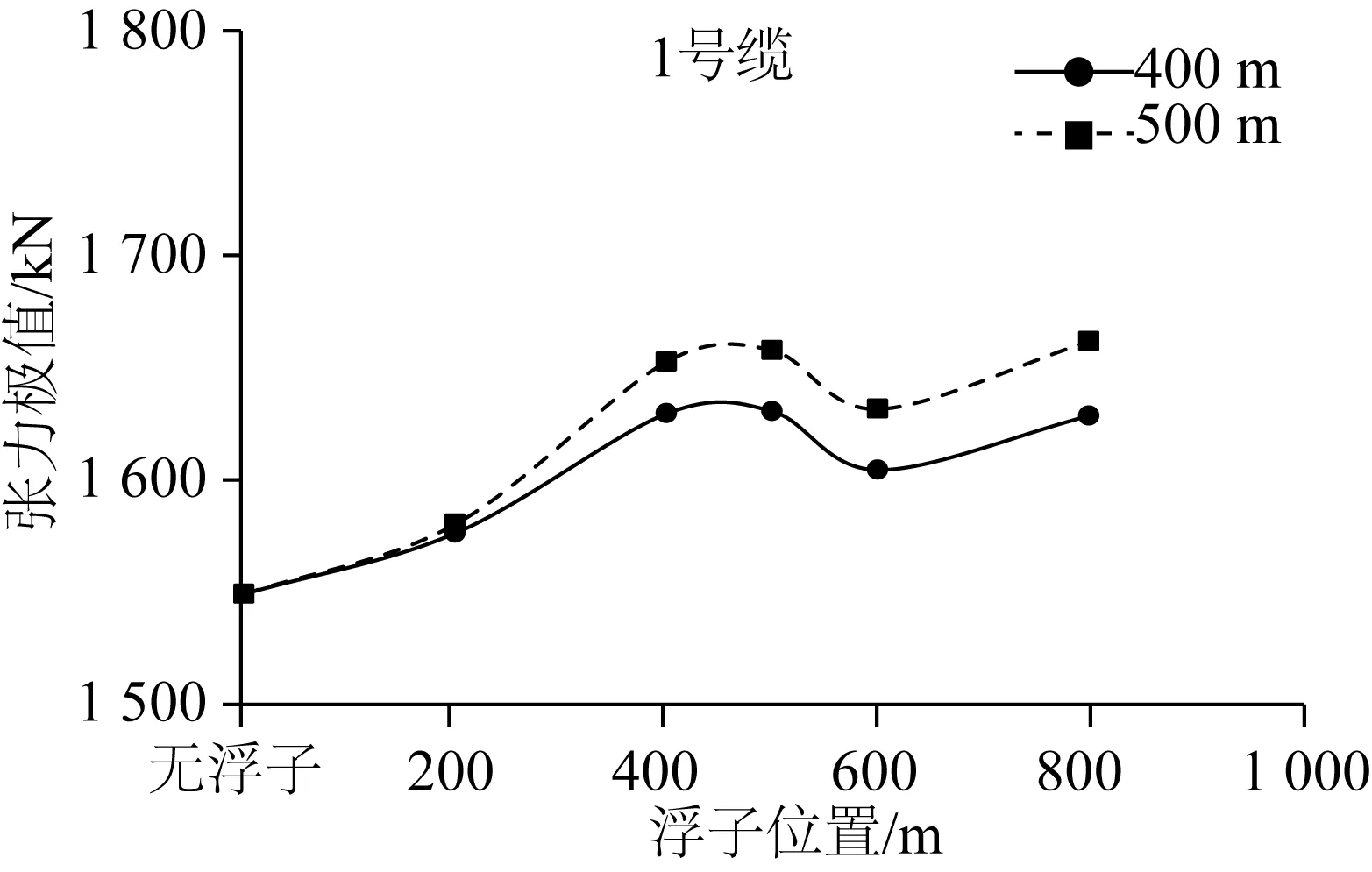
图10 1号缆张力极值Fig. 10 Maximum tension of Line 1# for different net buoyancy of buoy

图11 系泊系统纵荡回复力曲线Fig. 11 Restoring force curve of the mooring system in surge direction

因而，综合考虑平台位移及系泊缆张力情况，浮子净浮力取10 t，即0.4倍悬垂段缆长处，可以有效改善平台水平位移，同时满足系泊缆安全系数要求。

2.4 浮子式系泊系统优化方案

通过对浮子位置、净浮力大小进行系泊系统规律研究后，针对250 m半潜式平台浮子式系泊系统，选取优化方案为：浮子设置于距离系泊缆顶端一半缆长(500 m)的位置，提供净浮力为悬垂段缆重的0.4倍(10 t)。有无浮子两种系泊系统纵荡方向回复力曲线如图11所示，从静力角度，在维持系泊缆顶端预张力情况下，设置浮子可改变系泊缆张角形态而使得其能够为平台提供更大的回复力。下面采用耦合动力分析方法，综合考察不同浪向下(180°、135°和90°)平台运动性能和系泊缆受力特性，计算结果如表6和表7所示。

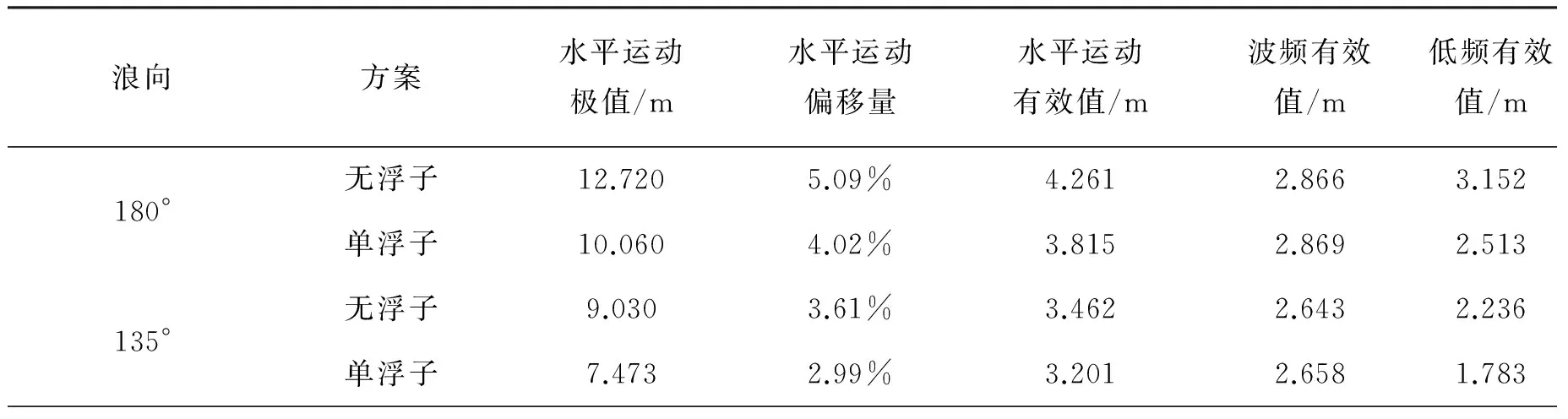
表6 平台水平运动结果(单幅)Tab. 6 Results of platform horizontal motion

(续表)

表7 平台系泊缆张力结果Tab. 7 Results of mooring line tension

由平台运动和系泊缆顶端张力计算结果可知：

1)浮子系泊系统方案对于降低平台水平面内运动的极值、有效值有较明显效果，而对这两者的降低作用主要是通过减小平台低频运动实现的。

2)受力最大系泊缆张力极值较无浮子状态有所增加，但仍有较充裕的安全裕量。系泊缆顶端张力标准差有所降低。

3 结 语

建立单浮子系泊系统的数值计算模型，验证浮子式系泊系统计算分析方法，详细分析浮子设计参数(设置位置和净浮力大小)变化对系泊缆张力特性与平台运动的影响规律，并根据得到的规律选择了优化的浮子系泊系统方案。最后对优化方案进行评估，表明优化方案可以显著降低了系泊中的平台水平运动，尤其是低频运动，同时系泊缆张力变化不大，仍满足安全要求。通过本研究可以总结出以下规律：

1) 在保证预张力不变的情况下，浮子系泊系统可以显著减小平台水平面内的运动，这种减小作用主要是通过改善低频下的平台运动实现的。

2) 单个浮子设置在距离靠近悬垂段缆长1/2处时对于改善平台纵荡运动效果最佳。此时系泊缆张力极值有所增加，但仍有较高的安全裕度，同时张力响应标准差也有所减小。

3) 浮子净浮力取值为悬垂段缆重0.4倍时，既可使得平台运动尤其是低频运动有较明显的改善，又可以保证系泊缆张力在较安全范围内，且张力响应程度有所减小。

4) 单浮子最佳方案为浮子设置在距离顶端1/2倍悬垂段缆长位置处，浮子提供0.4倍悬垂段缆重。与无浮子方案比较，单浮子方案能够明显减少顶浪下平台纵荡位移，且系泊缆张力在安全范围内。

[1] 王俊荣, 谢彬. 半潜式平台水动力性能及运动响应研究综述[J]. 中国造船, 2009,50(S):255-260. (WANG Junrong, XIE Bin. Review of hydrodynamic performance and global motion prediction of semi-submersibles[J].Shipbuilding of China, 2009, 50(S): 255-260.(in Chinese))

[2] MAVRAKOS S A, NEOS L, PAPAZOGLOU V J, et al. Systematic evaluation of the effect of submerged buoys’ size and location on deep water mooring dynamics[C]//Proceedings of the 4th Int, Symp. on Practical Design of Ships and Mobile Units. 1989,3(105): 1-105.

[3] MAVRAKOS S A, PAPAZOGLOU V J, TRIANTAFYLLOU M S, et al. Experimental and numerical study on the effect of buoys on deep water mooring dynamics[C]//Proceedings of the 1stInt, Offshore and Polar Engineering Conf.. 1991: 243-251.

[4] MAVRAKOS S A, CHATJIGEORGIOU J, PAPAZOGLOU V J. Use of buoys for dynamic tension reduction in deep water mooring applications[C]//Proceedings of the 7thInt. Conf. on the Behaviour of Offshore Structures, BOSS’94. 1994: 417-426.

[5] 王道能.浮筒锚泊系统受力分析及其仿真[D]. 哈尔滨:哈尔滨工程大学,2008. (WANG Daoneng. Analysis and simulation of mooring system with buoys[D]. Harbin:Harbin Engineering University, 2008. (in Chinese))

[6] MAVRAKOS S A, CHATJIGEORGIOU J. Dynamic behavior of deep water mooring lines with submerged buoys[J]. Computers and Structures,1997,64(1-4):819-835.

[7] CHEN Peng, MA Jun. Performance evaluations of taut-wire mooring system for deepwater semi-submersible platform[C]//Proceedings of the thirtieth Offshore Mechanics and Artic Engineering Conference. 2011: OMAE2011-49229.

[8] 闫功伟, 欧进萍. 基于AQWA的张力腿平台动力响应分析[J]．东南大学学报，2009, 39(S2)：304-310. (YAN Gongwei, OU Jinping. Dynamic response analysis of TLP based on AQWA[J]. Journal of Southeast University, Natural Science Edition, 2009, 39(S2)：304-310. (in Chinese))

[9] ANSYS. Inc software. AQWA-LINE manual[S]. 2011.

[10] ANSYS. Inc software. AQWA-DRIFT manual[S]. 2011.

[11] MAVRAKOS S A, PAPAZOGLOU V J, Triantafyllou. Deep water mooring dynamics[J]. Marine Structures, 1996: 181-209.

[12] KIM Youngbok. Dynamic analysis of multiple-body floating platforms coupled with mooring lines and risers[D]. Texas A & M University, 2003.

[13] API RP 2SK, Recommended practice for design and analysis of station keeping systems for floating structures[S]. Third Edition, American Petroleum Institute, 2005.

Study on the parameters optimization for the mooring system with buoys of a semi-submersible

WU Lan1, KUANG Xiaofeng1, FAN Yali1, WANG Fei2, LI Xinxin2

(1. National Key Laboratory of Science and Technology on Hydrodynamics, China Ship Scientific Research Centre , Wuxi 214082, China; 2. Dalian Shipbuilding Industry Co., LTD, Dalian 116000, China)

1005-9865(2016)04-0030-08

P751

A

10.16483/j.issn.1005-9865.2016.04.005

2015-06-01

国家发改委海洋工程装备研发及产业化专项

吴 澜(1988-)，女，天津人，硕士，主要从事海洋工程水动力学方向的研究。E-mail： wulan135@126.com