波浪要素对水平圆柱杆件水动力系数影响研究
2016-10-12姚晓杰桂福坤陈天华
姚晓杰,桂福坤,孟 昂,陈天华
(浙江海洋学院 国家海洋设施养殖工程技术研究中心,浙江 舟山 316000)
波浪要素对水平圆柱杆件水动力系数影响研究
姚晓杰,桂福坤,孟 昂,陈天华
(浙江海洋学院 国家海洋设施养殖工程技术研究中心,浙江 舟山 316000)
通过试验研究了波浪要素对水平固定圆柱杆件水动力系数的影响。试验利用垂直杠杆原理,提取了杆件在波浪下的水平受力历时曲线,基于改造的莫里森方程,计算了不同波浪要素下的水动力系数CD和CM取值。定义分析了新的波高参数KH,周期参数KT和雷诺数Re对水动力系数的影响。研究表明,整体拟合法与四点拟合法获得的水动力系数在数值上差异不大。KH、KT及Re均对水动力系数的取值有较显著影响:1)随着波高KH的增大,CD、CM整体呈幂指数衰减,且CM的衰减更为迅速;2)随着波周期KT的增大,CD、CM整体亦呈衰减趋势; 3)相同波高条件下,CM随Re数增大而增大,而CD值相对稳定。最后给出了波浪条件下水动力系数CD和CM的经验计算公式。
水动力系数;波浪要素;水平杆件结构物;雷诺数;莫里森方程;线性波理论
Abstract:The relationship between the horizontal fixed bar structures and the wave parameters was studied.And an upright lever was designed in the experiment to extract the horizontal wave force in time series.Based on the reformed Morison equation,the hydrodynamic coefficients ofCDandCMwere calculated.Wave height parameterKHand wave period parameterKTwere investigated and defined.The impact of wave elements includingKH,KTand Reynolds numberRewas analyzed on the hydrodynamic coefficient.The result shows that all the wave parameters,including wave height (KH),wave period (KT) and Reynolds number (Re),have significant influence on the values of hydro-coefficientsCDandCM.The results show:1) both hydro-coefficientsCDandCMdecrease as the wave heightKHincrease with a powered fitted function; 2)CDandCMalso decrease as the wave periodKTincreases.However,the fitted relationship is not uniform; 3) given the same wave height,CMincreases as Reynolds number (Re) increases.However,CDchanges little.Based on the results achieved,the authors also give an empirical formula for calculating hydro-coefficientsCDandCM,which may give guidance in practical use.
Keywords:hydro-coefficients; wave parameters; horizontal cylinder structure;Reynolds number; Morison equation; linear wave theory
小尺度的杆件结构物广泛应用于各种网箱、筏式、围网等养殖工程设施中[1-3],是海洋工程结构物的重要结构单元。对于小尺度杆件结构物,一般采用Morison方程计算其波浪力[4],而确定其中的拖曳力系数CD和惯性力系数CM是问题的关键所在。李玉成等[5]对垂直方柱在波浪作用下的受力做了试验研究,并对时域下CD和CM的5种算法做了较系统的探讨,在分析规则波浪时,认为选取线性波理论和最小二乘法所得的结果相对较好。邢至庄等[6]对接近海底的水平管做了分析,通过多种方法计算得到CD和CM,结果显示,使用二阶Stocks波浪理论并使用最小二乘加权平均值法更加符合试验结果。可见对不同位置、类型的模型,各个方法计算所得的水动力系数结果存有差异,应根据具体的情况选择相应的计算方法。研究表明,波浪要素对水动力系数取值有影响。在诸多研究中,KC数、Re数是最为常用的影响要素,如文献[7-10]等均认为KC数与水动力系数的变化相关性显著。然而,也有研究认为,对波动或者震荡流而言,用Re数与KC数的比值β作为影响水动力系数变化的因子更为合适[11]。KC数一直被认为是描述波浪的周期特性参数,而事实上,对KC数计算公式中各因子进行变换后发现,KC数实际上是与波高有关的参数。在诸多研究中,分析水动力系数取值时,一般假设水动力系数在整个波浪作用过程中保持不变,在实际应用中也能得到尚可接受的结果,而事实上水动力系数也是时间(或相角)的函数。李玉成等[4]即总结认为,水动力系数CD和CM是KC数、Re数和模型粗糙度以及时间的函数,并给出了水动力系数随相角的变化情况。
目前,关于波浪条件下的水动力系数研究,多数针对垂直桩柱或倾斜桩柱[7-8],而波浪水质点运动沿水深变化,波浪作用较为复杂,是水动力系数规律较为离散的原因之一。另一方面,多数研究关注波浪对杆件结构的综合作用,而水质点运动可离散为水平和垂直两个方向,综合作用下的水动力系数可以认为是两个方向独立作用的叠加,但由于二者存在π/2的相位差,事实上这种叠加往往使水动力系数的关系变得复杂。针对上述问题,以水平圆柱杆件结构物模型为研究对象,设计专用的测试装置,通过垂直杠杆原理,提取了固定水平圆柱杆件在波浪作用下的水平受力历时曲线,有效规避垂直受力的交叉影响。同时,分析探讨波高参数KH、波浪周期参数KT、雷诺数Re对杆件水动力系数的影响,为准确地计算波浪条件下小尺度杆状结构物的波浪力提供重要参考。
1 模型试验
1.1试验设备及布置
试验在研究中心水动力水槽中进行。水槽底面平坦,尺寸为130 m×6.1 m×3.5 m(长×宽×深),配置拖车和液压摇板式造波机,最大波高0.35 m,周期0.5~5 s,拖车最大拖速6.5 m/s。水槽另一端布置有消波装置,实验模型布置于水槽中离造波机距离约15 m处,此处波形最优。受力采用总力传感器测量,量程100 N。传感器在测量前均经过率定,线性置信度均在0.999以上。试验所用模型管为PVC材质,可认为是刚性结构。模型管长l统一设置为0.6 m,直径D分别为0.03 m、0.05 m、0.075 m。
波浪水质点运动可分解为水平和垂直运动,为了便于受力分析,设计了专用的垂直杠杆式受力采集装置,可有效规避垂直受力的交叉影响,提取水平单一方向的受力过程。该装置为全钢制结构,入水部分为流线型支架,具有较高的刚度,避免产生结构共振。采集装置整体架设于水槽拖车上,模型杆件采用PVC管,水平布置于装置底部,距离装置转动轴心L1=0.8 m。PVC管两侧采用橡胶塞进行固定,试验时杆件模型布置于水面以下z=-0.3 m处,此时,水平面可达到的最低位置与模型管中心距离均大于等于模型4倍半径,可认为模型的存在不对自由表面产生影响。总力传感器布置于装置的上端,距离装置转动轴心距离L2=0.4 m。试验时,将波高传感器固定于装置侧边L3=0.4 m,用于采集实际波浪要素,采集周期为0.01 s。模型布置如图1~图3所示。

图1 模型平面布置示意Fig.1 Sketch of the model configuration

图2 受力采集装置平面示意Fig.2 Plan view of the force sampling unit
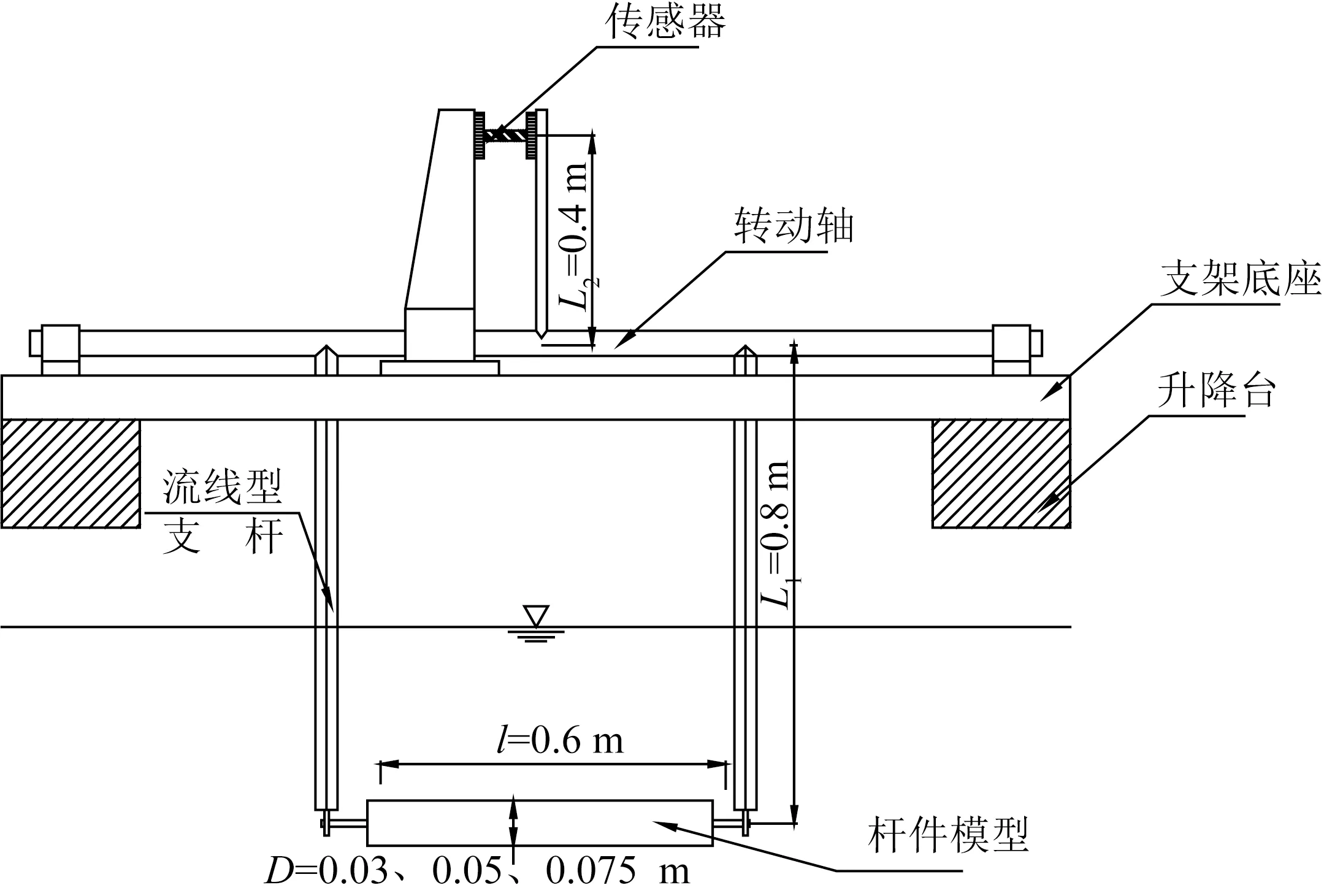
图3 受力采集装置立面示意Fig.3 Side view of the force sampling unit
1.2试验条件
波高和周期是波浪的两个基本要素。一般在研究波浪条件下水动力系数规律时,常取KC数、Re数等作为波浪设计要素。KC数常被认为是描述波浪周期的重要参数,具有以下形式:
根据深水线性波浪理论,可知:
代入KC数表达式中,有
上式表明,KC数实际上并非描述周期的参数,而是描述波高的参数。为便于后文讨论,重新定义新的参数KH,用于描述波高要素:
类似的,定义用于描述波浪周期的无量纲参数:
本试验将同时考察雷诺数Re对水动力系数的影响。分析可知,雷诺数Re实际上是描述波高、周期和杆件直径影响的综合因子。本试验波浪要素设计如表1所示。
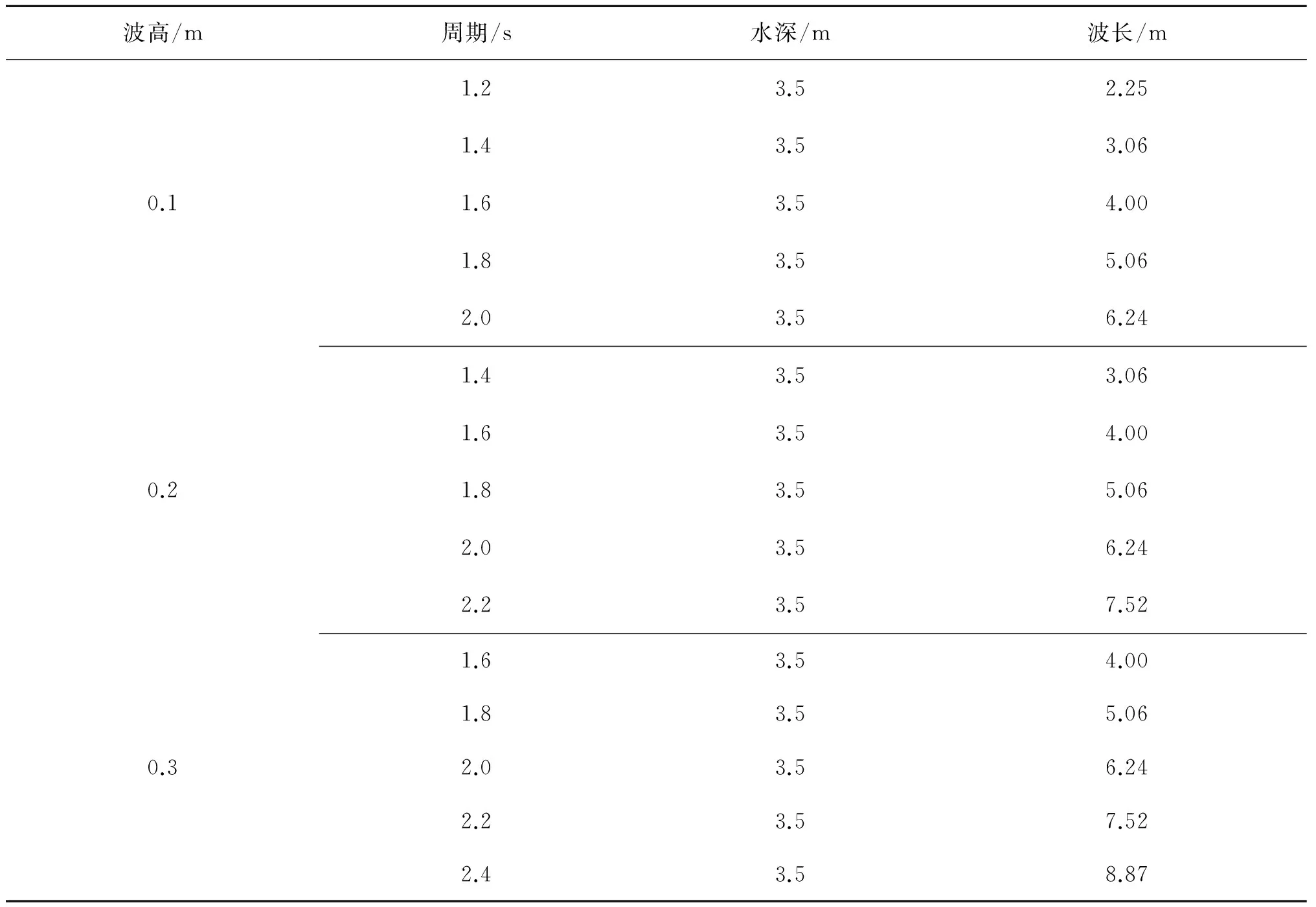
表1 试验波浪要素Tab.1 Wave parameters for the experimental tests
1.3数据处理
1)Morison方程的改造
Morison方程是1950年由莫里森等人提出来的。当结构特征直径D与波长L相比很小(D/L≤0.15)时,波浪场受结构的影响可以忽略,在本试验条件下,采用线性波浪理论,可用下式计算:
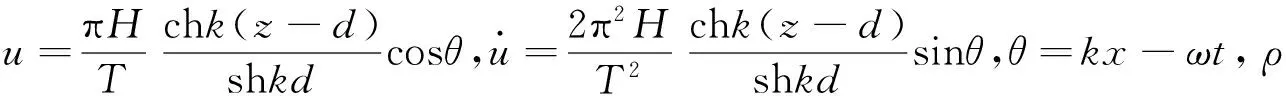
Morison公式由拖曳力和惯性力两部分组成,两者存在相位差。叠加以后的曲线一般会出现双峰或坎坡现象,本试验实测受力曲线总体较为平滑,无显著的双峰或坎坡现象,如图4所示。为更好地实现数据拟合,对Morison公式进行改造:将式(6)中拖曳力的|u|改为|umax|,其中|umax|为圆柱中心(z=-0.3 m)处波浪水质点最大速度,具体如下:
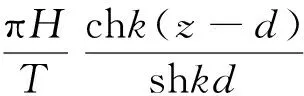
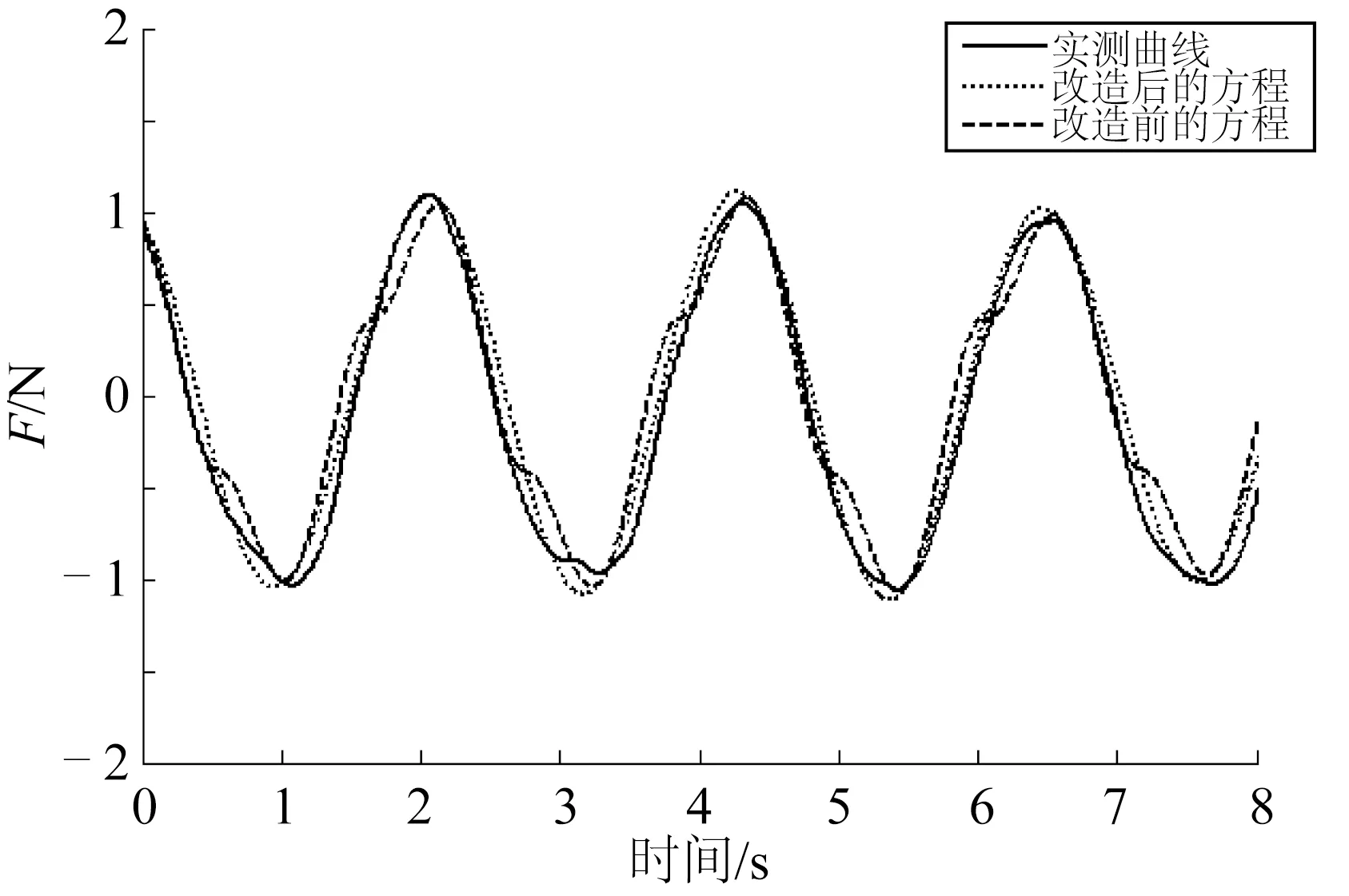
图4 Morison方程改造前后受力曲线与实测结果的比较Fig.4 Comparison of force curves before and after reformation of Morison equation (H=20 cm,T=2.2 s,D=5.0 cm)
2)数据处理方法
采用整体拟合法和四点拟合法对水动力系数进行分析。整体拟合法是指用最小二乘法对数据进行多元回归,拟合得到Morison方程的系数CD和CM。四点拟合法是指选取波浪波峰点、波谷点、上跨零点和下跨零点对应的数据进行分析。波浪处于波峰点和波谷点时,水平加速度为零,Morison公式中的惯性力为零,可直接求出拖曳力系数CD;波浪处于上跨零点和下跨零点时,水平速度为零,Morison公式中的速度力为零,可直接求出惯性力系数CM。整体拟合法假设整个波浪过程中水动力系数保持不变,而四点拟合法可获得对应点的水动力系数确定数值。
本试验条件下对应最大相对波高H/d=0.086<<0.2,相对水深d/L=0.39>0.2,因此非线性可以忽略[4,12],波浪要素计算时可采用线性波理论。在同一波要素下,实际产生的波浪波高和周期不可能完全一致,为避免该差异,具体分析时,将实际采集到的波浪根据上跨零点拆分为单个波浪来逐一分析,得到每个波浪的波高和周期值,采用线性波浪理论计算对应的速度和加速度。拟合分析后,将得到的水动力系数CD和CM进行平均。
2 结果与分析
2.1数据处理方法对水动力系数拟合结果的影响
采用整体拟合法和四点拟合法对不同波浪条件下的水动力系数进行了拟合分析。图5给出了杆件直径0.05 m时,不同波浪条件下两种方法拟合得到的水动力系数。由图可见,两种方法分析得到的水动力系数差异不大,这在一定程度上说明,水动力系数在整个过程中整体变化不大,或者以最大分项受力点分析得到的水动力系数,代表整个波浪作用过程中的水动力系数取值是可以接受的。基于以上分析,将以四点拟合法得到的水动力系数结果作为分析波要素影响的依据。
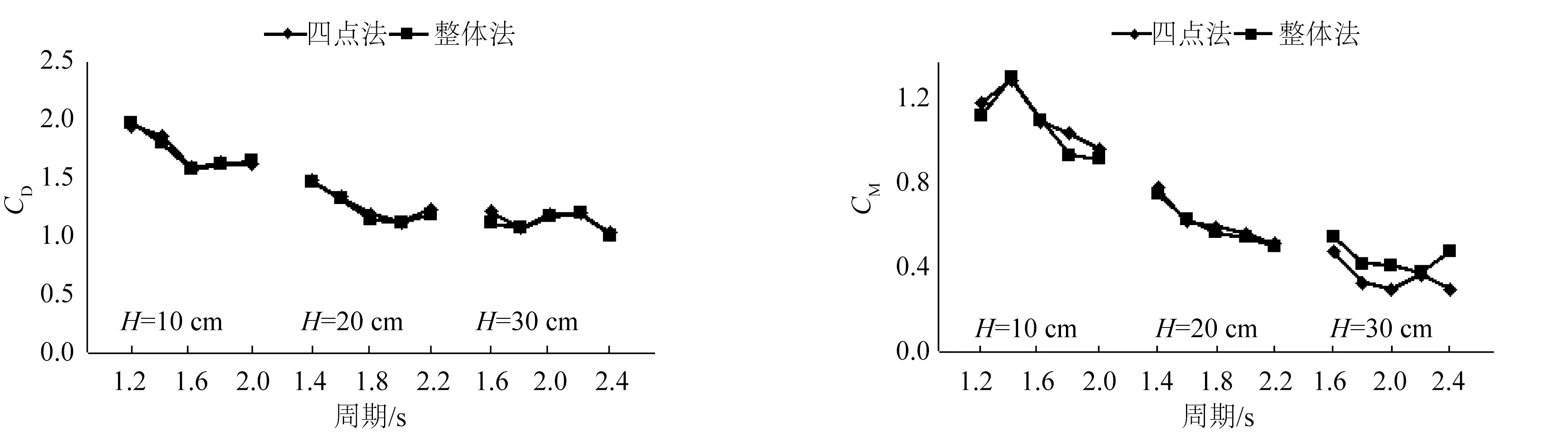
图5 四点法和整体法拟合结果比较Fig.5 Comparison of fitting results between Four-Point and Global approaches
2.2波浪周期KT对水动力系数的影响
图6和图7分别为波浪周期参数KT与水动力系数CD和CM的关系图。由图可见,KT对CD和CM均有影响,并且对CM的影响更加显著。CD在KT增加时,整体上略有减小的趋势,并随着KT的继续增加而趋于稳定。图6中明显还可以看到,CD除了与KT有关,还与波高有一定的关系,后文进一步分析。由图7可见,CM随着KT的增加都呈现良好的幂函数递减趋势。
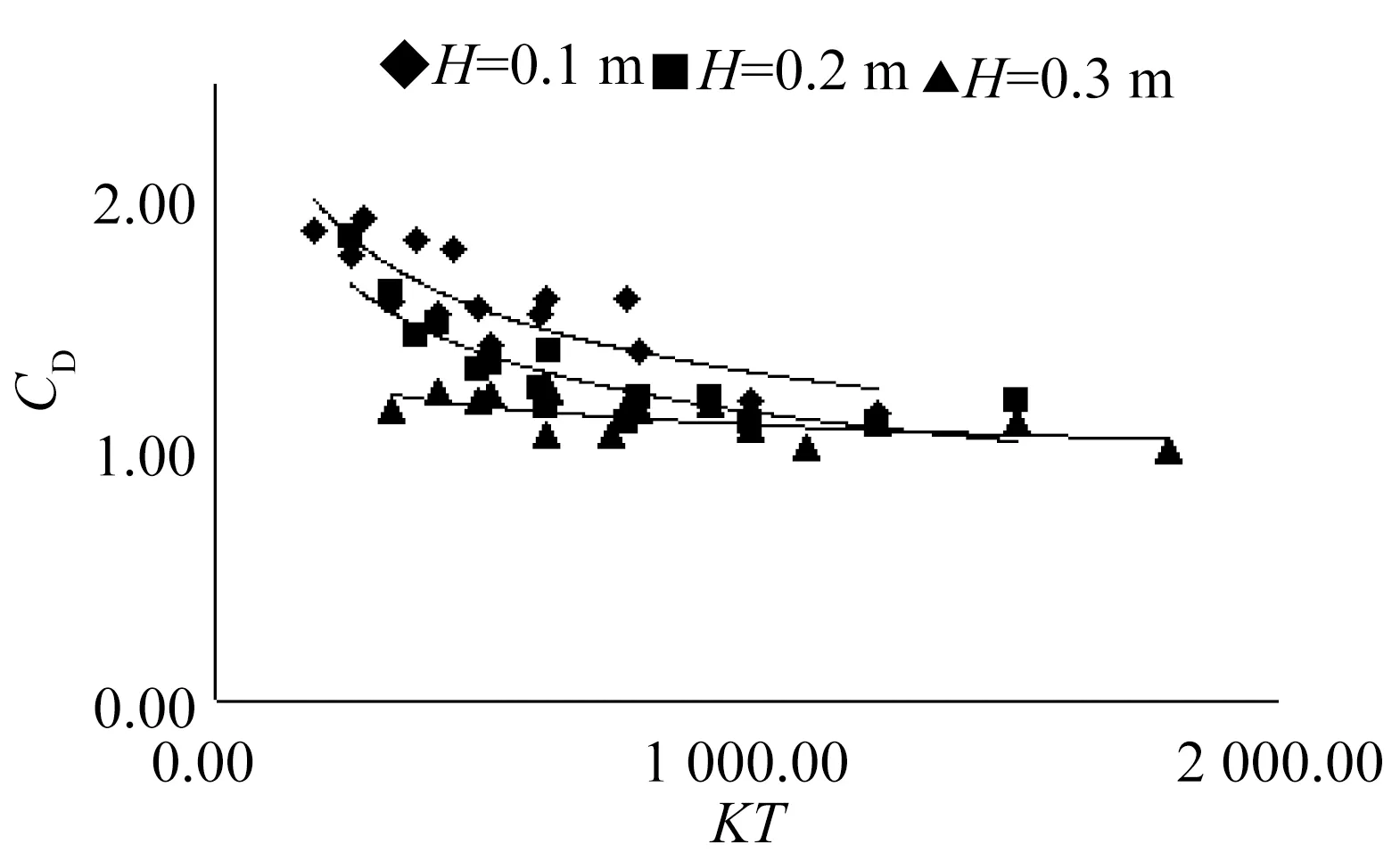
图6 波浪周期KT与CD的关系Fig.6 Relationship between KT and CD
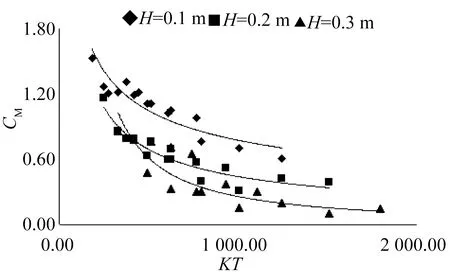
图7 波浪周期KT与CM的关系Fig.7 Relationship between KT and CM
2.3波高KH对水动力系数的影响
图8和图9分别为波高参数KH与水动力系数CD和CM的关系图。由图可见,KH对CD和CM存在较显著影响。随着KH增加,CD值有减小趋势,并趋于稳定。KH对CM的影响是更为明显,从总体趋势看,随着KH增加,CM有显著的减小,与CD一样,随着KH的增加,CM也渐渐趋于平缓。此时的CM值已然很小,且大部分的CM值小于1.0,可见此时附加水质量系数为负数。据文献[12]研究,在KH大于10之后,其KC值在10至20之间,此时CM有一个明显的下降,且在雷诺数较小而KC数较大时,CM将小于1,这与本试验的结果相一致。
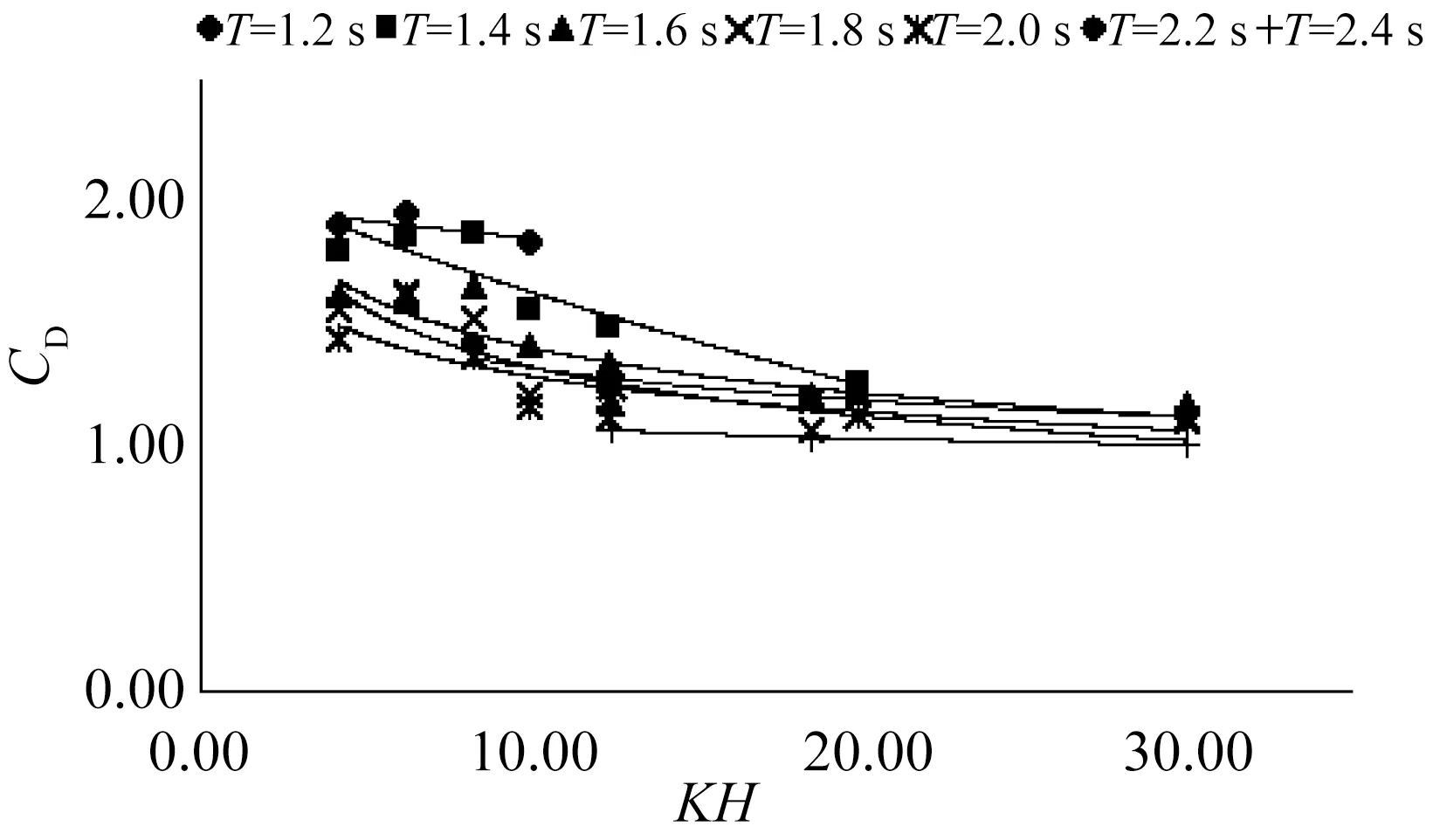
图8 波高参数KH与CD的关系Fig.8 Relationship between KH and CD

图9 波高参数KH与CM的关系Fig.9 Relationship between KH and CM
2.4雷诺数Re对水动力系数的影响
雷诺数定义为波浪水质点速度极大值和直径之积与运动黏滞系数之比:
如前文所述,雷诺数体现了波高、周期和杆件直径的综合因素,图10和图11分别为雷诺数Re与水动力系数CD和CM的关系图。尽管数值上两者关系较为复杂,但总体上CD和CM都随着Re的增大而呈增大趋势,即波高、周期和杆件直径对杆件受力存在交互效应。由图10可见,Re数对CD的影响相对较小,而对CM的影响较为显著。同时对比图10、图11可见,在不同波高下的CD和CM数值上存在差异,显然这是由于波高参数的影响引起的,前文已经做了相关探讨。
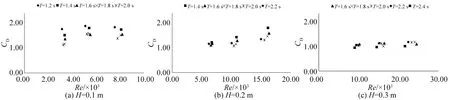
图10 CD与Re的关系图Fig.10 Relationship between Re and CD
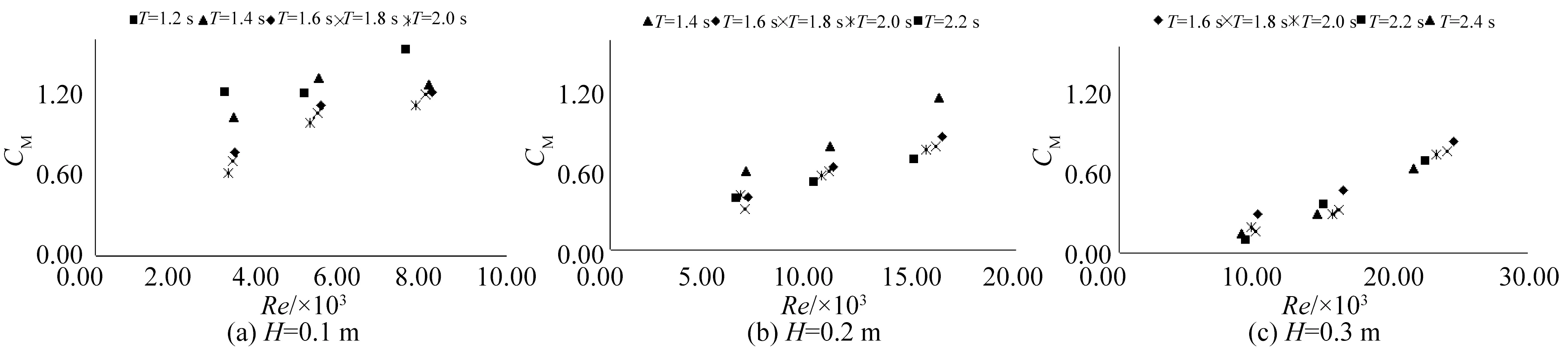
图11 CM与Re的关系图Fig.11 Relationship between Re and CM
2.5各因子对水动力系数的综合影响
综合前文所述,水动力系数与波高参数KH、周期参数KT和雷诺数Re均存在相互关系。这里认为KH、KT和Re是影响水动力系数变化的三个重要影响因子,采用多元拟合方法可得到水平杆件的水动力系数与上述三个重要因子的经验关系式:


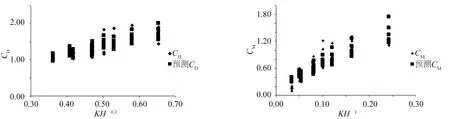
图12 试验值和预测值比较Fig.12 Comparison of experimental and predicted values
上述拟合公式计算所得受力的相对误差均值为8.4%,如图12所示CD和CM试验值与预测值比较吻合。上述公式表明,常数项可认为是两个水动力系数的特性值,即对于速度力系数CD,其特征取值为1.73;对惯性力系数CM,其特征取值为1.26。各影响因子KH、KT、Re可理解为波浪和杆件参数对水动力系数特征取值的附加影响,而波浪参数的系数和幂的取值则表示了各个波浪参数对波动贡献的大小和规律变化。
3 结 语
研究了不同直径的水平杆件(光滑PVC浮管)在波浪作用下的受力特性,采用整体拟合和四点拟合法分析了杆件在波浪作用下的水动力系数。讨论了波高参数KH、周期参数KT、雷诺数Re对水动力系数的影响,取得以下基本结论:
1)在水平杆件的波浪力分析时,将Morison方程的速度力项中的水质点速度|u|改为|umax|,有助于提高数据拟合分析的精度。
2)在波浪影响分析中常用的波浪特性参数KC数,其本质是描述波高特征的无量纲化参数,并非描述波浪周期的特性参数。
3)周期参数KT对水动力系数有显著的影响,水动力系数CD和CM均随着KT的增大而减小,并随着KT继续增大而趋于稳定。
4)波高参数KH对水动力系数亦有较大影响,随着KH的增大,CD有减小的趋势并趋于稳定。KH对CM有非常显著的影响,随着KH的增大而以幂函数规律迅速减小。
5)雷诺数Re反映了波高、周期、杆件特征长度的综合影响,亦对水动力系数存在一定影响,而且对CM的影响更为显著。
6)采用多元拟合方法获得的水动力系数经验公式,可用于圆柱形杆件波浪力计算时的水动力系数值,但需注意其适用范围应不显著的超过本研究的范围。
关于水动力系数拟合分析时,采用整体拟合法和四点拟合法获得的结果较为接近,虽然可以近似的假设水动力系数在整个过程中整体变化不大,或者以最大分项受力点(波峰波谷点为最大水平速度力,上下跨零点为最大水平惯性力)分析得到的水动力系数,代表整个波浪作用过程中的水动力系数取值是可以接受的,但水动力系数在整个波浪过程中的真实情况可能是变化的,而且可能也是比较复杂的,需要进一步深入研究。
[1] DíAZ C,FIGUEROA Y,SOBENES C.Effect of different longline farming designs over the growth of Mytilus chilensis (Hupé,1854) at Llico Bay,VIII Región of Bio-Bio,Chile[J].Aquacultural Engineering,2011, 45 (3) :137-145.
[2] 张立斌.几种典型海域生境增养殖设施研制与应用[D].青岛: 中国科学院海洋研究所,2010.(ZHANG Libin.Development and application of several new system for culture and stock enhancement in typical habitats of sea areas[D].Qingdao:Chinese Academy of Sciences,2010.(in Chinese))
[3] 桂福坤,王炜霞,张怀慧.网箱工程发展现状及展望[J].大连水产学院学报, 2002,17(1):70-78.(GUI Fukun,WANG Weixia,ZHANG Huaihun.The development and prospect of sea cage engineering[J].Journal of Dalian Fisheries University,2002,17(1):70-78.(in Chinese))
[4] 李玉成,腾斌.波浪对海上建筑物的影响[M].第二版.北京:海洋出版社,2002.(LI Yucheng,TENG Bin.Wave action a maritime structures[M].2nd Edition.Beijin:China Ocean Press,2002.(in Chinese))
[5] 李玉成,王凤龙,何明.方柱水动力系数确定方法的探讨[J].海洋通报,1994,12(2):62-79.(LI Yucheng,WANG Fenglong,HE Ming.Method for determination of hydrodynamic coefficients for square cylinder[J].Marine Science Bulletin,1994,12(2):62-79.(in Chinese))
[6] 邢至庄,孙绍述,胡玉霞.接近海底水平管的波浪力和CD,CM,CL值的实验研究[J].海洋工程,1990,8(3):24-31.(XING Zhizhuang,SUN Shaosu,HU Yuxia.Study of wave forces andCD,CM,CLon horizontal cylinder near the ocean bottom[J].The Ocean Engineering,1990,8(3):24-31.(in Chinese))
[7] 李玉成,张福然.作用于垂直桩柱上的波浪水流力[J].海洋学报,1986,8(6):751-761.(LI Yucheng,ZHANG Furan.Wave and current force acting on the vertical cylinder[J].Journal of Oceanography,1986,8(6):751-761.(in Chinese))
[8] 李玉成,康海贵,费勤浩.规则波作用下倾斜桩柱的受力研究[J].水动力学研究与进展:A辑,1992,7(1):85-100.(LI Yucheng,KANG Haigui,FEI Qinhao.Wave forces on inclined cylinder in regular waves[J].Journal of Hydrodynamics,1992,7(1):85-100.(in Chinese))
[9] 徐梅坤,李玉成.作用于水平桩柱上的波流力[J].海洋学报,1988,10(1):107-116.(XU Meikun,LI Yucheng.Wave and current force acting on the horizontal cylinder[J].Journal of Oceanography,1988,10(1):107-116.(in Chinese))
[10] 康海贵.不同雷诺数下水平桩柱的水动力待征[J].水动力学研究与进展:A辑,1994,9(4):388-394.(KANG Haigui.Hydrodynamic force on smooth horizontal cylinder in uniform oscillatory flow[J].Journal of Hydrodynamics,1994,9(4):388-394.(in Chinese))
[11] SARPKAYA T,ISAACSON M.Mechanics of wave forces on offshore structures[M].California:Van Nostrand Reinhold Company,1981.
[12] 竺艳蓉.海洋工程波浪力学[M].第一版.天津:天津大学出版社,1991:59-62.(ZHU Yanrong.Wave mechanics for ocean engineering[M].1st Edition.Tianjin:Tianjin University Press,1991:59-62.(in Chinese))
Experimental study on hydro-coefficients of horizontal cylinder structure in waves
YAO Xiaojie,GUI Fukun,MENG Ang,CHEN Tianhua
(National Engineering Research Center for Marine Aquaculture,Zhejiang Ocean University,Zhoushan 316000,China)
TV139.2
A
10.16483/j.issn.1005-9865.2016.01.011
1005-9865(2016)01-0080-08
2014-10-16
国家自然科学基金(51109187,51239002);浙江省教育厅攀登计划(pd2013217);舟山市海洋专项(2013C41002)
姚晓杰(1989-),浙江杭州人,硕士,主要从事海洋养殖工程技术研究。E-mail:710181791@qq.com
桂福坤。E-mail:gui2237@163.com
