双定子超环面电机磁路模型与气隙磁场研究

刘欣，许立忠，聂岭

(1.天津工业大学 天津市现代机电装备技术重点实验室,天津 300387；2.燕山大学 机械工程学院,河北 秦皇岛 066004)



双定子超环面电机磁路模型与气隙磁场研究

刘欣1，许立忠2，聂岭1

(1.天津工业大学 天津市现代机电装备技术重点实验室,天津 300387；2.燕山大学 机械工程学院,河北 秦皇岛 066004)

双定子超环面电机是一种新型结构的空间电机，将动力和减速机构有机结合，在机器人和航空航天领域具有很好的应用前景。在对该电机的结构特点及运行原理进行分析的基础上，将其三维磁路分解为周向和环向磁路，并建立了简化的等效磁路模型。根据该电机的结构特点对磁路模型中各磁阻进行推导，并对其静态磁场的气隙磁密进行了解析求解。为了验证该磁路模型的准确性，运用有限元方法对其三维磁场进行仿真分析，并对研制实验样机的反电动势进行了测试实验。通过与仿真结果和实验结果进行对比分析表明，该等效磁路模型和参数计算方法是可行的，为进一步定量分析该电机的电磁性能提供了理论依据。

双定子；超环面电机；磁路模型；气隙磁密；有限元法

0　引　言

双定子超环面电机是在行星蜗杆集成传动的基础上[1-2]引入电磁的元素发展而来的一种新型空间电机，把电力和传动机械有机结合起来。由于集成传动本身具有减速功能，超环面电机就将动力和减速机构融为一体，继承了集成传动结构运行平稳和减速比大的优点，并且充分发挥了机电能量转换在电机中的作用。可见，它是将电磁驱动与减速环节有机结合，因此可以在很小的空间内传递较大的转矩，具有功率密度高和力能指标高的优势，该种电机除了航空、军事和车辆等要求结构紧凑的领域外，还在机器人和飞行器制导等控制要求较高的技术领域有着广阔的应用前景[3]。

超环面电机的结构是作者在研究行星蜗杆集成传动的基础上，借鉴电磁谐波传动[4]提出的，并且在超环面电机的结构分析、运动学和原理模型等方面进行了许多研究工作[5-8]。为了提高超环面结构中机电耦合系统的动态行为，文献[9-11]建立了该电机的振动模态分析模型，对其在外加激励作用下的强迫振动模态和包含内共振的非线性振动进行了研究。文献[12]根据毕奥萨伐尔定律建立了其蜗杆内定子电磁场的计算模型，对其磁场分布进行了仿真计算。超环面电机的结构新颖，目前对其电磁驱动机理的研究尚不成熟。由于该新型电机的爪式转子是在蜗杆内定子和环面外定子的共同作用下实现能量转换的，该电机的空间磁场就具有其特殊性。针对超环面电机双定子的环面结构特点，本文对其三维特性的磁通进行分解，建立该新型空间电机的磁路模型，并在推导各磁路磁阻解析公式的基础上对气隙磁密进行解析计算，通过有限元磁场仿真结果和样机测试实验对该磁路模型的正确性进行验证，为该新型电机的电磁参数优化设计和特性研究奠定理论基础。

1　电机结构及运行原理

双定子超环面电机的结构原理如图1所示，它主要是由蜗杆内定子、环面外定子和爪式转子组成。其内定子是由硅钢片叠压而成的蜗杆铁心、电枢绕组和中心轴构成，电枢绕组嵌放在蜗杆铁心环面的螺旋槽内以形成螺旋磁场；环面外定子是由永磁体或磁钢制成的空间螺旋梁组成，磁性螺旋梁均匀地嵌在环面外定子支架上；爪式转子固联一定个数的行星轮，行星轮圆周上嵌有NS极相间的永磁齿，每个行星轮轴与转子输出轴垂直，行星轮磁齿在内外定子磁场的作用下做环状的螺旋运动，使得行星轮在自转的同时公转，由于爪式转子与行星轮中心轴的固联，行星轮的公转会带动爪式转子转动，从而实现运动和动力的输出。爪式转子的输出转速符合行星传动的减速关系，所以其与内定子旋转磁场的同步转速之间有一定的减速比，可见，该双定子超环面电机综合了行星蜗杆传动的大传动比与永磁同步电机无接触电磁啮合的优点，实现了机电磁有机结合的直接驱动。

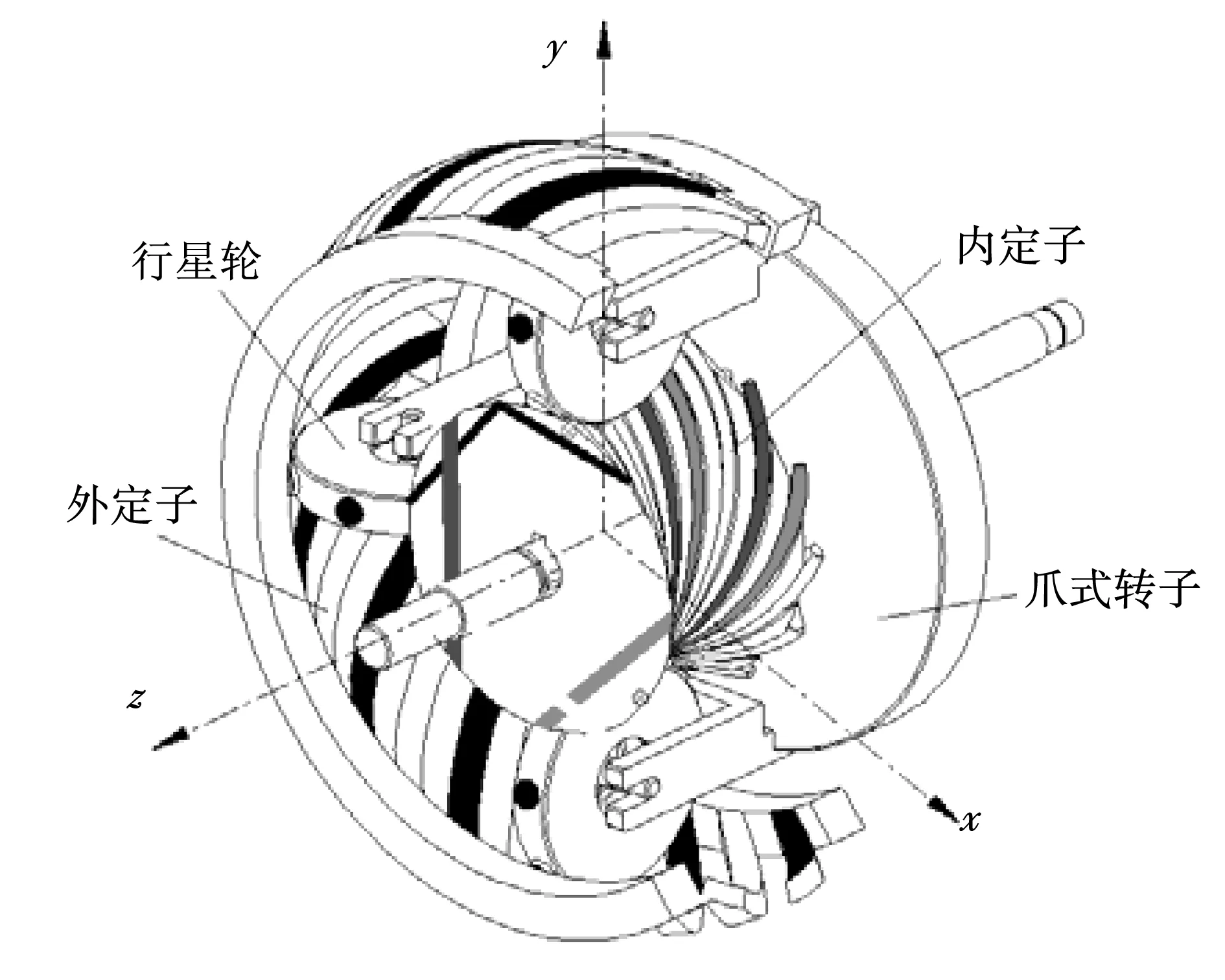
图1　超环面电机结构原理图Fig.1　Schematic structure of toroidal motor

由图1可以看出，由超环面电机两个定子产生的磁场均为空间螺旋结构，它们与行星轮磁齿之间形成的空间磁路就具有三维特性，但三者之间又满足严格的电磁啮合关系，故该电机磁路具有其规律性。在对超环面电机这一特定本体结构分析的基础上，采用场化路的方法，将三维磁路进行周向和环向分解，把实际存在的不均布的磁场转化成等效的分段磁路，并假定每段磁路磁通沿截面均匀分布。这种把磁场计算转化为磁路计算的方法不仅会减小计算量，同时也对分析双定子超环面电机的参数设计规律和性能优化具有重要意义[13-16]。为了提高等效磁路解析方法的计算精度，结合计算精度高的有限元方法对其三维磁场分布进行仿真，从而来修正该电机等效磁路模型中的系数，使得磁路法在明确反映气隙磁场特性与电机结构参数解析关系的基础上更具有工程实用性。

2　等效磁路模型

2.1磁路模型建立

研究的双定子超环面电机整体磁路分为两部分，包括蜗杆内定子与行星轮磁齿在电机内侧形成的磁路和外定子与行星轮磁齿在电机外侧形成的磁路。蜗杆内定子电枢绕组通电后产生的合成磁场和外定子永磁齿形成的永磁场通过气隙均与行星轮磁齿构成闭合磁路，由于该电机内定子环面上的电枢绕组和外定子的永磁梁都是空间螺旋的，因此它们与行星轮磁齿之间形成的磁路就具有了空间特性。为了便于进行定量的分析和计算，现把电机内侧和外侧的空间的磁路都分解为如图2磁通示意图所示的周向和环向磁路，其中图2(a)所示磁路在蜗杆内定子截圆的圆周方向上，为磁路的周向分量；图2(b)所示磁路在蜗杆内定子外环面的截面内，为磁路的环向分量。由此将三维气隙磁场问题简化为两个二维磁场问题，在保证满足工程计算精度的前提下，简化了磁路解析模型。

图2　超环面电机磁通示意图Fig.2　Diagram of magnetic flux of toroidal motor

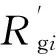
图3中F0、F1和F2分别为环面外定子、行星轮磁齿和蜗杆内定子电枢绕组提供的励磁磁动势；磁路模型的上半部分为外侧磁路，其中Φm0为外侧磁路的主磁通，Φm1为外侧磁路周向磁支路的磁通，Φ1为外侧不存在分量间耦合的周向独立磁通，Φm2为外侧磁路环向磁支路的磁通；磁路模型的下半部分为内侧磁路，Φn0为内侧磁路的主磁通，Φn1为内侧磁路周向磁支路的磁通，Φn2为内侧磁路环向磁支路的磁通，Φ2和Φ3为不存在分量间耦合的环向独立磁通。外侧和内侧磁路由爪式转子上的行星轮连接成一个整体磁路，其中包含耦合磁路和独立磁路。

图3　超环面电机的等效磁路模型Fig.3　Equivalent magnetic circuit model for the toroidal motor

2.2模型参数计算

在对双定子超环面电机磁通分布进行分析的基础上，计算各段磁路上由磁导系数和电机结构参数决定的磁阻，对于其中不规则的磁通路径需要忽略小量并简化为可以计算的形状。磁齿内阻和导磁材料的磁阻相对气隙磁阻对整个电机磁路和气隙磁场影响较小，可以将其忽略[17-19]。若蜗杆内定子与行星轮磁齿间气隙为δ1，则内侧磁路气隙磁阻

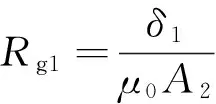
(1)

式中A2为行星轮磁齿截面积。同理可得

(2)

式中：r1为蜗杆截圆半径；h2为行星轮磁齿高；k为行星轮个数。行星轮材质为铝，则其齿间轭部磁路磁阻

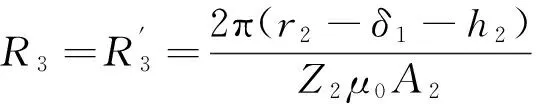
(3)

式中：r2为蜗杆环面半径；Z2为行星轮磁齿数。

若外定子与行星轮磁齿间气隙为δ0，可得外侧磁路环向气隙磁阻

(4)

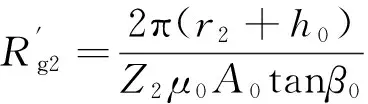
(5)

式中：h0为外定子磁齿厚度；A0为外定子磁齿的周向截面积；β0为外定子磁齿的螺旋升角[20]。当行星轮磁齿与外定子磁齿间完全啮合时，有

(6)

外侧磁路的周向气隙磁阻

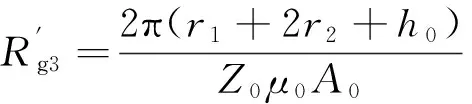
(7)

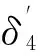
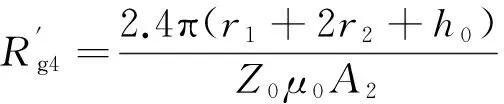
(8)

行星轮磁齿与内外定子之间耦合磁路的磁通，可由图3所示超环面电机的等效磁路模型和分量磁回路之间的耦合关系得到磁路方程：

(9a)

(9b)

式中：Rm1和Rm2分别为外侧磁路周向和环向磁支路的总磁阻；Rn1和Rn2分别为内侧磁路周向和环向磁支路的总磁阻。

根据超环面电机等效磁路中的磁阻计算值，由磁路方程可以得到

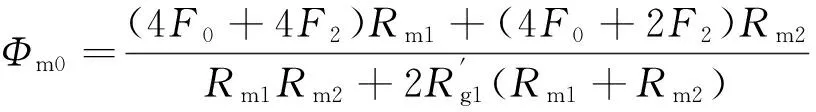
(10a)

(10b)

2.3气隙磁密

要得到整个气隙磁通密度的分布情况，还需对周向和环向分量磁路中独有的磁路进行求解，如图2中的Φ1、Φ2和Φ3，由于它们之间不存在耦合，可以直接求出。在忽略磁通路径中小量的同时引入磁通路径系数，由磁路中的欧姆定律可得

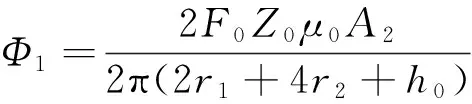
(11)

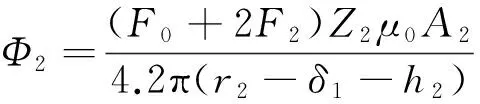
(12)

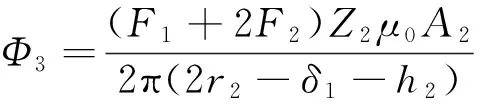
(13)

由于超环面电机爪式转子上行星轮磁齿与内外定子间的气隙磁场是该新型电机产生磁场力的关键，在对内外定子螺旋磁场与行星轮磁齿之间分量磁路进行分析的基础上可知周向磁路磁阻相对较大，且仅包含产生磁场力作用的耦合磁路的周向分量因素，而环向磁路中除了包含所有参与电磁啮合的磁齿和磁极，还包含行星轮磁齿与内外定子间气隙磁通密度的分布情况。所以采用对磁路模型中的环向分量进行解析计算，再计入周向分量的方法求得气隙磁密分布更具有工程应用价值。

考虑耦合磁路中的周向分量，在环向磁路分量解析计算结果中引入修正系数即可得到超环面电机静态磁场气隙磁密分布情况。把空间三维磁路分解得到的环向和周向磁密进行叠加时，由内外定子螺旋磁场的电磁啮合关系，得到其耦合修正系数

(14)

式中i取0，1时，可以分别得到外定子和内定子与行星轮磁齿间耦合磁路系数。

3　静磁场仿真分析

静态磁场的有限元仿真分析对研究双定子超环面电机至关重要，由于该电机漏磁路较多，其等效磁路模型忽略了其中部分因素，该方法可以比较准确地得到超环面电机气隙磁通密度的分布，对该电机的电磁设计有一定的参考价值。

3.1磁场仿真

为了验证气隙磁通密度解析解法的合理性，运用Ansoft有限元软件对超环面电机的气隙磁密进行仿真分析。表1给出了该电机的主要结构参数。图4为双定子超环面电机三维有限元模型的网格剖分图。

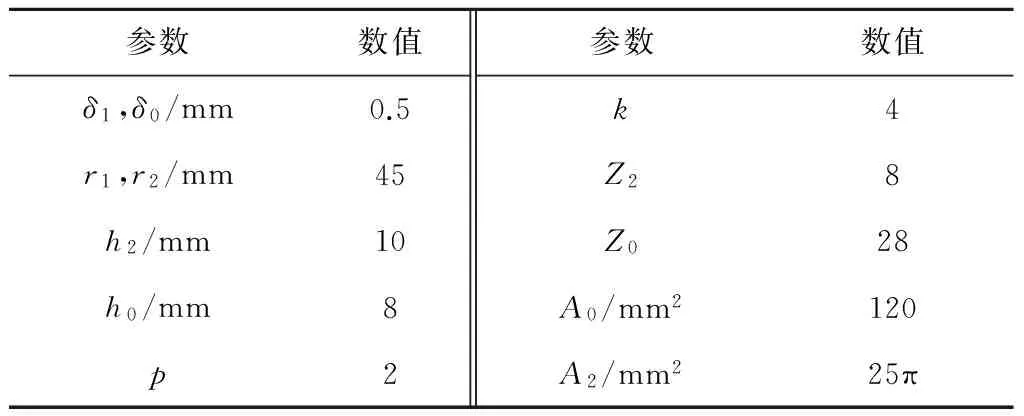
表1　电机主要结构参数

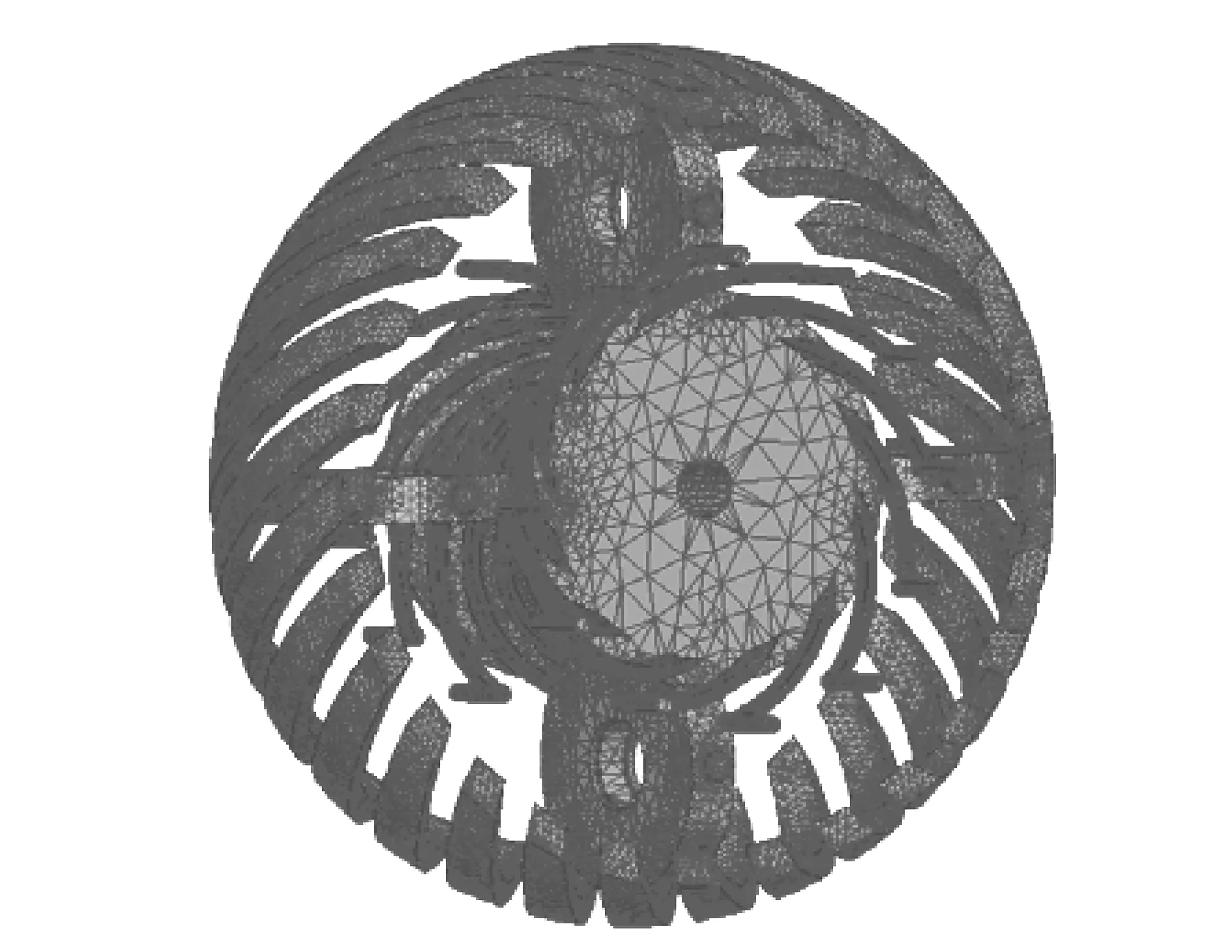
图4　超环面电机三维有限元剖分图Fig.4　3D FEM subdivision for the motor

对建立的超环面电机有限元模型进行求解，得到该电机磁通密度云图的分布情况如图5所示。由图5可以看出静态气隙磁场在行星轮磁齿与内外定子的电磁啮合处分布较集中，其余空间的磁密很小，几乎为零。

3.2气隙磁密分布

为了将三维磁场仿真结果和由磁路模型求得的磁密解析解进行对比分析，在三维模型中指定爪式转子上某一行星轮与内外定子间的气隙圆周路径。由静态磁场计算器求得该路径上的磁密仿真结果，并将此仿真结果和考虑磁路耦合加入修正系数的模型解析结果进行对比如图6所示。

图5　磁通密度云图Fig.5　Nephogram of magnetic flux density

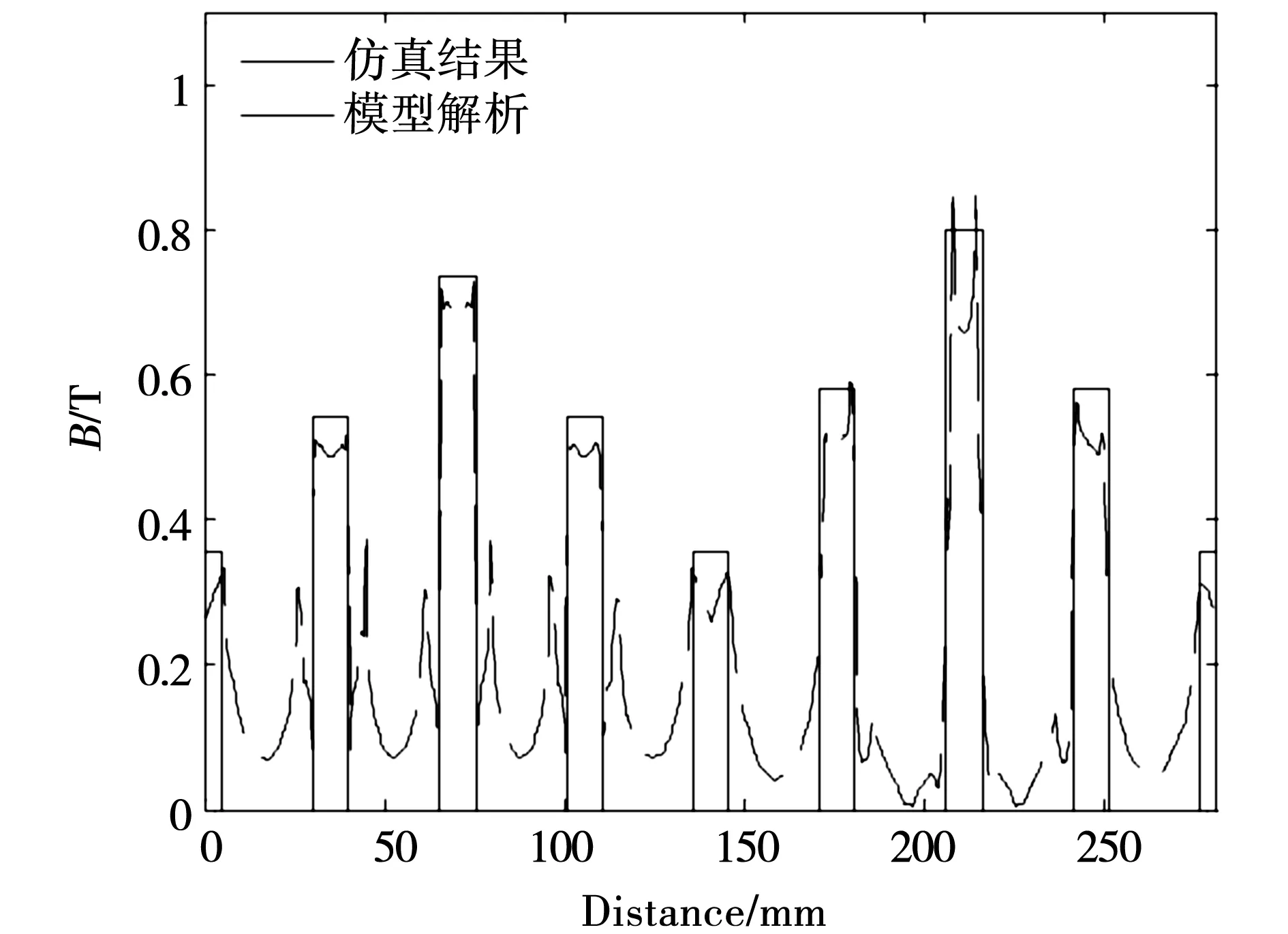
图6　气隙磁密仿真和解析结果对比Fig.6　Comparison of magnetic flux density

由图6可以看出，等效磁路模型解析计算结果和三维有限元仿真结果的分布规律基本吻合，都是以过内定子喉部的行星轮中心线呈对称分布的，其中包含耦合磁路的电磁啮合处磁密较大，未参与电磁啮合的行星轮齿处磁密较小。由模型解析求得行星轮齿与内外定子间的气隙磁密呈矩形波，这是由于磁路法是假定每段磁路的磁通沿截面均布；仿真结果较为精确地反映了三维模型中外定子齿端部和内定子电枢槽处的漏磁现象，包括除了电磁啮合处之外空间磁密很小处的漏磁，其中内侧漏磁较外侧稍小，这是因为内侧气隙磁阻相对较小；此外，在外定子侧行星轮齿处气隙磁密较内定子侧平缓，这主要是由于蜗杆内定子处存在电枢槽效应。结果对比图中的模型解析计算比仿真结果稍大，考虑到磁路模型的假设条件忽略了磁阻小量和漏磁的影响，可以认为模型解析计算结果与仿真结果的吻合度较好，验证了解析模型的准确性和可行性。

4　实验验证

为了进一步验证磁路模型对气隙磁场计算的正确性，以研制的爪式超环面电机实验样机为对象，对该样机的反电动势进行实验测量。实验样机蜗杆内定子绕组为三相12槽布线方式，采用Y型连接，每槽线圈120匝。反电动势测试平台如图7所示，右侧为实验样机，左侧为一台三相两极的异步电动机，两者通过联轴器和转速传感器同轴联接。该实验是由三相异步电动机为原动机拖动超环面电机行星架转子转动，以测得不同转速时蜗杆内定子电枢绕组输出端的相电压。

图7　样机测试平台Fig.7　Measurement system for prototype

在对实验样机的反电动势测试实验中，仅对行星架转子进行驱动，即行星轮只公转无自转，四个行星轮的初始位置在内定子喉部NS相间分布。由异步电动机拖动实验样机的爪式转子转速在835 r/min时，由示波器采集到相电压的反电动势波形如图8所示。可以看出，超环面电机的反电动势波形与正弦波类似，但期间存在部分死区，这与蜗杆内定子绕组的螺旋角度有关，螺旋角越小，死区就越少，则越接近正弦波；该转速拖动情况下，反电动势波形的最大值为16 V，测得其有效值为4.16 V；反电动势波形的周期与转速和行星轮个数有关，理论计算为35.9 ms，与测试结果相吻合。

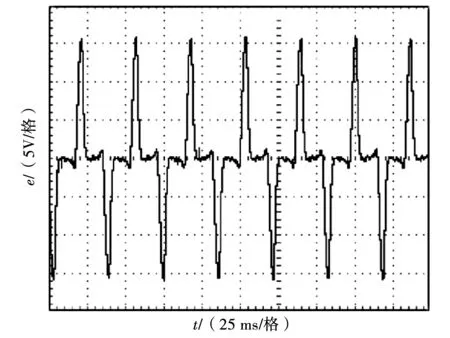
图8　样机的反电动势波形Fig.8　Wave of back electromotive force for prototype

由磁路模型计算得出的内侧气隙主磁通，可以得到行星架转子在蜗杆内定子绕组感生出的反电动势的有效值

E=4.44Nξ1Φn0Zvpn/60。

(15)

式中：Zv为内侧气隙行星轮在内定子绕组中感生电动势的当量齿数；N为内定子绕组匝数。图9所示为在不同转速下驱动行星架转子时测得超环面电机的反电动势有效值与理论计算结果对比。测试实验结果表明磁路模型计算的正确性。

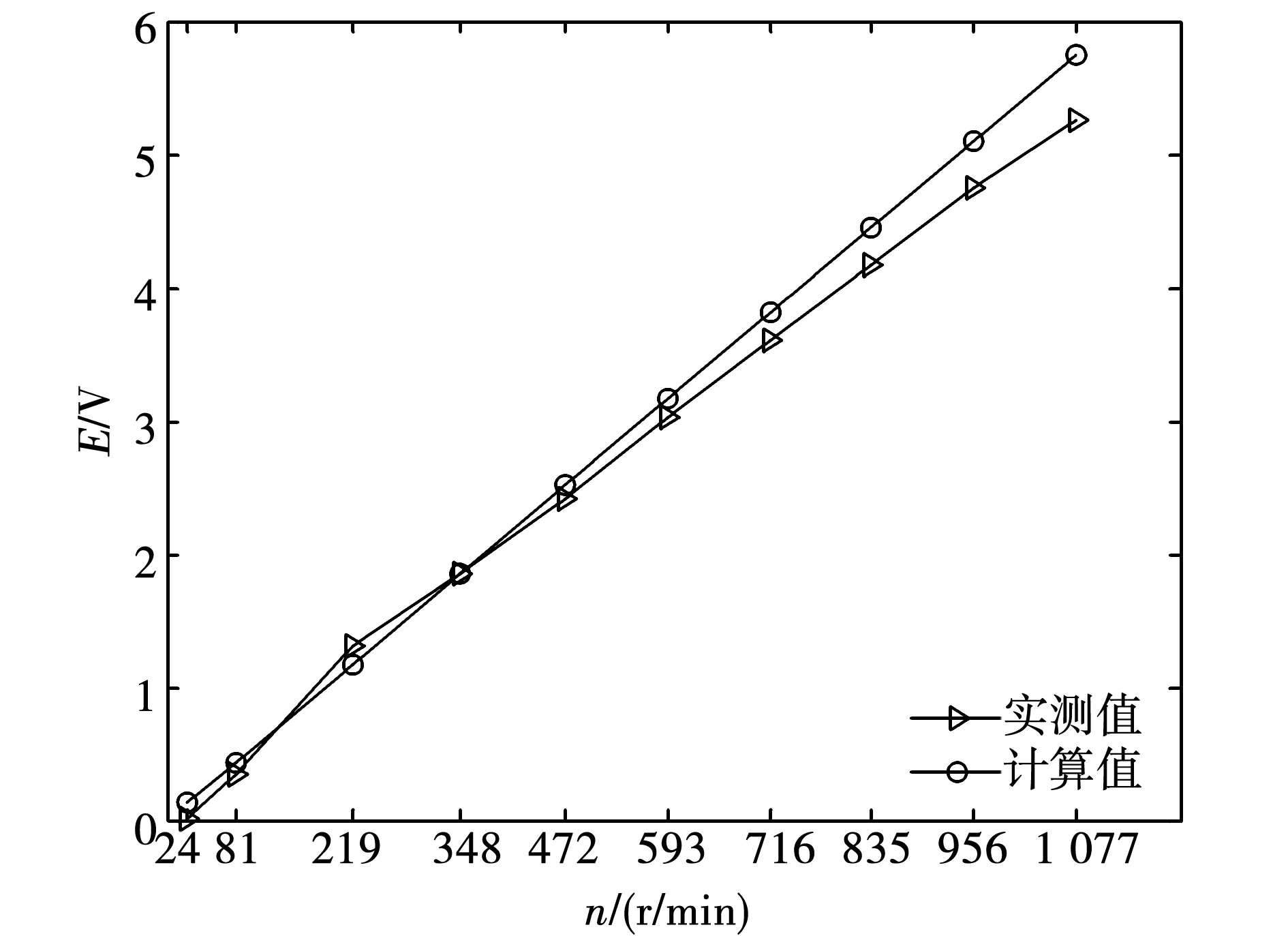
图9　反电动势计算值与测试值对比Fig.9　Comparison between calculated and test values of back electromotive force

5　结　论

本文针对双定子超环面电机的空间结构特点对其电磁驱动机理进行研究，提出了计算其爪式转子与内外定子间气隙磁场的等效磁路模型，并对其磁路的模型参数进行了详细地分析计算，求得了该电机气隙磁密的解析解。建立了该电机的三维有限元模型，仿真得到了其磁通密度云图。模型解析计算结果与仿真结果的分布规律基本一致，而且与样机反电动势测试实验所得数据吻合度较好，验证了等效磁路模型和磁场参数计算的正确性，为进一步定量分析该种新型电机的性能参数和优化电机结构设计建立了坚实的理论基础。

[1]KUEHNLE M R.Toroidal transmission and method and apparatus for making and assembling same: USP,5863273[P].1999.

[2]YAO Ligang,DAI Jiansheng,WEI Guowu,et al.Geometric modelling and meshing characteristics of the toroidal drive[J],Transactions of the ASME: Journal of Mechanical Design,2005,127(5):988-996.

[3]CAO Wenping,Mecrow B C,Atkinson G J,et al.Overview of electric motor technologies used for more electric aircraft [J].IEEE Transactions on Industrial Electronics,2012,59(9):3523-3531.

[4]ZHENG Delin,LI Huamin.Side surface harmonic stepper motor[J],Journal of Mechanical Engineering,1993,29(5):96-98.

[5]XU Lizhong.Design and torque control of an electromechanical integrating toroidal drive[J].Mechanism and Machine Theory,2006,41(2):230-245.

[6]XU Lizhong,HUANG Jin.Torques for electromechanical integrated toroidal drive[J].Proceedings of the I MECH E Part C Journal of Mechanical Engineering Science,2005,219(8):801-811.

[7]XU Lizhong,LIU Xin.Dynamic analysis of the electric system for an electromechanical integrated toroidal drive[J].Applied Electromagnetics and Mechanics,2009,30(1-2): 61-82.

[8]刘欣,许立忠,聂岭.双定子混合励磁超环面电机结构及电感参数分析[J].电机与控制学报,2014,18(10):60-67.

LIU Xin,XU Lizhong,NIE Ling.Analysis of structure and inductance on a dual-stator toroidal motor with hybrid excitation 2014[J].Electric Machine and Control,2014,18(10): 60-67.

[9]XU Lizhong,HAO Xiuhong.Dynamic response for electromechanical integrated toroidal drive to electric excitation[J].Structure Engineering and Mechanics,2007,26(6): 635-650.

[10]XU Lizhong,HAO Xiuhong.Nonlinear forced vibration for electromechanical integrated toroidal drive[J].International Journal of Applied Electromagnetics and Mechanics,2008,28(3): 351-369.

[11]XU Lizhong,HAO Xiuhong.Three DOF internal resonance for electromechanical integrated toroidal drive[J].Mechanism and Machine Theory,2012,58: 46-63.

[12]XU Lizhong,Cai Yi.Magnetic field of the worm for electromechanical integrated toroidal drive[J].Internati- onal Journal of Applied Electromagnetics and Mechanics,2007,26(1-2):51-67.

[13]ZHU Z Q,HOWE D,CHAN C C.Improved analytical model for predicting the magnetic field distribution in brushless permanent magnet machines[J].IEEE Transactions on Magnetics,2002,38(1): 229-238.

[14]张凤阁，陈进华，刘光伟，等.面贴式异向旋转双转子永磁电机的磁场解析计算[J].电工技术学报,2011,26(12):28-36.

ZHANG Fengge,CHEN Jinhua,LIU Guangwei,et al.Analytical solution of magnetic field for surface-mounted permanent magnet machines with anti-rotation dual rotors[J].Transactions of China Electrotechnical Society,2011,26(12):28-36.

[15]ZARKO D,BAN D,LIPO T A.Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J].IEEE Transactions on Magnetics,2006,42(7): 1828-1837.

[16]LIU Z J,LI J T.Accurate prediction of magnetic field and magnetic forces in permanent magnet motors using an analytical solution[J].IEEE Transactions on Energy Conversion,2008,23(3): 717-726.

[17]ZHANG Z R,YAN Y G,Yang S S,et al.Principle of operation and feature investigation of a new topology of hybrid excitation synchronous machine[J].IEEE Transactions on Magnetics,2008,44(9): 2174-2180.

[18]TAKAMICHI Yoshimoto,YASUYOSHI Asai,TOMOSHIRO Ota.Dynamic characteristics of novel two-DOF resonant actuator by vector control[J].IEEE Transactions on Magnetics,2012,48(11): 2985-2988.

[19]张凤阁,刘光伟,白海军．外永磁转子爪极电机磁路模型的建立与参数计算[J]．电工技术学报,2012,27(6): 19-24.

ZHANG Fengge,LIU Guangwei,BAI Haijun.Magnetic circuit model and parameter calculation of a claw pole machine with outer PM rotor[J].Transactions of China Electrotechnical Society,2012,27(6): 19-24.

[20]刘欣，许立忠，周守勇.超环面机电传动的结构参数及电磁啮合分析[J].机械设计，2014,31(4):55-58.

LIU Xin,XU Lizhong,ZHOU Shouyong.Analysis on structural parameters and electromagnetic meshing for toroidal electromechanical drive[J].Journal of Machine Design,2014,31(4):55-58.

(编辑：张楠)

Research on magnetic circuit model and air-gap field of dual-stator toroidal motor

LIU Xin1，XU Li-zhong2，NIE Ling1

(1.Tianjin Key Laboratory of Modern Electromechanical Equipment Technology,Tianjin Polytechnic University,Tianjin 300387,China；2.College of Mechanical Engineering,Yanshan University,Qinhuangdao 066004,China)

Dual-stator toroidal motor is a novel machine with spacial structure,and power and decelerator are integrated with good application perspective in robot and aerospace fields.Based on the analysis of its structural characteristics and operating mechanism,the three-dimensional magnetic circuit was resolved into circumferential and toroidal components,and the simplified equivalent magnetic circuit model was built.The magnetic reluctances of the model were deduced according to the structure of the motor,and the analytical solution of the air-gap magnetic flux density was obtained.In order to verify the accuracy of the magnetic circuit model,the three-dimensional magnetic field was simulated with the finite element method,and the measurement of back electromotive force for prototype was carried out.The comparison with the simulation and experimental results of the prototype machine shows that the equivalent magnetic circuit model and the calculation method of parameters are feasible,and provide theoretical foundation for further analysis of the electromagnetic properties for the motor.

dual-stator; toroidal motor; magnetic circuit model; air-gap magnetic flux density,finite element method

2015-07-14

国家自然科学基金(51207107)

刘欣(1981—)，女，博士，讲师，研究方向为超环面电机特性与控制研究；

许立忠(1962—)，男，博士，教授，博士生导师，研究方向为特种电机系统及其控制研究；

刘欣

10.15938/j.emc.2016.09.004

TM 351

A

1007-449X(2016)09-0026-07

聂岭(1990—)，男，硕士研究生，研究方向为超环面电机特性与优化设计。