数学专业复变函数论教学改革的几点建议

杨静宇

（赤峰学院　数学与统计学院，内蒙古　赤峰　024000）

数学专业复变函数论教学改革的几点建议

杨静宇

（赤峰学院数学与统计学院，内蒙古赤峰024000）

复变函数是数学专业的一门专业基础课，本文对复变函数的教学提出几点改革建议，以提高复变函数的教学.

复变函数，模块教学，对比式教学

复变函数是数学专业一门重要的专业基础课，在整个课程体系中有十分重要的作用.一方面，复变函数是数学分析的后继课程，是在实函数的基础上产生和发展起来的，很多定义、性质与实函数相似，但与实函数又有本质的区别.同时，复变函数是学习数理方程、泛函分析等课程的基础.另一方面，复变函数的理论与方法已深刻渗透到代数学、解析数论、计算数学等数学的各个分，是继续学习、深造的理论基础.所以如何让学生学好复变函数这门课程是教师们非常关心的问题.本文结合作者在教学中的体会，对复变函数教学提出几点改革建议.

1　明确培养目标，采取模块教学

在当前严峻就业形式下，我们不能够采取以往的一刀切模式进行教学，我们必须明确培养目标，根据学生的不同需求安排教学内容.通过对本院应用数学专业2014级学生的问卷调查，有60%的学生选择直接就业，有40%的学生打算考取研究生继续深造，其中有近30%的学生选择考取数学专业的研究生.针对这一调查结果，我们应将复变函数课程分为两个模块：基础模块；提高模块.

基础模块，以手中的教材为主，讲授复变函数的最基本内容.这部分内容是应用数学专业所有学生都应该掌握的.通过这部分内容的学习使学生了解复变函数的重要思想，满足后继课程对复变函数知识的需求.

提高模块，这个模块以专业选修的形式在基础模块完成后开设，36学时.这一模块主要针对考取数学类研究生的同学开设，内容主要选自外文经典书籍，甚至考虑双语教学.旨在为学生进一步深造打下坚实的基础.

2　改革教学方法

复变函数这门课程理论性强，难理解，欲取得好的学习效果一定要注意教学方法.结合自身的教学实践，我认为应做好一下几方面.

2.1上好第一堂课

数学专业课程的普遍特点是逻辑性强、枯燥乏味、难理解.尤其是复变函数，直接从实数域跨到复数域，学生们都会感觉陌生、甚至是不知所措，无从下手.很多同学学习完这门课程的感受是“知其然不知其所以然”，脑海中只留下些许的孤零零的定义、定理.造成这一现象的主要原因是“第一堂课”.第一堂课的作用在整个的教学中是不容忽视的.第一堂课教师的主要任务不是讲了教材的几页、几节，而是让学生对将要学习的这门课程有整体的了解，知道复变函数这门课程主要讲授的是解析函数，为了很好的展现解析函数教材是如何安排具体内容的，每一章的作用是什么的等等，这样就消除学生因为不了解而对这门课程产生的陌生感甚至是恐惧感，让学生条理清晰的学习这门课程.

2.2善于运用对比式教学

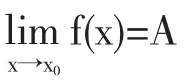
2.3注重知识的归纳和总结

复变函数论课程中概念、方法及定理非常多，及时引导学生对相关内容进行归纳总结是非常必要的.例如在讲授完解析函数后，可以将判断函数f （z）在区域D内解析的方法进行总结.

（1）定义：若f（z）在D内处处可微，我们称f（z）在D内解析.

（2）f（z）在D内解析的充要条件：函数f（z）=u（x，y）+iv（x，y）f（z）在D内解析的充要条件是

（ⅰ）二元函数u（x，y），v（x，y）在D内可微；

（ⅱ）u（x，y），v（x，y）在D内满足C.-R.方程.

（3）f（z）在D内解析的充分条件：函数f（z）=u（x，y）+iv（x，y）f（z）在D内解析的充分条件是

（ⅰ）ux，uy，vx，vy在D内连续；

（ⅱ）u（x，y），v（x，y）在D内满足C.-R.方程.

通过上述总结，学生可以很清晰、快速的判别一个具体的函数是否解析.

3　改进教学方式和手段

3.1让学生参与到教学中

学生是学习的主体，教师的作用是引导学生学习.但多数情况下我们看到的都是教师滔滔不绝的讲，学生只是被动的接收而没能参与到教学中来.学生对复变函数本来就有神秘感，教师再长篇大论的讲授，这无疑更增加了学生对这门课程的神秘感甚至是恐惧.教师应该调动学生的积极性，注重学生的主体意识，让学生参与到教学中来，或以提问的形式，或以小问题讲解的方式，拉近学生和复变函数这门课程的距离，以达到良好的教学效果.

3.2适时的借助多媒体

时至今日多媒体教学已经成为高等教育的必然趋势.但复变函数这门课程，理论性强、概念抽象、理论证明步骤复杂，所以这门课程的教学不能完全依赖多媒体，而是应以讲授和板书为主，重点难点必须在黑板上进行仔细深入的讲解，给学生留下深刻的印象.但对于有些内容，如复球面的建立、多值函数的割线等问题，在黑板上的表述不理想，借助多媒体可以形象直观的给学生呈现出来.两种教学手段的恰当结合，既丰富了教学内容，有提高了教学效率.

总之，新形势下复变函数的教学是一个不断探索的过程，需要教师全心投入，在教学内容的安排，教学方法的使用及教学手段的采取上多下功夫，以提高复变函数的教学.

〔1〕钟玉泉.复变函数论［M］.北京：高等教育出版社，2004.

〔2〕陈跃.从历史的角度引入复分析［J］.高等数学研究，2007（1）：14-17.

〔3〕华中科大数学系.复变函数与积分变换［M］.北京：高等教育出版社，2008.

〔4〕W.Rudin.Real and Complex Analysis［M］.New York，1987.

G642

A

1673-260X（2016）04-0019-02

2016-03-16