时标上动态方程的化简

刘艳花

（呼和浩特民族学院　数学系，内蒙古　呼和浩特　010051）

时标上动态方程的化简

刘艳花

（呼和浩特民族学院数学系，内蒙古呼和浩特010051）

本文主要利用时标理论讨论了时标T上一类特殊方程组的化简问题，并举例说明其方便之处，得到相应的推论.

时标；△-导数；动态方程组；化简

1　引言

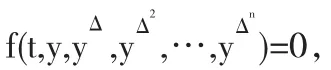
在时标T上定义两个算子σ，ρ：T→T

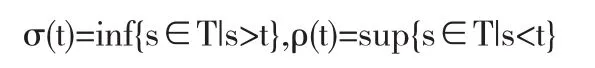
且补充定义infØ=supT，supØ=infT.

T中的点t分别称为右疏的，右稠的，左疏的，左稠的，如果σ（t）＞t，σ（t）=t，ρ（t）＜t，ρ（t）=t.

如果T中不存在左疏的最大值点，则用Tk表示T.

定义函数μ：T→［0，+∞），μ（t）=σ（t）-t

令f是时标T上的一个函数，称f在t∈Tk处是Δ—可导的，如果存在一个α，使得对任意的ε＞0，存在t的一个邻域N，使得

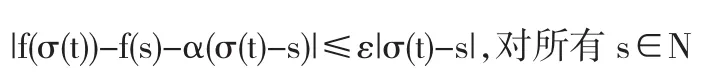
此时α记为fΔ（t）.若f在每一个点t∈Tk处Δ—可导，则称f在T上Δ—可导，且fΔ是Tk上的一个新函数.因此，如果f在r∈Tk处是Δ—可导的，则

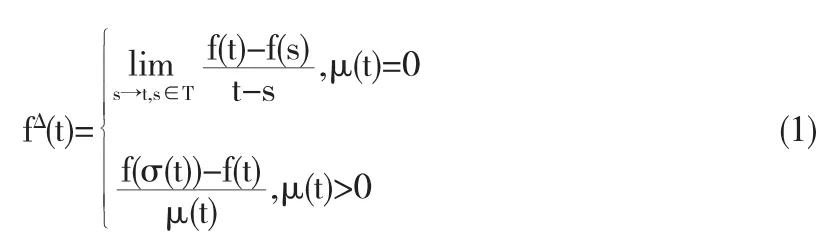
由上，若f在t∈Tk处Δ—可导，则有

在应用（2）式时，无需分别讨论μ（t）=0和μ（t）＞0的情形，该式符合这两种情形.

如果f，g是Δ—可导的，则

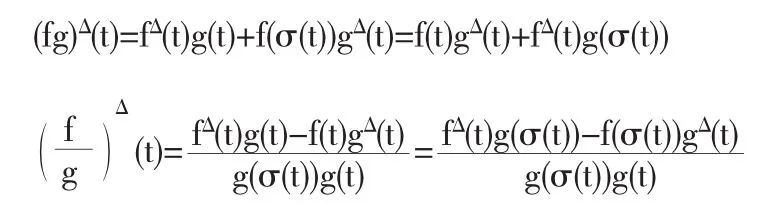
定理1可导（Δ—可导）函数是连续的.

称时标T上的函数f是rd-连续的，如果f在每一个右稠点连续且在每一个左稠点的左极限存在.

称函数p：T→R是退化的，如果对所有的t∈T，1+μ（t）p（t）≠0.

考虑初值问题

定理2如果p（t）是rd-连续的，且是退化的，则（3）有唯一解.

称（3）的唯一解为指数函数，记为ep（·，t0）

指数函数ep（t，s）的计算公式为

是一个变换.

最后，定理2可写成矩阵形式.

令P是T上的n×n函数矩阵且rd-连续，即P的每一个元素是T上的rd-连续函数.称P是退化的，如果对所有的t∈T，I+μ（t）P（t）是可逆的，这里I是n×n单位矩阵.

考虑初值问题

定理3如果P（t）是rd-连续的，且是退化的，则（5）有唯一解.

这个解称为矩阵指数，记为ep（·，t0）.若P（t）是常数矩阵A，则eA（·，t0）可计算出［3］.

2　主要结果

引理设y是时标T上的函数，则

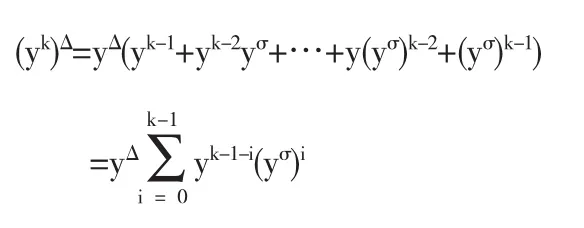
其中k是大于等于2的整数，yσ=y（σ（t）.

证明用数学归纳法证明.k=2时，（y2）△=（y·y）△=y△y+ yσy△=y△（y+yσ），等式成立.假设k=n-1时，等式也成立，即

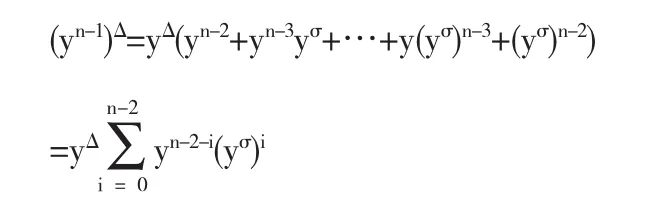
下面证明k=n时也成立.

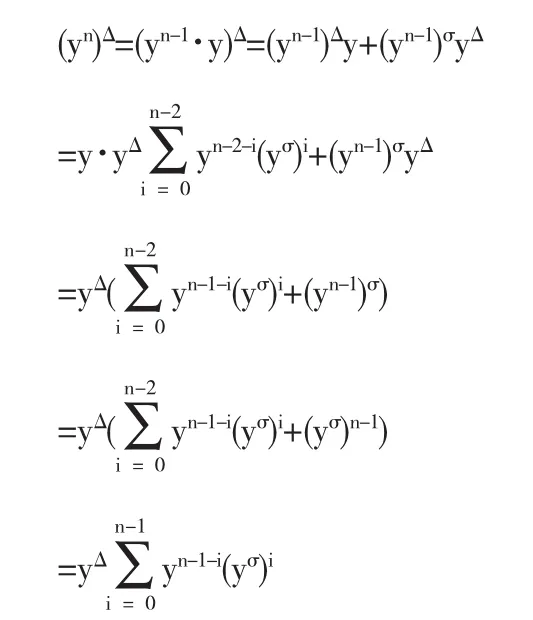
即对k=n时等式也成立.由数学归纳法，引理成立.

那么x2△=y2△=λ2y2

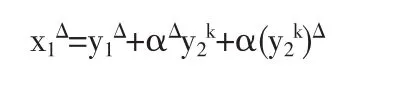
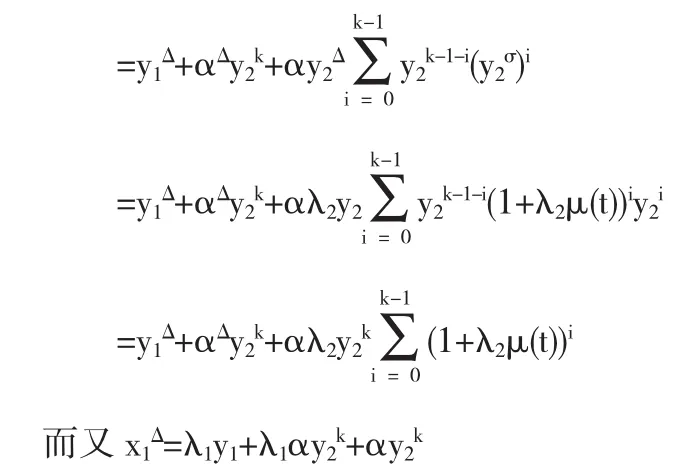
因此，由上两式得

不妨令α取方程α△=p（t）α+a的满足初值条件α（t0）=α0的解α1（t），即α=α1

定理得证.

那么（6）满足初值条件y（t0）=y0的解是

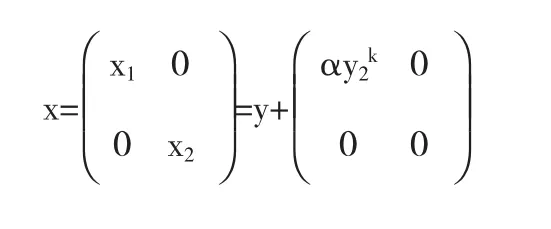
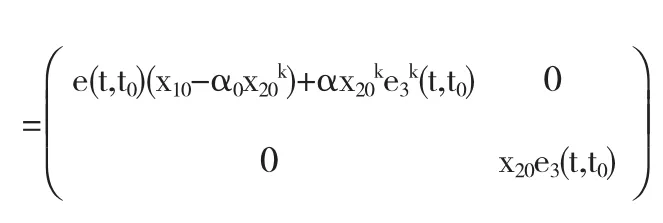
这样我们可由方程组（6）较容易的得到方程组（7）的初值问题的解.

〔1〕HilgerS.AnalysisonMeasureChainsaUnified Approach to Continuous and Discrete Calculus.Results Math.1990，18：18-56.

〔2〕AgarwalR，BohnerM，O’ReganD，PetersonA. DynamicEquationsonTimeScalesaSurvey.J. Computational and Applied Mathematic.2002，141：1-26.

〔3〕刘爱莲，朱思铭.时标上矩阵指数函数的计算［J］.应用数学学报，2008，31（6）：1056-1067.

O175

A

1673-260X（2016）04-0006-03

2015-11-12

内蒙古自治区高等学校科学研究项目（NJZY14210）