超市结算方式的优化

王颖俐，李海增

（长治学院数学系，山西长治046011）



超市结算方式的优化

王颖俐，李海增

（长治学院数学系，山西长治046011）

文章应用M/M/c/∞排队模型理论对某镇一小超市的结算方式进行优化。首先对已有数据建立已有模式和倡议模式的排队模型，进而通过对比这两种模型的排队指标，得到该超市的较优结算方式。

超市；结算方式；M/M/c/∞排队模型；排队指标

在诸如超市等一些客流量较大而结账款台较少导致需要排队等候结算服务的场所，因现行的结账方式延长了顾客排队等候的时间，造成他们不满情绪。然而如何进行结算方式结构的合理调整，一直是服务机构经营者需要解决的问题。

已有的超市结算模式是多个服务窗口独立服务，遵循先到先接受服务的原则，其中一些顾客购买的件数相对多，一些顾客购买的件数相对少，但由于服务机制的限制，那些购买件数少的顾客在需要长时间排队等候时可能会选择放弃购买而离开。能否借鉴排队论模型在其他系统，诸如企业组织结构优化[1]、银行窗口设置优化[2]、天车合理数量的确定[3]等方面的应用，对各类服务分类办理，这样可能会优化服务机制。于是笔者建立倡议模型，并通过对比两模型的排队指标，从而得出结论。

现根据某镇一小超市的数据进行分析。该超市有4个独立工作的结算台，所有结算台均适用现金或银行卡结算的方式，每个结算台为各个顾客结账的时间与该顾客所购物品件数成正比（每件约需2秒），顾客付款时约需0.5分钟。在文献[6]中已经讨论过最佳款台数量的设置，为使顾客的满意度达到最大，现倡议设其中一个为快速结账台，专门为购买4个或4个以下商品的顾客服务，另外三个款台为购买数量大于4件的顾客服务。文章将倡议模型与已有模型进行对比，从而对超市的结算方式进行优化。在文中假设顾客到达的平均时间间隔为0.5分钟，顾客购买件数遵从如下频数分布表。

表1　：2014年某超市顾客购买商品件数频率表

1　M/M/c/∞模型介绍

文章考虑M/M/c/∞排队模型[7]，在该模型中有c个结算台独立地并行服务。假定顾客的到达服从参数为λ（λ＞0）的泊松过程，若顾客到达时，结算台全部空闲，则立即接受服务；否则排队等待，直到结算台空闲接受完服务后离开。服务原则是先到先服务。

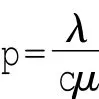
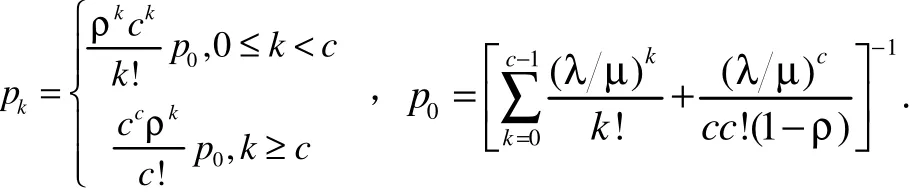
系统达到稳态时，即p＜1时，有

又由Little公式[7]，对平均等待时间和平均逗留时间有：

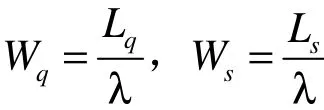
特别的，当系统中只有一个结算台时，系统变为M/M/c/∞，此时有：

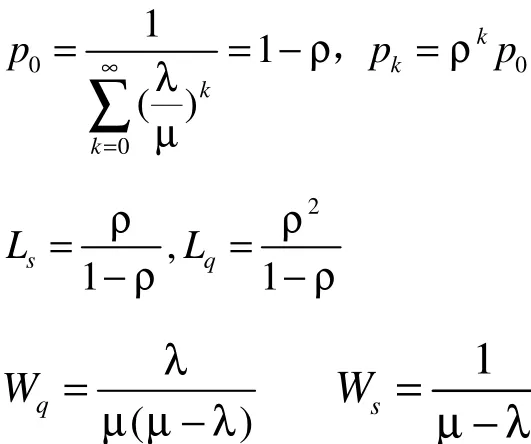
2　已有模型与倡议模型的建立

2.1已有模型

根据文章探讨的内容，该排队模型如图1所示。

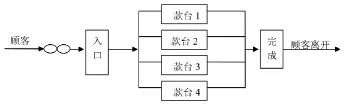
图1　已有系统的服务示意图

对于每位顾客，若设其购买N件物品的概率为PN，分析购买商品数的所有可能情况，则购买商品数在区间[ai，bi]的平均件数Ni为：

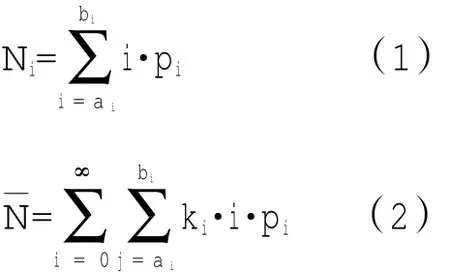
结算人员为每位顾客计算应付金额时间tN为：

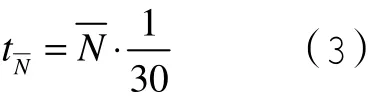
结算人员为每位顾客服务的平均时间T为：

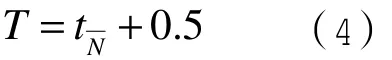
从而：

2.2倡议模型

该模型的服务示意图如下图2所示。

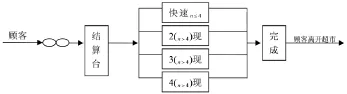
图2　倡议系统的服务示意图

对结算台1，专门为购买4个或者4个以下商品的顾客服务，对应已有模型,有：

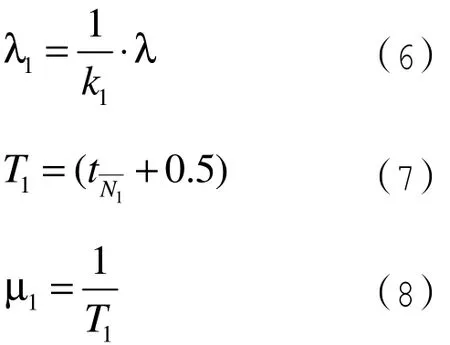
其中k1表示顾客购买商品数在第一个区间所占全部区间的比重。

对于结算台2,3,4，是为购买商品数量在4个以上的顾客结算，可得：

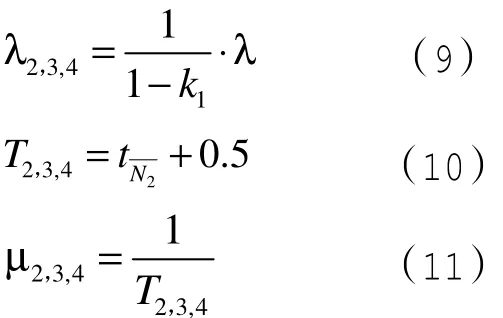
3　结论及分析

由等式（1-5）以及排队论理论知识,可得现有模型的在系统达到平衡时的一些指标，如表2所示。

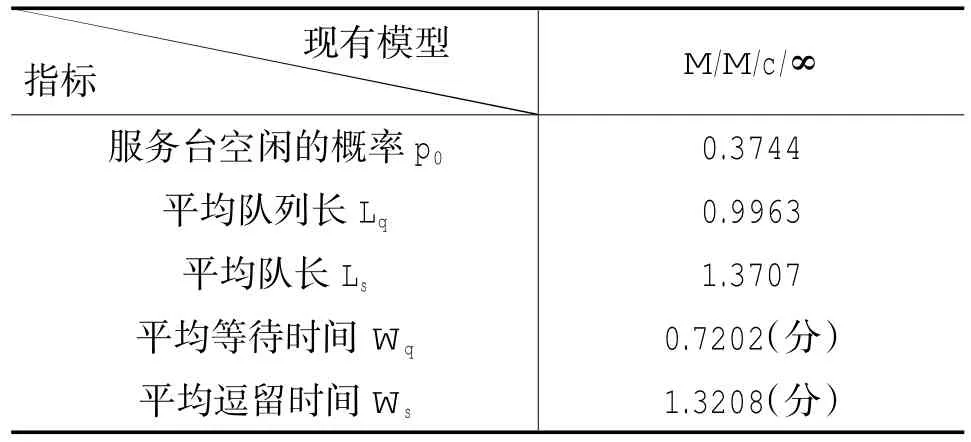
表2　已有的模型在系统达到平衡时的指标

联立等式（6-11）以及应用排队论中的M/M/1/∞及M/M/3/∞相关理论，可得倡议模型在系统达到平衡时的一些重要指标，如下表3所示。

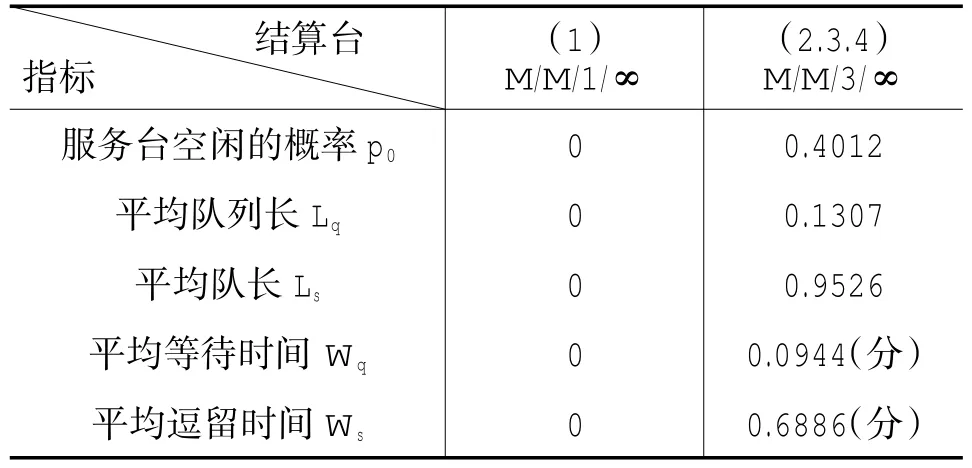
表3　倡议模型在系统平衡时的指标

对比表2和表3，可得：倡议模型比现有模型在客户满意度上有较大的改善。所以笔者的建议是：如果超市采纳了倡议模型，那么顾客的满意度将更高，从而使超市的经营效率得到很大提升。

经过计算分析发现，倡议模型使得超市的款台结算要比以往简单的多，减少了顾客的等待时间，提高了顾客对超市的满意度，能够较好的满足超市经营效益和客户满意度双赢的需求。因此，建议超市管理人员队结算台做出必要的调整，提高超市的经营效益。

［1］顾元勋.基于排队论的企业组织结构优化研究［J］,系统工程理论与实践，2000,20(12):57-62.

［2］杨米沙.银行排队系统数据分析及窗口设置优化研究［J］.武汉理工大学学报,2008,4(30):624-627.

［3］赵援.基于排队论的天车合理数量的确定［J］.物流技术,2008,27(8):217-219.

［4］徐玖平,胡知能.运筹学——数据·模型·决策（第二版）［M］.北京:科学出版社.2009.

［5］严智渊.排队论及其应用［J］.上海交通大学学报, 1980,(3):157-166.

［6］王颖俐.基于M/M/c/∞排队模型分析超市收银台数量［J］.太原师范学院学报,20015,(2)：8-10:.

［7］孙荣恒,李建平.排队论基础［M］.北京:科学出版社,2001.

［8］方兆本,缪柏其.随机过程(第三版)［M］.北京:科学出版社,2011.

（责任编辑赵巨涛）

Wang Ying-li，Li Hai-zeng
（Department of Mathematics,Changzhi University,Changzhi Shanxi,046011）

O226

A

1673-2014（2016）02-0040-03

长治学院课题（201412）。

2015—10—22

王颖俐（1987—），女，山西临汾人，硕士，讲师，主要从事时间序列分析及排队论等领域的研究。

李海增（1964—），男，山西平顺人，副教授，主要从事概率统计等领域的研究。