从数学角度讨论微功微热的意义

张拴柱

（长治学院电子信息与物理系，山西长治046011）



从数学角度讨论微功微热的意义

张拴柱

（长治学院电子信息与物理系，山西长治046011）

从数学角度出发，根据功的定义讨论微功、微热的意义，有助于深刻理解微功、微热的确切含意。

功、全微分、积分与路径无关、微功、微热

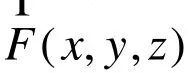
在数学上（2）式的曲线积分被称为对坐标的曲线积分。而把

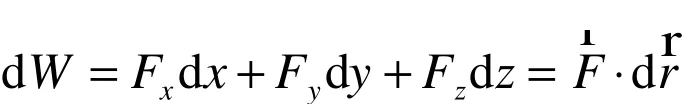
称为力F→产生元位移dr→所作的元功。由于功是过程量，因此dW看作是无限小微小过程量，但它与多元函数微积分中的全微分表达式是有区别的，因此在物理上多用dW表示，即（3）式改写为下式：

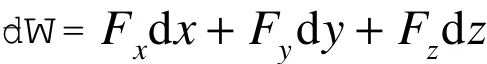
定理设G是空间开区域，且是单连通域，函数A1（x,y,z）、A2（x,y,z）、A3（x,y,z）具有一阶连续偏导数，则以下条件是等价的（即互为充要条件）

（2）积分与路径无关。若Γ1和 Γ2是两条有共同的起点和终点的曲线，则有：

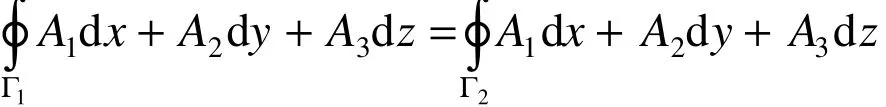
（3）A1dx+A2dy+A3dz表达式是某个函数U（x，y，z）的全微分，即：

有上面的定理可知，在物理中元功虽然写作（3）式，但并不一定就是全微分表达式，只有当表达式满足上面的条件，才能说元功表达式是某一个函数的全微分。在物理中该位置函数称为势函数U（或叫势能）即：

当元功可以表达为一个势函数的全微分时，则由上面定理可知，也就是力所作功是与路径无关。物理上则把作用于质点上的力称为保守力。因此力学中常说的保守力作功与路径无关就是定理中第（2）条所表述的。

在力学中保守力作功与路径无关，只与起点、终点位置有关，数学意义即这种力所作的功表示成曲线积分一定满足上面定理中的条件。正因为如此，在力学中，保守力作的功可以用一个状态函数即势能的改变量来表示，这样可以避免由于过程的复杂而带来计算功的困难。

在力学中最常见的自然界几种力，如：

重力

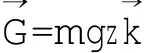
弹性力

显然符合条件（4），因此作功与路径无关，只与起点、终点位置有关。

对于万有引力和静电场中的库仑力，由于它们的大小都是与距离的平方成反比，则可写成：

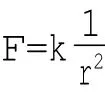
如图所示，把一个质点(或一个点电荷)放在原点处，因另一质点(或点电荷)在空间任一点P（x，y，z）处，则有

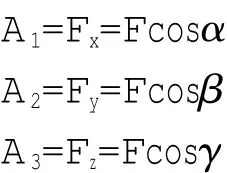
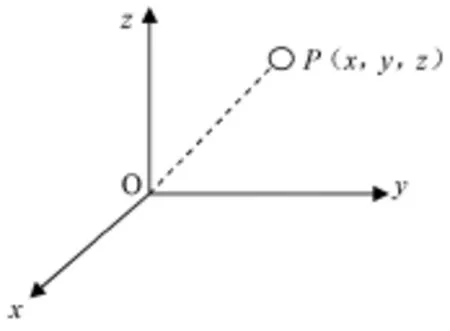
由于：

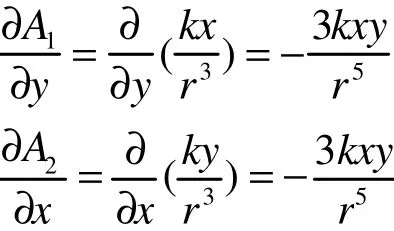
所以

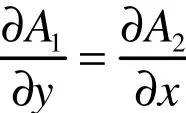
同理可证：

所以万有引力、库仑力作功与路径无关，只与起始、终了点位置有关。

在热学中，经常要讨论系统与外界之间作功、传递热量等问题，而功、热量、内能关系由热力学第一定律描述，即：

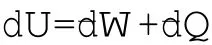
由于热量是过程量，因此微小过程中系统与外界交换微热用dQ表示，热学中我们常说微功、微热不是全微分，因此用dW、dQ表之，那么，它的确切含义指的是什么呢？

在热学中，我们知道当热力学系统处于平衡态时，系统的各种宏观量都具有确定值，而各宏观量之间存在一定的内在联系，即存在一定的函数关系，这些宏观量不可能全部都是独立变量。根据问题的性质和考虑问题的方便，选择其中几个宏观量作为自变量，这些变量足以确定系统的热力学性质，则称这些变量为状态参量，其他宏观量即可表达为状态参量的函数，即状态函数。热学中所说微功、微热不是全微分，正是以选取一组能够确定体系状态的热力学性质作为状态参量为前提条件的。

下面从数学角度来证明与微功、微热不是全微分。假如我们讨论的是一个简单的物质系统(T,V,p)由于处于平衡态时应满足物态方程，即：

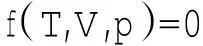
所以只有两个是独立变化的量，若选择（T，p）为独立自变量。则V=V（T，p）所以功

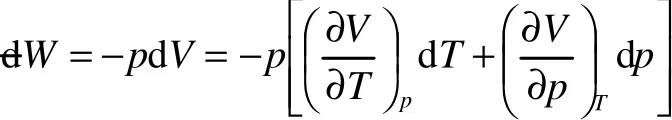
如果dW是全微分，则由定理可知，应有：

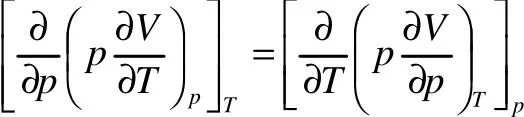
即

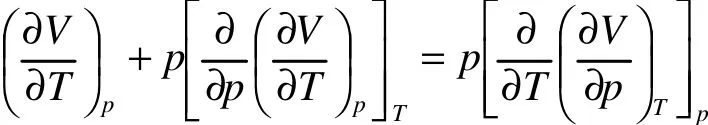
因为

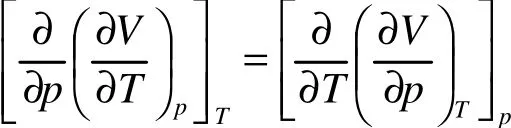
故得：

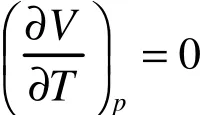
同样可以对微热展开讨论。

若选择（T，V）为独立自变量，则p=p（T，V），状态函数内能U=U（T，V），由热力学第一定律可知：

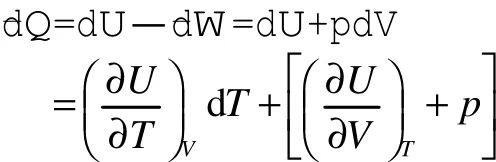
如果dQ是全微分，则由上面定理可知，应有

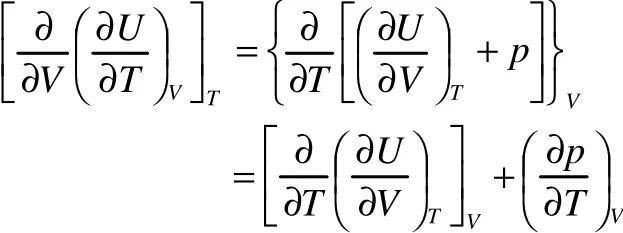
因为

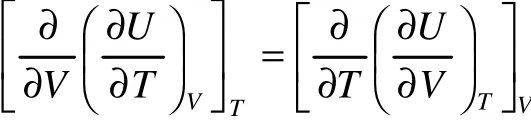
故得

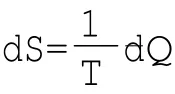
下面可以验证上面的结论。前面已知

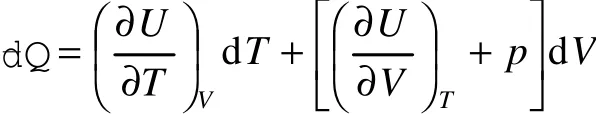
则

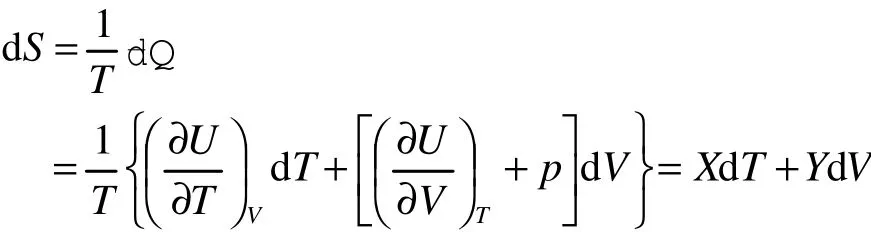
因为

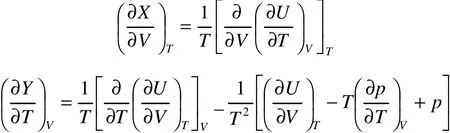
由物质内能与物态方程关系式

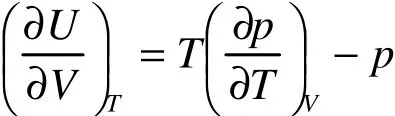
则可得

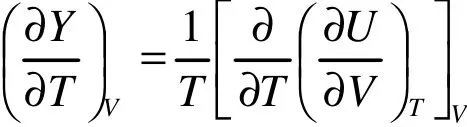
由此可得

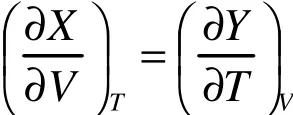
则dS确实是全微分。

由此看出，虽然dQ不是态函数，但在可逆变化过程中的dQ被温度T相除就是态函数熵的全微分，在数学上把具有这类性质的因子称为积分因子。

如果我们从数学角度看热力学中的微功、微热不是全微分是显而易见的，道理很简单。

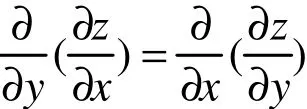
所以

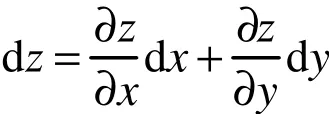
成立，但如果dz乘以它的任何一个自变量x或y即xdz或ydz它们一定不是某一个函数的全微分，即构造出的xdz或ydz不满足全微分的条件。如

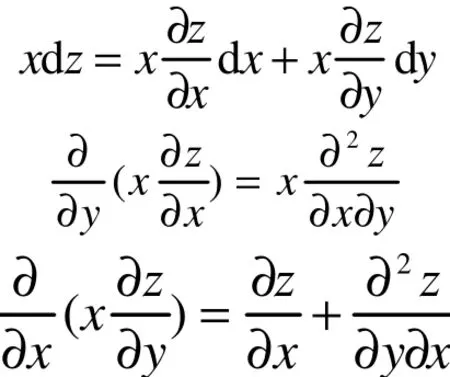
因此上面讨论的微功dW=-pdV中V=V（T，p）是状态函数，存在全微分dV，所以pdV一定不是全微分了。同理，微热为dW=TdS，而状态函数S存在全微分dS，所以TdS一定不是全微分了。

在热力学中对于简单的（T，V，p）系统，功是用状态量来表示的，即dW=-pdV，当选择（T，p）或（T，V）为独立变量，微功一定不是全微分。

［1］赵凯华，罗蔚茵.新概念物理学教程（热学）［M］.高等教育出版社，1998.

［2］秦允豪.普通物理学教程.热学［M］.第三版.高等教育出版社，2013.

［3］李椿，章立源，钱尚武.热学［M］.第二版.高等教育出版社，2008.

（责任编辑郝瑞宇）

O414

A

1673-2014（2016）02-0021-03

2016—01—05

张拴柱（1960—），男，山西晋城人，副教授，主要从事物理教学与研究。