基于DLP的自认证签密方案探讨
2016-10-10武旭升
武旭升
(西南大学数学与统计学院, 重庆 北碚 400715)
基于DLP的自认证签密方案探讨
武旭升
(西南大学数学与统计学院, 重庆北碚400715)
文章基于离散对数提出一种新的自认证签密方案,在有限域上离散对数问题的困难性假设下,新构造的方案被证明是安全的.该方案还具有保密性、不可伪造性、公开验证性、不可否认性和前向安全性等安全属性.本方案消除了证书管理和秘钥托管的安全问题且效率较高,易于实现.
自认证;签密;有限域上离散对数问题DLP;可公开验证
信息安全研究的主要目标是使消息保密又可以认证传输.传统方法“先签名后加密”所需的代价是签名和加密两部分代价之和,效率也较低.Zheng于1997年第一次提出签密的具体概念[1].签密能够在一个合理的逻辑步骤内同时完成数字签名和公钥加密两项功能,提高了效率,在计算量和通信成本方面都要比传统的“先签名后加密”降低很多,因而可以把签密看作是一种较为理想且安全的传输消息的方法.1984年,Shamir首次提出基于身份的密码体制[2].在该密码体制中,用户公钥是相应身份信息,而对应私钥则是由一可信方产生,称其为私钥生成中心(PKG).但依旧存在秘钥托管问题.1991年,Girault M首次建立自认证签密体制[3].自认证签密体制不仅解决了传统的“先签名后加密”问题,而且解决了公钥密码系统中的证书托管问题和基于身份的密码体制中的密钥托管问题.
在已有研究[4-7]和有限域上离散对数问题的难解性下,本文提出一种不依赖于椭圆曲线和双线性对的新的自认证签密方案.
1 相关困难问题
离散对数DL问题[8].设乘法群G,一个n阶元素g∈G,β是在乘法群G下以g为生成元的任意一个元素,即β∈
2 一种基于离散对数的自认证签密方案
本文提出一种基于离散对数的自认证签密方案,具体如下:


(3)PKG计算Qu=H1(yu)和xu=gxQumodq,并将(Qu,xu)发送给用户u.
(4)用户u可以通过方程yQu=xumodq验证xu的合法性,如果等式成立,进行以下步骤.
(5)私钥生成(Private Key Extract):用户u通过计算Su=ru+xH1(xu)生成私钥Su.
(6)签密(Sign Crypt):当Alice要发送消息m给Bob时,Alice执行以下操作:
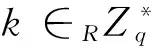
②计算V=(yByH1(yQB))kmodq;
③计算c=H3(V)⊕m;
④计算S=g-kH1(gSA)H2(m,R)modq;
⑤发送消息σ=(R,c,S).
(7)解密验证(Unsign Crypt):收到密文σ后,Bob执行以下操作:
①计算V=RSBmodq;
②恢复消息m=c⊕H3(V);
③RS=H1(yAyH1(yQA))H2(m,R)modq成立,则Bob接收消息m;否则Bob不接收m.
(8)消息正确性:
V=(yByH1(yQB))kmodq=(grBgxH1(xB))kmod
=gk[rB+xH1(xB)]modq=RrB+xH1(xB)modq=RSBmodq,
RS=gkg-kH1(gSA)H2(m,R)modq
=H1(gSA)H2(m,R)modq
=H1(grA+xH1(xA))H2(m,R)modq
=H1(grAgxH1(xA))H2(m,R)modq
=H1(yAyH1(xA))H2(m,R)modq
=H1(yAyH1(yQA))H2(m,R)modq
3 安全概念和安全性分析
3.1安全概念
一个基于离散对数问题的自认证签密方案需要具有以下安全属性:(1) 消息保密性:攻击者Oscar要想从已知的签密密文中获取任何明文信息在计算上是不可行的.(2) 密文不可伪造性:攻击者Oscar通过已知信息产生一个合法的签密密文在计算上是不可行的.(3) 第三方公开验证性:任何第三方在获取密文之后通过利用系统公开参数和签密方Alice的公钥验证等式来证明这个密文是否由Alice所签,并且验证者不能获得除该密文之外签密者Alice和接受者Bob更多的信息.(4)不可否认性:签密者Alice不能否认她之前签密过的消息.(5)前向安全性:如果签密者Alice的私钥被意外泄露或偷走,第三方也不能恢复出她已经签密消息的明文.
3.2安全性分析
定理1在有限域上离散对数问题的难解性下,除签密者Alice和密文接收者Bob外,第三方Oscar不能从密文(R,c,S)中提取出消息m,则本文方案具有消息的保密性.
证明假设攻击者Oscar已成功窃取Alice向Bob发送的已知消息m的一组密文(R,c,S),要想通过m=c⊕H3(V)恢复消息m,则必须知道V.攻击者只能通过R=gkmodq计算出k,再通过V=(yByH1(yQB))kmodq得到V.但从R=gkmodq中得出k相当于解决一个有限域上的离散对数问题,几乎是不可行的.Oscar不可能通过已获得的密文中得到明文消息m.
定理2在有限域上离散对数问题和单项散列函数求逆问题的困难性下,任何内部攻击者和外部攻击者都不可能伪造一个来自签密者Alice的关于某个消息的签密密文.本方案满足不可伪造性.
证明分内部攻击者Bob和外部攻击者两种情况.假定Bob试图通过R=gkmodq求出k之后伪造签密,相当于解决有限域上的离散对数问题,几乎是不可行的.
对于外部攻击者,在有限域上求解离散对数问题和单项散列函数的求逆问题是很困难的,想要通过等式RS=H1(yAyH1(yQA))H2(m,R)modq求出m,进而去伪造密文是不可行的.
定理3本方案具有公开验证性.
证明只需提交(R,c,S)给第三方验证者,验证者只需通过验证RS=H1(yAyH1(yQA))H2(m,R)modq是否是成立的.在验证的整个过程中并不需要Bob的私钥SB,同时也不用得到m,因此在取得保密性的基础上,第三方可以公开验证.
定理4本方案满足不可否认性.
证明只有签密者Alice才能声称密文(R,c,S)的有效性,任何第三方利用RS=H1(yAyH1(yQA))H2(m,R)modq来验证(R,S)是否是m的有效密文.因此,Bob 在不泄露其私钥SB的条件下,只要把密文(R,c,S)给第三方验证者就能够在满足公开验证性的基础上实现消息的不可否认性.
定理5在有限域上离散对数问题的难解性下本方案满足前向安全性.
证明假设在传输消息的过程中,第三方可以得到密文(R,c,S).若第三方知道Alice的私钥SA,但由于他不知道接收者Bob的私钥SB,从而不可能通过V=RSBmodq计算出V.第三方只能通过V=(yByH1(yQB))kmodq来计算V ,但必须先通过R=gkmodq计算出k,才可求出V,这是不可行的.因为从R=gkmodq中求得k相当于求解有限域上的离散对数问题.
4 结语
签密技术和自认证公钥技术是密码学中的两种新的密码技术.签密能在一个逻辑步骤内同时完成数字签名和加密两项功能.自认证签密技术使得用户的公钥无需被单独认证,而且用户的私钥由用户自己独立完成,PKG无法假冒用户,消除了密钥托管问题.本文提出一种不依赖于椭圆曲线和双线性对的新的自认证签密方案.该方案是安全的,而且具有消息的保密性、密文的不可伪造性、密文的公开验证性、不可否认性以及前向安全性等安全属性.本方案不仅不存在密钥托管问题,而且不需要使用任何公钥证书,即消除了证书存在问题,节省了大量的存储空间,相应的系统运行效率也随之提高,降低了系统的复杂性且易于实现.
[1]ZHENG Y. Digital signcryption or how to achieve cost (signature & encryption) cost (signature)+cost (encryption)[G]. Springer- Verlag, 1997:165-179.
[2]SHAMIR A. Identity-based cryptosystems and signature schemes [M]. Springer Berlin Heidelberg, 1984:47-53.
[3]GIRAULT M. Self-certified public keys[G]. Springer-Verlag, 1991:490-497.
[4]BAO F, DENG R H. A signcryption scheme with signature directly verifiable by public key[M]. Springer Berlin Heidelberg, 1998:55-59.
[5]CHANG Y S, WU T C, HUANG S C. Elgamal -like digital signature and multisignature schemes using self-certified public keys[J]. Journal of Systems and Software, 2000, 50(2):99-105.
[6]HSU C L, WU T S. Self-certified threshold proxy signature schemes with message recovery, nonrepudiation and traceability [J].Applied Mathematics and Computation, 2005, 164(1):201-225.
[7]CHANG Y F, CHANG C C, HUANG H F. Digital signature with message recovery using self-certified public keys without trustworthy system authority [J].Applied Mathematics and Computation,2005, 161(1):211-227.
[8]YU Y, MU Y, WANG G L, et al. Improved certificateless signature scheme provably secure in the standard model [J].IET Information Security, 2012, 6(2): 102-110.
(责任编辑穆刚)
Self-certified signcryption scheme based on DLP
WU Xusheng
(School of Mathematics and Statistics, Southwest University, Beibei Chongqing 400715, China)
In this paper, the author presented a new self-certified signcryption scheme based on the discrete logarithm problem, and the security analysis of the proposed scheme in the implementation plan with the random oracle model is presented in this paper. The proposed scheme has the security properties of confidentiality, non-forgeability, publicly verifiability, nonrepudiation and perfect forward security, etc. The scheme overcomes certificate management problem and key escrow problem. Moreover, it has high efficiency and is convenient to implement.
self-certified; signcryption; discrete logarithm problem (DLP); public verifiability
2016-04-06
武旭升(1990—),女,山西长治人,硕士研究生,主要从事编码理论、密码学方面的研究.
TP309
A
1673-8004(2016)05-0105-03
