泰勒展开图像插值的一个改进算法

詹　毅，李　梦

(1. 重庆工商大学数学与统计学院, 重庆　南岸　400067； 2. 重庆文理学院群与图的理论及应用重点实验室， 重庆 　永川　402160)



泰勒展开图像插值的一个改进算法

詹毅1，李梦2

(1. 重庆工商大学数学与统计学院, 重庆南岸400067； 2. 重庆文理学院群与图的理论及应用重点实验室， 重庆 永川402160)

待插像素邻域内像素点处泰勒展开式的算术平均会模糊插值图像边缘.文章提出一个改进算法，采用展开式与其灰度值之差绝对值最小的泰勒展开式近似待插像素的灰度值.这种方法充分考虑待插像素与其邻域的图像信息，获得清晰的插值图像边缘.数值实验证明：这种算法简单有效且易于实现.

图像插值；图像缩放；泰勒展开式

图像插值是由低分辨率图像通过计算机算法获得具有较高分辨率图像的技术.这种技术广泛应用于生产生活实际中，比如户外广告需要在放大数字照片的同时保持图像清晰度，图像的压缩与解压过程中分辨率的转化也需要图像插值技术，等等.如何获得光滑的图像轮廓产生清晰的图像画质，以及减少算法带来的虚像是过去几十年来图像插值技术所要解决的问题.

近年来，众多的学者提出了各种各样的算法来解决插值图像中产生的各种虚像[1-6]，比如锯齿现象、模糊以及振铃现象等.传统的双线性、双三次方法的插值函数仅仅与距离有关，不能刻画图像的局部特征信息，从而容易在图像边缘处形成模糊或锯齿现象.Hwang等人在线性模型中通过引入逆梯度权系数来增强图像边缘，以此获得清晰的图像边缘[1].但是，这种方法在插值倍数较大时会形成锯齿状边缘.NEDI算法基于低分辨协方差与高分辨率协方差的几何对偶获得高分辨图像插值[2].用小波多分辨率分析方法，Reeth等[3]运用图像边缘频率特性的无偏估计改善线性插值的效果.单方向的泰勒展开式图像插值方法是一种简单、快速的图像插值方法[4].张峥嵘等[5]运用非参数回归模型建立了一种边缘保持核回归图像插值方法，使插值图像的边缘信息得到一定的保持，但高阶导数的计算是一个比较困难的问题，这直接影响了插值图像的视觉效果. 施云惠等[6]利用再生核的数学模型特点建立了基于再生核的图像插值方法.这种方法将图像沿3个方向再生后按再生核数值积分方法导出图像插值算法来保持图像的边界信息和光滑性.计算复杂度高是这种方法的缺陷，另外，按块插值也会降低跨域两个块的图像边缘的光滑性.现代科技的发展需要插值算法简单、运算速度快，插值图像的边缘需要更清晰、更光滑.以上这些算法在实际应用中都存在各自的劣势.

本文对文献[4]的二元函数泰勒展开式模型提出一个改进算法.这种算法克服了沿各个方向泰勒展开的算法平均产生的模糊，从而产生视觉效果良好的插值图像.

1　Tayler展开式图像插值

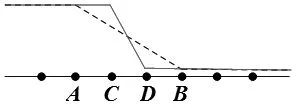
文献[4]用泰勒展开式近似数字图像的类斜面边缘减小斜坡坡度，从而抑制图像边缘的模糊程度.图1 (a) 显示了一维原始图像，现在需要在像素位置A和B之间插入 C和D 两个像素.用像素B的灰度值近似像素 D 的灰度值，像素A的灰度值近似像素C的灰度值是插值算法最理想的结果，如图1 (b)实线所示.文献[4]的基本思想是在边缘中心同侧，用已知像素(如像素点B)的泰勒展开式近似表示待插值像素(如像素点 D)：

(1)

其中，h是像素D到像素B的距离.这种方法通过减小插值图像边缘的宽度、增加边缘斜坡坡度，从而获得清晰的插值图像边缘.展开式中二阶偏导数包含了图像更多的特征信息，有利于进一步抑制插值图像的边缘锯齿现象.

(a)

(b)

图2显示了二维数字图像插值网格，实心点表示待插值像素g，空心点表示原有像素.

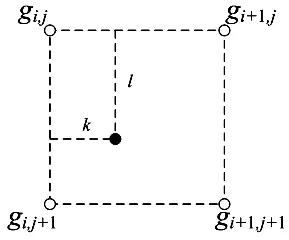
图2　插值网格

在文献[4]中，待插值像素的灰度值g分别在像素点gi,j，gi,j+1，gi+1,j，gi+1,j+1处运用二元函数的Tayler展开式获得，如用gi,j表示如下：

g(x,y)≈g(i,j)+gx(i,j)k+gy(i,j)l+

gyy(i,j)l2)

(2)

其中：gx(i, j)，gy(i, j)是g在(i, j) 处的一阶导数；gxx(i, j)，gxy(i, j)，gyy(i, j)是g在(i, j)处的二阶偏导数.类似地，可以得到在像素(i, j+1)，(i+1, j)，(i+1，j+1)处的Tayler展开表达式gi，j+1(x, y)，gi+1，j(x, y)，gi+1，j+1(x, y).文献[4]对这4个不同的表达结果进行双线性加权，得到最终插值表达式

g(x,y)=(1-l)((1-k)gi,j(x,y)+

kgi+1,j(x,y))+

l((1-k)gi,j+1(x,y)+

kgi+1,j+1(x,y))

(3)

然而， (3)式的线性加权是仍会在一个程度上模糊图像边缘.如图1(b)所示，按照(3)式，D点的像素值是用B点和A点的泰勒展开再线性加权，会与真实值之间存在误差，如图中虚线所示.

2　算法改进及实验

我们改进(3)式中待查像素灰度g(x, y)与它在像素(i, j+1)，(i+1, j)，(i+1, j+1)处的Tayler展开表达式gi，j+1(x, y)，gi+1，j(x, y)，gi+1，j+1(x, y)之间的表达式.从图1(b)可以看出，待插像素D用像素点B处的泰勒展开式比用像素点A处的泰勒展开式要更合理一些.事实上，从图中可以看出，D用B处的泰勒展开式得到的灰度近似值与B点的像素灰度值之差的绝对值要比A点处的情况小.基于此，待查像素的灰度值用某点处的泰勒展开近似处理，如果这点的泰勒展开近似与这点的灰度值之差的绝对值最小，即

g(x,y)=gi+k0,j+l0

(4)

其中：gi，j，gi，j+1，gi+1，j，gi+1，j+1是待插像素在像素(i, j), (i, j+1), (i+1, j), (i+1, j+1)处的Tayler展开表达式；gi，j，gi，j+1，gi+1，j，gi+1，j+1是在(i, j), (i, j+1), (i+1, j), (i+1, j+1)处的灰度值.

我们对全彩色boat、parrots、eye、flower图像用公式(4)进行插值，对实验结果从主观视觉和客观指标来说明提出算法的有效性.本节从主观视觉效果和客观数据指标(峰值信噪比，PSNR)来说明本文算法的有效性.

图3显示了3种算法对boat原始图像插值放大2.6×2.6倍后的结果.从图中可以看出，文献[1,4]方法产生的图像具有明显的锯齿现象以及模糊的边缘，而本文方法产生的插值图像具有较清晰的边缘.图4显示了3种算法对eye图像3×3插值的结果.从插值图像可以看出，文献[1]中方法产生锯齿现象，文献[4]虽然对抑制锯齿现象有一定效果，但边缘的模糊也是存在的.本文算法能够有效减轻图像边缘的模糊.从图5中的flower图像插值结果也可看出，在花枝的茎、梗和包裹花蕾的部分，本文算法有较好的视觉效果.表1是3种算法的峰值信噪比(psnr)的比较.从表中可以看出，本文插值算法具有较高的峰值信噪比.这与实验结果反应的视觉效果是一致的.

文献[1]算法　　　　　　　　　文献[4]算法　　　　　　　　　 本文算法

文献[1]算法　　　　　　　　　 文献[4]算法　　　　　　　　　本文算法

文献[1]算法　　　　　　　　　文献[4]算法 　　　　　　　　　 本文算法

峰值信噪比psnrBoatParrotsEyeFlower文[1]算法32.5734.1735.7934.47文[4]算法32.8435.2636.1434.52本文算法33.0335.1636.9134.60

3　结论

本文对各个方向同侧像素的泰勒展开式的最终表示进行了改进，克服了同侧泰勒展开式与异侧泰勒展开式的算法平均，获得了一个实现简单的插值方法.这种算法在抑制图像边缘的锯齿现象，获得清晰的图像边缘方面具有较好的效果.这种算法复杂度低、运算速度快，具有较好的主观视觉效果，能够很好运用于工程实践中.

[1]HWANG J W, LEE H S.Adaptive image interpolation based on local gradient features[J]. IEEE Signal Processing Letters, 2004,11(3):359-362.

[2]LI X, ORCHARD M T.New edge directed interpolation[J]. IEEE Transactions on Image Processing, 2000, 10(10):311-314.

[3]REETH E V,BERTOLINO P, NICOLAS M.Image interpolation based on a multi-resolution directional map[J]. Proceedings of the SPIE, 2011, 7870:78700M-78700M-12.

[4]詹毅.基于泰勒展开式的图像插值方法[J].计算机工程， 2012, 38(13)：202-204.

[5]张峥嵘, 刘红毅, 韦志辉. 边缘保持的核回归图像插值方法[J].计算机工程, 2011, 37(19)：194-197.

[6]施云惠, 李锌, 尹宝才.基于再生核W空间的图像插值算法[J]. 计算机仿真, 2007, 24(3)：219-222.

(责任编辑穆刚)

An improved algorithm for image interpolation with taylor expansion

ZHAN Yi1，LI Meng2

(1. Math and Statistics College, Chongqing Technology and Business University, Nan’an Chongqing 400067, China; 2. Key Laboratory of Group & Graph Theories and Applications, Chongqing University of Arts and Sciences, Yongchuan Chongqing 402160, China)

The interpolated image edges was blurred by the arithmetical average of Taylor expansion in the neighborhood of interpolated pixel. An improved algorithm is proposed. The interpolated value is the Taylor expansion which has minimum absolute of the difference with the pixel in neighborhood. This method considers image information of interpolated pixel and its neighborhood, which produce scrip edges. The numerical simulation shows that this method is simple and easy to be implemented with better visual effects.

image interpolation; image zooming; Taylor expansion

2015-09-07

国家自然科学基金项目(61202349)； 重庆市基础与前沿研究计划一般项目(cstc2013jcyjA40058， cstc2015jcyjA0142).

詹毅(1971—)，男，重庆万州人，副教授，博士，主要从事偏微分方程图像处理方面的研究.

TP391

A

1673-8004(2016)05-0008-04