(3+1)维波动方程的不变集和精确解
2016-10-10屈改珠何姝琦
陈 立, 屈改珠,2, 何姝琦
(1.西北大学 数学学院, 陕西 西安 710127; 2.渭南师范学院 数学与信息科学学院, 陕西 渭南 714000)
·数理科学·
(3+1)维波动方程的不变集和精确解
陈立1, 屈改珠1,2, 何姝琦1
(1.西北大学 数学学院, 陕西 西安710127; 2.渭南师范学院 数学与信息科学学院, 陕西 渭南714000)
为研究(3+1)维非线性波动方程的精确解,通过利用不变集方法,得到了(3+1)维非线性波动方程的一些新精确解。 该方法也可以用来求解其他非线性偏微分方程。
波动方程; 不变集; 精确解
求解偏微分方程的精确解是物理、化学、生物、经济等领域中的一个重要课题。到目前为止,已有很多种求解偏微分方程的方法,例如经典和非经典李群方法、广义条件对称法、分离变量法、不变集方法[1-8]、符号不变量和不变子空间方法[9-10]等。V. A. Galaktionov在文献[1-2]中,引入函数不变集S0={u:ux=(1/x)F(u)},讨论了KdV型方程和高阶非线性方程的精确解。屈长征和P.G.Estevez在文献[5]中,引入一般形式的不变集
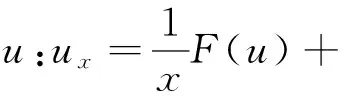
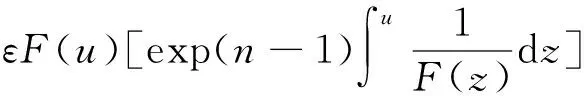
并将不变集成功地运用到一些非线性发展方程的求解中。文献[4-8]进一步推广了此方法,并得到很多有意义的结果。
本文通过建立函数不变集E0={u:ux=vxF(u),uy=vyF(u),uz=vzF(u)}研究(3+1)维非线性波动方程
utt=A(u)uxx+B(u)uyy+

其中A(u),B(u),C(u),D(u),G(u),P(u),Q(u)均为足够光滑的函数,从而求得一些新的精确解。
1 (3+1)维波动方程的精确解
考虑(3+1)维非线性波动方程
utt=A(u)uxx+B(u)uyy+C(u)uzz+
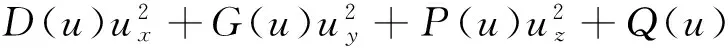
(1)
其中A(u),B(u),C(u),D(u),G(u),P(u),Q(u)均为足够光滑的函数。
引入不变集
E0={u:ux=vxF(u), uy=vyF(u),
uz=vzF(u)},
其中v(x,y,z)是x,y,z的光滑函数,F(u)是由不变条件
u(x,y,z,0)∈E0⟹u(x,y,z,t)∈E0,t∈(0,1]
所确定的光滑函数。当u∈E0时,方程有如下形式的解

利用不变集E0可以得到
ut=h′(t)F,utt=h″F+h′2FF′,ux=vxF,

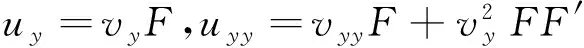
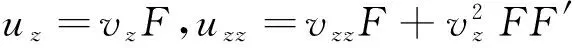
(2)
假设方程(1)在函数集E0中不变,将式(2)代入方程(1),得
h″+h′2F=Avxx+Bvyy+Cvzz+

(3)
对式(3)两端分别关于x,y,z求导,有
h′2FF″vx=Avxxx+Bvxyy+Cvxzz+
(4)
h′2FF″vy=Avxxy+Bvyyy+Cvyzz+
[A′vxx+B′vyy+C′vzz+
2(CF′+PF)vzvyz;
(5)
h′2FF″vz=Avxxz+Bvyyz+
Cvzzz+[A′vxx+B′vyy+

(6)
从式(4),(5),(6)中很难得到一般形式的解。因此,下面只考虑几种特殊情况,得到A,B,C,D,G,P,Q。
情形1vxx=vyy=vzz=0
由vxx=vyy=vzz=0,得通解为v(x,y,z)=axyz+b(xy+xz+yz)+c(x+y+z)+d。不失一般性,取a=1,b=c=d=0,即v=xyz。在此情况下,不变集E0变为
E1={u:ux=yzF,uy=xzF,uz=xyF}。
如果F″≠0,将v=xyz分别带入式(4),(5),(6)得
(BF′+GF)′x2z2+(CF′+PF)′x2y2+

(7)
(BF′+GF)′x2z2+(CF′+PF)′x2y2+

(8)
(BF′+GF)′x2z2+(CF′+PF)′x2y2+

(9)
分别对式(7)关于x求导,对式(8)关于y求导,对式(9)关于z求导,得

因此方程(1)的系数满足下面的约束条件
AF′+DF=0,BF′+GF=0,


在此种情况下,方程(1)有如下形式的解
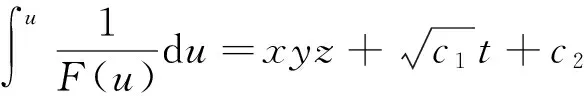
若F″=0,即F=u,也可得上述的约束条件。
令A=B=C=um,F=uk,则有
D=G=P=-kum-1,Q=c1ku2k-1。
此时,计算可得方程
utt=um(uxx+uyy+uzz)-
有精确解
由于函数v(x,y,z)=ax+by+dz(a≠0,b≠0,d≠0)为vxx=vyy=vzz=0的一个特解。若F″≠0,将v=ax+by+cz分别代入式(4),(5),(6),得
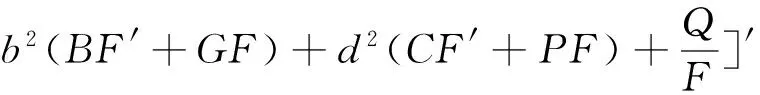
上式的左端不依赖于x,y,z,故可得A,B,C,D,G,P,Q,F满足
a2(AF′+DF)+b2(BF′+GF)+

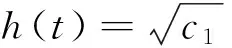
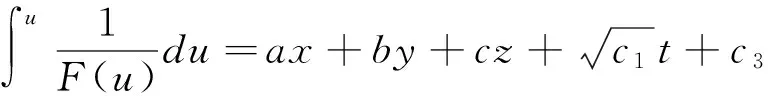
情形2vxy=vyz=vxz=0
当vxy=vyz=vxz=0时,可得v(x,y,z)=f(x)+g(y)+r(z),其中f(x),g(y),r(z)分别为x,y,z的光滑函数,此时E0变为
E1={u:ux=f′(x)F(u),uy=g′(y)F(u),
uz=r′(z)F(u)}。
在这种情况下,分以下3种情形进行讨论
情形3 f(x)=ln|x|,g(y)=ln|y|,r(z)=ln|z|
当f(x)=ln|x|,g(y)=ln|y|,r(z)=ln|z|时,v(x,y,z)=ln|x|+ln|y|+ln|z|,那么不变集为

若F″≠0,则式(4),(5),(6)变为
(10)
(11)

(12)
分别对式(10)关于x求导,式(11)关于y求导,式(12)关于z求导得

其中
(A-AF′-DF)′F];
(B-BF′-GF)′F];
(C-CF′-PF)′F]。
可得方程(1)中系数所满足的约束条件
A-AF′-DF=0,B-BF′-GF=0,



若F″=0,即F=u,依然可得上述的约束条件。
令A=B=C=um,F=uk,则D=G=P=um-k-kum-1,Q=c1ku2k-1。
计算可得方程
utt=um(uxx+uyy+uzz)+
有如下精确解
u=
情形4 f(x)=-ln|cosx|,g(x)=-ln|cosy|,r(x)=-ln|cosz|
当f(x)=-ln|cosx|,g(x)=-ln|cosy|,r(x)=-ln|cosz|时,则不变集为
E1={u:ux=tanxF(u),uy=tanyF(u),uz=tanzF(u)}。
若F″≠0,式(4),(5),(6)变为

2(A+AF′+DF)](tanx)2+
(B+BF′+GF)′F(tany)2+
(C+CF′+PF)′F(tanz)2+
2(A+AF′+DF)};
(13)

2(B+BF′+GF)](tany)2+
(A+AF′+DF)′F(tanx)2+
(C+CF′+PF)′F(tanz)2+
2(B+BF′+GF)};
(14)

2(C+CF′+PF)](tanz)2+
(A+AF′+DF)′F(tanx)2+
(B+BF′+GF)′F(tany)2+
2(C+CF′+PF)}。
(15)
对式(13)关于x求导,式(14)关于y求导,对式(15)关于z求导,得
[M′(u)F+2M(u)](tanx)3+
(2M(u)+X′(u)F)tanx=0;
[N′(u)F+2N(u)](tany)3+
(2N(u)+Y′(u)F)tany=0;
[T′(u)F+2T(u)](tanz)3+
(2T(u)+Z′(u)F)tanz=0,
其中
2(A+AF′+DF)];
2(B+BF′+GF)];
2(A+AF′+DF)];
2(B+BF′+GF)];
2(C+CF′+PF)]。
可得方程(1)的约束条件为
A+AF′+DF=0,B+BF′+GF=0,
C+CF′+PF=0,

若F″=0,即F=u,也可得上述结论。
令A=B=C=um,F=uk,则有D=G=P=-um-k-kum-1,Q=c1ku2k-1-3um+k。
计算可得方程
utt=um(uxx+uyy+uzz)-
c1ku2k-1-3um+k
有精确解
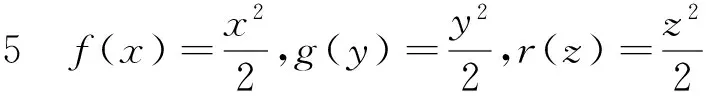
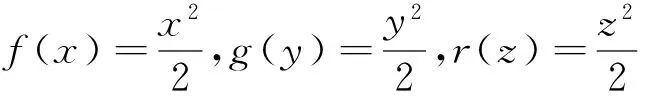
E1={u:ux=xF(u),uy=yF(u),uz=zF(u)}。
若F″≠0,可得式(4),(5),(6)分别变为
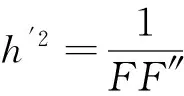
(BF′+GF)′Fy2+(CF′+PF)′Fz2+
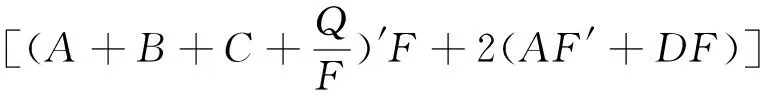
(16)

(BF′+GF)′Fy2+(CF′+PF)′Fz2+

(17)
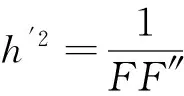
(BF′+GF)′Fy2+(CF′+PF)′Fz2+

(18)
对式(16)关于x求导,式(17)关于y求导,对式(18)关于z求导,得






可得方程(1)的约束条件为
AF′+DF=0,BF′+GF=0,CF′+PF=0,

若F″=0,即F=u,也可得上述结论。
令A=B=C=um,F=uk,则有D=G=P=-kum-1,Q=c1ku2k-1-3um+k。
计算可得方程
utt=um(uxx+uyy+uzz)-
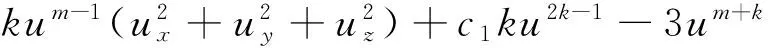
有精确解
u=
2 结 语
本文利用函数不变集E1={u:ux=vxF(u),uy=vyF(u),uz=vzF(u)},通过取v的一些特殊形式,得到(3+1)维非线性波动的精确解。值得关注的问题是,对于v还能否取更多的形式以及对应的方程会得到什么形式的精确解,有待进一步研究。
[1]GALAKTIONOV V A. Groups of scaling and invariant sets for higher-order nonlinear evolution equations [J]. Diff Integer Equation, 2001, 14(8): 913-924.
[2]GALAKTIONOV V A. Ordered invariant sets for nonlinear equations of KdV-type [J]. Compute Math Phys, 1999, 39(9): 1564-1570.
[3]QU C Z, ESTEVEZ P G. Extended rotation and scaling groups for nonlinear evolution equations [J]. Nonlinear Anal Theory Methods Appl, 2003, 52(6): 1655-1673.
[4]QU C Z. Symmetries and solutions to the thin film equations [J].J Math Anal Appl, 2006, 317(2): 381-397.
[5]ZHU C R, QU C Z. Invariant sets and solutions to higher-dimensional reaction-diffusion equations with source term [J]. Phys Lett A, 2006, 354: 437-444.
[6]QU C Z, ZHU C R. Invariant sets and solutions to the generalized thin film equations [J].Sci China A, 2007, 37(4): 447-458.
[7]QU G Z, ZHANG S L, ZHU C R. Invariant set and exact solutions to Higher-dimensional wave equations[J]. Commun Theor Phys, 2008, 49(5): 1119-1124.
[8]DONG Y Y, ZHANG S L, LI S B. Invariant sets and solutions to a class of wave equation[J]. Appl Math Comput, 2015, 253: 369-376.
[9]GALAKTIONOV V A. Quasilinear heat equations with first-order sign-invariants and new explicit solutions[J]. Nonlinear Anal Theory Methods Appl, 1994, 23: 1595-1621.
[10] GALAKTIONOV V A. Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J]. Proc Roy Soc Edinburgh, 1995, 125: 225-246.
(编辑亢小玉)
Invariant set and exact solutions to the(3+1)-dimensional nonlinear wave equation
CHEN Li1, QU Gai-zhu1,2,HE Shu-qi1
(1.School of Mathematics, Northwest University, Xi′an 710127, China;2.School of Mathematics and Information Science, Weinan Normal University, Weinan 714000, China)
To study exact solutions of the (3+1)-dimensional wave equations by employing the invariant set method. Some exact solutions of the (3+1)-dimensional wave equations are derived. This approach can also be applied to other nonlinear partial differential equations.
wave equation; invariant sets; exact solutions
2015-10-11
国家自然科学基金资助项目(11371293);渭南师范学院校级特色学科建设基金资助项目(14TSXK02);渭南师范学院理工类科研基金资助项目(15YKS005)
陈立, 女, 陕西安康人,从事偏微分方程研究。
O175.29
A
10.16152/j.cnki.xdxbzr.2016-02-004
