高二数学测试
2016-10-09
高二数学测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.已知集合A={x|x≥0},B={x|x<1},则A∩B=______.
2.复数i(2+i)的虚部为______.
3.命题:“若a≠0,则a2>0”的否命题是______.
4.若函数f(x)=2cosx,则f′(x)=______.


9.a<0是方程ax2+2x+1=0至少有一个负数根的______条件.(填必要不充分、充分不必要、必要充分、既不充分也不必要)

11.已知函数f(x)=3x|x|,且f(1-a)+f(2a)<0,则a的取值范围是______.


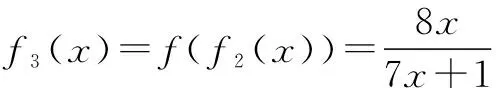

……
根据以上事实,由归纳推理可得:
当n∈N*且n≥2时,fn(x)=f(fn-1(x))=______.
二、解答题(本大题共6小题,共计90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分14分)已知复数z=1-i.
(1)设w=z(1+i)-1-3i,求|w|;

16.(本小题满分14分)定义在实数集上的函数f(x)是奇函数,g(x)是偶函数,且f(x)+g(x)=x2+ax+a(a∈R).
(1)求f(x)、g(x)的解析式;
(2)命题p:∀x∈[1,2],f(x)≥1,命题q:∃x∈[-1,2],g(x)≤-1,若p∨q为真,求a的范围.
17.(本小题满分15分)袋中装有4个黑球和3个白球,现有甲、乙两人从袋中轮流摸取一个球.甲先摸,乙后摸,然后甲再摸,……摸取后均不放回,直到有一人摸取到白球即终止.每个球在每一次被摸出的机会都是等可能的.用X表示摸球终止时所需的摸球的次数.
(1)求甲乙两人各摸一次球就终止的概率;
(2)求随机变量X的概率分布列和数学期望E(X).
18.(本小题满分15分)某单位用3 240万元购得一块空地,计划在该地块上建造一栋至少15层的小高层、每层3 000平方米的楼房.经测算,如果将楼房建为x(x≥15)层,则每平方米的平均建筑费用为840+kx(单位:元).已知盖15层每平方米的平均建筑费用为1 245元.
(1)求k的值;

19.(本小题满分16分)定义在[a,b]上的函数f(x),若存在x0∈(a,b)使得f(x)在[a,x0]上单调递增,在[x0,b]上单调递减,则称f(x)为[a,b]上的单峰函数,x0为峰点.
(1)若f(x)=-x3+3x,则f(x)是否为[0,2]上的单峰函数,若是,求出峰点;若不是,说明理由;
(2)若g(x)=m·4x+2x在[-1,1]上不是单峰函数,求实数m的取值范围;
(3)若h(x)=|x2-1|+n|x-1|在[-2,2]上为单峰函数,求负数n的取值范围.
20.(本小题满分16分)已知函数f(x)=x2-2alnx(a∈R),g(x)=2ax.
(1)求函数f(x)的极值;
(2)若a>0,函数h(x)=f(x)-g(x)有且只有一个零点,求实数a的值;
(3)若0
参考答案
一、填空题
1.[0,1);2.2;3.若a=0,则a2≤0;
4.-2sinx;5. 2; 6.4;7.3或6;


二、解答题
15.(1)∵z=1-i,
∴w=(1-i)(1+i)-1-3i=1-3i,

(2)由题意,得
z2+az+b
=(1-i)2+a(1-i)+b
=a+b-(2+a)i,

16.(1)由f(x)+g(x)=x2+ax+a,
①
得f(-x)+g(-x)=x2-ax+a.
因为f(x)是奇函数,g(x)是偶函数,
所以f(-x)=-f(x),g(-x)=g(x),
所以-f(x)+g(x)=x2-ax+a,
②
①②联立得f(x)=ax,g(x)=x2+a.
(2)若p真,则f(x)min≥1,得a≥1;
若q真,则g(x)min≤-1,得a≤-1.
因为p∨q为真,所以a≥1或a≤-1.

(2)袋中的7个球 3白4黑,随机变量X的所有可能取值是1,2,3,4,5.

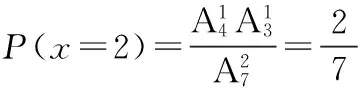



随机变量X的概率分布列为:
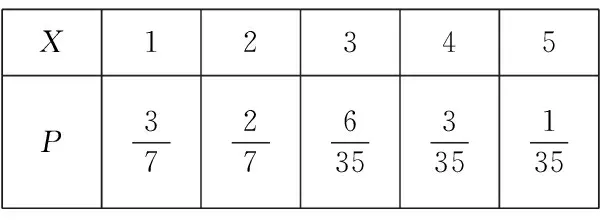
X12345P3727635335135

18. (1)由题840+15k=1 245,解得k=27.
(2)设楼房每平方米的平均综合费用为f(x)元,则




x(0,20)x=20(20,+∞)f'(x)-0+f(x)递减极小值递增
所以当x=20时,f(x)有最小值.
答:为了使楼房每平方米的平均综合费用最少,该楼房应建为20层.
19. (1)令f′(x)=-3x2+3=0,得x=±1.当0≤x<1,f′(x)>0,1 (2)先考虑g(x)=m·4x+2x在[-1,1]上是单峰函数. (3)h(x)= 综上,n≤-4. 当a≤0时,f′(x)>0,f(x)在(0,+∞)上递增,f(x)无极值. 综上, 当a≤0时,函数f(x)无极值;当a>0时,f(x)极小值=a-alna,无极大值. (2)令h(x)=x2-2alnx-2ax,则 ∵a>0,∴令h′(x)=0,得 ∴h(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增, ∴h(x)在x0处取得极小值h(x0)=0.