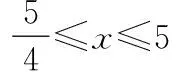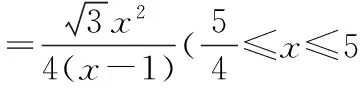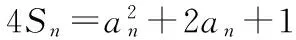高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题，每小题5分，共70分)

2.不等式|3x+1|>2的解集为______.

3.在∆ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=______.

4.等比数列{an}中,若a1=1,a4=8,则该数列的前10项之和为______.

5.一个圆锥的轴截面是个边长为2的正三角形,这个圆锥的侧面积等于______.

6.已知点P(x,y)在不等式组

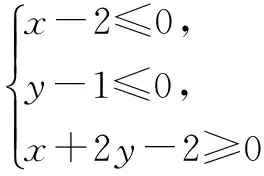
表示的平面区域上运动,则z=x-y的取值范围是______.

7.如果在等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=______.

8.m,n是不同的直线,α，β，γ是不同的平面，有以下四个命题

其中正确的命题是______.

11.已知∆ABC的一个内角为 120°,并且三边长构成公差为4的等差数列,则∆ABC的面积为______.

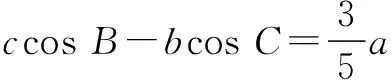
二、解答题(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.

(1)求a,b;

(2)解不等式(x-c)(ax-b)>0.

16.(本小题满分14分)在∆ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列.

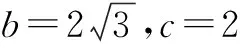
(2)若sinA, sinB, sinC成等比数列,试判断∆ABC的形状.

17.(本小题满分15分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.

(1)求证:CD∥平面PAB;

(2)求证:PE⊥AD;

(3)若CA=CB,求证:平面PEC⊥平面PAB.

18.(本小题满分15分)已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3,a5-3b2=7.

(1)求{an}和{bn}的通项公式;

(2)设cn=an·bn,n∈N*,求数列{cn}的前n项和Sn.

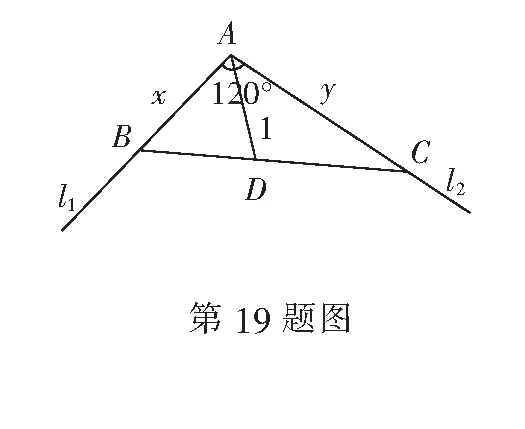
19.(本小题满分16分)如图,某水域的两直线型岸边l1,l2成定角120°,在该水域中位于该角角平分线上且与顶点A相距1公里的D处有一固定桩.现某渔民准备经过该固定桩安装一直线型隔离网BC(B,C分别在l1和l2上),围出∆ABC养殖区,且AB和AC都不超过5公里.设AB=x公里,AC=y公里.

(1)将y表示成x的函数,并求其定义域;

(2)该渔民至少可以围出多少平方公里的养殖区?

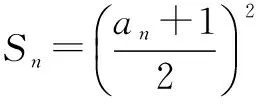
(1)求数列{an}的前n项和Sn;

(2)记数列bn=an+λ,n∈N*,λ∈R,其前n项和为Tn.

① 若数列{Tn}的最小值为T6,求实数λ的取值范围;

参考答案

一、填空题

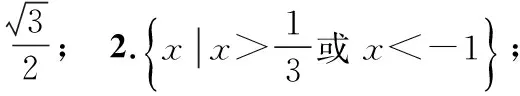
6.[-1,2];7.28;8.① ③;

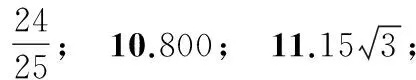
二、解答题

15.(1)由已知，1是方程ax2-3x+2=0的根,则a=1,∴方程为x2-3x+2=0⟹b=2,因此,a=1,b=2.

(2)由(1)可知,原不等式为

(x-c)(x-2)>0.

当c<2时，解集为{x|x2};

当c>2时，解集为{x|x<2或x>c};

当c=2时，解集为{x|x≠2}.

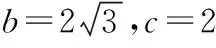
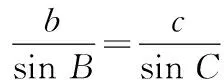
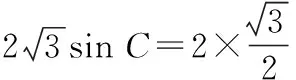
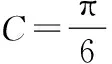
(2)因为sinA,sinB,sinC成等比数列，所以

sin2B=sinAsinC.

由正弦定理，得b2=ac；由余弦定理，得

b2=a2+c2-2accosB=a2+c2-ac,

所以ac=a2+c2-ac,即(a-c)2=0,a=c.

17.(1)因为底面ABCD是菱形,所以CD∥AB.又因为CD⊄平面PAB,且AB⊂平面PAB,所以CD∥平面PAB.

(2)因为PA=PB,点E是棱AB的中点,所以PE⊥AB.因为平面PAB⊥平面ABCD,PE⊂平面PAB,所以PE⊥平面ABCD.

因为AD⊂平面ABCD,所以PE⊥AD.

(3)因为CA=CB,点E是AB的中点,所以CE⊥AB.由(2)可得PE⊥AB，又因为CE∩PE=E,所以AB⊥平面PEC.

而AB⊂平面PAB,所以平面PAB⊥平面PEC.

18.(1)设{an}的公比为q,{bn}的公差为d,由题意q>0.由已知,有

消去d得q4-2q2-8=0,解得q=2,d=2.

所以{an}的通项公式为an=2n-1,n∈N*,{bn}的通项公式为bn=2n-1,n∈N*.

(2)由(1)，有cn=(2n-1)2n-1.

设{cn}的前n项和为Sn,则

Sn=1×20+3×21+5×22+…+(2n-1)·2n-1,

2Sn=1×21+3×22+5×23+…+(2n-1)·2n,

两式相减得-Sn=1+22+23+…+2n-(2n-1)·2n=-(2n-3)×2n-3,

所以Sn=(2n-3)2n+3.

19.(1)由S∆ABD+S∆ACD=S∆ABC,得

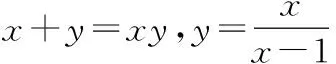
又0

(2)设∆ABC的面积为S,则结合(1)，易得

S=xysinA

①

②

②-①，得

2(an+1+an)=(an+1+an)(an+1-an).

由题知an+1+an≠0,得an+1-an=2.

得a1=1,an=2n-1,Sn=n2.

(2) ① 由bn=2n-1+λ,得Tn=n2+λn的最小值为T6,得Tn≥T6, 得n2+λn≥T6=36+6λ,

② 因为{bn}是“封闭数列”,设

bp+bq=bm(p,q,m∈N*,且任意两个不相等),∴2p-1+λ+2q-1+λ=2m-1+λ,

∴λ=2(m-p-q)+1,λ为奇数.

由任意n∈N*,都有Tn≠0,且

即λ的可能值为1,3,5,7,9.

又Tn=n2+λn>0,

检验得满足条件的λ=3,5,7,9,

即存在这样的“封闭数列” {bn},使得对任意n∈N*，都有Tn≠0,且

所以实数λ的所有取值集合为{3,5,7,9}.