十字型阵列MIMO雷达高精度二维DOA估计

梁　浩　崔　琛　余　剑

（合肥电子工程学院通信对抗系401室 合肥 230037）

十字型阵列MIMO雷达高精度二维DOA估计

梁浩*崔琛余剑

（合肥电子工程学院通信对抗系401室 合肥 230037）

该文针对十字型阵列配置下的单基地MIMO雷达2维空间角度估计问题，提出一种新的基于酉变换的高精度估计算法，算法利用收、发阵列中十字型阵列的中心对称性，通过酉矩阵设计及酉变换过程，将发射、接收阵列中对应的长、短基线平移不变关系映射到实数域，并基于双尺度酉ESPRIT算法实现2维参数的无模糊高精度估计。仿真结果表明：该文算法不牺牲阵列孔径，在获得2维空间角度无模糊高精度估计的同时，无需额外的配对算法和谱搜索；与传统酉变换过程相比，该文算法的酉变换过程等效将发射与接收导向矢量分别实数化，有效克服了传统酉变换算法中实数域旋转不变因子无法提取的问题，在实现特征分解与参数求解完全实数化的同时，具有更低的运算复杂度。最后，通过仿真实验验证了该文算法的正确性和算法的有效性。

MIMO雷达；十字型阵列；酉变换；双尺度酉ESPRIT

引用格式：梁浩，崔琛，余剑.十字型阵列MIMO雷达高精度2维DOA估计［J］.雷达学报，2016，5（3）：254-264.DOI：10.12000/JR16016.

Reference format：Liang Hao，Cui Chen，and Yu Jian.Two-dimensional DOA estimation with high accuracy for MIMO radar using cross array［J］.Journal of Radars，2016，5（3）：254-264.DOI：10.12000/JR16016.

1　引言

以多输入多输出（Multiple Input and Multiple Output，MIMO）技术为基础体制的MIMO雷达系统，因其在目标检测、参数估计、杂波抑制等方面具有诸多优势［1，2］，已成为现代雷达发展趋势的综合体现，引起国内外学者的高度关注。根据信号处理方式的不同，MIMO雷达可以分为分布式MIMO雷达和集中式MIMO雷达；本文以集中式MIMO雷达为研究对象，重点研究单基地配置下的多目标参数估计问题。

单基地配置下的集中式MIMO雷达利用匹配滤波技术，能够在接收端综合收、发阵列孔径，获取比传统相控阵雷达更大的孔径扩展，因此在目标分辨能力和参数估计性能方面优势明显。为了获取目标参数的有效估计，传统基于相控阵雷达的高分辨算法被广泛应用于目标参数估计中。文献［3］通过设计相应的降维矩阵，将原始单基地MIMO雷达高维回波数据转换到了低维信号空间，去除了虚拟扩展中所有的冗余数据，因此降低了后续处理的数据维数，但其参数求解涉及1维Capon谱搜索；文献［4］在进行降维变换之后，直接利用ESPRIT算法进一步避免了谱搜索；文献［5，6］在文献［4］的基础上进一步通过酉变换，充分利用复观测数据及其共轭数据来提高ESPRIT算法的参数估计精度，在不增加阵元的情况下，提高了算法的估计性能，同时通过实值运算，也进一步降低了整体的运算复杂度；但以上研究局限于1维线阵模型，无法获取多维方位信息实现目标方向的定位。

事实上，当收、发阵列均采用2维（或更高维）阵列配置时，目标参数维度的扩展意味着目标特征描述得更加准确，同时收、发阵列经过MIMO雷达虚拟扩展后整体天线流型也就更为复杂，因此深入研究2维天线配置下单基地MIMO雷达的虚拟扩展性能以及参数估计问题对目标的定位具有重要意义。文献［7，8］基于单基地MIMO雷达3维阵列配置模型，对比分析了不同平面流型配置下基于最大似然估计算法的MIMO雷达天线位置敏感性和模糊限，重点考虑阵列几何形状对MIMO雷达虚拟阵列流形的影响，分析比较了不同阵列配置下MIMO雷达总的敏感性测度；文献［9］进一步通过MIMO虚拟阵列流形的微分几何性质，研究了MIMO雷达估计精度、检测及分辨的性能极限，并对比了几种典型天线几何配置下MIMO雷达系统的测向性能，为MIMO雷达系统的天线设计提供了依据。但文献［7-9］的研究集中在2维阵列配置对MIMO雷达测向性能的影响。文献［10］研究了双平行线阵配置下单基地MIMO雷达的2维参数估计问题，提出了降维（RD）ESPRIT算法，该模型尽管进行了降冗余处理，但只能实现1维方向上的阵列扩展；文献［11］研究了L型阵列配置下单基地MIMO雷达的2维参数估计问题，算法通过构造降维矩阵对回波数据进行降维预处理后，利用二次优化方法将2维DOA估计分解为两个1维DOA估计，一定程度上降低了运算复杂度，但降维矩阵的设计并没有最大程度地降低回波数据的维数，回波数据中仍存在冗余；同时参数求解过程中两次1维谱搜索仍存在较高的运算量；文献［12］针对文献［11］存在的问题，利用L型阵列配置对应的虚拟阵列的对称性，通过重新设计降维矩阵，去除了所有冗余数据，并利用ESPRIT算法在不牺牲阵列孔径的条件下实现2维DOA的有效估计，避免了谱搜索；文献［13］研究了平面阵配置下的单基地MIMO雷达的2维参数估计问题，通过降维矩阵的设计以及降维处理，并针对降维后阵列流型与双基地MIMO雷达的等效相似性，利用文献［14，15］中的酉变换思想进行实数域信号子空间估计和2维参数求解，其降维矩阵的设计以及降维过程本质上为文献［3-6］中1维降维变换在2维上的扩展应用，同时由于采用面阵配置，面临着巨大硬件成本和复杂代价。以上算法尽管能够实现单基地MIMO雷达1维/2维目标角度的有效估计，但大多要求收、发阵列阵元间距满足半波长的限制，本质上仍属于角度参量在短基线阵元间距上的度量。

众所周知，阵列的孔径决定着雷达的分辨性能和测向精度，阵元间的基线扩展（大于半波长）能够有效增大阵列的整体孔径，提高参数估计的性能和精度，但会带来方位估计的周期性模糊。本文针对单基地MIMO雷达的2维测向问题，提出一种具有2维双尺度平移不变特性的收、发十字型阵列设计，并针对传统DR-UESPRIT算法求解过程中存在的实数域旋转不变因子无法提取的问题，提出一种新的基于酉变换的高精度估计算法，算法利用收、发阵列中十字型阵列的中心对称性，通过酉矩阵设计及酉变换过程，将发射、接收阵列中存在得长、短基线平移不变关系映射到实数域，并基于双尺度酉ESPRIT（Dual-Resolution Unitary ESPRIT，DR-UESPRIT）算法实现2维参数的高精度无模糊估计，同时不牺牲阵列孔径，无需额外的配对算法和谱搜索，能够实现特征分解与参数求解完全实数化，具有更低的运算复杂度。

2　问题建模

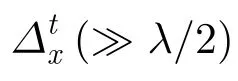
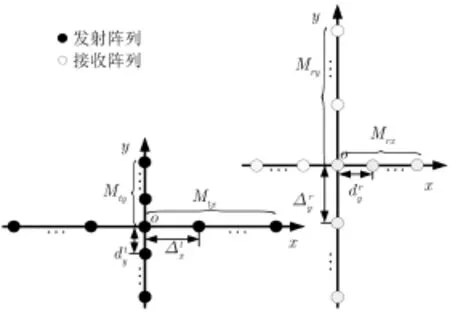
图1　单基地 MIMO 雷达收、发阵列结构示意图Fig.1　Transmit/receive array structure for monostatic MIMO radar

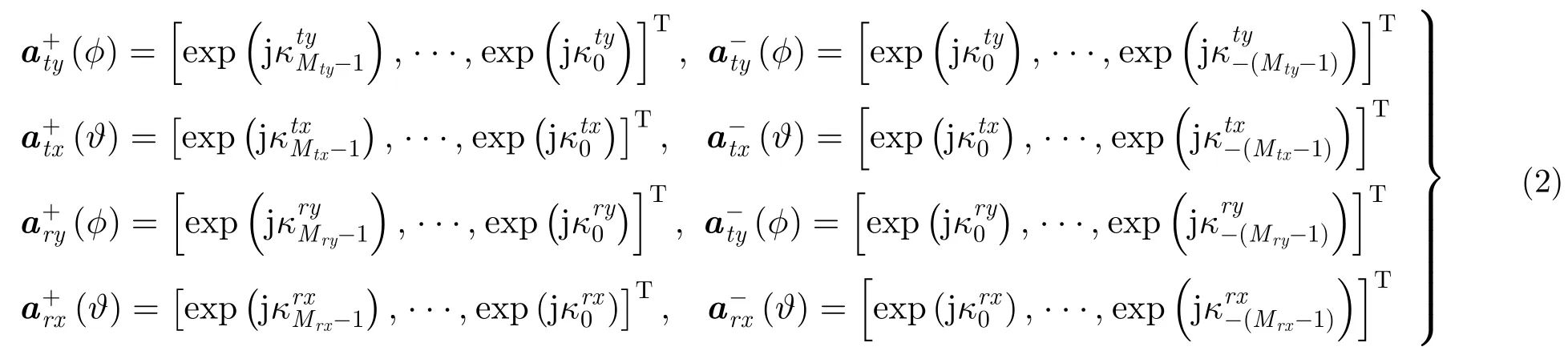
其中

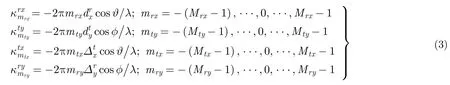
由于发射正交波形，则接收的回波信号经过匹配滤波以及矢量化操作后，可得第 l 次快拍的接收数据：

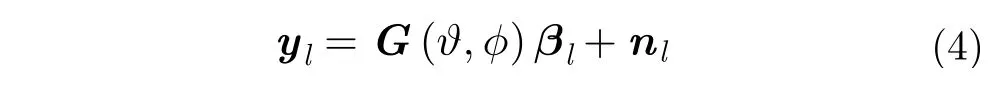
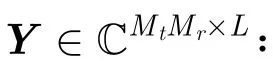
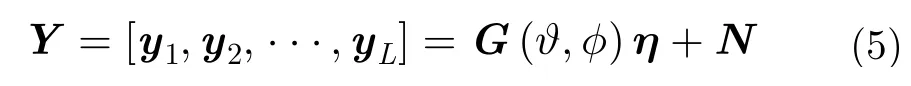
3　基于酉变换的高精度2维角度联合估计

3.1酉矩阵设计及实信号子空间估计

由信号模型和式（5）可得，发射、接收对应的流型矢量满足：

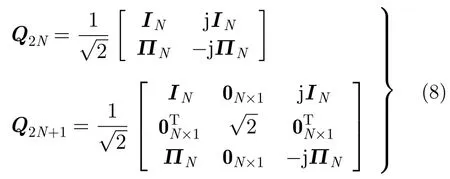
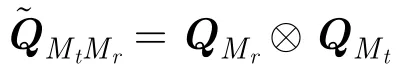
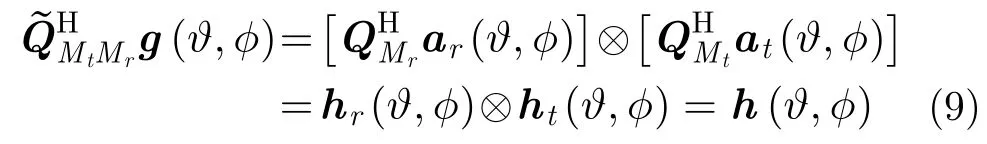
显然，h（ϑ，φ）为g（ϑ，φ）在实数域对应的流型矢量，同时由上式可以看出，通过酉变换转换为实数域后，发射与接收导向矢量Kronecker积的关系并没有改变，这就为后续在实数域分别通过发射与接收矢量，提取长短基线的平移不变关系提供了条件。在进行实数域信号子空间估计之前，需要构建相应的Centro-Hermitian矩阵，即通过回波数据协方差矩阵（Covariance Matrix，CM）的前后平滑构建可得：

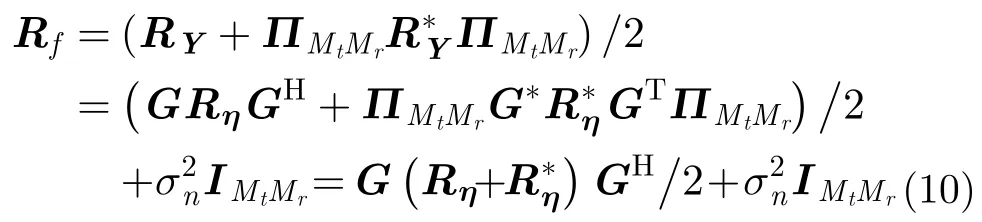
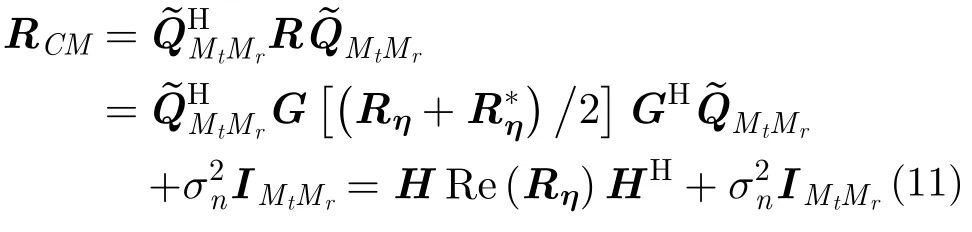
3.2高精度2维DOA的联合估计

3.2.12维角度的粗估计与精估计发射、接收阵列中x，y轴向上的短基线阵元间距可以获得2维角度的无模糊粗估计，同时发射、接收阵列中x，y轴向上的长基线阵元间距可以获得2维角度的高精度估计，对应的平移不变关系分别为：

则式（13）对应的实数域平移不变关系为：

同时易证得：

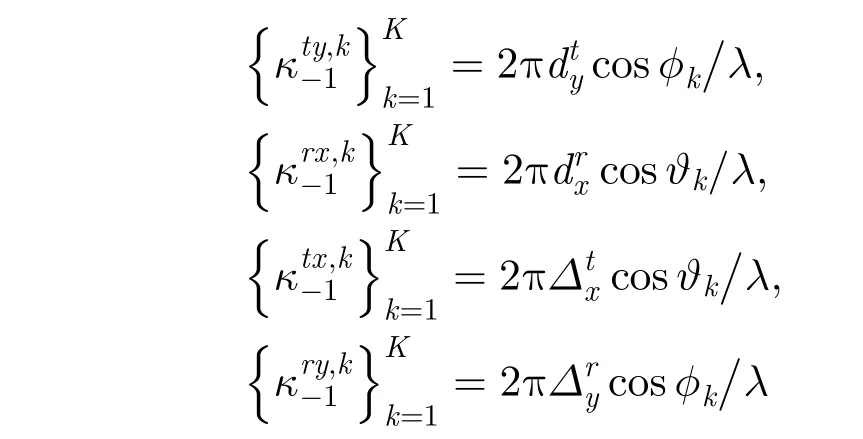
由式（12）和式（21）可得：

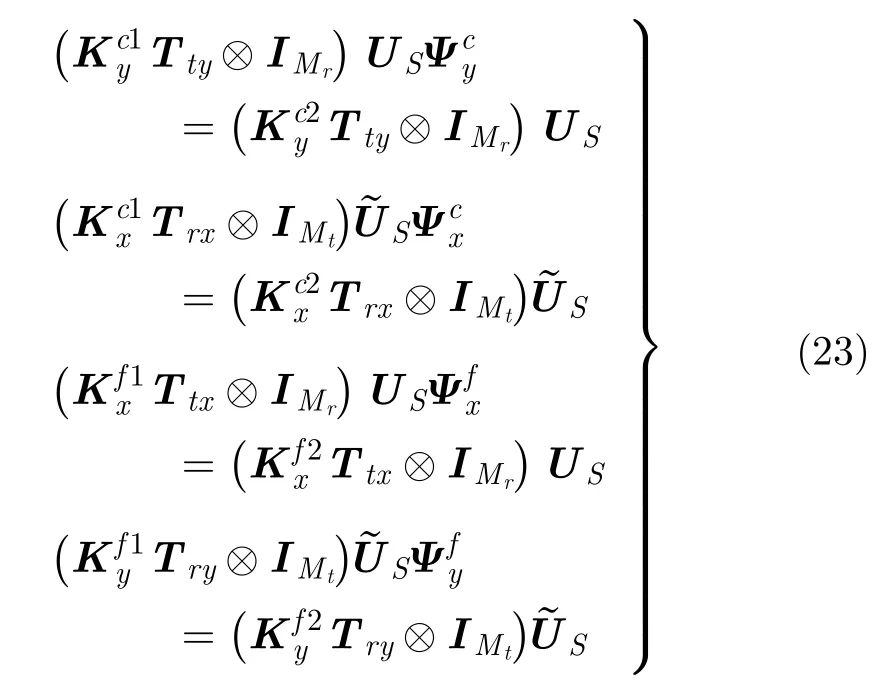
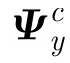
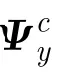
进一步代入式（24）可得：

利用矩阵P进一步构造：

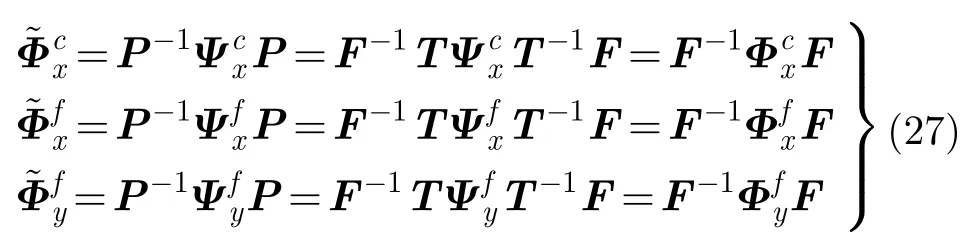
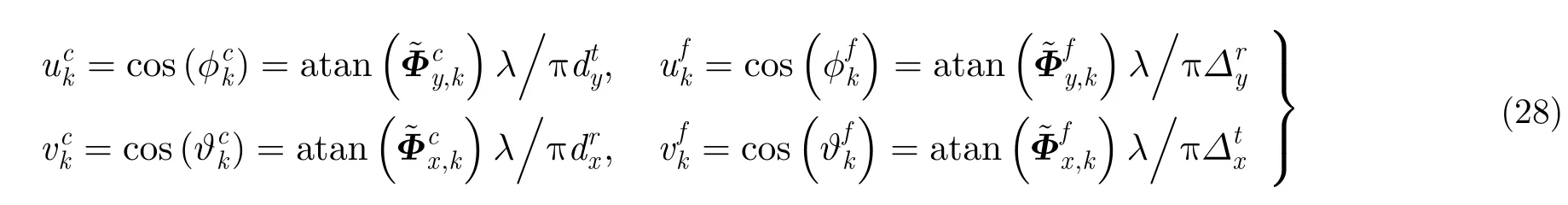
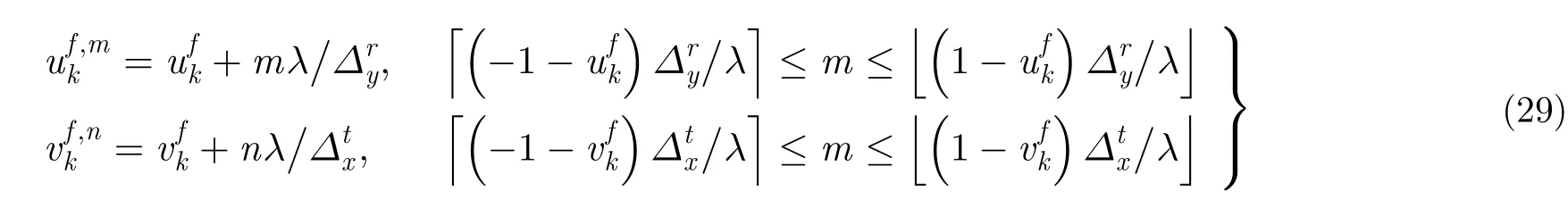
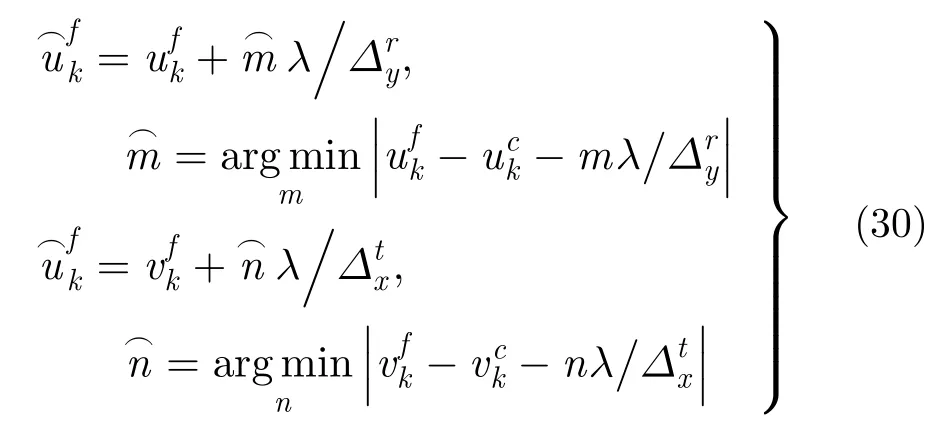
则对应的无模糊高精度2维空间角以及对应的方位、俯仰估计值为：

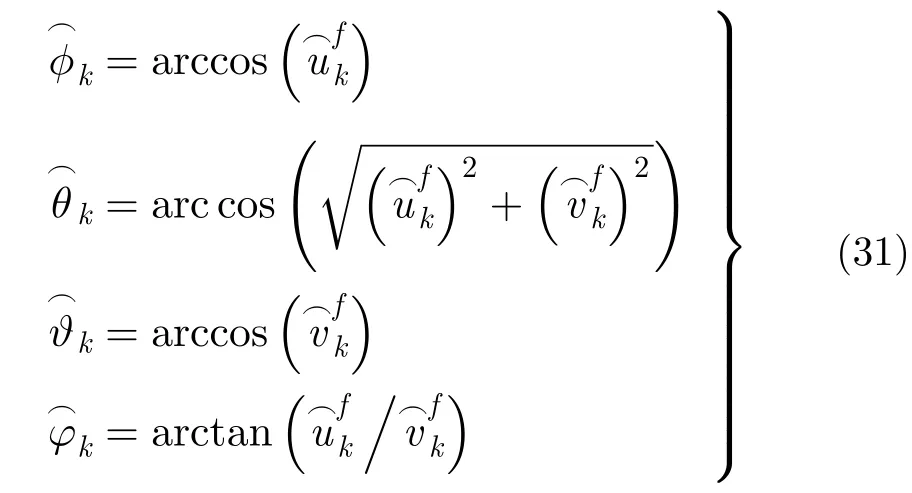
至此，将算法流程总结如下：

（1）利用回波数据计算对应的协方差矩阵，并进一步通过前后向平滑构建相应的Centro-Hermitian矩阵；

（2）根据式（9）构建对应的酉变换矩阵，并进行酉变换处理和特征分解，获得实数域的信号子空间；

（3）根据3.2.1节利用估计的信号子空间，进行实数域粗估计和精估计的联合估计；

（4）根据3.2.2节实现粗估计和精估计间参数的配对，并利用粗估计值来解对应高精度估计的周期性模糊，最终获得无模糊的2维高精度估计。

3.3算法性能及运算复杂度分析

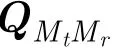
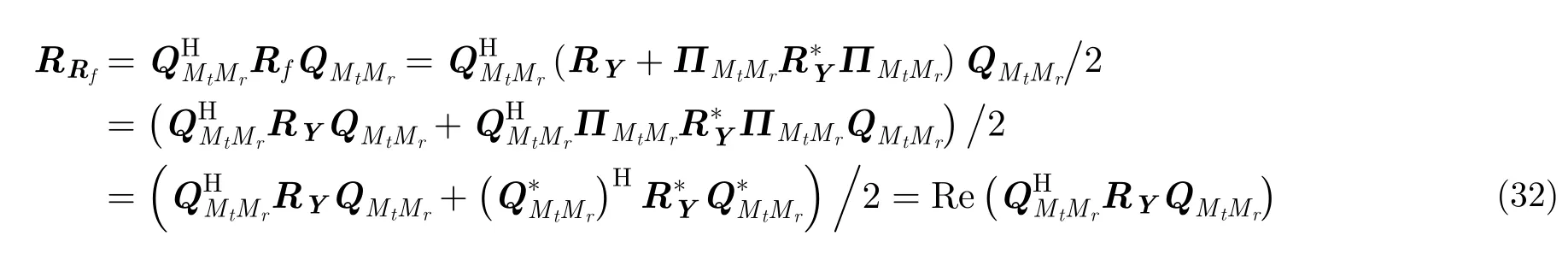
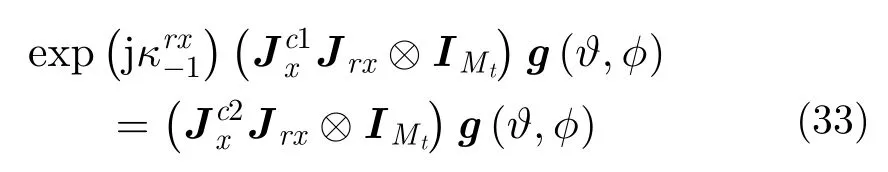
对应的实数域旋转不变性为：

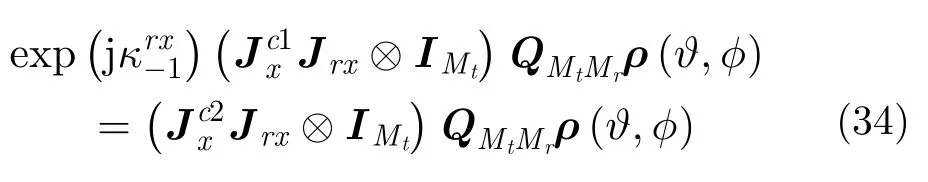
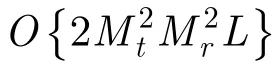
4　仿真实验与数据分析

假设十字型阵列配置下的单基地MIMO雷达，雷达收发阵列结构如图1所示，以Hadamard编码信号为发射波形，分别进行以下仿真实验。

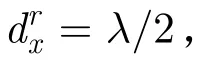
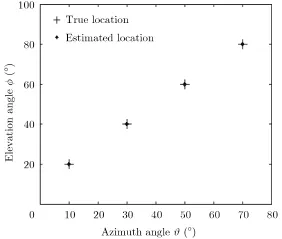
图2　本文算法的估计结果Fig.2　The estimation result of proposed method

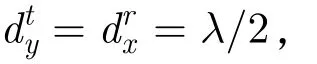
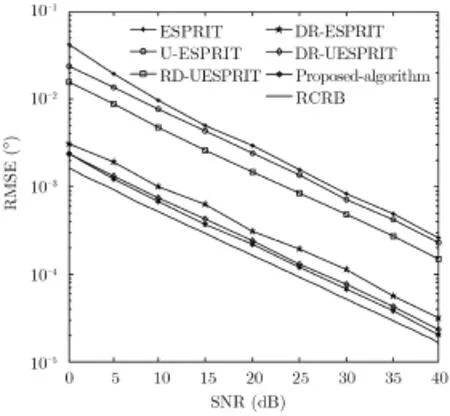
图3　不同算法间空间角估计性能与信噪比的关系Fig.3　Spatial angles estimation performance versus SNR with different methods

由图3仿真结果可以看出，随着信噪比的增大，以上几种算法参数估计的RMSE逐渐变小，估计精度越来越高，这一点很好理解；同时与文献［15，17，18］算法仅利用短基线阵元间距（半波长）进行参数估计相比，本文算法长、短基线相结合的十字型阵列，利用双尺度法进行解周期模糊处理，实现长基线阵元间距的高精度无模糊估计，因此估计精度更优；特别地与文献［13］收发均采用方形阵列相比，本文对应的十字型阵列构型简单，在获得更高估计性能的同时不会造成阵列冗余，能够有效减少收发阵元数目及硬件开销。与DR-ESPRIT算法相比，传统DR-UESPRIT算法以及本文所提算法在利用双尺度进行方位高精度估计时，采用酉变换技术进行实协方差矩阵构造，均复用到了回波数据的共轭，因此对应的信号子空间估计也就更准确，对应的无模糊粗估计和高精度估计性能较优；与传统DR-UESPRIT算法相比，本文算法在估计精度及性能上与之相当，但在算法复杂度上更优，显然本文通过酉变换矩阵的设计，等效于将发射与接收导向矢量分别实数化，因此发射与接收导向矢量在实数化后Kronecker积的关系并没有改变，对应的长、短基线旋转不变特性经过酉变换映射到实数域后并没有改变，有效克服了传统DR-UESPRIT算法中收发流型矢量整体进行酉变换过程时，由于发射或接收矢量非理想造成的实数域流型矢量中待求参量间的耦合问题，因此与DR-UESPRIT算法相比，本文算法能够在保证估计精度的同时，实现回波矩阵特征分解和多参量联合估计求解的全部实数化，算法复杂度更优。

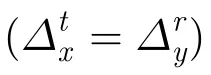
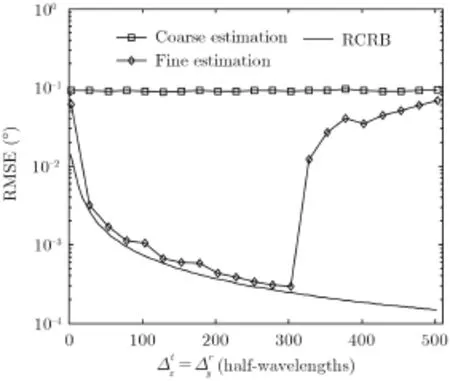
图4　本文算法估计性能与基线长度之间的关系Fig.4　Estimation performance of the proposed method versus long baseline

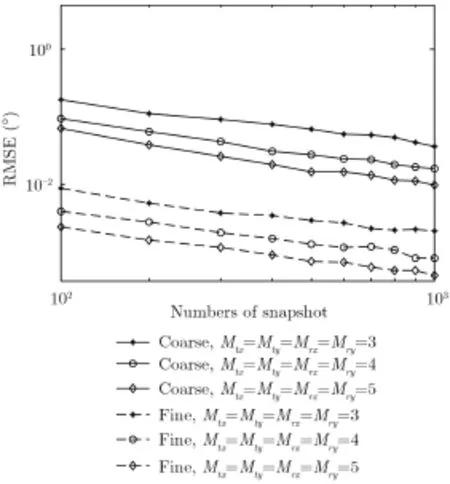
图5　本文算法估计性能与阵元数/快拍数间的关系Fig.5　Estimation performance of the proposed method versus numbers of array/snapshot

5　总结

本文针对单基地MIMO雷达的2维测向问题，提出一种具有2维双尺度平移不变特性的收、发十字型阵列设计，并针对传统DR-UESPRIT算法求解过程中存在的实数域旋转不变因子无法提取的问题，提出一种新的基于酉变换的高精度估计算法，理论分析与仿真结果表明：本文算法不牺牲阵列孔径，在获得2维空间角度无模糊高精度估计的同时，无需额外的配对算法和谱搜索；与传统酉变换过程相比，本文算法的酉变换过程等效将发射与接收导向矢量分别实数化，能够实现特征分解与参数求解完全实数化，具有更低的运算复杂度，更便于实际工程应用。

［1］Huleihel W，Tabrikian J，and Shavit R.Optimal adaptive waveform design for cognitive MIMO radar［J］.IEEE Transactions on Signal Processing，2013，61（20）：5075-5089.

［2］Wang P，Li H B，and Himed B.A parametric moving target detector for distributed MIMO radar in non-homogeneous environment［J］.IEEE Transactions on Signal Processing，2013，61（9）：2282-2294.

［3］Zhang X，Huang Y，Chen C，et al..Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar［J］.IET Radar，Sonar & Navigation，2012，6（8）：796-801.

［4］Zhang X and Xu D.Low-complexity ESPRIT-based DOAestimation for colocated MIMO radar using reduceddimension transformation［J］.Eletronics Letters，2011，47（4）：283-284.

［5］文才，王彤.单基地MIMO雷达降维酉ESPRIT算法［J］.系统工程与电子技术，2014，36（6）：1062-1067.Wen C and Wang T.Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar［J］.Systems Engineering and Electronics，2014，36（6）：1062-1067.

［6］Wang W，Wang X，Song H，et al..Conjugate ESPRIT for DOA estimation in monostatic MIMO radar［J］.Signal Processing，2013，93（7）：2070-2075.

［7］Chen H W，Li X，Jiang W D，et al..MIMO radar sensitivity analysis of antenna position for direction finding［J］.IEEE Transactions on Signal Processing，2012，60（10）：5201-5216.

［8］Chen H W，Zhou W，Yang J，et al..Manifold sensitivity analysis for MIMO radar［J］.IEEE Geoscience and Remote Sensing Letters，2012，9（5）：999-1003.

［9］Chen H W，Yang J，Zhou W，et al..Manifold studies on fundamental limits of direction finding multiple-input multiple-output radar systems［J］.IET Radar，Sonar & Navigation，2012，6（8）：708-718.

［10］Li J F，Zhang X F，Chen W Y，et al..Reduced-dimensional ESPRIT for direction finding in monostatic MIMO radar with double parallel uniform linear arrays［J］.Wireless Personal Communications，2014，77（1）：1-19.

［11］王伟，王晓萌，李欣，等.基于MUSIC算法的L型阵列MIMO雷达降维DOA估计［J］.电子与信息学报，2014，36（8）：1954-1959.Wang Wei，Wang Xiao-meng，Li Xin，et al..Reduceddimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array［J］.Journal of Electronics & Information Technology，2014，36（8）：1954-1959.

［12］梁浩，崔琛，代林，等.基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计［J］.电子与信息学报，2015，37（8）：1928-1935.Liang Hao，Cui Chen，Dai Lin，et al..Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array［J］.Journal of Electronics & Information Technology，2015，37（8）：1928-1935.

［13］Li J F and Zhang X F.Unitary reduced-dimensional estimation of signal parameters via rotational invariance techniques for angle estimation in monostatic multipleinput-multiple-output radar with rectangular aarrays［J］.IET Radar，Sonar & Navigation，2014，8（6）：575-584.

［14］Zheng G M and Chen B X.Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar［J］.Multidmensional Systems and Signal Processing，2015，26（1）：159-178.

［15］Zheng G M，Chen B X，and Yang M L.Unitary ESPRIT algorithm for bistatic MIMO radar［J］.Electronics Letters，2012，48（3）：179-181.

［16］Ren S，Ma X，Yan S，et al..2-D unitary ESPRIT-like Direction-Of-Arrival（DOA）estimation for coherent signals with a uniform rectangular array［J］.Sensors，2013，13（4）：4272-4288.

［17］Chen D F，Chen B X，and Guo D Q.Angle estimation using ESPRIT in MIMO radar［J］.Electronics Letters，2008，44（12）：770-771.

［18］Chen J L，Gu H，and Su W M.Angle estimation using ESPRIT without pairing in MIMO radar［J］.Electronics Letters，2008，44（24）：1422-1423.

［19］Lemma A N，Veen A J，and Deprettere E F.Multiresolution ESPRIT algorithm［J］.IEEE Transactions on Signal Processing，1999，47（6）：1722-1726.

梁 浩（1987-），男，博士研究生，主要研究方向为阵列信号处理以及 MIMO雷达信号处理。

E-mail：lhmailhappy@163.com

崔 琛（1962-），男，教授，博士生导师，主要研究方向为雷达信号处理。

E-mail：kycuichen@163.com

余 剑（1980-），男，讲师，硕士，主要研究方向为雷达信号处理以及雷达对抗技术。

E-mail：jimmyyu1112@hotmail.com

Two-dimensional DOA Estimation with High Accuracy for MIMO Radar Using Cross Array

Liang HaoCui ChenYu Jian
（401 Laboratory，Department of Communication Countermeasure，Electronic Engineering Institute，Hefei 230037，China）

In this study，we investigate the estimation of the Two-Dimensional（2D）Direction Of Arrival（DOA）in monostatic multiple-input-multiple-output radar with cross array and propose a novel，highly accurate DOA estimation method based on unitary transformation.First，we design a new unitary matrix using the central symmetry of a cross array at transmit and receive sites.Then，the rotational invariance relationships of these arrays with long and short baselines can be transformed into a real-value field via unitary transformation.In addition，non-ambiguous and highly accurate 2D DOA estimations can be obtained using a unitary dual-resolution ESPRIT algorithm.Simulations show that the proposed method can estimate 2D highly accurate spatial angles using automatic pairing without incurring the expense of array aperture and peak searching.Compared with traditional unitary transformation，the steering vectors of transmit and receive arrays can be transformed into real-value fields via the unitary matrix and the transformation method of our scheme，respectively.This effectively overcomes the problem of shift invariance factors in real-value fields that cannot be extracted using traditional algorithms.Therefore，the proposed method can absolutely computeeigenvalue decomposition and estimate parameters in a real-value field，resulting in lower computational complexity compared with traditional methods.Simulation results verify both the correctness of our theoretical analysis and the effectiveness of the proposed algorithm.

MIMO radar； Cross array； Unitary transformation； Dual-resolution unitary ESPRIT

TN957.51

A

2095-283X（2016）03-0254-11

10.12000/JR16016

2016-01-21；改回日期：2016-03-29；网络出版：2016-05-20

梁浩 lhmailhappy@163.com

国家自然科学基金（60702015），安徽省科技攻关项目（1310115188），电子工程学院院控科研基金（KY13A197，KY13A200，KY13A206）

Foundation Items：The National Natural Science Foundation of China（60702015），Anhui Province Foundation for Science and Technology Research Project（1310115188），Scientific Research Foundation of Electronic Engineering Institute（KY13A197，KY13A200，KY13A206）