夹层板脱层对结构振动特性的影响分析

陈一鸣，田阿利，尹　群，叶仁传（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

夹层板脱层对结构振动特性的影响分析

陈一鸣，田阿利，尹群，叶仁传
（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

聚氨酯弹性体钢夹层板结构（SPS）因其优异的力学性能和可设计性，近年来在船舶制造等领域得到广泛应用。本文通过理论与数值仿真，研究了SPS 夹层板结构自由振动以及脱层对振动特性的影响。首先，对 SPS夹层结构，提出一种等效模型，采用简化一阶剪切变形理论，建立了夹层板横向自由振动控制方程，并结合边界条件给出了SPS 夹层结构的振动频率表达式。通过与文献和数值仿真结果的对比分析，验证了本模型与方法的有效性与准确性。考虑结构易脱层的特点，研究了面/芯脱层对结构振动特性的影响，对比分析脱层范围、脱层位置以及脱层形状对结构低阶频率的影响，给出了各脱层参数与结构低阶振动频率的关系，为 SPS 结构的设计与应用提供指导。

夹层板；自由振动；面/芯脱层；有限元分析

0　引 言

作为一种造船新型材料，夹芯板体系（Sandwich Plate System，SPS）由全球最大的化工公司——德国巴斯夫和英国 IE 公司共同推出，是一种具有高比强度、高比刚度、性能可设计等优点的新型复合材料，同时夹芯板具有很好的缓冲作用，可作为耐撞结构应用于船舶结构设计，提高其耐撞性能［1-2］。SPS 因力学性能好、造船成本低、修船方便等优势而被广泛应用于船舶的建造与修理中。2010年，SPS 在 150 余艘船舶的修理面积达 80 000 余平方米。SPS 技术有望给国内船舶工程领域的维修带来可观的经济效益，引领造船工业新时代。

SPS 结构是两层钢板用聚氨酯弹性体混合物填充剂紧紧粘合在一起而成的夹层结构，其力学性能的研究，最早的主要有 Reissner 理论、Hoff 理论和杜庆华理论。文献［3］在总结上述 3 种理论基础上，详细分析了各种力学因素的作用，从理论上给出了多种边界条件及载荷作用下各向同性、各向异性夹层板弯曲、稳定和自由振动的解析解。在 3 种理论基础上，学者们又相继提出一些模型理论，近年来仍在逐步完善。Lee［4］建立了一种考虑芯板横向压缩变形影响的夹层板弯曲振动模型，但仍遵守直法线假定。王海英［5］建立了一种考虑面板基于一阶剪切变形理论，芯板基于后板非线性变形理论夹层板动力特性的有限元模型。王盛春等［6］以四边简支正交各向异性蜂窝夹层板为研究对象，应用 Reissner-Mindlin 夹层板剪切理论，给出一种将夹层板弯曲控制方程组化为仅含一个位移函数的单一方程的方法。

由于夹层板的结构特点，聚合物浇铸时，因流速的控制等因素会在面板和芯材之间形成气泡，形成粘连不完全。且这种结构在抗冲击载荷时，易在粘连处产生脱层损伤。因此，研究脱层对 SPS 结构的力学特性，对该结构在船体上的广泛应用具有重要的意义，也成为近些年夹层板应用研究的一个热点问题。

白瑞祥等［7-8］对含面/芯开裂损伤复合材料夹层板的动力特性进行了较为系统的研究。张文志等［9］对层合梁结构的脱层问题，提出了一种半解析模型和相应的精细积分方法。Aviles F 等［10］对含脱层损伤夹层板的局部屈曲进行了研究。V.N.Burlayenko 等［11-12］运用有限元软件 Abquas 分析了夹层板局部脱层下的自由振动和外载荷下的动态响应。Lou J［13］采用试验和数值仿真的方法对含局部损伤的锥体桁架夹芯板的振动特性进行参数化研究。

本文以船用 SPS 夹层板为对象，采用理论与数值方法主要研究 SPS 结构的振动特性及脱层对结构振动特性的影响。首先，采用一种简化的一阶剪切变形理论，将夹层板看作为各向同性板，将弯曲振动控制方程组化为一个只含有横向位移函数的方程，对 SPS 夹层板结构的振动特性进行理论研究，并编程实现。计算结果与经典理论对比分析，验证本文方法的准确性。同时，考虑 SPS 结构易脱层的特点，采用有限元方法分析面/芯脱层对 SPS 夹层板振动特性的影响，主要分析脱层面积、脱层位置以及脱层形状等因素的影响，并建立了主要影响参数与结构低阶振动频率之间的关系。

1　基本理论与分析模型

1.1基本假设和控制方程

SPS 夹层板结构，由上面板、聚氨酯弹性体芯层和下面板粘合而成，如图1所示。根据 Reissenr-Mindlin的夹层板理论和夹芯的“反平面”理论，基本假设为：

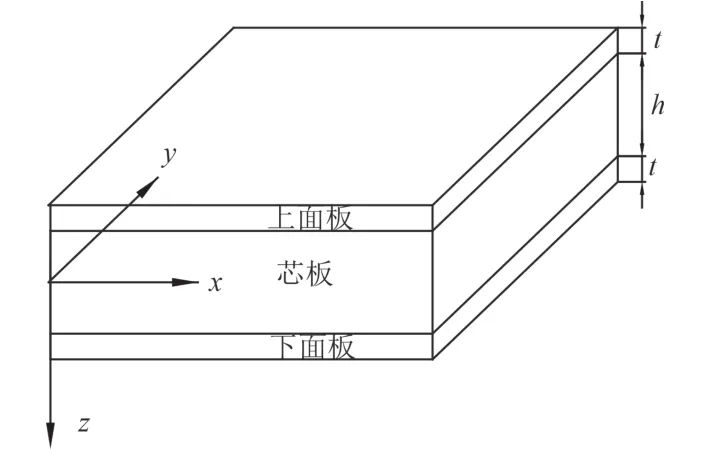
图1　夹层板示意图和符号系统Fig.1　Schematic of sandwich plate and corresponding coordinate system

1）面板厚度很小，可作薄膜处理；

2）原垂直于中面的法线受载后长度不变，应变为0，即 εz=0；

3）考虑横向剪切变形的影响，将横向位移分为由弯曲和剪切两部分位移组成，即 w=wb+ ws。

由于 SPS 夹层板芯材材质较软，厚度较大，如采用 Kirchhoff 薄板理论将产生较大误差，所以对于夹层板而言，考虑剪切效应十分必要。本文为简化计算，提出了一种等效简化模型，即将夹层板等效为具有相同刚度的各向同性板。等效板的弯曲刚度为：

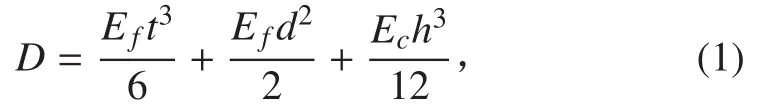
式中：Ef为面板弹性模量；Ec为芯层弹性模量；d为上、下面板中性轴的距离。等效板的剪切刚度为：

式中 Gc为芯层剪切模量。

板的一阶剪切变形理论位移模式为：

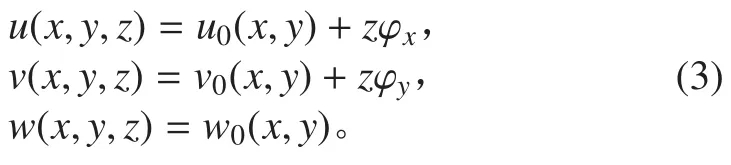
式中：u0，v0，w0，φx和 φy为板中面的位移函数；z为任意点距中面的距离。

本文采用简化的一阶剪切变形理论［14］，将整体横向位移分为弯曲和剪切两部分，即 w=wb+ ws，其中wb为由弯曲引起的位移，ws为由剪切引起的位移；令φx=-∂wb/∂x，φy=-∂wb/∂y，则夹层板内任意一点的位移 u，v，w 可表示为：

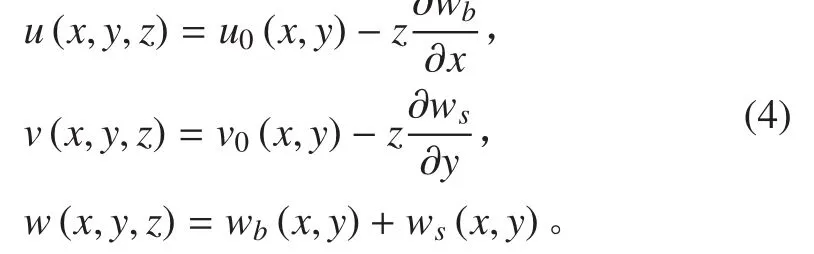
现在式（4）中就仅含4个未知数（u，v，wb，ws），由几何方程得夹层板应变场为：

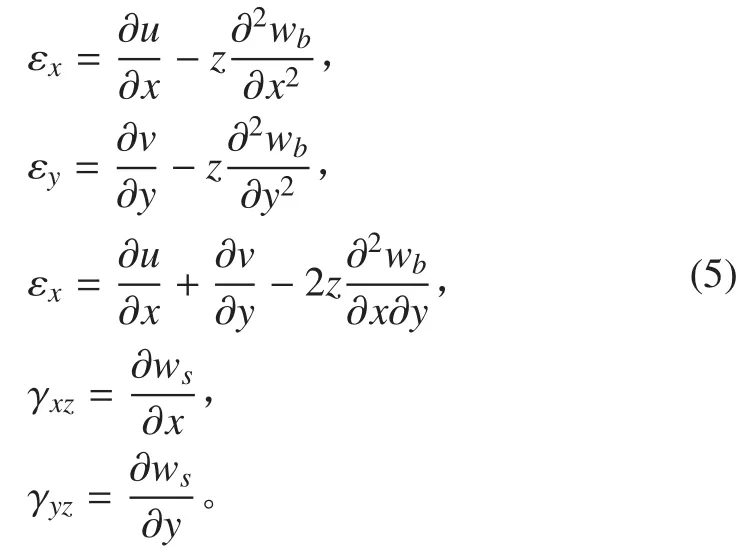
内力与位移的关系式为：

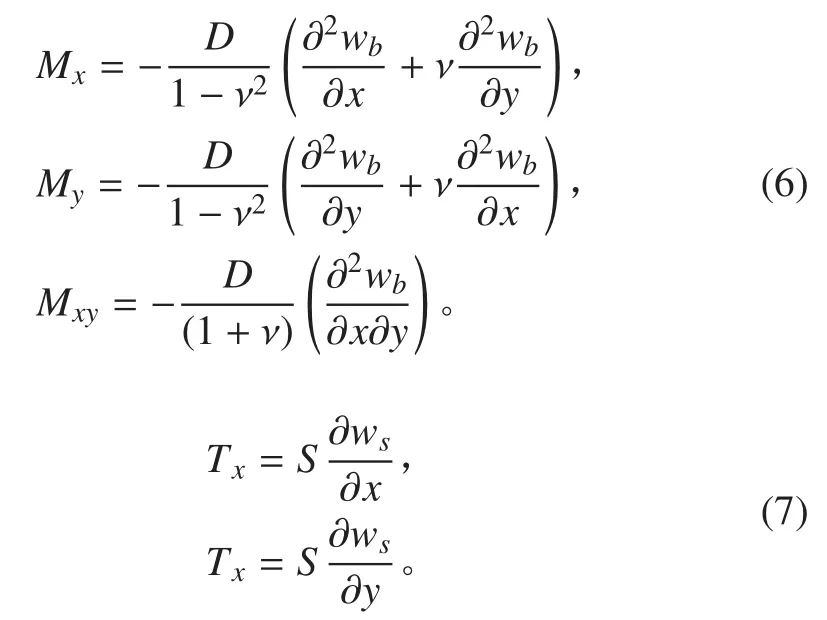
忽略面内惯性力，平衡方程为：

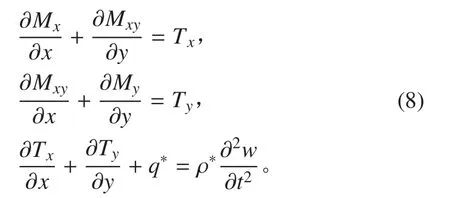
将式（5）、式（6）代入式（7），得到夹层板横向自由振动控制方程：

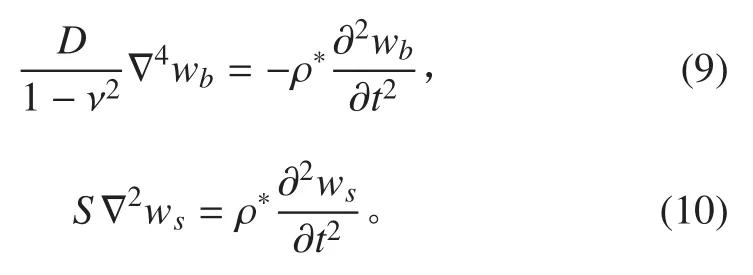
整理成仅含一个整体横向位移的控制方程为：

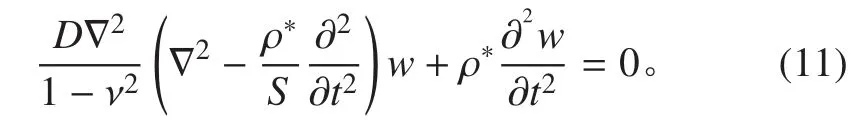
式中：Mx，My和 Mxy为夹层板内力矩；Tx，Ty为夹层板的横向剪切力。

1.2四边简支夹层板的边界条件与求解

四边简支的夹层板边界条件为：

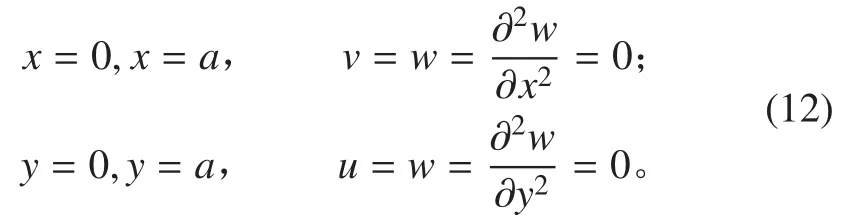
采用分离变量法求解，自由振动的挠度可设为：

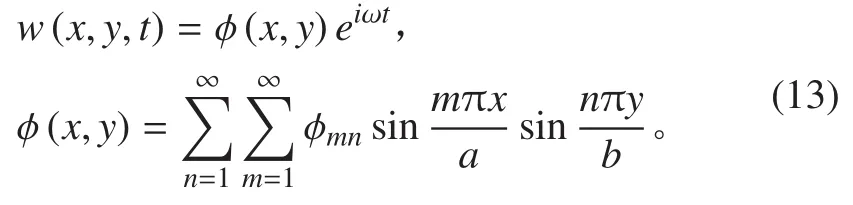
将式（13）代入控制方程（11），计算可得四边简支夹层板结构的固有频率计算公式为：

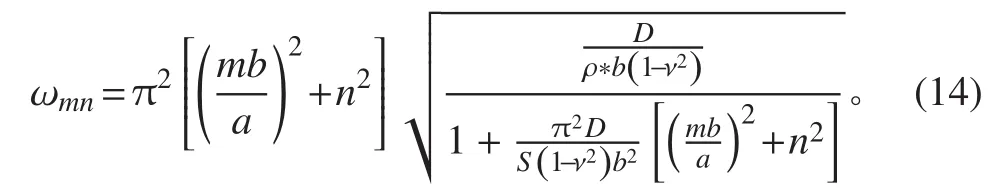
2　结果验证与分析

四边简支 SPS 结构模型如图2所示，为便于比较，以文献［3］中的经典解析方法算例为比较对象。该结构边长为 a=b=500mm，上下面板厚度均为 t=2mm，芯材厚度h=15mm。其中，面板弹性模量 Ef=18 GPa，密度 ρf=800kg/m3，泊松比 v=0.3；芯材弹性模量 Ec=0.18 GPa，密度 ρc=117.5kg/m3，泊松比 v=0.3。

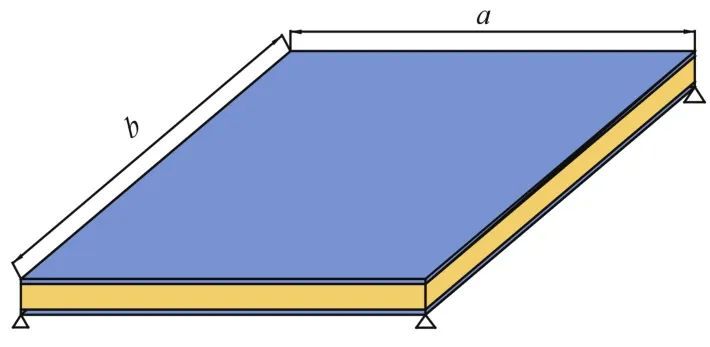
图2　四边简支方形夹层板结构示意图Fig.2　Schematic of simply supported sandwich plate

通过本文等效简化方法，计算得到结构的固有频率，并与文献［3］提供的经典解析结果及有限元方法（Ansys/Workbench）计算结果进行比较，如表1所示，模态振型如图3所示。

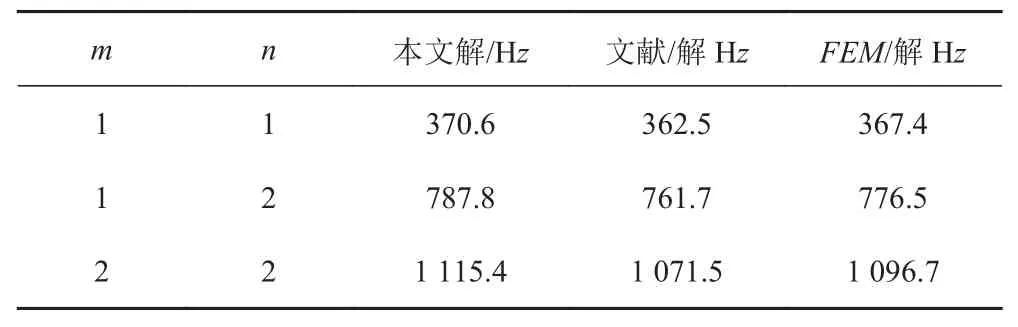
表1　夹层板固有频率比较Tab.1 Natural frequencies of the sandwich plate

由表1可看出，本文通过等效简化模型计算分析四边简支 SPS 结构的固有频率，与文献［3］中的经典解析方法得到的结果，以及有限元计算结果均吻合较好，误差很小，因此，在满足工程精度要求的基础上，本文提出的等效简化方法分析夹层板振动特性，不仅有效而且更为简便。

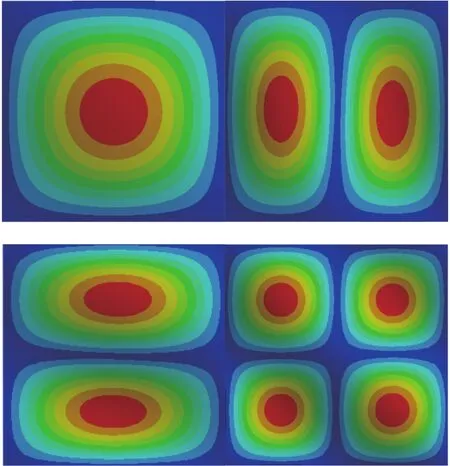
图3　简支夹层板模态振型图Fig.3　Modal shapes of simply supported sandwich plate

3　面/芯脱层损伤对 SPS 振动特性的影响

考虑 SPS 加工过程中的缺陷以及承载后发生的脱层问题，研究面/芯脱层损伤对结构振动特性的影响，主要分析脱层的大小、位置以及形状参数对结果的影响。

3.1脱层范围对固有频率的影响

选择一典型船用SPS结构，边长 a=1m，上、下面板厚度均为 t=9mm，聚氨酯芯材厚度h=40mm。其中，面板材料为低碳钢，弹性模量 Ef=206 GPa，密度 ρf=7 850kg/m3，泊松比 v=0.3；聚氨酯弹性体芯材弹性模量 Ec=1.419 GPa，密度 ρc=1 200kg/m3，泊松比 v=0.476。

结构脱层区域通常发生在层间应力最大的地方。对于四边简支板，设在夹层板中心处有一圆形脱层区域。含面/芯脱层损伤有限元模型图与局部示意图分别如图4所示。

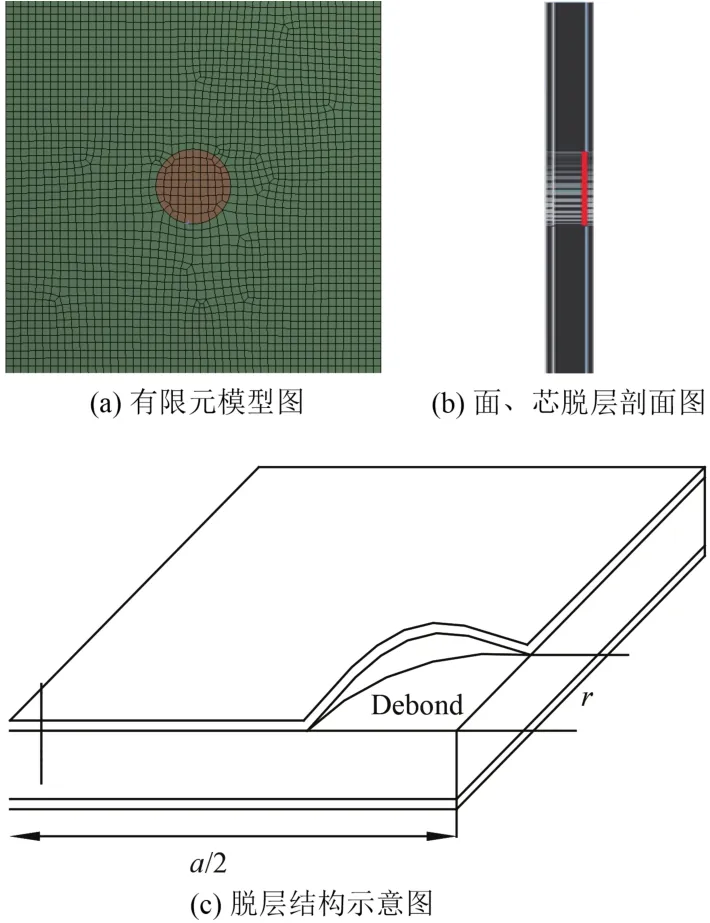
图4　含面芯脱层夹层板示意图Fig.4　Schematic diagram of sandwich with facecore interface debonding

图5给出了夹层板固有频率随脱层区域半径 r的关系。从图中曲线可看出，对于 SPS 夹层板，面/芯脱层损伤对夹层板固有频率有很大影响。影响大致可分以下 3个阶段：

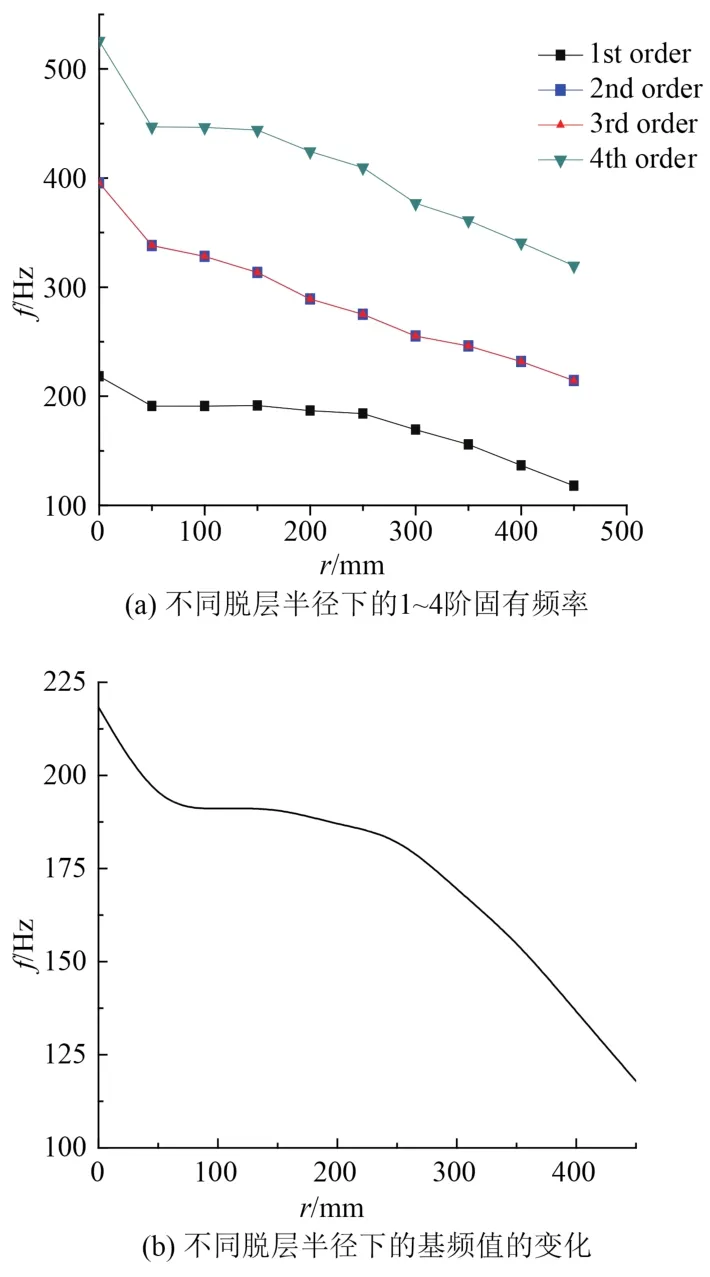
图5　不同脱层半径下的基频变化Fig.5　Frequencies under different debonding district radius

1）始发阶段，即脱层发生到逐渐扩大过程，此时，脱层区域较小，但 SPS 夹层板结构的低阶频率变化显著，随脱层区域增大而快速降低；

2）结构频率较稳定阶段，即在此阶段，随脱层面积的增大，结构低阶频率变化较小；

3）结构低阶频率再次进入快速变化，脱层范围大约超过整体结构的一半时，随着脱层区域增大，结构基频也快速降低。

3.2脱层位置对夹层板固有频率的影响

在实际中，因加工等问题，面/芯脱层可能发生在夹层板的任何位置。选取稳定阶段的脱层半径，以 r=100mm为例，比较分析脱层位置对结构振动特性的影响。因结构对称，以1/4为分析对象，任意选取脱层位置，本文选取典型的4个位置 P（x，y）进行比较：P1（150，500），P2（200，500），P3（250，500），P4（200，200）。

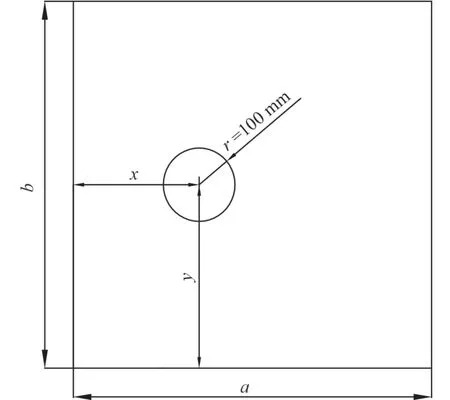
图6　圆形损伤位置示意图Fig.6　Schematic diagram of the position of debonding area

由图7可以看出，相同结构，相同的面/芯脱层条件下，脱层发生的位置对 SPS 结构的低阶振动频率影响非常微弱。

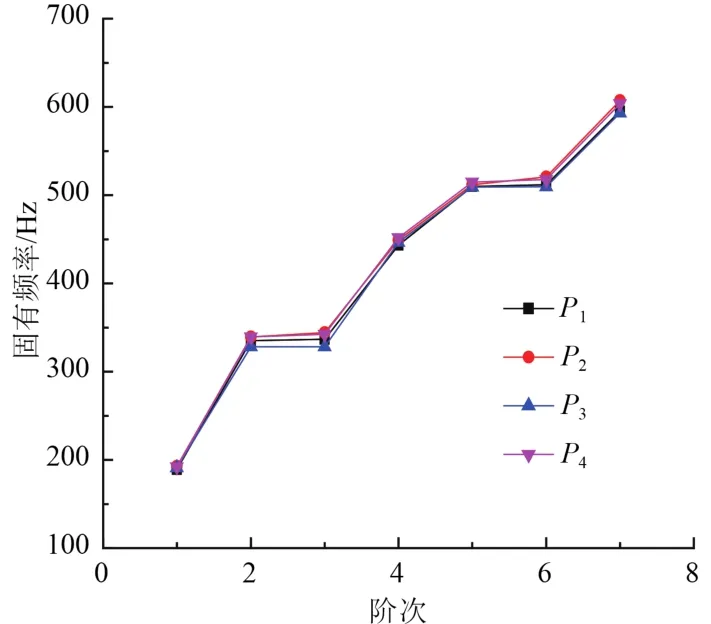
图7　脱层位置不同时夹层板的固有频率Fig.7　Frequencies under different position of debonding

3.3脱层形状对夹层板固有频率的影响

设在正方形夹层板中心有一椭圆形损伤区域，长轴长度为 a，短轴长度为 b。表2给出了椭圆形脱层区域和具有相同面积的圆形脱层对结构固有频率的影响对比结果。从表中可看出，脱层区域形状对固有频率有一定影响。相同面积情况下，椭圆形脱层的低阶频率均高于圆形脱层的频率；而且随着椭圆形的长短轴之比值越大，SPS 结构振动低阶频率越高。

表2　不同脱层形状的结构频率Tab.2 Frequencies with different debonding shape

4　结 语

本文提出了一种简化等效的方法计算四边简支SPS 夹层板的自由振动问题，并基于此，对比研究了含面芯脱层的夹层板结构的振动特性，重点分析了脱层范围、脱层位置以及脱层形状对 SPS 结构固有频率的影响，为 SPS 结构在船体上的应用，提供指导。文中主要结论如下：

1）针对 SPS 结构提出的简化等效方法，能够计算结构自由振动问题，通过与经典解析以及有限元方法结果比较，吻合较好，验证了本文方法的合理与有效性，且具有很好的精度。

2）脱层区域的大小对夹层板振动特性具有显著影响。通过大量计算，脱层大小对结构低阶频率的影响可分为即始发阶段、稳定阶段和快速变化阶段 3个阶段。随着脱层范围的增大，对 SPS 结构的振动影响经历上述阶段。

3）相同脱层发生在结构不同位置时，对结构低阶频率影响微弱，可忽略。

4）在相同面积脱层区域前提下，不同脱层形状，对夹层板固有频率有影响。椭圆形脱层的结构固有频率高于圆形，且脱层面积不变时，椭圆形长短轴之比越大，结构低阶振动频率越高。

［1］周红，张延昌，岳亚霖.夹层板系统碰撞性能数值仿真分析［J］.舰船科学技术，2014，36（1）：84-90.ZHOU Hong，ZHANG Yan-chang，YUE Ya-lin.Numerical simulation analysis for sandwich plate system under collision load［J］.Ship Science and Technology，2014，36（1）：84-90.

［2］王自力，张延昌，顾金兰.基于夹层板抗水下爆炸舰船底部结构设计［J］.舰船科学技术，2010，32（1）：22-27.WANG Zi-li，ZHANG Yan-chang，GU Jin-lan.Anti-s-shock double bottom structure design of warship based on sandwich panel［J］.Ship Science and Technology，2010，32（1）：22-27.

［3］中国科学院北京力学研究所固体力学研究室板壳组.夹层板壳的弯曲、稳定和振动［M］.北京：科学出版社，1977.

［4］LEE L J，FAN Y J.Bending and vibration analysis of composite sandwich plates［J］.Computers & Structures，1996，60（1）：103-112.

［5］王盛春，邓兆祥，沈卫东，等.四边简支条件下正交各向异性蜂窝夹层板的固有特性分析［J］.振动与冲击，2012，31（9）：73-77，89.WANG Sheng-chun，DENG Zhao-xiang，SHEN Wei-dong，et al.Connatural characteristics analysis of rectangular orthotropic honeycomb sandwich panels with all edges simply supported［J］.Journal of Vibration and Shock，2012，31（9）：73-77，89.

［6］王海英，赵德有.芯板横向可压缩位移模式的夹层板结构动力有限元分析［J］.船舶力学，2009，13（5）：795-802.WANG Hai-ying，ZHAO De-you.Finite element analysis for sandwich plates with moderately thick viscoelastic cores［J］.Journal of Ship Mechanics，2009，13（5）：795-802.

［7］白瑞祥，陈浩然.含界面脱粘及表板基体开裂损伤的复合材料夹层板非线性稳定性的研究［J］.复合材料学报，2002，19（2）：80-84.BAI Rui-xiang，CHEN Hao-ran.Investigation of nonlinear buckling behavior of composite sandwich plates with interfacial delamination and matrix micro-cracks［J］.Acta Materiae Compositae Sinica，2002，19（2）：80-84.

［8］白瑞祥，王蔓，陈浩然.具有分层损伤的不同加筋形式复合材料层合板的后屈曲性态研究［J］.计算力学学报，2006，23（2）：186-190.BAI Rui-xiang，WANG Man，CHEN Hao-ran.Study on postbuckling behavior of delaminated composite plastes with different stiffeners［J］.Chinese Journal of Cmputational Mechanics，2006，23（2）：186-190.

［9］张文志，富明慧，林敬华.层合梁脱层分析的精细解法［J］.工程力学，2012，29（7）：35-41.ZHANG Wen-zhi，FU Ming-hui，LIN Jing-hua.A precise method for delamination analysis on laminated composite beams［J］.Engineering Mechanics，2012，29（7）：35-41.

［10］AVILÉS F，CARLSSON L A.Elastic foundation analysis of local face buckling in debonded sandwich columns［J］.Mechanics of Materials，2005，37（10）：1026-1034.

［11］BURLAYENKO V N，SADOWSKI T.Finite element nonlinear dynamic analysis of sandwich plates with partially detached facesheet and core［J］.Finite Elements in Analysis and Design，2012，62：49-64.

［12］BURLAYENKO V N，SADOWSKI T.Nonlinear dynamic analysis of harmonically excited debonded sandwich plates using finite element modelling［J］.Composite Structures，2014，108：354-366.

［13］LOU J，WU L Z，MA L，et al.Effects of local damage on vibration characteristics of composite pyramidal truss core sandwich structure［J］.Composites part b：Engineering，2014，62：73-87.

［14］SHENOI R A，GROVES A，RAJAPAKSE Y D S.Theory and applications of sandwich structures［M］.Southampton，UK：University of Southampton，2005.

Effect analysis of delamination for vibration characteristic of sandwich plate

CHEN Yi-ming，TIAN A-li，Yin Qun，YE Ren-chuan
（School of Naval Architecture and Ocean Engineering，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

Steel-polyurethane-steel （SPS）plate has got an extensive application in engineering such as the ship building and civil bridge due to the excellent mechanical properties and designability.The present paper investigated the vibration characteristic of SPS plate and the effect of face/core delamination based on the analysis and simulation methods.Firstly，a mechanical equivalent model of SPS was proposed to reduce the governing equations of SPS vibration with a simplified firstorder shear deformation theory.The analysis formula natural frequencies of SPS with simple supported boundary conditions were obtained.Then，the validity and accuracy of the present method were verified via comparison of results in literature and finite element method.Considering this kind of sandwich plate is easy to occur face/core delamination，the effects of delamination on the structure vibration characteristic were studied from the aspects of delamination areas，locations and shape.The results in present paper look forward to provide guidance for the design and application of SPS structure.

sandwich plate；free vibration；face/core delamination；finite element analysis

U661.44； O327

A

1672-7619（2016）07-0011-05

10.3404/j.issn.1672-7619.2016.07.003

2015-10-10；

2015-12-15

国家自然科学基金青年基金资助项目（E091002/51109101）

陈一鸣（1990-），男，硕士研究生，主要从事船舶结构力学性能研究。