导管式推进器非定常性能数值计算方法研究
2016-10-09舒礼伟海军装备部北京100841
舒礼伟(海军装备部,北京 100841)
导管式推进器非定常性能数值计算方法研究
舒礼伟
(海军装备部,北京 100841)
基于滑移网格方法,采用SST k-ω 湍流模型研究不同网格划分方式对带前置定子导管式推进器非定常性能的研究。首先基于相对参考坐标系法及滑移网格方法分别对推进器在定常与非定常下的性能进行数值预报,并与试验结果相比验证计算方法的可靠性。基于该方法研究整体网格划分方式与周期性网格对推力系数、扭矩系数与推进器各个方向上的非定常脉动力的影响。研究结果为进一步研究推进器非定常性能提供了参考。
滑移网格;推进器;周期性网格;非定常力
0 引 言
工作在艇后的推进器会产生周期性脉动的非定常力,周期性脉动非定常力是激发推进器线谱噪声的噪声源,它的预报和分析是优化推进器噪声性能的前提,同时也是预报推进器线谱噪声的基础。对推进器非定常力进行数值预报要求能够较为准确地捕捉到推进器较大的推力总量和微小的脉动量,目前已经能较为准确地对推进器定常下的性能分析,对推力值的数值分析精度已能满足工程需求[1],但是微小的推力脉动量的准确捕捉相对较困难,该方面的研究也相对较少。
随着 CFD 技术的快速发展,近年来许多学者致力于研究螺旋桨非定常性能数值计算方法。谭廷寿和熊鹰等[2-3]采用速度势面元法对螺旋桨非定常性能进行了数值预报,通过与试验值的对比验证了计算方法的可靠性。胡小菲等[4]采用滑移网格方法对孤立螺旋桨在给定的非均匀伴流场下的非定常力进行数值分析,研究了整体网格尺度对非定常结果的影响,沈海龙和姚震球等[5-6]将螺旋桨与船体作为一个整体,基于滑移网格方法研究了螺旋桨与船体之间的非定常干扰特性,结果表明船体对螺旋桨的影响主要是尾流场的非均匀性改变了螺旋桨的进流速度,螺旋桨对船体的影响主要是改变了船体表明的压力分布。
工作于艇后的推进器与螺旋桨工作环境类似,但是推进器模型与螺旋桨有所差别,推进器模型由导管、前置定子及转子等组成,非定常性能也将发生变化,目前对推进器非定常性能的研究很少。本文基于SST k-ω 湍流模型,采用滑移网格方法导管式推进器模型的非定常力数值计算方法,并对不同网格划分方式对推进器非定常性能的影响进行研究。
1 计算方法
1.1计算模型与网格
计算模型采用文献[7]中 Hughes 设计的带前置定子的导管式推进器,定子采用 NACA 63-018 翼型,叶片数为 9,转子翼型采用 NACA a=0.8(mod),叶片数为 4,z 轴指向出口,计算模型及坐标系设置如图1所示。整个流场计算域为圆柱体,入口距螺旋桨盘面位置约 6 倍螺旋桨直径,以保证来流速度到达时均匀,出口距螺旋桨盘面位置约 7 倍螺旋桨直径,以保证尾流充分发展,圆柱体直径约为 4 倍螺旋桨直径,以保证计算结果不受边界的影响。
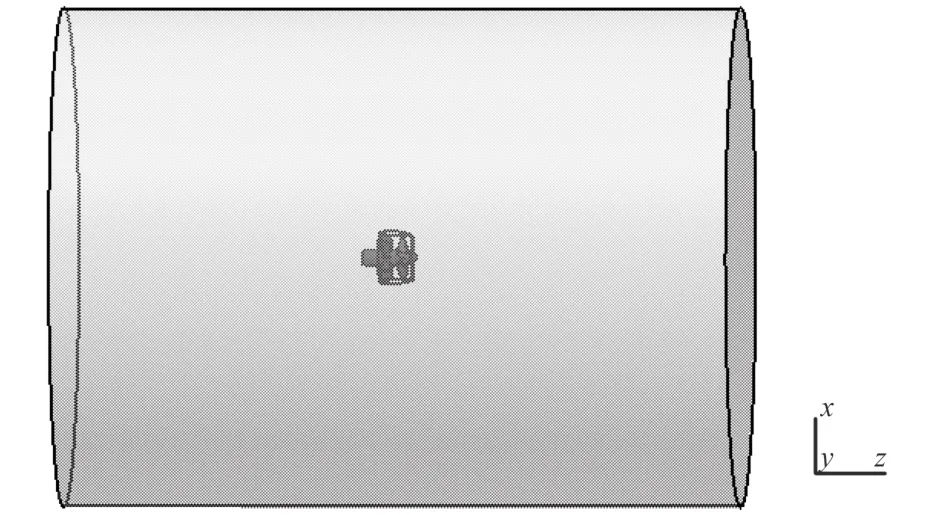
图1 计算模型及坐标系Fig.1 Computational model and coordinate system
整个计算域分为转子域及定子域。整个计算域采用了非结构化网格。转子域与定子域通过 interface 面连接。为了控制转子域附近的网格尺寸,采用 Gambit中的“尺度函数”对转子叶片表面进行加密,尤其是对叶片梢部及导边进行了加密。
1.2计算方法与边界条件
泵喷推进器在艇后非均匀流场中以一定的转速绕轴旋转,属于非定常流动问题。推进器性能分析可采用的数值计算方法有相对参考坐标系、动网格及滑移网格法。相对坐标参考系只适用于推进器的定常流动模拟;动网格方法可进行推进器的非定常数值计算,但在计算过程中需要对网格进行重构,较容易在计算中出现负体积,对网格质量要求高,计算量大,对计算机硬件的要求也更高,所以目前较少使用;目前比较常采用滑移网格方法模拟推进器的非定常性能。
基于 SST k-ω 湍流模型,本文首先采用相对参考坐标系法对泵喷推进器的定常性能进行数值计算,待定常计算充分收敛后且计算精度较高的情况下,以定常计算结果作为初始条件采用滑移网格方法对其非定常性能进行数值分析。计算时的边界条件为:入口采用速度入口,给定来流速度,本文仅研究均匀来流下的非定常性能。出口采用为压力出口。对流项离散格式为二阶迎风格式,耗散项离散格式为二阶中心差分格式。非定常计算中时间离散格式选用二阶隐式格式。为保证残差收敛精度达到 10-4,提高计算精度,压力松弛因子取为 0.15,动量矩松弛因子 0.3,其余采用默认设置。
非定常计算时的时间步长 t 按照每个时间步内推进器旋转 2° 进行设置,即n为推进器转速(r/s)。
1.3数据处理
对导管式推进器进行定常与非定常计算稳定后,可根据式(1)~式(3)得到表征推进器性能的无因次系数,即推力系数与转矩系数
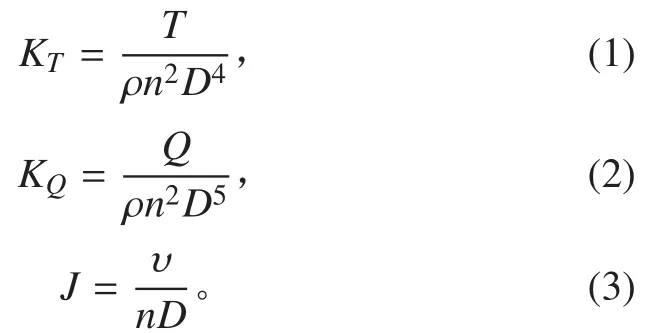
式中:T和 Q为推进器推力与扭矩;J为进速系数;υ为入口速度;n和 D为推进器转速与转子直径;ρ为水的密度。
在采用 Fluent 对推进器进行非定常计算中,将推进器产生的推力按照每个时间步长 t 保存 1次,得到推力值随时间变化的时域图。然后对其进行傅里叶变换可得到推力值在叶频处的脉动力再根据式(4)可得到一阶叶频非定常力下的线谱噪声级
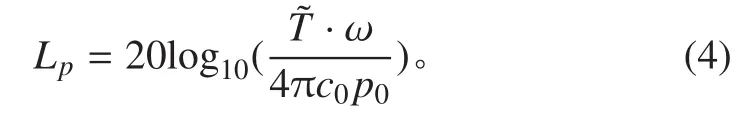
由式(4)可知,为保证线谱噪声预报达到 1dB的水平,非定常力的数值预报误差不能大于 12%。
2 非定常计算结果分析
2.1计算方法验证
采用相对参考坐标系方法与滑移网格方法分别对导管式推进器在进速系数分别为 0.6,0.8,1.0 下进行定常与非定常的计算。定常计算结果如表1所示,试验数据来自于参考文献[7]。进速系数为 0.6 与 0.8 时,数值计算误差均在 5%以下;进速系数为 1.0 时,计算误差有所增加,最大为 6.27%。
以定常计算结果为初始条件对 J=0.6 下导管式推进器采用滑移网格方法进行非定常计算,取时域上的平均值计算与结果如表2所示。非定常计算结果与试验值相比,推力系数与扭矩系数误差均在 10%以下,与定常计算结果相比,推力系数计算精度稍低,但精度已能满足要求,扭矩系数精度得到提高。
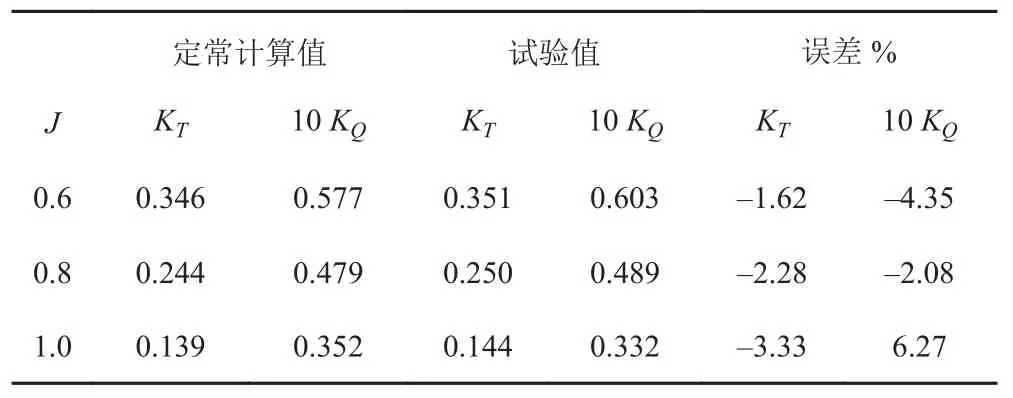
表1 定常计算结果Tab.1 Steady numerical results

表2 非定常计算结果Tab.2 Unsteady numerical results
2.2计算网格影响与结果分析
在研究推进器非定常性能时需要对推进器全流道进行数值计算,当转子流道内的网格采用整体划分时,各流道之间的网格无法保证完全一致,各个叶片受力受叶片网格的不均匀性的影响。非定常计算需要同时捕捉推进器总力和微小的脉动值。由于各个叶片受力不同,可能对推进器的总力影响不大,但是会影响非定常力的脉动值。为保证转子各流道之间的网格是完全一致的,采用周期性的网格进行非定常分析,即首先生成转子单流道的计算域网格,再将单流道网格旋转复制得到全流道的计算网格。
为研究各流道网格不均匀性对非定常力的影响,分别对推进器在整体网格与周期性网格下的非定常性能进行数值分析,2 套网格保证网格尺度一致,消除网格尺度对计算结果的影响。
2.2.1计算网格对推进器性能的影响
图2与图3分别为 2 套网格下在 J=0.6 时非定常计算推力系数及扭矩系数的时域图。由结果可知,2套网格下非定常计算时推力系数与扭矩系数随时间变化的规律一致,计算到达稳定的时间基本一致,主要差别在数值大小上。
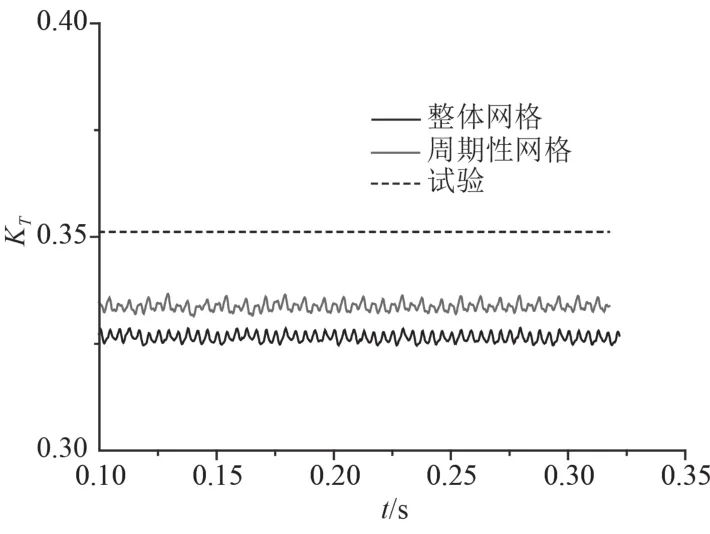
图2 两套网格下的推力系数 KT 时域图(J=0.6)Fig.2 The time domain distribution of thrust coefficient (KT)under two sets of meshes (J=0.6)
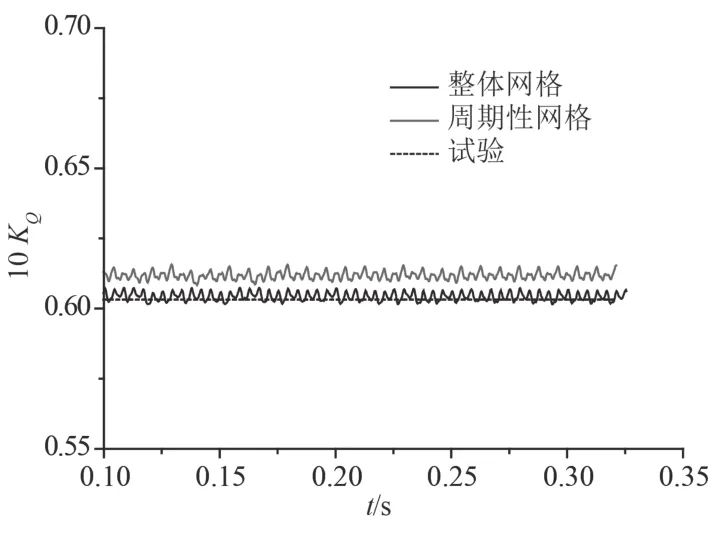
图3 两套网格下的扭矩系数 10 KO 时域图(J=0.6)Fig.3 The time domain distribution of torque coefficient (10 KO)under two sets of meshes (J=0.6)
表3为周期网格下非定常计算后推力系数与扭矩系数值。与表1和表2中的数据相比,周期性网格下定常计算推力系数与扭矩系数计算精度有所降低,然而周期性网格下非定常计算推力系数误差为 4.95%,推力系数计算精度得到提高,误差较小。2 套网格下定常计算时扭矩计算精度比推力计算精度低,但非定常计算下扭矩计算精度得到大幅提高,推力计算精度降低,使得扭矩计算精度比推力计算精度高。
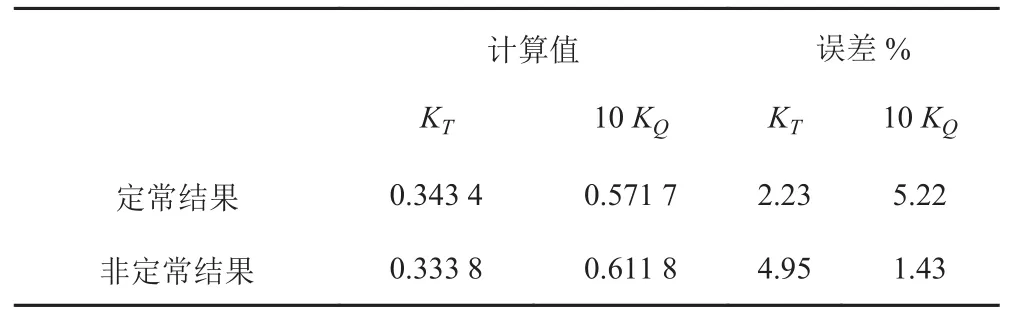
表3 周期性网格下的计算结果(J=0.6)Tab.3 Numerical results under periodic mesh (J=0.6)
2.2.2计算网格对非定常力的影响
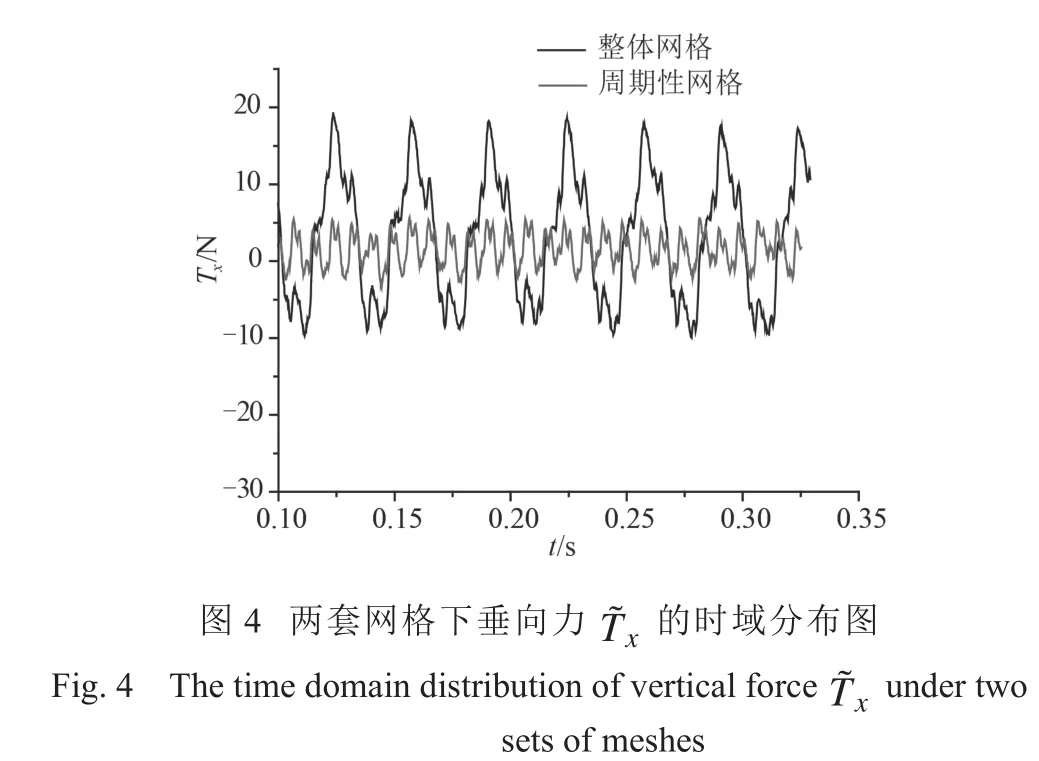
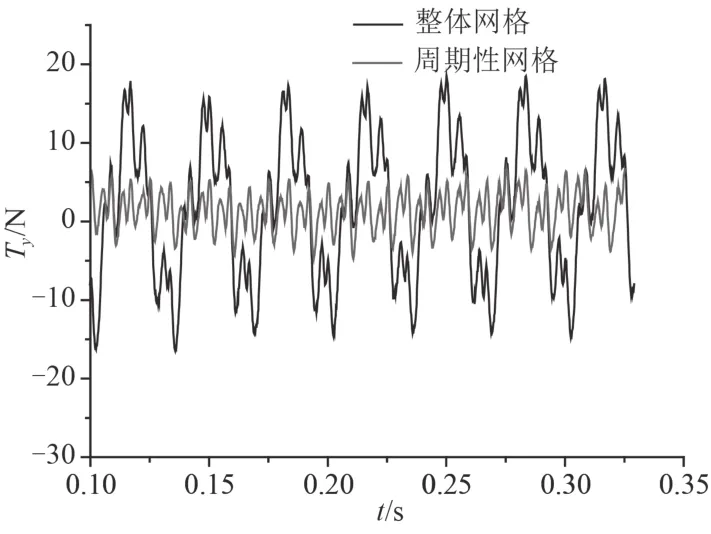
图5 两套网格下径向力 Tv的时域分布图Fig.5 The time domain distribution of radial force Tvunder two sets of meshes
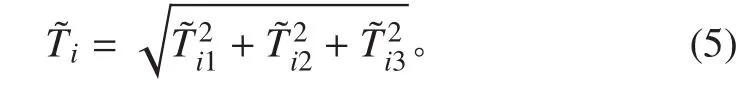
由表4可知,整体网格下轴向平均脉动力为 4.23 N,周期性网格下的轴向平均脉动力为 4.218 N,2 套网格下的脉动强度基本一致。
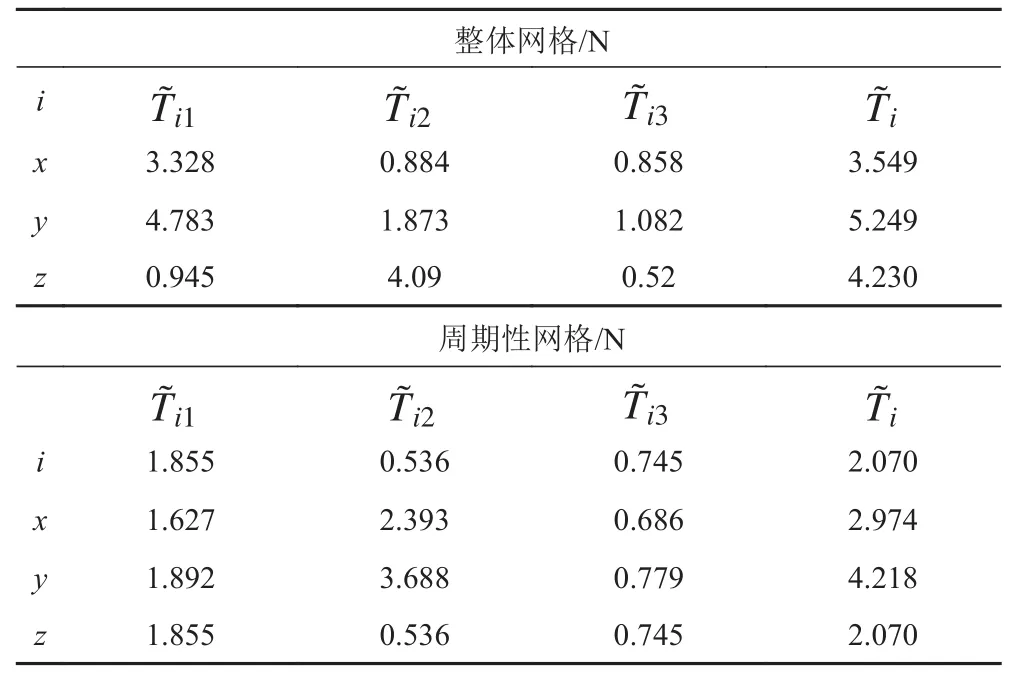
表4 两套网格下 x、y 及 z 方向上前3阶叶频处的非定常力Tab.4 The unsteady force at the first three order blade frequency in x,y,z direction under two sets of meshes
整体网格下 x 方向上的平均脉动力为 3.549 N,y方向上的平均脉动力为 5.249 N;周期性网格下 x 方向上的平均脉动力为 2.07 N,y 方向上的平均脉动力为2.974 N。与周期性网格相比,整体网格下 x 方向与 y方向上的脉动较为剧烈,这即是由于整体网格下各个叶片受力不一致导致额外增加了x 方向与 y 方向上的脉动值。
3 结 语
本文基于滑移网格方法对带前置定子导管式推进器非定常性能数值计算方法进行了研究,主要研究了推进器在不同网格划分方式下的非定常性能。可得到以下结论:
1)与定常计算结果相比,非定常计算下推进器的推力系数计算精度较低,但是能满足要求;
2)与整体网格相比,周期性网格下非定常计算后推力系数计算精度得到提高;
3)与整体网格相比,周期性网格下非定常轴向脉动力基本相同,x 方向与 y 方向上的非定常脉动力明显降低。
[1]潘光,胡斌,王鹏,等.泵喷推进器定常水动力性能数值模拟[J].上海交通大学学报,2013,47(6):932-937.
[2]谭廷寿,贺伟.螺旋桨非定常轴承力计算[J].船海工程,2006,35(2):42-46.
[3]熊鹰.非均匀流中螺旋桨空泡及脉动压力的数值和试验研究[D].武汉:武汉理工大学,2002.
[4]胡小菲,黄振宇,洪方文.螺旋桨非定常力的黏性数值分析[J].水动力学研究与进展,2009,24(6):734-739.
[5]沈海龙,苏玉民.船体黏性非均匀伴流场中螺旋桨非定常水动力性能预报研究[J].水动力学研究与进展,2009,24(2):232-241.
[6]姚震球,高慧,杨春蕾.基于滑移网格的带螺旋桨艇体尾流场数值分析方法[J].江苏科技大学学报(自然科学版),2008,22(2):15-20.
[7]HUGES M J,KINNAS S A.An analysis method for a ducted propeller with pre-swirl stator blades[C]//Proceedings of propeller/shafting's 91 symposium Virginia beach.Virgina,USA:SNAME,1991.
Research on numerical method of the unsteady performance of ducted propulsor
SHU Li-wei
(Navy Equipment Department,Beijing 100841,China)
Based on the sliding mesh method,the SST k-ω turbulent model was adopted to study the influence of different grid generation method on the unsteady performance of ducted propulsor with pre-stator.Firstly,based on the moving reference frame method and the sliding mesh method,the steady and unsteady performance was separately simulated.Then its numerical results were verified by comparing with experimental results.Furthermore,based on the mentioned method,the difference between the model in integral mesh and that in periodic mesh was compared,such as thrust coefficient,torque coefficient and unsteady force in x,y,z direction.The result provides a reference for further unsteady performance study of propulsor.
moving mesh;propulsor;periodic mesh;unsteady force
U664.3
A
1672-7619(2016)07-0026-04
10.3404/j.issn.1672-7619.2016.07.006
2016-04-20
舒礼伟( 1978-),男,工程师,主要从事船舶结构设计工作。
