长甲板室端部应力集中分析及优选设计研究

赖　蕾，张世联（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

长甲板室端部应力集中分析及优选设计研究

赖蕾，张世联
（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

针对长甲板室纵向围壁端部与主船体露天甲板交界处的应力集中问题，采用结构有限元数值分析方法，探讨在空间布置受到限制的条件下，应力集中交界处圆弧型肘板臂长、圆弧半径等参数变化对应力分布和大小的影响，并得到降低应力集中系数的圆弧型肘板参数的最佳值。文中根据研究结果，对某艘实船的长甲板室纵向围壁端部与主船体露天甲板交界处圆弧型肘板进行优选设计，有效地降低了该处的应力集中水平。

长甲板室；应力集中；圆弧形肘板；优选设计

0　引　言

随着海上运输、救援等任务的多样化和特殊化，对船舶结构和布置的要求越来越高。为了加大船舶的装载能力、改善船舶适居性，也为了方便露天甲板上重载设备的布置，在某些具有特殊功能的船舶前部设置了长上层建筑或长甲板室。目前，许多长上层建筑或长甲板室的纵向长度都达到了0.5 倍船长以上，较大程度上参与了总纵弯曲。并且，上层建筑或甲板室与主船体连接处，由于断面形状发生突变，致使其端部应力集中问题突出。一般来说，上层建筑或甲板室侧围壁端部与主船体连接处是应力集中的高危部位。然而，为了满足某些功能需要，一些长甲板室的内部设置了长纵向围壁，其在一定程度上参与了总纵弯曲，此时，在长甲板室内部纵向围壁端部与主船体相交处也存在应力集中问题，其应力甚至大于侧围壁端部的应力。

目前，对长上层建筑侧围壁端部应力集中问题有较多的研究［1-6］，大多推荐采用大圆弧或椭圆弧结构进行过渡优化，CCS 钢规［7］也对该处结构过渡型式及结构尺寸作了相应的规范要求。然而，对于长甲板室的端部应力集中问题，尤其是内部的长纵向围壁端部与主船体露天甲板相交处（以下简称纵向围壁端部）的应力集中问题研究尚少。考虑到该处结构位于船中，为了不妨碍露天甲板上设备的布置，也为了方便船员的行走，其在进行结构设计时受到空间位置的限制，不宜使用尺寸较大的圆弧或椭圆弧过渡。因此，在满足总布置要求的前提下，为了防止该处高应力引起的结构破坏，需对该处附近的应力进行分析，并采取优选的结构设计手段，降低该处的应力集中水平。田旭军等［8］采用遗传算法对一种新型肘板结构型式进行结构优化设计；史战新［9］采用子模型法对三角形肘板和弧形肘板的应力与疲劳寿命进行仿真分析。根据目前的研究成果可知，采用肘板能降低应力集中程度，但是在布置受到限制的前提下，如何选取合适的肘板参数，目前研究尚少。

本文基于结构有限元数值分析方法，探讨在布置空间有限的前提下，应力集中交界处的圆弧型肘板臂长、圆弧半径等参数变化对长甲板室纵向围壁端部应力分布和大小的影响，并采用该种方法对某艘实船纵向围壁端部应力集中问题进行分析及优选设计。

1　简化的长甲板室纵向围壁端部应力集中分析

1.1简化的有限元计算模型

为了分析空间布置受到限制时长甲板室纵向围壁端部的应力分布规律，模拟某一实船的长甲板室纵向围壁结构，对船体结构进行一定的简化，取该船的长甲板室纵向围壁与船舶主体纵向舱壁为研究对象。

模型采用 MSC/PATRAN 有限元结构分析软件进行建模，船体各部分结构均采用板单元模拟，单元尺寸为 700mm，细化区域内网格尺寸为 50mm。船舶总长L=140m，模型选取中后舱段，长度为 l=0.6 L，中后上层建筑长度为舱段长度的33％，内部设置多道横舱壁。材料为普通钢。简化的船中横剖面图以及计算有限元计算模型如图1所示。

计算时在模型的左端施加一单位弯矩 M=1.0 N·m，在模型的右端进行刚性固定，如图1（b）所示。

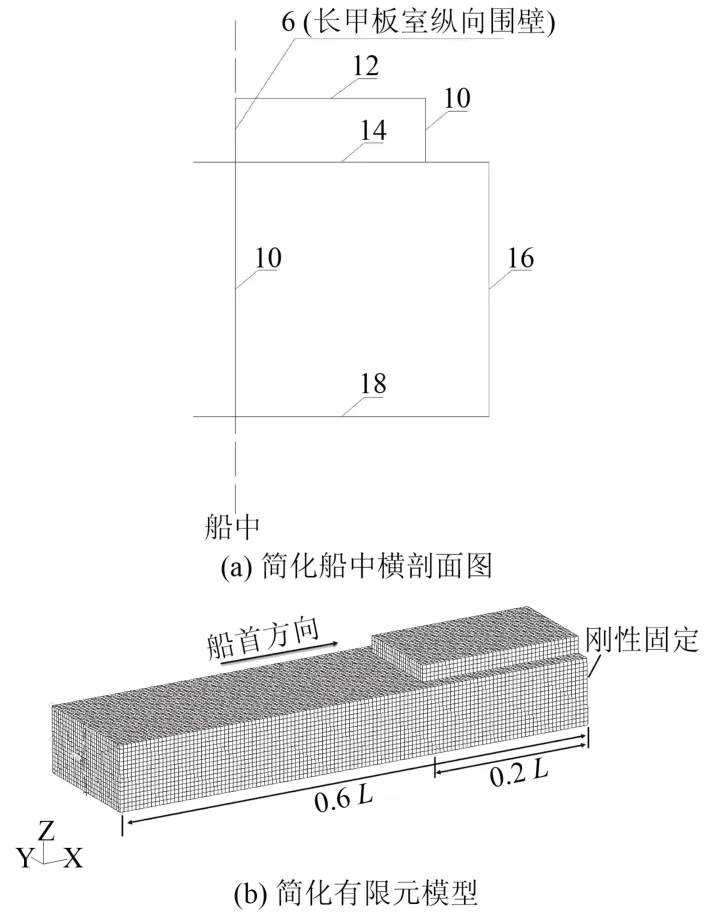
图1　简化的船中横剖面图以及计算有限元计算模型Fig.1　Simplified midship transverse cross-section plan and FE model

1.2端部未加肘板时的计算结果

经有限元计算，长甲板室内部纵向围壁的von Mises应力分布如图2所示。从图中可以看出，长甲板室内部纵向围壁端部与主甲板相连的角隅处产生应力集中。

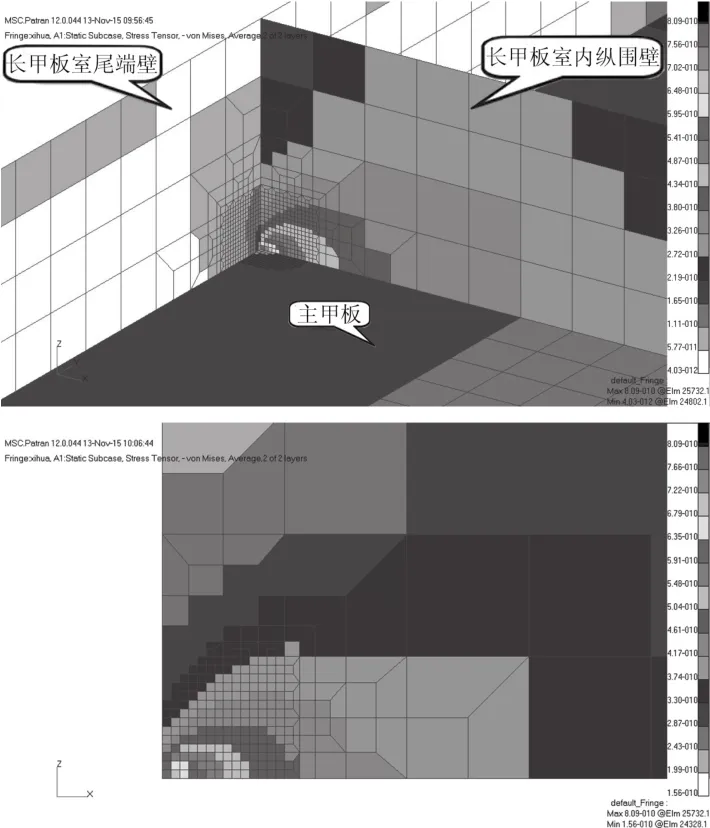
图2　长甲板室端部 von Mises 应力分布图Fig.2　Stress distribution of long deckhouse end

根据船体强度［10］的相关知识，结合有限元模型计算结果分析可知，造成长甲板室内部纵向围壁端部角隅处应力较大的原因主要有2个：一是长甲板室的端点效应，使得其在越接近端点的断面处剪切应力越大；二是由于长甲板室端部与主船体连接之处断面形状发生突然变化，从而引起了长甲板室端部的应力集中。

根据有限元直接计算结果，内部纵向围壁端部处von Mises 应力的最大值和应力集中系数分别为：

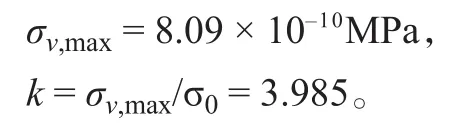
式中：σ0为纯弯矩作用下主船体尾部甲板的应力，σ0=2.03 × 10-10MPa。

1.3端部加圆弧形肘板

1.3.1肘板参数与有限元模型

当长甲板室纵向围壁厚度、主甲板厚度一定时，在长甲板室内部纵向围壁尾端处加装圆弧形肘板，拟研究在单位弯矩 M=1.0 N·m 作用下纵向围壁端部应力分布与肘板型式、肘板尺寸的关系。纵向围壁端部附近的应力分布与圆弧形肘板臂长 a（与上层建筑尾端壁相连）、b（与主甲板相连）、肘板圆弧半径 R 有关，但由于受到总布置的限制，肘板尺寸不宜过大，因此计算时选取如下肘板参数进行研究：

肘板臂长：a=300mm，500mm，700mm；b=300mm，500mm，700mm；

肘板圆弧半径：R=无穷大（即直线型肘板），500mm，700mm，900mm，1 100mm，1 500mm 及2 000mm。

1.3.2纵向围壁端部及肘板应力分布

经有限元计算，加装肘板后，围壁端部处的von Mises 应力分布如图3所示，此时与未加肘板相比（见图2），应力最大值的位置发生了变化。从图3（a）可知，在肘板参数选取不当的情况下，肘板趾端会成为新的应力集中点，其应力甚至超过未加肘板时围壁端部的最大应力。而采用圆弧型肘板，可以明显改善趾端硬点处的应力集中现象，并明显降低纵向围壁端部的应力水平，如图3（b）所示。图3表明采用圆弧型肘板可使原来端壁的结构突变现象得到改善，从而改变了该处端壁角隅点的受力状态，达到降低应力集中的目的。

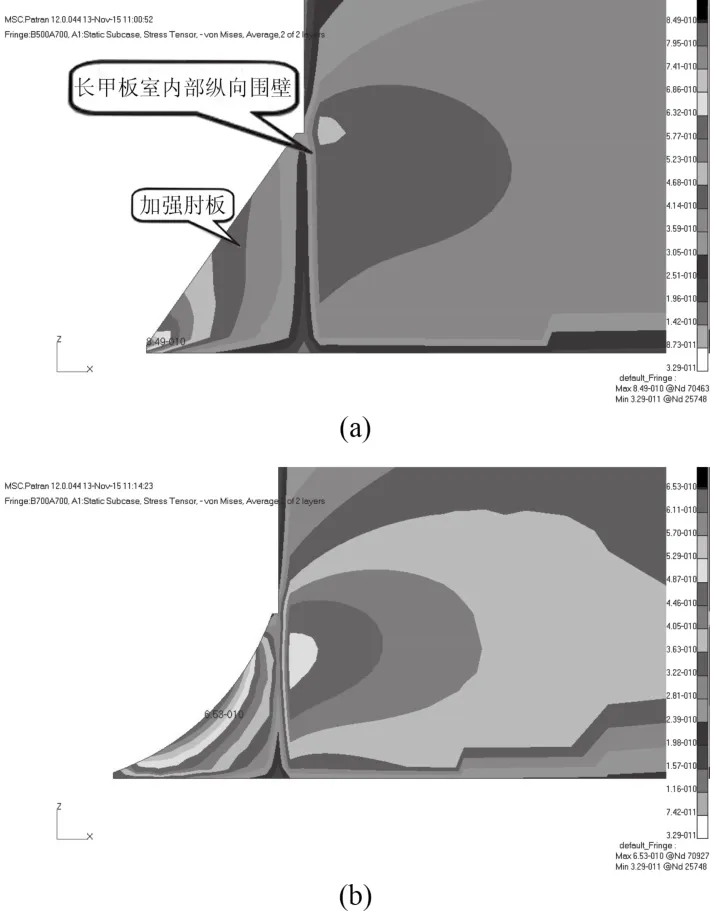
图3　纵向围壁端部加装肘板后的典型 von Mises 应力分布图Fig.3　Typical stress distribution of long deckhouse end with brackets

为了得到最佳的圆弧形肘板设计参数，在对纵向围壁端部圆弧形肘板进行不同参数设计时，根据船舶总布置的要求确定可接受的肘板臂长 b。通过对不同参数的圆弧形肘板进行有限元计算和结果整理，可给出在 b 一定时，变化 a以及 R 后围壁端部结构应力集中系数 k 随肘板臂长比 a/b的变化关系，如图4所示。图4中给出不同肘板圆弧半径 R 对应的等值线。从图中可以看出，肘板的尺寸并非越大越好。在 b 一定时，若肘板的臂长比过小或过大，围壁端部的应力均有可能超过安装肘板前的应力。因此，选取合适的臂长比非常重要，当臂长比一定时，可通过变化肘板圆弧半径使应力水平达到最低。从图4中可以看出，对应不同的R，应力集中系数 k 均在 a/b=1.0 附近达到最小值，因此在进行优化时，在总布置允许的前提下，应尽可能使肘板的臂长比接近 1。

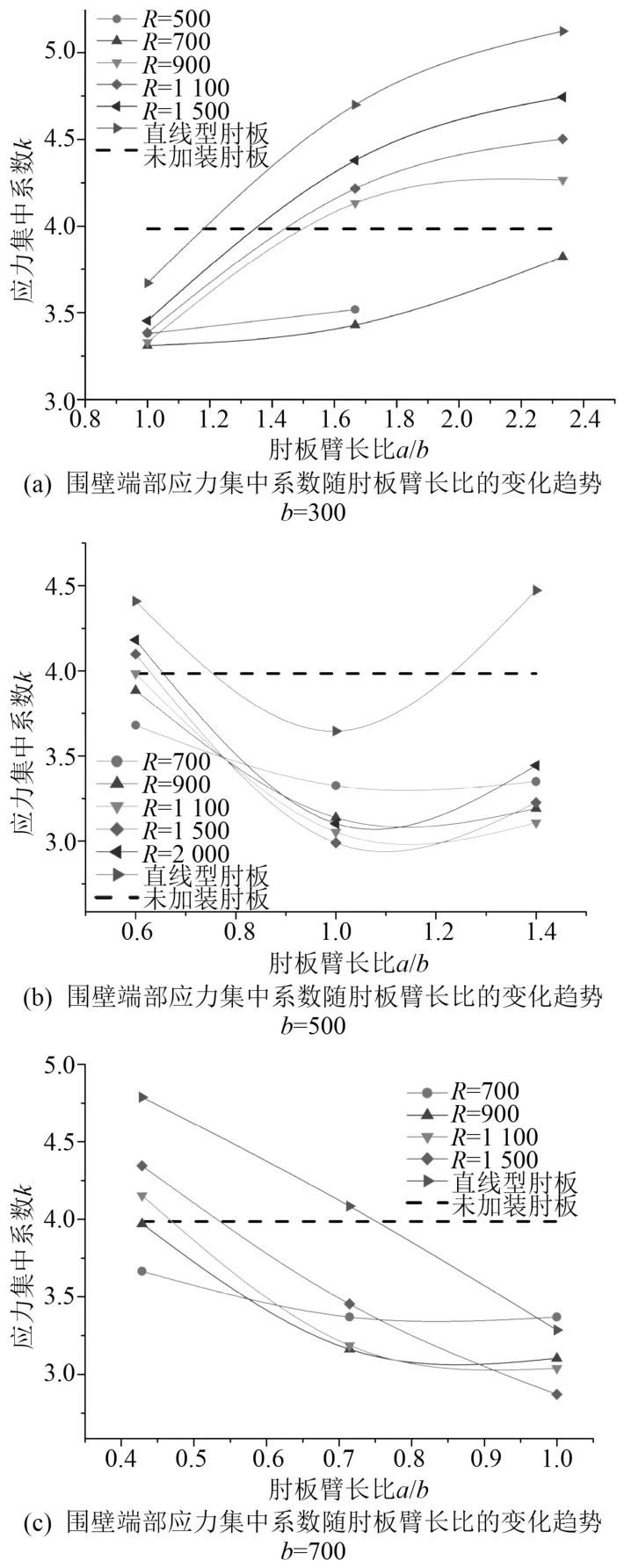
图4　纵向围壁端部应力集中系数 k 随肘板臂长比 a/b和圆弧半径 R的变化曲线Fig.4　Stress concentration factor （SCF）k of longitudinal wall end versus a/b and R

取臂长比 a/b=1，b 不同时，纵向围壁端部结构应力集中系数 k 随肘板圆弧半径 R的变化如图5所示。从图5可看出，b 越大纵向围壁端部的应力集中水平越低；此外，b 一定时，k 随着 R的增大呈现出先减小后增大的趋势。这是由于采用圆弧型肘板时，应力集中现象主要出现在圆弧上，当肘板的臂长一定时，圆弧曲率减小则应力集中程度也相应减小，但当 R 增大到一定值后，肘板趾端变为硬点，成为新的应力集中点，此后应力会随着 R的增大而增加。可见，在空间布置允许的前提下，应选择较大的肘板臂长；并且，对于不同的肘板臂长，存在最优的圆弧半径 R，使得纵向围壁端部的应力值最小，此时，围壁角隅处的应力集中现象得到改善，围壁端部的应力分布更为均匀，从而增加了结构的寿命。

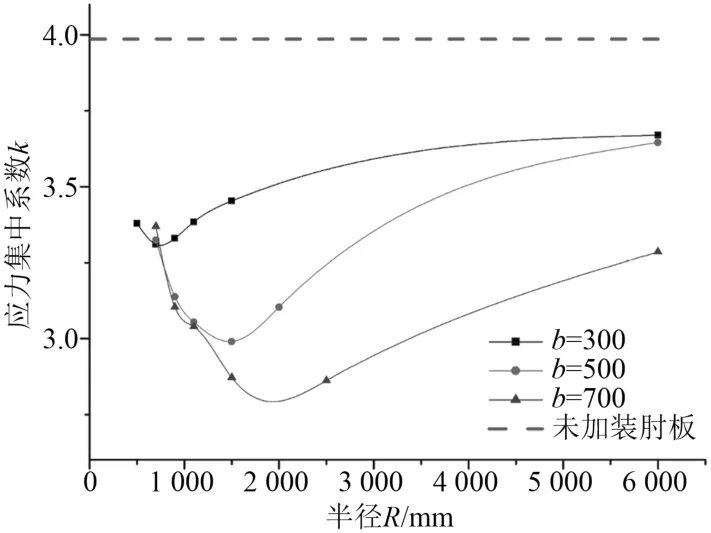
图5　纵向围壁端部应力集中系数 k 随肘板圆弧半径 R的变化趋势Fig.5　SCF k versus R

2　实船长甲板室纵向围壁端部结构设计

从第1节的讨论可知，在不影响总布置的前提下，采用圆弧形肘板能有效改善纵向围壁端部的应力集中现象。为了验证上述讨论结果的适用性，将圆弧形肘板设计应用到1艘特种船体的长甲板室尾端部优化设计中。

实船船体中后部有较大面积的露天甲板，上面布置了各种重型设备；长甲板室长度约为 3/5 船长，其尾端壁部在船舯后约 1/10 船长处结束。其侧围壁与尾端壁之间采用圆弧型过渡型式。此外，出于总布置的需求，距船中一个纵骨间距处设置了长纵向围壁，长约 1/5 船长，长甲板室围壁均采用 DH36 高强度钢建造。其结构有限元模型如图6所示。

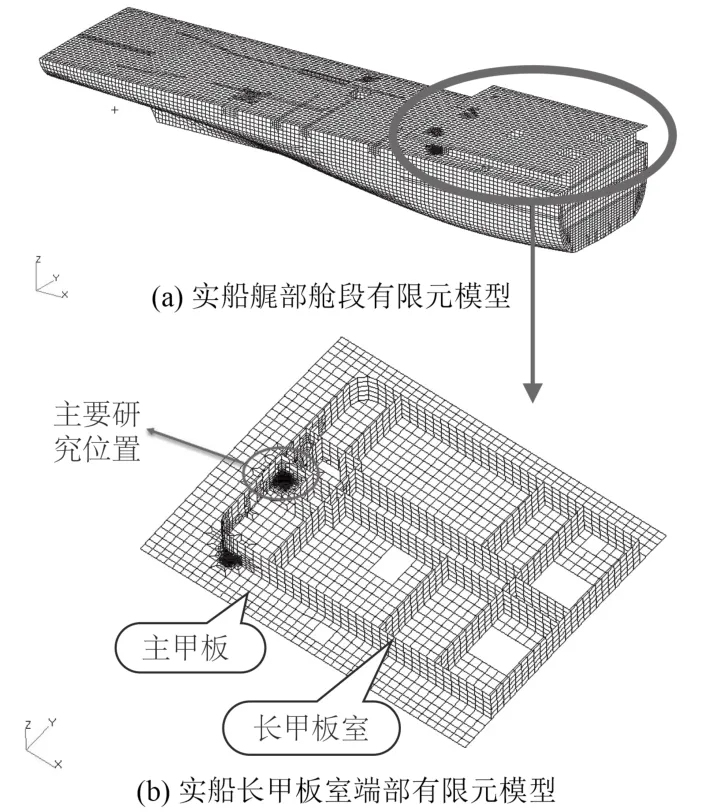
图6　实船结构有限元模型Fig.6　FE model of a real ship

计算结果显示，单元 von Mises 应力最大值出现在长甲板室内部长纵向围壁端部与主甲板相连的角隅处，为：

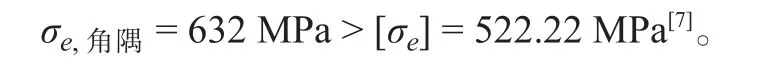
根据 CCS 钢质海船入级规范 2014年修改通报［7］的相关规定，其不满足高强度钢的应力衡准。为此，需对该处结构形式进行优化。由于该船总布置的限制，其结构型式不能随意改变，因此可通过增加端部附近板厚或者加装圆弧型肘板的方法对其进行优化。

2.1增大纵向围壁端部附近结构尺寸

为使该处的应力水平满足许用衡准的要求，将纵向围壁端部角隅附近的纵向围壁厚度由 10mm 增加为16mm，并将主甲板厚度由 14mm 调整为 20mm，横向围壁板厚由 10mm 增加至 14mm。此时，结构重量增加了166.21kg。

调整板厚后长甲板室尾端壁附近单元 von Mises 应力分布见图7所示。可见，改变板厚降低了该处的应力值，但应力分布状态改变不大，应力最大值仍位于长甲板室内部纵向围壁端部与主甲板相接的角隅处，单元 von Mises 应力为：

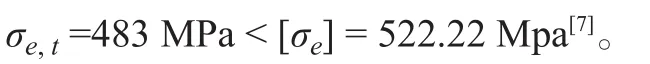
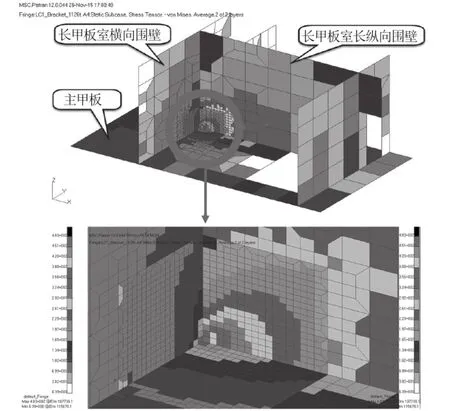
图7　调整板厚后长甲板室尾端壁附近单元 von Mises 应力分布图Fig.7　Stress distribution of long deckhouse end

根据 CCS 钢质海船入级规范 2014年修改通报［7］，该应力满足高强度钢的应力衡准。

2.2圆弧形肘板加强

根据第1节对圆弧形肘板参数的研究，在纵向围壁端部所选肘板的臂长应尽量大，臂长比应接近 1，并且存在最优的圆弧半径使得纵向围壁端部的应力水平得到有效的降低。结合本船总布置的要求，选取肘板尺寸为：肘板臂长 a=b=450mm，肘板板厚 t=12mm，肘板圆弧半径 R=1 000mm，重量约为 9kg。

此时，长甲板室纵向围壁端部应力水平得到较大幅度的下降，单元 von Mises 应力分布如图8所示，应力最大值出现在肘板圆弧上。

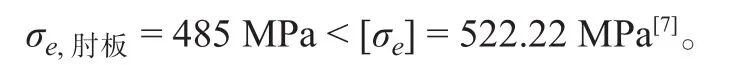
根据 CCS 钢质海船入级规范 2014年修改通报［7］，该应力满足高强度钢的应力衡准。

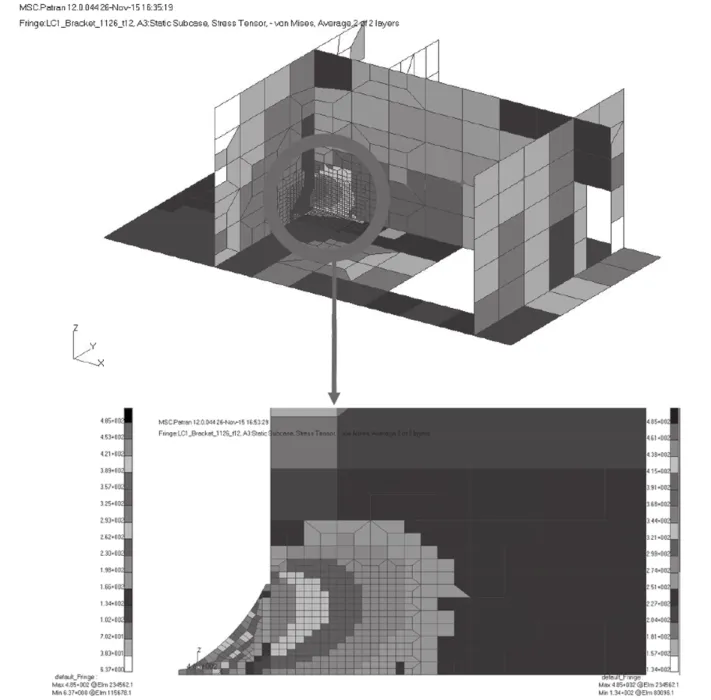
图8　加装肘板后长甲板室尾端壁附近单元 von Mises 应力分布图Fig.8　Stress distribution of long deckhouse end with a bracket

从图8中可以看出，设置圆弧形肘板过渡改变了长甲板室纵向围壁尾端附近的应力分布形式，对减小纵向围壁端部应力集中现象有明显的作用，与第1节的讨论相符。单元 von Mises 应力最大值出现在肘板圆弧上，较未加强时结构应力的最大值有所下降。可见，加装圆弧形肘板能有效改善该船长甲板室纵向围壁端部的应力集中程度，达到降低应力水平的目的。

2.3小结

以上优化方式对长甲板室内部长纵向围壁端部应力大小的影响见表1。

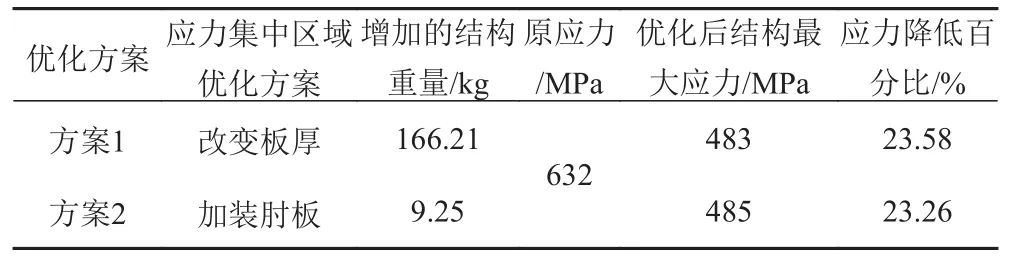
表1　各优化方案及计算结果Tab.1 The optimization scheme and the calculation result

可见，以上优化方案都能在一定程度上起到降低长甲板室纵向围壁端部应力集中水平的作用。当采用增加板厚的方法时，为使应力满足许用衡准，长甲板室结构重量增加了166.21kg，与方案2相比，方案1较为不经济。

对于在围壁末端加装圆弧型肘板过渡的结构型式，其在不影响总布置的前提下，改变了长甲板室围壁端部附近的应力分布形式，该方法采用材料较少，占用空间较小，并对减小端部应力集中现象有明显的作用。在加装肘板后，端部应力达到许用衡准，这对于长甲板室纵向围壁端部结构优化具有一定的指导意义。

3　结 语

在总布置受到限制的前提下，通过研究不同的圆弧形肘板尺寸参数对长甲板室纵向围壁端部应力分布和大小的影响，得到以下结论：

1）在长甲板室纵向围壁末端加装圆弧型肘板能改变该处的应力分布形式，有效降低该处的应力集中；

2）采用肘板对长甲板室端部结构进行加强时，在不影响总布置的前提下，应尽可能使肘板的臂长比接近于 1；

3）在圆弧形肘板臂长比接近于 1 时，纵向围壁端部的应力随肘板圆弧半径的增加呈现出先降低后升高的趋势，圆弧半径有最佳值。

［1］何祖平，王福花，王德禹.舰船上层建筑端部及舷侧大开口应力集中分析和光弹性实验［J］.中国造船，2006，47（1）：84-89.

［2］陈倩.铝合金上层建筑参与总纵弯曲的有效程度研究［D］.上海：上海交通大学，2011.

［3］李源源，孙巍.长桥楼上层建筑结构设计分析［J］.中国舰船研究，2014，9（3）：57-61，68.

［4］WU Wei-guo，DUAN Hong，PEI Zhi-yong，et al.Experiment research of stresses along the junction lines between the superstructure and the deck［J］.Journal of Ship Mechanic，2002，6（3）：62-68.

［5］赵尚辉，黄守成.某平底浅吃水船上层建筑应力集中分析及改善措施［J］.船舶工程，2006，28（6）：28-30.

［6］朱云翔.长上层建筑结构设计有关问题的探讨［J］.船海工程，2013，42（3）：29-33.

［7］中国船级社.钢质海船入级与建造规范［M］.人民交通出版社，2012.

［8］田旭军，闫国强，胡刚义.基于遗传算法的肘板结构型式优化［J］.中国舰船研究，2007，2（2）：23-26.TIAN Xu-jun，YAN Guo-qiang，HU Gang-yi.Optimization of bracket plate using genetic algorithm［J］.Chinese Journal of Ship Research，2007，2（2）：23-26.

［9］史战新.基于Ansys子模型法的肘板结构优化［J］.舰船科学技术，2014，36（8）：19-26.SHI Zhan-xin.The bracket structure optimization based on ansys sub-model method［J］.Ship Science and Technology，2014，36（8）：19-26.

［10］杨代盛.船体强度与结构设计［M］.北京：国防工业出版社，1982.

Analysis and optimum design on the stress concentration of long deckhouse end

LAI Lei，ZHANG Shi-lian
（School of Naval Architecture Ocean and Civil Engineering，Shanghai Jiaotong University，Shanghai，200240）

Long deckhouse casing ends often have stress concentration problems，and such a problem can be alleviated through planting a circular-arc bracket on the end of longitudinal deckhouse casing.In this paper，under the condition which the space layout of a ship is restricted，a study based on the structural finite element method is implemented to investigate the optimum effects of brackets with different sizes，namely bracket arm length and radius of circular-arc.According to the calculation results，two arms of a bracket should have equal length and the circular-arc radius has the optimal value so that an optimum design of circular-arc bracket can be presented.Based on the study results，an optimization design is carried out on a real ship by planting a circular-arc bracket in order to reduce the stress concentration on the connection of long deckhouse casing end and the main deck，which can serve as a good reference for production design.

long deckhouse；stress concentration；circular-arc bracket；optimum design

U 661.4

A

1672-7619（2016）07-0006-05

10.3404/j.issn.1672-7619.2016.07.002

2015-11-30；

2016-01-06

赖蕾（1992-），女，硕士研究生，主要从事船舶海洋结构设计相关研究工作。