Banach空间中分层不动点的 黏性连续型广义逼近格式的收敛性
2016-09-29王元恒
王元恒, 谢 飞
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
Banach空间中分层不动点的 黏性连续型广义逼近格式的收敛性
王元恒,谢飞
(浙江师范大学 数理与信息工程学院,浙江 金华321004)
主要在更广泛的自反Banach空间中给出一种求非扩张映像T的分层不动点的新的黏性隐形连续型广义逼近迭代算法,并在一定条件下证明了这种迭代程序强收敛于T的一个分层不动点,同时此点也是一个在优化理论中有着重要应用的广义变分不等式的解.其结果推广和改进了一些近代已有的结果.
非扩张映像;变分不等式解;分层不动点;黏性逼近;强收敛性
0 引 言
设E为赋范线性空间,映射T:E→E.若
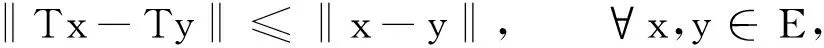
则称T为非扩张映像.用Fix(T)表示T的不动点集,即Fix(T)={x∈E:Tx=x}.
对于映射f:E→E,若存在一个常数α∈(0,1)和∀x,y∈E,使得
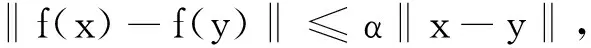
则称f在E上是压缩的.用ΠE表示E上的所有压缩映像集族,即ΠE={f:f在E上压缩}.
非扩张映射的一个经典研究方法就是用压缩映射不动点逼近非扩张映射不动点[1-3],更确切地,给出t∈(0,1),并定义一个压缩映射Tt:E→E,有
其中,u∈E为一个给定的点.Banach压缩映射原理能保证Tt在E中有唯一不动点xt.文献[2]将文献[1]的结论推广到Banach空间,并证明了:若E是一致光滑Banach空间,则xt强收敛到T的不动点x*,t→0.文献[3]证明了文献[2]的结论在含有一个弱连续对偶映射的自反Banach空间中仍然成立.
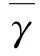
(1)
一个经典的优化问题就是关于实Hilbert空间上非扩张映射不动点集的二次极小化问题
(2)
式(2)中:C是H上非扩张映射T的不动点集;b是H内给定的一个点.文献[6]给出了下面迭代法中定义的序列{xn}:
(3)
式(3)中,x0∈H给定.在{αn}满足一定的条件下,文献[6]还证明了此序列 {xn} 强收敛到极小化问题(2)的唯一解.
近年来,许多学者[7-13]利用黏性逼近法对广义非扩张映射的不动点和变分不等式的解进行了统一联合研究.文献[14]对非扩张映射引进了下面黏性迭代序列{xn}:
(4)
式(4)中:f是H上压缩映射;任意选定x0∈H,序列{σn}⊂(0,1).在{σn} 满足一定合适条件下,文献[14]证明了由式(4)生成的序列{xn}强收敛到变分不等式
的唯一解x*.
结合迭代法(3)和(4),文献[15]考虑并证明了下面一般迭代法:
(5)
在系数{αn}满足适当条件时,由式(5)生成的序列{xn}强收敛到下面变分不等式的唯一解:
这也正是最小化问题
的最优化条件解,其中h是γf的势(即h′(x)=γf(x),∀x∈H).
文献[16]介绍了用下面的混合迭代法解变分不等式:
(6)
式(6)中:F是一个k-Lipschitzian和η-强单调算子;k>0;η>0;0<μ<2η/k2.若λn满足适当条件,文献[16]还证明了由式(6)生成的序列{xn}强收敛到下面变分不等式的唯一解:
特别地,文献[17]在Hilbert空间中考虑了下面较一般的迭代法:
(7)
在序列{αn}的系数满足适当条件下,文献[17]还证明了由式(7)生成的序列{xn}强收敛到下面变分不等式的唯一解x*∈C:
其中,C=Fix(T)为分层不动点集.最近,文献[18]将文献[17]的结果由Hilbert空间推广到Banach空间,并给出了更广泛的分层不动点迭代序列及其收敛性定理.
受到上述结果的启发,本文给出Banach空间E上的一种更加广泛的黏性隐式连续型广义迭代逼近格式
(8)

其中:φ:[0,∞)→[0,∞)是度规函数;Jφ是Banach空间E上的φ正规对偶映射.
显然,若E是Hilbert空间且φ是恒等函数,则Jφ是E上的恒等映射,于是这里的Banach空间上的分层不动点问题就变成了过去Hilbert空间上的分层不动点问题;若f(x)=u,∀x∈E为常值算子,则这里的黏性问题就变成了一般压缩型迭代问题;若F是恒等算子,则这里的关于F的广义变分不等式就变成了过去的一般变分不等式;若取t=αn→0,n→∞,则这里的连续型迭代格式xt就变成了一般序列形式的迭代格式xn.所以,本文结果在一定意义上改进和推广了许多已有的近代结果[1-18].
1 预备知识
本文总假设E是一个自反Banach空间,E*是E的对偶空间.用xn⇀x表示序列xn弱收敛到x;xn→x表示xn强收敛到x.
度规函数φ:[0,∞)→[0,∞),是指当t→∞时,φ为严格连续增函数,且φ(0)=0和φ(t)→∞,t→∞.关于度规函数φ的对偶映射Jφ:E→2E*定义如下:
显然,若取φ(t)=t,则对偶映射Jφ=J即为通常的正规对偶映射;空间lp(1 则 其中,∂ 表示凸分析中Φ(t)的次微分. 引理1[5]假设{an}是一个非负实数序列,满足 其中序列{αn}⊂(0,1)和序列{bn}满足: 引理2[19]假设Banach空间E含有一个弱连续对偶映射Jφ,其中φ是度规函数,则有下述结论: 1)对所有x,y∈E,以下不等式成立: 特别地,对所有x,y∈E,有 2)若E上的序列{xn}弱收敛到点x∈E,则下列等式成立: 引理3[20]设K是Banach空间E上闭凸子集,T:K→K是非扩张映射且Fix(T)≠Ø.若序列{xn}在K上弱收敛到x且(I-T)xn强收敛到y,则(I-T)x=y. 容易证明下述引理: 引理4设E是Banach空间,f:E→E是压缩映射.其中:系数α满足0<α<1;F:E→E是k-Lipschitzian算子和η-强单调算子,且 其中:k>0;η>0.则对于0<γ<μη/α, 即μF-γf是具有系数μη-γα的强单调算子. 定义1设Banach空间E有一个弱连续对偶映射Jφ,φ是度规函数,I是E恒等映射,F:E→E是k-Lipschitzian算子.若存在一个常数τ>0,有下面的性质: (9) ‖αI-βμF‖=sup‖x‖≤1|〈(αI-βμF)x,Jφ(x)〉|,α∈[0,1],β∈[-1,-1], 则称F为(关于φ的具有系数τ的)强正定增生算子.显然,若E=H是实Hilbert空间,则不等式(9)即是式(1).下面的引理在本文主要结论证明中可应用到: 引理5假设Banach空间E有一个弱连续对偶映射Jφ,其中φ是度规函数,F:E→E是k-Lipschitzian和τ强正定增生算子.若常数ρ:0<ρ<φ(1)‖μF‖-1,则‖I-ρμF‖≤φ(1)(1-ρτ). 即I-ρμF是正的.所以由式(9)得 ‖I-ρμF‖=sup{〈(I-ρμF)x,Jφ(x)〉:x∈E,‖x‖=1}= sup{φ(1)-ρ〈μFx,Jφ(x)〉:x∈E,‖x‖=1}≤φ(1)-ρτφ(1)=φ(1)(1-ρτ). 引理5证毕. 下面总假设Banach空间E有一个弱连续对偶映射Jφ,φ是度规函数,且在[0,1]上是不变的,即φ([0,1])⊂[0,1].T是E上的非扩张映射,Fix(T):={x∈E:Tx=x}≠Ø.F在E上是k-Lipschitzian且η-强正定增生算子,k>0,η>0.f在E上是一个压缩自映射:∀x,y∈E,‖f(x)-f(y)‖≤α‖x-y‖,α∈[0,1)是一个常数. 给定f∈ΠE,0<α<1.设t∈(0,1),0<μ<2η/k2,0<γ<μφ(1)(η-μk2/2)/α:=τφ(1)/α,将E上的映射St定义为 则对∀t∈(0,1),St是压缩映射.事实上, ‖Stx-Sty‖≤tγ‖f(x)-f(y)‖+‖(I-μtF)Tx-(I-μtF)Ty‖≤ tγα‖x-y‖+‖I-tμF‖‖Tx-Ty‖≤tγα‖x-y‖+φ(1)(1-tτ)‖x-y‖≤ [1-t(φ(1)τ-γα)]‖x-y‖, (10) 所以,由Banach压缩映射原理知,St在E上存在唯一不动点xt,使得式(8)成立.这正是连续型迭代格式(8)的由来. 显然,这样的Banach空间E是存在的,例如lp(1 (11) 证明证明过程将分为 5 步. (12) 且 (13) 将式(12)和式(13)相加,得 而对任意的x,y∈E,有 〈(μF-γf)x-(μF-γf)y,Jφ(x-y)〉= 〈μF(x-y),Jφ(x-y)〉-γ〈f(x)-f(y),Jφ(x-y)〉≥τφ(‖x-y‖)-γαφ(‖x-y‖)= (τ-γα)φ(‖x-y‖)≥(τφ(1)-γα)φ(‖x-y‖)≥0, 所以必有 第2步证明式(8)中的xt是有界的.取p∈Fix(T),则可以得到 ‖xt-p‖=‖tγf(xt)+(I-tμF)Txt-p‖=‖(I-μFt)Txt-(I-tμF)p+t(γf(xt)-μF(p))‖≤ φ(1)(1-tτ)‖xt-p‖+t(γα‖xt-p‖+‖γf(p)-μF(p)‖), 从而 所以{xt}是有界的,从而{f(xt)}和{μFT(xt)}也是有界的. 第3步令Ww={w∈E:∃tn→0, s.t.xtn⇀w},则∀w∈Ww,Tw=w. 由式(8)知 由Banach空间E的自反性和序列{xt}的有界性知,Ww≠Ø.对∀w∈Ww,存在{xt}的子序列{xtn}弱收敛到w∈E,n→∞,tn→0.因为Jφ是弱序列连续的,所以可由引理2得到:对所有x∈E, 令 则 因为当n→0时, 所以 (14) 另一方面, (15) 由式(14)和式(15)得 从而得Φ(‖T(w)-w‖)=0,Tw=w. 第4步证明当n→∞时,xtn→w. 于是,由引理1得 Φ(‖xtn-w‖)=Φ((I-tnμF)Txtn-(I-tnμF)w+tn(γf(xtn)-μF(w)))= Φ(‖(I-tnμF)Txtn-(I-tnμF)w‖)+tn〈γf(xtn)-μF(w),Jφ(xtn-w)〉≤ Φ(φ(1)(1-tnτ)‖xtn-w‖)+tnγ〈f(xtn)-f(w),Jφ(xtn-w)〉+ tn〈γf(w)-μF(w),Jφ(xtn-w)〉≤ φ(1)(1-tnτ)Φ(‖xtn-w‖)+tnγ‖f(xtn)-f(w)‖‖Jφ(xtn-w)‖+ tn〈γf(w)-μF(w),Jφ(xtn-w)〉≤ φ(1)(1-tnτ)Φ(‖xtn-w‖)+tnγα‖xtn-w‖‖Jφ(xtn-w)‖+ tn〈γf(w)-μF(w),Jφ(xtn-w)〉= φ(1)(1-tnτ)Φ(‖xtn-w‖)+tnγαΦ(‖xtn-w‖)+tn〈γf(w)-μF(w),Jφ(xtn-w)〉= (1-tn(τφ(1)-γα))Φ(‖xtn-w‖)+tn〈γf(w)-μF(w),Jφ(xtn-w)〉. 移项合并得 (16) 由xtn⇀w和Jφ的弱连续性知式(16)的右端趋向于0.于是Φ(‖xtn-w‖)→0,n→∞.所以,当n→∞时,xtn→w. 第5步最后证明w是变分不等式(11)的解. 对∀z∈Fix(T),有 〈(I-T)xt-(I-T)z,Jφ(xt-z)〉=〈xt-z,Jφ(xt-z)〉+〈Txt-Tz,Jφ(xt-z)〉= Φ(‖xt-z‖)-〈Tz-Txt,Jφ(xt-z)〉≥Φ(‖xt-z‖)-‖Tz-Txt‖‖Jφ(xt-z)‖≥ Φ(‖xt-z‖)-‖z-xt‖‖Jφ(xt-z)‖=Φ(‖xt-z‖)-Φ(‖xt-z‖)=0. 由式(8)可以推出 (17) 注意到xtn-Txtn→w-T(w)=w-w=0,现在用tn替换式(17)中的t,并令n→∞,就有 定理1的结果,在比一致凸更广泛的自反Banach空间中,把正规对偶映射J推广到度规函数对偶映射Jφ;把离散型迭代序列推广成连续型迭代格式.从定理1的证明过程可以看出,其证明的思想方法也具有创新性,先证明一个集合中的每个元素都是变分不等式(13)的解,再由解的唯一性说明这个集合就是单点集,也即说明了黏性隐式广义连续型迭代格式(8)的强收敛性.所以,本文的结果在一定意义上从许多方面改进和推广了许多已有的近代结果(如文献[1-18]). [1]BrowderFE.FixedpointtheoremsfornoncompactmappingsinHilbertspaces[J].ProcNatlAcadSciUSA,1965,53(6):1272-1276. [2]ReichS.StrongconvergencetheoremsforresolventsofaccretiveoperatorsinBanachspaces[J].JMathAnalAppl,1980,75(1):287-292. [3]XuHK.Strongconvergenceofaniterativemethodfornonexpansiveandaccretiveoperators[J].JMathAnalAppl,2006,314(2):631-643. [4]DeutschF,YamadaI.Minimizingcertainconvexfunctionsovertheintersectionofthefixedpointsetsofnonexpansivemappings[J].NumerFunctAnalOptim,1998,19(1):33-56. [5]XuHK.Iterativealgorithmsfornonlinearoperators[J].JLondonMathSoc,2002,66(1):240-256. [6]XuHK.Aniterativeapproachtoquadraticoptimization[J].JOptimTheoryAppl,2003,116(3):659-678. [7]李柳红,王元恒.渐近非扩张型映像不动点的粘性逼近法[J].浙江师范大学学报:自然科学版,2015,38(1):41-46. [8]PlubtiengS,ThammathiwatT.Aviscosityapproximationmethodforequilibriumproblems,fixedpointproblemsofnonexpansivemappingsandageneralsystemofvariationalinequalities[J].JGlobOptim,2010,46(3):447-464. [9]金坚帅,倪仁兴.Banach空间中一族依中间意义渐近拟φ-非扩张映射和均衡问题的强收敛性定理[J].浙江师范大学学报:自然科学版,2015,38(2):163-171. [10]XuHK.Viscosityapproximationmethodsfornonexpansivemappings[J].JMathAnalAppl,2004,298(1):279-291. [11]董家帅,王元恒,罗红平.渐近非扩张型映像的黏性三步迭代序列强收敛性[J].浙江师范大学学报:自然科学版,2012,35(3):241-245. [12]邓伟奇.分层变分包含问题中经由分层不动点途径的黏性方法[J].数学物理学报:A中文版,2014,34(5):1254-1263. [13]张石生,王雄瑞,李向荣,等.分层不动点及变分不等式的粘性方法及应用[J].应用数学和力学,2011,32(2):232-240. [14]MoudafiA.Viscosityapproximationmethodsforfixed-pointsproblems[J].JMathAnalAppl,2000,241(1):46-55. [15]MarinoG,XuHK.AgeneraliterativemethodfornonexpansivemappinginHilbertspaces[J].JMathAnalAppl,2006,318(1):43-52. [16]YamadaI.Thehybridsteepestdescentforthevariationalinequalityproblemsovertheintersectionoffixedpointssetsofnonexpansivemapping[M]//ButnariuD,CensorY,ReichS.Inherentlyparallelalgorithmsinfeasibilityandoptimizationandtheirapplication.Amsterdam:Elservier,2001:473-504. [17]TianM.AgeneraliterativealgorithmfornonexpansivemappingsinHilbertspaces[J].NonlinearAnalysis,2010,73(3):689-694. [18]WangYuanheng,XuWei.Strongconvergenceofamodifiediterativealgorithmforhierarchicalfixedpointproblemsandvariationalinequalities[J].FixedPointTheoryandApplications,2013,2013(121):1-9. [19]LimTC,XuHK.Fixedpointtheoremsforasymptoticallynonexpansivemappings[J].NonlinearAnal,1994,22(11):1345-1355. [20]WangYH,XiaYH.StrongconvergenceforasymptoticallypseudocontractionswiththedemiclosednessprincipleinBanachspaces[J].FixedPointTheoryandApplications,2012,2012(45):1-8. (责任编辑陶立方) The convergence for a generalized viscosity implicit iteration to approximatea hierarchical fixed point of nonexpansive mappings in Banach spaces WANG Yuanheng,XIE Fei (CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China) A generalized viscosity implicit continuous iterative method was introduced to approximate a hierarchical fixed point of nonexpansive mappings, which was also a solution of a variational inequality in Banach spaces. Under certain approximate assumptions of the operators and coefficients, the strong convergence for the generalized iteration was obtained by some certain techniques in Bananch spaces. The results extended and improved many recent results announced by other authors. nonexpansive mapping; solution of variational inequality; hierarchical fixed point; viscosity iterative approximating; strong convergence 10.16218/j.issn.1001-5051.2016.03.002 收文日期:2016-02-20;2016-03-13 国家自然科学基金资助项目(11271330);浙江省自然科学基金资助项目(LY14A010011) 王元恒(1961-),男,河南南阳人,教授.研究方向:非线性泛函分析. O177.91 A 1001-5051(2016)03-0246-07

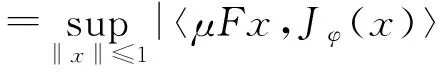
2 主要结果



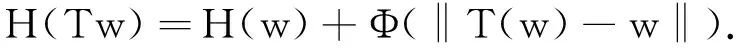



3 结束语
