一类具有输出时滞的随机系统的H∞保成本控制
2016-09-27何纪
何 纪
(常州信息职业技术学院基础部 江苏常州 213164)
一类具有输出时滞的随机系统的H∞保成本控制
何纪
(常州信息职业技术学院基础部江苏常州213164)
以一类特殊的随机不确定系统为研究对象,系统的状态和控制输出同时具有时滞,综合考虑系统的保成本和H∞控制两种控制方法的优点,研究系统的保成本控制和H∞保成本控制。运用Lyapunov泛函方法,为系统设计了一个有记忆时滞的状态反馈控制器,以LMI的形式给出了状态反馈控制器存在的充分条件,最后,运用数值算例进行验证。
保成本H∞控制; 随机系统; 反馈时滞; 线性矩阵不等式(LMI)
保成本控制的基本思想是,设计控制器,不仅保证闭环系统的稳定性,同时保证由于系统的不确定引起的恶化的二次型性能指标函数有一个确定的上界。文献[1]提出了二次保成本的概念,利用Riccati方程给出了最优二次保成本控制器的设计方法。文献[2]利用LMI的处理方法,对时滞不确定随机系统保成本控制的问题进行了研究。文献[3]研究的是不确定时滞随机系统的最优保成本控制问题;文献[4]研究的是时滞不确定随机系统的保成本控制问题;文献[5]研究的是时滞不确定随机系统的鲁棒H∞保成本控制问题;保成本控制能够使得不确定系统的二次型性能指标具有确定的上界,使得人们在一定程度上了解系统性能的恶化程度。本文以一类特殊的随机不确定系统为研究对象,在系统的状态和控制输出同时具有时滞的情况下,综合系统的保成本和H∞控制两种控制方法的优点,研究系统的保成本控制和H∞保成本控制。
1 问题描述
系统如下状态和输出多时滞不确定随机系统Σ:
dx(t)=[(A+ΔA(t))x(t)+(A1+ΔA1(t))x(t-h)+
(B1+ΔB1(t))u(t)+Bvv(t)]dt+[(E+ΔE(t))x(t)+(E1+ΔE1(t))x(t-h)+
(B2+ΔB2(t))u(t)+Evv(t)]dω(t)
(1)
z(t)=Cx(t)+Du(t)+Gx(t-h)
x(t)=φ(t)∀t∈[-μ,0]
式(1)中u(t)∈Rm为控制输入,z(t)∈Rq为控制输出,x(t)∈Rn为系统的状态变量,v(t)∈Rp为定义在L2[0,∞)上的外部干扰输入,h是常时滞,满足0 MF(t)[HAHA1HEHE1HB1HB2] (2) 其中:HA,HA1,HE,HE1,HB1,HB2,M是已知的实常数矩阵,F(t)∈Rk×l是Lebesgue可测的时变未知矩阵函数,满足 (3) 对于以上系统,构造形式如下的二次型成本指标函数: (4) 其中R1,R2是给定的对称正定加权函数。 定义1:(保成本控制)考虑如(1)式的时滞不确定随机系统Σ,和形如(4)式的闭环成本指标函数,如果存在一个控制律u(t),和一个确定的正数J*,对于系统Σ容许的所有的不确定性,闭环系统是鲁棒均方稳定的,而且闭环成本指标值不超过该确定常数J*,即J≤J*,那么称J*为该系统的一个成本上界,称u(t)为该系统的一个保成本控制器。 考虑有记忆时滞的状态反馈控制器 u(t)=K1x(t)+K2x(t-h) (5) 其中K1,K1是控制器的待定的参数。 定义2:(H∞保成本控制)给出标量γ>0,对不确定随机时滞系统(1)和成本指标函数(4),如果存在一个的控制律u(t),和一个确定的正数J*,对控制系统所容许的所有的不确定性,在不存在外部干扰时,闭环系统是鲁棒稳定的,而且闭环成本指标函数有界(J≤J*),在存在外部干扰v(t)≠0时,闭环系统在干扰抑制度γ下也是鲁棒稳定的,那么,称这样的常数J*为该控制系统的一个成本上限,称这样的控制律u(t)为该控制系统的一个H∞保成本控制器。 对于不确定随机时滞系统Σ(1),考虑有记忆的状态反馈控制器 u(t)=K1x(t)+K2x(t-h) 其中K1,K1是控制器的待定的参数。 ① M<0② A<0,C-BTA-1B<0 ③ C<0,A-BC-1BT<0 引理2[5]:A,D,S,W,F是给定的实矩阵,W>0,FTF≤I,则下列两个结论成立: 1) 对任意向量x,y∈Rn和标量ε>0,有 2xTDFSy≤εxTDDTx+ε-1yTSTSy 2) 对于任意标量ε>0,如果W-εDDT>0成立,有(A+DFS)TW-1(A+DFS)≤AT(W-εDDT)A+ε-1STS 定理1:研究系统(1)(假如v(t)=0),成本指标函数(4),如果可以找到标量ε1>0,ε2>0和矩阵Q>0,X>0,Y1和Y2使得下面的LMI成立: 那么闭环系统是随机保成本可控的。其中保成本控制器为: u(t)=K1x(t)+K2x(t-h) 对应的成本指标函数的上界为: 定理1讨论的是一个不确定随机时滞系统,其状态和输出同时具有时滞,设计了该系统的一个有记忆保成本控制器,给出了使得闭环系统鲁棒稳定的充分条件。特别地,当时滞随机系统不存在不确定项时,以上结果可以变成如下形式: 推论1:考虑系统(Σ),假设v(t)=0,ΔA(t)=0,ΔE(t)=0,ΔA1(t)=0,ΔE1(t)=0,ΔB1(t)=0,ΔB2(t)=0时,如果存在矩阵Q>0,X>0,Y1和Y2使得下面的LMI成立: 那么,可以得到闭环系统是鲁棒随机稳定的。相应的有记忆反馈控制器为 u(t)=K1x(t)+K2x(t-h) 定理2:考虑系统(Σ),对于给定的常数γ>0,如果存在常数标量ε1>0,ε2>0,矩阵Q>0,X>0,Y1和Y2使得下面的LMI成立: 则考虑的系统Σ是鲁棒随机H∞可控的。其中 u(t)=K1x(t)+K2x(t-h) 为保成本控制器,对应的成本指标上界为: 然后,通过Matlab中的LMI工具箱求解线性矩阵不等式可得: ε1=0.365 9,ε2=0.319 5 从而得到H∞线性状态反馈控制器为:u(t)=[9.384 31.491 3]x(t)+[-1.997 710.279 2]x(t-h) 本文以一类状态和控制输出同时具有时滞的随机不确定系统为研究对象,考虑系统的保成本控制和H∞控制。运用Lyapunov泛函方法,为系统设计了一个有记忆时滞的状态反馈控制器,定理1以LMI的形式给出了闭环系统是保成本可控的充分条件;定理2以LMI的形式给出了闭环系统在干扰衰减度γ下是保成本可控的充分条件。最后,运用数值算例进行验证。 [1]Petersen I R, McFarlance D C. Optimal guaranteed cost control and filtering for uncertain linear systems. IEEE Transactions on Automatic Control. 1994(39): 474-484. [2]Yu L, Chu J. LMI approach to guaranteed cost control of linear uncertain time-delay systems. Automatica. 2009(35): 1155-1159. [3]Li H, Niculescu S I, Dugard L, Dion J M. Robust guaranteed cost control of uncertain linear time-delay systems using dynamic output feedback. Mathematics and Computers in Simulation. 1998(45): 349-358. [4]Zhou K et al. Robust performance of systems with structured uncertainties in state space. Automatica. 1995(31): 249-255. [5]Xu S Y, Lam J, Yang C W, Verriest E I. An LMI approach to guaranteed cost control for uncertain linear neutral delay systems. International Jounal of Robust and Nonlinear Control. 2010(13):35-55. Robust H∞Guaranteed Cost Control for Stochastic Systems with Output-Delay HE Ji (Dept. of Basic Courses, Changzhou College of Information Technology, Changzhou 213164, China) With consideration of a kind of robust H∞guaranteed cost control for stochastic systems with state and output-delays, this paper focuses on the design of a linear state feedback controller which ensures the closed-loop system to be mean-square asymptotically stable. A sufficient condition of this problem is given by a linear matrix inequality(LMI). Finally it provides an example to show the effectiveness of the proposed method. robust H∞guaranteed costcontrol; stochastic systems output-delay; linear matrix inequalities(LMI) 2016-04-25 何纪(1982-),男,讲师,硕士,主要研究方向:控制理论与控制工程 O 231 A 1672-2434(2016)04-0026-03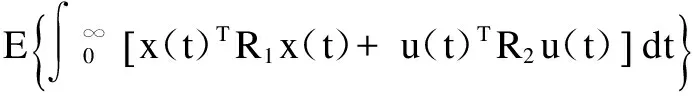
2 具有输出时滞的随机系统的保成本控制
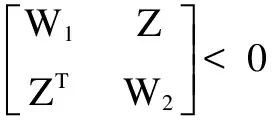

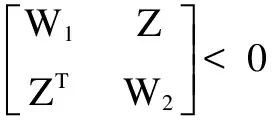
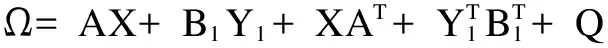
3 具有输出时滞的随机系统的H∞保成本控制
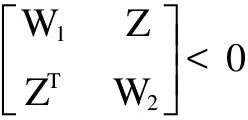
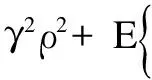
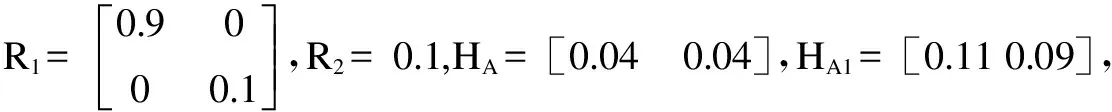
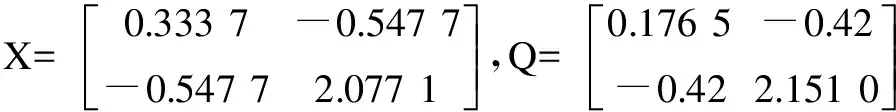
5 结束语
