1954—2013年榆林极端气温变化趋势及周期振荡特征

刘宇峰，郭玲霞，原志华，吴　林

（1.咸阳师范学院 a.资源环境与历史文化学院，b.经济与管理学院，陕西 咸阳 712000；2.中国科学院遗传与发育生物学研究所 农业资源研究中心，河北 石家庄 050021）

［区域经济与资源环境可持续发展研究］

1954—2013年榆林极端气温变化趋势及周期振荡特征

刘宇峰1a，郭玲霞1a，原志华1b，吴林2

（1.咸阳师范学院 a.资源环境与历史文化学院，b.经济与管理学院，陕西 咸阳 712000；2.中国科学院遗传与发育生物学研究所 农业资源研究中心，河北 石家庄 050021）

基于榆林1954—2013年逐日气温资料，辅以线性趋势、累积距平、Morlet小波分析等方法，分析榆林近60 a极端气温的变化趋势及周期振荡特征。结果表明：（1）极端气温极值指数（TXx和TNn）总体呈现上升趋势，且TXx经历了“下降—上升—下降—上升—下降”5个阶段的波动变化，而TNn具有波动下降和波动上升2个变化阶段。（2）极端暖指数（SU）为不显著的增加趋势，且经历了3次波动变化；极端冷指数（ID、FD）表现出显著的减少趋势，其中ID以分为波动上升、下降、上升3个变化阶段，FD则分为剧烈波动上升和剧烈波动下降阶段2个阶段。（3）极端暖指数（TX90、TN90）总体表现出显著的上升趋势，极端冷指数（TX10、TN10）则为显著的下降趋势；4种极端气温相对指数总体上均经历了2个变化阶段。（4）所有极端气温指数时间序列在近60 a均存在多时间尺度特征，其中TXx和TNn的第一主周期分别是31 a和22 a，SU、ID和FD的第一主周期分别是30 a、30 a和23 a，TX90、TX10、TN90、TN10的第一主周期分别是31 a、30 a、23 a和11 a。

极端气温；Morlet小波分析；累积距平；榆林

全球气候变化是当前世界各国面临的一项巨大挑战，气候变化给人类社会带来的威胁无疑是当前风险社会时代最突出的风险之一。据联合国政府间气候变化专门委员会（IPCC）第五次评估报告指出，全球气候系统变暖已成为不争的事实，1951—2012年全球平均气温升高了0.72℃［1］。气候变暖使高温、干旱、暴雨、洪涝等极端气候事件在时空分布上发生显著变化，尤其是在对气候变化异常敏感的区域或生态环境脆弱区。极端气候事件对人类社会的影响是全方位、多层次和多尺度的，尤其是极端气候事件的发生对农业和粮食安全、生态环境安全、水资源安全等都产生了重大而深远的影响。

因此，在全球气候变暖的背景下，极端气候的研究受到众多学者的普遍关注。任国玉［2］等对近年来中国极端气候变化的研究成果进行了系统梳理和总结，指出1951年以来中国大陆地区极端气候事件频率和强度发生了一定变化，但不同类型和不同区域极端气候变化存在明显差异；王晓［3］等基于1960—2011年31个气象站点的气温资料，选取8个极端气温指数对云南省极端气温事件的时空变化及周期特征进行了研究，得出云南极端气候事件呈现整体上升的结论；李芬［4］等利用62个气象站点1961—2010年的逐日最低地温资料，分析了山西终霜冻的时空分布特征，认为山西的终霜冻日总体上呈现南部早北部晚的特点，但具体分布还受地形和地理位置的影响；王琼［5］等根据1962—2011年长江流域115个气象站点的逐日最高气温、日最低气温资料，选取16个极端气温植被分析了长江流域极端气温的时间变化趋势和空间分布规律，结果表明极端冷指数的线性变化呈下降趋势，而极端暖指数的线性变化呈上升趋势，且各个指数的空间分布差异显著；赵雪雁［6］等选取11个极端气温指数分析了1963—2012年青藏高原东缘极端气温的变化趋势，结果显示极值指数、极端暖指数及生物生长季呈上升趋势，而极端冷指数及气温日较差呈下降趋势。此外，许多学者还对中国其他地区的极端气温进行了研究［7-9］。总的来看，目前国内对极端气温的研究主要以大区域（流域）为尺度，而对县（市）级尺度下的极端气温研究还比较匮乏。

榆林市位于陕西省的最北部，地处陕北黄土高原和毛乌素沙地交界处，是黄土高原与内蒙古高原的过渡区，生态环境极其脆弱，成为众多学者研究气候变化的理想区域。研究榆林在全球气候变化背景下的气候变化规律，有助于深刻理解和认识整个毛乌素沙地乃至更大区域的气候变化特征，对区域气象灾害的减防及经济社会的可持续发展具有重要意义。基于此，本文以榆林为例，研究其过去60 a极端气温的变化趋势及周期振荡特征。

1　资料与方法

1.1数据来源

本文利用中国气象科学数据共享服务网（http:// cdc.cma.gov.cn）中地面日值数据集榆林站1954—2013年的逐日最高气温和最低气温进行整理、计算得到各种极端气温指数。对个别缺测数据采用线性插值及平均值等方法进行插补［6］。

1.2研究方法

1.2.1极端气温指数定义及计算

本研究极端气温指数的选取参考世界气象组织（WMO）气候委员会（CCI）在气候变化监测会议中确定的“气候变化检测和指标”（Expert Team on Climate Change Detection and Indices）建议标准［10-11］。本文共选取9个极端气温指标，分为3种类型，具体见表1。

极端气温相对指数的计算采用国际上常用的百分位阈值法。例如，将榆林站1954—2013年中同日的最高/最低气温资料按照升序进行排列，将该日第90（10）个最高/最低气温的百分位值作为极端气温的阈值，由此可得到365个（闰年为366个）最高/最低气温的第90（10）个百分位值，当某日的最高气温大于第90个百分位值，说明该日出现极端高温事件，如果某日的最低气温小于第10个百分位值，则说明该日出现了极端低温事件。百分位值的具体计算过程参见文献［12］。

1.2.2气候变化倾向率

将气候要素写成随时间变化的一次直线方程，一般地，其直线斜率的10倍表示气候变化倾向率。函数表达式如下［13］：

式中t为时间，a，b分别为回归系数和回归常数，可用最小二乘法求得，a的10倍为气候变化倾向率，a值的正负反映y的变化趋势，正值表示上升趋势，反之亦然。

1.2.3累积距平

累积距平是一种常用的、由曲线直观判断变化趋势的方法。

表1　极端气温指数

1.2.4Morlet小波分析

在分析具有多尺度、多层次、多分辨率变化特性的时间序列时，小波分析是一种有效的工具，它可以同时在时域和频域上揭示信号的细微变化［14］。本文利用Morlet连续复小波变换来分析极端气温事件变化的周期性，小波变换［15-18］的具体原理见参考文献。在进行分析时，先将数据序列两端进行延伸以消除“边界效应”，然后再进行小波变换。通过小波变换可得到小波变换系数，去除延伸数据保留原始数据，进而绘制小波系数实部等值线图。正的小波系数对应偏高（多）期，负的小波系数对应偏低（少）期，小波系数为零对应着突变点；小波系数的绝对值越大，说明气候要素在该时间尺度变化越显著。此外，利用小波方差对时间序列的主要周期进行检验，小波方差图可反映气候要素在不同时间尺度周期波动的强弱，小波方差在某一时间尺度上的极值对应该尺度上的显著周期。

2　极端气温指数的趋势变化

采用线性变化倾向率来描述极端气温指数的总体变化趋势，利用累积距平法分析时间序列的阶段性特征，同时计算极端气温指数时间序列的标准差，以1个标准差为标准，选择大于（小于）标准差正值（标准差负值）的年份为极端气温指数异常偏高/低（多/少）年（图1）。

2.1极端气温极值指数变化

近60 a来，极端气温极值指数TXx（年内日最高气温）和TNn（年内日最低气温）总体呈现上升趋势［图1（a）、图1（b）］，两者的变化幅度分别在32.7～39.0℃和-32.7～-19.2℃之间，变化倾向率分别是0.07℃/10a（相关系数|R|=0.095＜R0.1=0.211，未通过显著性检验）和0.36℃/10 a（相关系数|R|= 0.224＞R0.1=0.211，通过显著性检验），由此来看，TNn的增温趋势要强于TXx。从累积距平曲线来看，TXx变化大致分为5个阶段，即在1954—1964、1965—1976、1977—1994、1995—2010和2011—2013年经历了“下降—上升—下降—上升—下降”的波动变化，其中1960、1961、1966、1997、1999、2000、2001、2005和2010年为异常偏高年份，而1956、1962、1964、1977、1988、1989、1993、2012和2013年为异常偏低年份；TNn变化分为2个阶段：1954—1971年为波动下降期，1972—2013年为波动上升期，其中1961、1979、1987、1990、1994、1995、2007年是异常偏高年，而1954、1955、1956、1963、1971、1978、1984、1991、1993、1998、2002和2008年则为异常偏低年。

2.2极端气温绝对指数变化

极端气温绝对指数（夏日日数SU、结冰日数ID和霜冻日数FD）的冷暖指数在近60 a表现出完全相反的变化趋势［图1（c）、图1（d）、图1（e）］，其中极端暖指数（SU）整体为增加趋势，变化倾向率为0.68 d/10 a（相关系数|R|=0.118＜R0.1=0.211，未通过显著性检验），变化幅度在80～126 d之间；极端冷指数（ID、FD）总体表现出减少趋势，变化倾向率分别是-2.72 d/10 a（相关系数|R|=0.369＞R0.1=0.211，通过显著性检验）、-2.99 d/10 a（相关系数|R|=0.500＞R0.1= 0.211，通过显著性检验），变化幅度分别在15～76 d 和130～172 d之间；极端冷指数的减少趋势与极端暖指数的增加趋势相比更加显著。累积距平变化曲线显示，SU总体上经历了下降、上升、下降的波动变化趋势，持续时间分别是32 a（1954—1985）、20 a （1986—2005）和8 a（2006—2013），其中有11 a属异常偏多年份，尤其是1987和1998年，均达到最大正距平（23 d），有7 a为异常偏少年份，1976年达到最大负距平（-23 d）；ID以1986和2004年为转折点分为3个变化阶段，即1954—1986、1987—2004和2005—2013年分别为波动上升、下降、上升趋势，其中异常偏多（12 a）和偏少（9 a）年份均较多，异常偏多年主要集中在20世纪60年代初期至70年代初期，而异常偏少年主要集中在20世纪80年代末期至21世纪初期；FD以1995年为转折点分为2个明显的变化阶段，1954—1995年为剧烈波动上升阶段，正距平年份比例达76%，说明这42 a中绝大多数年份的FD多于多年平均值，1996—2013年为剧烈波动下降阶段，FD以11.61 d/10 a的速率在减少，除2000、2002 和2012年的距平为正值外，其余年份的距平值均为负，尤其是2007年达到最大负距平（-23 d）。

图1　1954—2013年榆林极端气温的时间变化趋势

2.3极端气温相对指数变化

极端气温相对指数（暖昼TX90、冷昼TX10和暖夜TN90、冷夜TN10）的冷暖指数亦表现出相反的变化趋势［图1（f）、图1（g）、图1（h）、图1（i）］，其中极端暖指数（TX90、TN90）总体上均表现出显著的上升趋势，变化倾向率分别为3.69 d/10 a（相关系数|R|= 0.321＞R0.1=0.211，通过显著性检验）和6.69 d/10 a（相关系数|R|=0.601＞R0.1=0.211，通过显著性检验），两者的变化幅度分别在7～99 d、14～100 d之间；极端冷指数（TX10、TN10）整体上呈现出显著的下降趋势，变化倾向率分别为-2.22 d/10 a（相关系数|R|=0.341＞R0.1=0.211，通过显著性检验）和-6.07 d/10 a（相关系数|R|=0.595＞R0.1=0.211，通过显著性检验），两者的变化幅度分别在16～66 d、8～78 d之间；从极端气温相对指数变化趋势的相对显著性来看，TN90和TN10的变化趋势要显著于TX90和TX10，TX10的下降趋势显著于TX90的上升趋势，TN90的上升趋势显著于TN10的下降趋势。由累积距平曲线可知，4种极端气温相对指数总体上均经历了2个变化阶段，其中TX90累积距平在1986年以前为波动下降趋势，1986年以后为波动上升趋势，但在1987—1996年和2003—2013年两个阶段变化相对较平稳且在2011—2013年出现短期下降趋势，TX90存在7 a的异常偏多年和4 a的异常偏少年，异常偏多年份主要集中在20世纪80年代末期至21世纪初期，异常偏少年份为1964、1976、2011和2012年；TX10累积距平变化亦以1986年为转折点分为前期波动上升后期波动下降2个阶段，其中在1954—1966年和2002—2013年2个阶段变化较平稳，TX10异常偏多年有9 a且主要集中在1956—1976年，异常偏少年有11 a且主要集中在1994—2001年；TN90累积距平在1954—1996年为剧烈下降趋势，此阶段绝大多数年份（占90%）的距平值为负，1997—2013年为剧烈上升趋势，此阶段除2012年为负距平外，其他年份均为正距平，TN90有12 a异常偏多且全部集中在1998—2013年，有7 a异常偏少且主要集中在1980—1988年；TN10累积距平以1993年为转折点分为2个变化阶段，表现为1954—1993年的剧烈波动上升和1994—2013年的剧烈波动下降，其中波动上升期的绝大多数年份（占68%）为正距平，而波动下降期的所有年份均为负距平，TN10有13 a为异常偏多年且主要集中在1962—1976年，有11 a为异常偏少年且全部集中在1999—2013年。

3　极端气温指数的周期振荡特征

3.1极端气温极值指数周期变化

极端气温极值指数（TXx和TNn）时间序列在过去60 a的变化过程中存在多时间尺度特征，大尺度变化中嵌套着复杂的小尺度结构［图2（a）、图2 （b）］。TXx主要存在着6～9 a和29～31 a的时间尺度，在6～9 a尺度上，存在多个周期振荡中心且贯穿了整个研究时域；在29～31 a尺度上，出现较6个明显的高、低振荡中心，高振荡中心对应年份大致是1961、1980和1999年，低振荡中心年份为1971、1991 和2012年，由于最后一个低振荡区域等值线并未完全封闭，预示着榆林TXx在未来短时间尺度上仍然偏低。TNn存在3～6 a、9～11 a、15～19 a和21～23 a的时间尺度，在3～6 a尺度上，周期振荡不具全域性，主要发生在21世纪60年代以及80年代以后；9～11 a尺度上的周期振荡在21世纪70年代以后表现得最为明显，且振荡中心在20世纪90年代以后下移，周期缩短；15～19 a尺度的周期变化不明显且主要发生在21世纪90年代中期以后；在21～23 a尺度上，周期振荡明显且具有全域性，出现较完整的8个高、低振荡中心，说明TNn在过去60 a经历了4次“低—高”循环，最后一个高振荡区域在2011年已完全形成，且在2011年以后已出现低值等值线，反映年内日最低气温在未来有偏低倾向。从极端气温极值指数的小波方差变化来看（图3），TXx和TNn分别出现2个和4个极值，从极值大小判断TXx的第一主周期是31 a，其次是9 a；TNn的第一主周期是22 a，其次是19 a、9a和3 a。

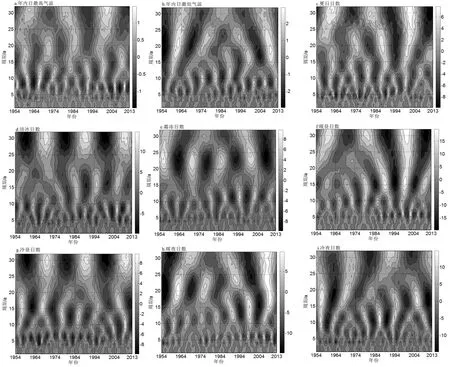
图2　1954—2013年榆林极端气温指数周期变化

3.2极端气温绝对指数周期变化

极端气温绝对指数周期变化（SU、ID和FD）见图2（c）、图2（d）和图2（e）。由图可知，SU主要存在5～10 a、14～17 a、20～22 a和29～31 a的周期变化，其中5～10 a和29～31 a尺度上的周期振荡几乎贯穿整个研究时域，具体表现为5～10 a尺度上的多个正负位相交替及29～31 a尺度上的6次正负循环，同时我们看到29～31 a尺度上的最后一个负振荡中心并未完全形成，预示着SU在未来将继续偏少；14～17 a和20～22 a两种时间尺度的周期变化时有时无，前者主要集中在21世纪60年代至70年代中期以及2004年以后，后者则主要集中在21世纪70年代至2004年。ID具有6～8 a、15～16 a和29～30 a 3种时间尺度的周期变化，在6～8 a尺度上，结冰日数具有多个“偏多—偏少”循环交替，振荡中心对应时间尺度在20世纪60年代中期以前在8 a左右，以后逐渐下移到6 a左右且一直持续到80年代中期，然后又逐渐上移到8 a左右且持续到2013年；在15～16 a尺度上，周期振荡在20世纪80年代中期以前并不明显，而主要发生在80年代中期以后；29～30 a尺度上的周期振荡非常强烈且贯穿整个时域，出现6个完整的正负振荡中心，反映ID在近60 a经历了“偏少—偏多—偏少—偏多—偏少—偏多”3次周期循环，且每次循时间环持续约20 a，最后一个正振荡区已基本形成，则未来ID可能偏少，进入新一轮周期循环。FD具有4～6 a、9～12 a和23～24 a 3种时间尺度，4～6 a短尺度上的周期振荡不明显，9～12 a中尺度上的周期振荡较明显，其振荡中心对应时间尺度在20世纪80年代以前较小（9 a左右），而80年代以后逐渐上移，尺度变为12 a左右；23～24 a大尺度上的周期振荡很明显，存在8次正负交替，即4次“偏多—偏少”周期循环，最后一个周期循环大致在2011年左右结束，同时出现高值等值线，揭示FD在2011年以后的短时间尺度上继续偏多。小波方差图显示SU、ID和FD均存在多个尺度的周期振荡（图3），但它们的第一主周期分别是30 a、30 a 和23 a。

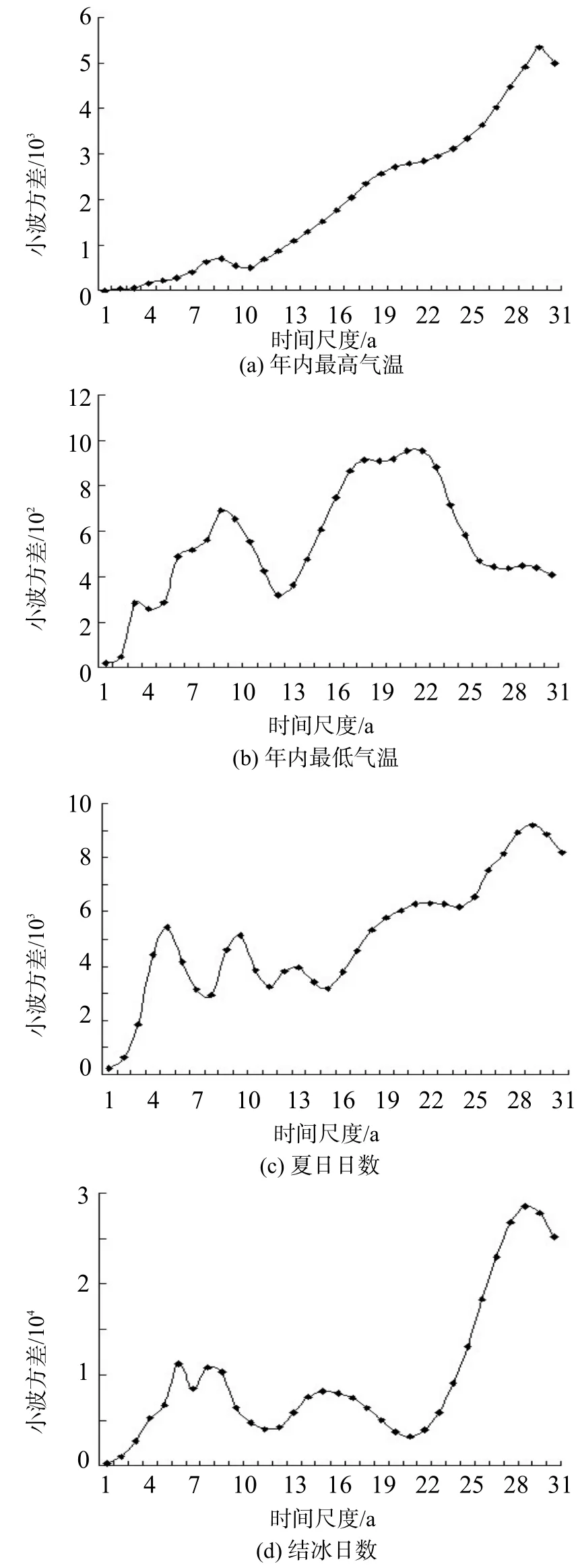
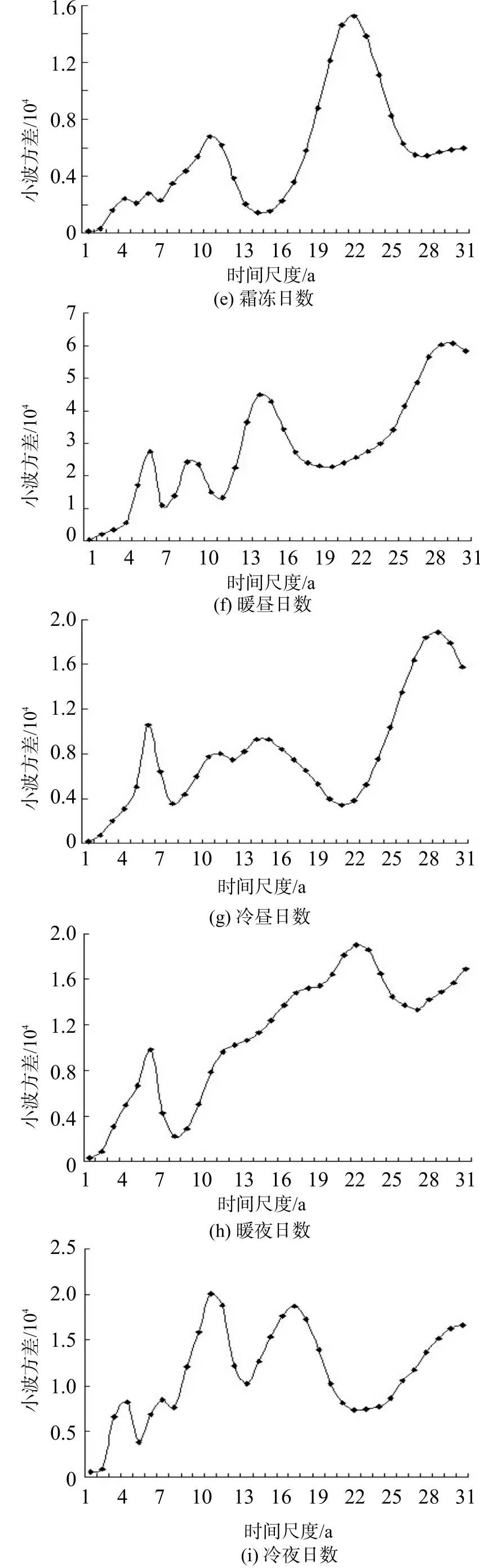
图3　榆林极端气温指数小波方差

3.3极端气温相对指数周期变化

极端气温相对指数（TX90、TX10、TN90、TN10）周期变化见图2（f）、图2（g）、图2（h）和图2（i）。TX90存在5～7 a、8～10 a、14～15 a和30～31 a的周期变化，其中14～15 a和30～31 a尺度上的周期振荡较强，尤其是30～31 a尺度的周期振荡具有明显的全域性，出现3次较完整的“偏多—偏少”交替循环，且最后一个负振荡中心已经闭合，说明TX90在未来将进入新一轮的“偏多—偏少”循环；14～15 a的振荡主要发生在20世纪80年代之后；8～10 a的振荡亦具有全域性但并不强烈，5～7 a的振荡主要发生在20世纪90年代之后。TX10具有5～7 a、9～12 a、15～16 a和29～31 a四种尺度的周期振荡，其中9～12 a和15～16 a尺度在不同时期进行切换，20世纪70年代之前振荡周期为15～16 a，70年代至90年代末期振荡周期为9～12 a，90年代末期以后振荡周期又延长到15～16 a；5～7 a的振荡主要发生在20世纪各年代；29～31 a的振荡在整个时段上表现的最强烈，具有完整的“偏少—偏多”3次循环，且最后一个正振荡中心已经形成，反映未来的TX10在短期内将表现出偏少状态。TN90在5～6 a、10～15 a和20～23 a尺度上存在周期振荡，其中5～6 a尺度上的振荡主要集中在20世纪70年代中期以后，10～15 a尺度上的振荡自1954年开始表现出逐渐延长的趋势，即周期从10 a逐渐增加到15 a，20～23 a尺度上的振荡最强烈，且随着时间的推移同样呈现除逐渐延长的趋势，在整个研究时段上经历了较完整的4次“偏少—偏多”循环，最后一个正振荡中心已经闭合，说明未来TN90在短期内会出现偏少的状况。TN10同样具有3～5 a、7～8 a、10～12 a、17～18 a的周期振荡特征，其中短时间尺度3～5 a、7～8 a的周期变化并不明显，10～12 a的周期振荡贯穿整个时域，出现完整的7次“偏多—偏少”循环及不完整的1次“偏多—偏少”交替，最后一个负振荡中心并未闭合，表明TN10将继续偏少，17～18 a的周期变化也相对较强，在整个时域上经历了较完整的5次“偏多—偏少”循环。小波方差图显示TX90、TX10、TN90、TN10均存在多个尺度的周期振荡（图3），且它们的第一主周期分别是31 a、30 a、23 a和11 a。

4　结论

本文基于榆林1954—2013年逐日平均气温数据，采用气候倾向、累积距平、标准差、Morlet小波分析等方法，分析了该地区极端气温指数的趋势变化及周期振荡特征，得出以下主要结论：

（1）极端气温极值指数（TXx和TNn）总体呈现上升趋势，但TXx的变化趋势不显著而TNn的变化趋势显著，且TNn的增温趋势要强于TXx；TXx在近60 a经历了“下降—上升—下降—上升—下降”5个阶段的波动变化，而TNn则经历了波动下降和波动上升2个变化阶段。

（2）极端气温绝对指数（SU、ID和FD）的冷暖指数在近60 a表现出完全相反的变化趋势，其中极端暖指数（SU）为不显著的增加趋势，且经历了下降、上升、下降的波动变化趋势；极端冷指数（ID、FD）总体表现出显著的减少趋势，ID以1986和2004年为转折点分为波动上升、下降、上升3个变化阶段，FD则以1995年为转折点分为剧烈波动上升和剧烈波动下降阶段2个明显的变化阶段。

（3）极端气温相对指数（TX90、TX10、TN90、TN10）的冷暖指数亦表现出相反的变化趋势，其中极端暖指数（TX90、TN90）总体上均表现出显著的上升趋势，极端冷指数（TX10、TN10）整体上呈现出显著的下降趋势；4种极端气温相对指数总体上均经历了2个变化阶段，其中TX90和TX10在1986年前后分别为波动下降和波动上升趋势，TN90以1996年为转折点，经历了先剧烈下降后剧烈上升的变化趋势，TN10以1993年为转折点先后经历剧烈波动上升和剧烈波动下降2个阶段。

（4）在周期变化上，所有极端气温指数时间序列在近60 a均存在多时间尺度特征，大尺度变化中嵌套着复杂的小尺度结构，其中极端气温极值指数TXx和TNn的第一主周期分别是31 a和22 a，极端气温绝对指数SU、ID和FD的第一主周期分别是30 a、30 a和23 a，极端气温相对指数TX90、TX10、TN90、TN10的第一主周期分别是31 a、30 a、23 a和11 a。

［1］IPCC.Climate Change 2013：The physical science basis，the summary for policymakers of the working group i contribution to the fifth assessment report［M］.New York:Cambridge University Press，2013.

［2］任国玉，封国林，严中伟.中国极端气候变化观测研究回顾与展望［J］.气候与环境研究，2010，15（4）：337-352.

［3］王晓，李佳秀，石红彦，等.1960—2011年云南省极端气温事件的时空分布及趋势预测［J］.资源科学，2014，36（9）：1816-1824.

［4］李芬，张建新，武永丽，等.近50年山西终霜冻的时空分布及其影响因素［J］.地理学报，2013，68（11）：1472-1480.

［5］王琼，张明军，王圣杰，等.1962—2011年长江流域极端气温事件分析［J］.地理学报，2013，68（5）：611-625.

［6］赵雪雁，雒丽，王亚茹，等.1963—2012年青藏高原东缘极端气温变化特征及趋势［J］.资源科学，2014，36（10）：2113-2122.

［7］李玲萍，薛新玲，李岩瑛，等.1961—2005年河西走廊东部极端气温事件变化［J］.冰川冻土，2010，32（1）：43-51.

［8］陈晓光，Declan C，郑光芬，等.1961—2004年宁夏极端气温变化趋势分析［J］.气候变化研究进展，2008，4（2）：73-77.

［9］马晓华，赵景波.1958—2013年豫南地区极端气温变化特征及周期分析［J］.资源科学，2014，36（9）：1825-1833.

［10］VINCENT LA，PETERSON T C，BARROS V R，et al.Observed trends in indices of daily temperature extremes in South American1960—2000［J］.Journal of Climate，2005，18：5011-5023.

［11］AGUILAR E，PETERSON T C，OBANDO P R，et al. Changes in precipitation and temperature extremes in Central America and northern South America，1961—2003［J］. Journal of Geophysical Research，2005，110：D23107，DOI：10.1029/2005J D006119.

［12］BONSAL B R，ZHANG X B，VINEENT LA，et al.Characteristics of daily and extreme temperature over Canada［J］. Journal of Climate，2001，5（14）：1959-1976.

［13］魏凤英.现代气候统计诊断与预测技术［M］.北京：气象出版社，2013：37-69.

［14］徐建华.现代地理学中的数学方法［M］.北京：高等教育出版社，2002.

［15］马翠丽.基于小波分析的长江入河口区水沙通量变异规律研究［D］.上海：华东师范大学，2006.

［16］王红瑞，叶乐天，刘昌明，等.水文序列小波周期分析中存在的问题及改进方法［J］.自然科学进展，2006，16（8）：1002-1007.

［17］XU Y Q，LI S C，CAI Y L.Wavelet analysis of rainfall variation in the Hebei Plain［J］.Science in China（Series D:Earth Science），2005，48（12）：2241-2250.

［18］杨志峰，李春晖.黄河流域天然径流量突变性与周期特征［J］.山地学报，2004，22（2）：140-146.

Analysis of Extreme Temperature Events and Its Period in Yulin During 1954-2013

LIU Yufeng1a，GUO Lingxia1a，YUAN Zhihua1b，WU Lin2
（1.a.College of Resources and Environment&History and Culture，b.College of Economics and Management，Xianyang Normal University，Xianyang 712000，Shaanxi，China；2.The Center forAgricultural Resources Research，Institute of Genetics and Developmental Biology of Chinese Geographical Sciences，Shijiazhuang 050021，Hebei，China）

This article aims to analyze the change of extreme temperatures and its cycles in Yulin of Shaanxi Province from 1954 to 2013.The daily data from 1954 to 2013 in Yulin is collected to analyze the temporal change of extreme temperatures and its cycles by using the methods of humidity index，Morlet complex wavelet and so on.The results show that:a）The TXx and TNn were increasing in fluctuation and there were five obvious fluctuation changes for TXx but two for TNn during 1954-2013.b）The SU had no significant change trend which experienced three fluctuation changes，while ID and FD exhibited obvious decrease tendencies.The TX90 and TN90 showed significant increasing trends while the TX10 and TN10 reduced significantly.There were two obvious stages variety characteristic for TX90，TN90，TX10 and TN10 periodic oscillation with multiple time scales of extreme temperature index in Yulin in which the first major cycles of TXx，TNn，SU，ID，FD，TX90，TX10，TN90，TN10 respectively were 31 a，22 a，30 a，30 a，23 a，31 a，30 a，23 a and 11 a.

extreme temperatures；Morlet complex wavelet；accumulative anomalies；Yulin

P46

A

1672-2914（2016）04-0071-08

2016-03-15

陕西省教育厅科研基金项目（16JK1828）；陕西省普通高等学校优势学科建设项目（历史地理学0602）；咸阳师范学院科研基金项目（12XSYK032）。

刘宇峰（1981—），男，山西忻州市人，咸阳师范学院资源环境与历史文化学院讲师，博士，研究方向为区域环境演变。