明末清初太阳视差在中国的传播

张　祺,宋芝业

(内蒙古师范大学 科学技术史研究院,内蒙古 呼和浩特　010022)



明末清初太阳视差在中国的传播

张祺,宋芝业

(内蒙古师范大学 科学技术史研究院,内蒙古 呼和浩特010022)

明末清初之际，太阳视差传入中国,并被积极引入官方历法。从《崇祯历书》到《历象考成后编》均对其进行了不同程度的整理与修正,理论层面上已经与西方相差不远,但由于中国天文学以实用为中心的价值取向,仅将其作为历法计算的重要参数,未能产生类似于西方的影响。通过对比几部官方历法中太阳视差的相关记述,研究清代历算家对该项知识的3次主要修改,并在此基础上分析清代历算家对太阳视差的认识程度以及科学诉求。关键词：视差;天文单位;历法

太阳视差又称太阳赤道地平视差,在雷达天文学问世之前,地月系质心到太阳的距离,即天文单位,皆需通过太阳视差测定。近几个世纪以来,太阳视差一直是天文学的重要问题。1672年火星冲日期间,卡西尼及其助手通过观测数据推算出了当时最为精确的太阳视差,将原先的日地距离扩大了近20倍,引起西方学术界极大的轰动。1738年《历象考成后编》编撰时,将卡西尼的观测数据及推算方法收入其中,但却并没有产生类似西方的轰动效应。本文基于原始文献,通过比对明末清初直至乾嘉时代的几部官方历法著作,分析当时学者对太阳视差的理解方式,进而了解中国历算家对太阳视差的认识程度以及科学诉求。

1　《崇祯历书》中的太阳视差

最早传入中国的西方视差知识,见于1605年由利玛窦(Matteo Ricci,1552—1610)与李之藻(1565—1630)合译的《乾坤体义》。该书主要介绍地圆说、地球五带划分、行星内外顺序等西学基础知识。文中讨论“日球大于地球,地球大于月球”时绘有一图,名为“测量月离地几何式”,其中就包含一些地平视差知识。

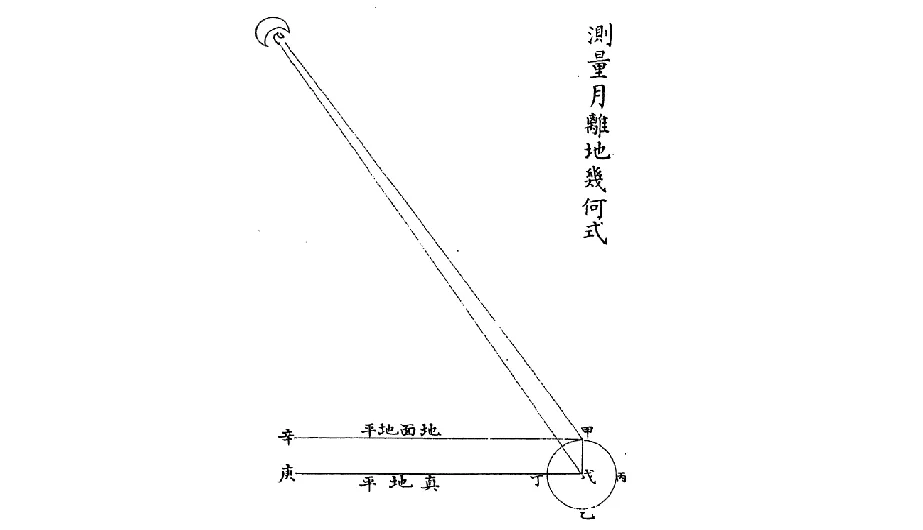
图1　《乾坤体义》中的月地距离计算模型Fig.1　Calculation model of the distance between Month and Earth

假如甲乙丙丁为地球,戊为其心,甲戊为地球半径,己为月,戊庚真地平,甲辛地面地平也。从甲地面欲测己戊线,乃月离地心里数之几何矣[1]。

这是一段介绍月地距离计算方法的文字,后文具体算法中先后用到了“真地平高度”与“视地平高度”,并指明它们之间的差异,该差异其实就是地平视差。文中虽未明确使用这一概念,但已经相当于用地平视差求解月地距离。

1607年,李之藻与利玛窦合译的实用天文学著作《浑盖通宪图说》出版,其中的“地平规说”再次提及地平视差的相关知识。

此规应设二规,一当地中半处,一当地面。若太阳、金星及木、火、土三星离地绝远,即以地中做平规,算法亦无差。若算太阴及金、水二星,离地不甚远,则当就地面起算,方得确度耳[2]。

文中主要介绍地平规的用法,主张将行星的地平视差按距离分为两类,其中月亮、金星、水星离地心较近,视差较大。而太阳、土、木、火三星及恒星离地较远,视差微乎其微,可忽略不计。

1612年,王英明《历体略》刊出,该书主要是一部介绍中西天文学的通俗性著作。书中关于地平视差亦有所涉及,但内容与之前著作大同小异,如其言道:

太阳当空,列曜俱熄,至夜而星可测也。星莫灿于五纬,然各有迟留退伏。又金、水、太阴距地最近,不可以地面为较。自太阳以上,诸曜距地绝远,则地面、地心总之不异[3]。

明末清初之际的天文历法著作中,介绍地平视差最为全面、理论最为系统的,当推徐光启(1562—1633)率同汤若望(Johann Adam Schall von Bell,1591—1666)、罗雅谷(Giacomo Rho,1593—1638)等传教士编撰的《崇祯历书》。入清以后,该书又由汤若望等人略加删改,更名为《西洋新法历书》。《崇祯历书》成书于1634年,书中对日、月、五星地平视差的概念、几何原理、观测中的作用、《地半径差表》的构造方法都做出了较为详细的论述。特别值得注意的是,修改了之前著作中无需考虑太阳视差的说法,对这一问题给予了足够的重视。如《崇祯历书·日躔历指》开篇即批评古法测冬、夏至日高时,未考虑到“人目不在地心在地面,故得数未确。”[4]相对于中国传统测量方法及早期的西学普及性著作,可说是一个较大的变化。

关于太阳视差的几何原理及观测中的作用,《崇祯历书》主要通过作图明之:

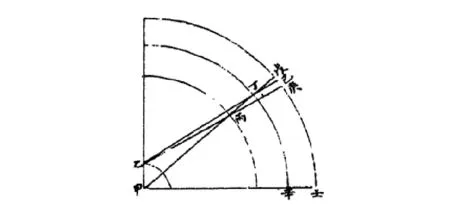
图2　《崇祯历书》中的地平视差Fig.2　The horizontal parallax in "Chong Zhen Li Shu"

如上图,甲为地心,甲乙为地半径,丁辛为日躔最高圈,日行在最高丁,人见日躔于外天巳,壬巳弧为其地平上之视高。然从地心测之,则壬戊为其地平上之实高,两高之差为戊丁巳角或乙丁甲角。若日行高冲丙,从地心测其实高仍在戊,与在最高丁等,则从地面乙视之,见日躔于外天庚……故太阳之实高等,随时所见视高不等,其视差之数亦不等[4]。

《崇祯历书》通过作图说明了太阳视差的几何意义,可视为明末清初以来最为详细的介绍。除作图说明外,《崇祯历书》较大的亮点是给出了《地半径差表》及其造表法,具体流程主要分为两步:

步骤一:在偏心圆模型下求得日地的距离

如图3:丙为地心,戊为太阳位置,乙为太阳本天心,乙丙为两心差e=358416,甲戊弧为太阳平行度M0、甲乙为太阳本天半径R1=10000000。通过模型的几何推导,求得日地距离为:

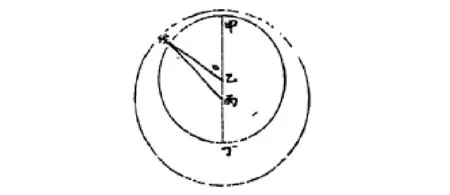
图3　《崇祯历书》中的太阳运动模型Fig.3　The model of sun′s motion in "Chong Zhen Li Shu"

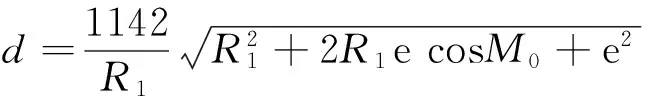
在求解过程中,《崇祯历书》预先设定地球半径与太阳本天半径之比例为1∶1142,该数据引自哥白尼《天体运行论》,但本身误差较大,这也就成了太阳视差数值偏大的主要原因。

步骤二:求解太阳视差

如图4:丙为地心,丁为地面,乙为太阳,则甲乙为太阳天顶距z1,乙角即为地半径差p,则有:

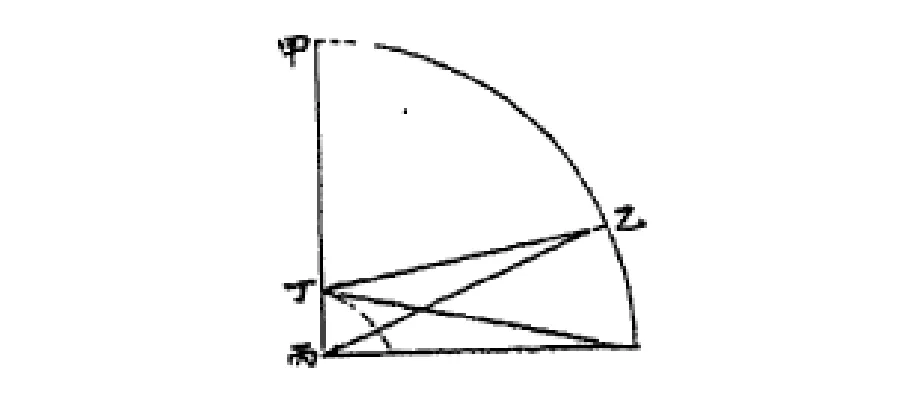
图4　《崇祯历书》中的视差模型Fig.4　The model of parallax in "Chong Zhen Li Shu"

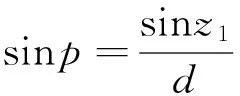
其中p即为太阳在该位置处的视差。

《崇祯历书》解释了太阳视差的计算原理,但模型中一些常数的求解方法却并未交待,理论上仍有混乱之处。具体造表时,只依据模型数据选取近地点、远地点、中间点三段距离列表。若太阳处于其他位置,则依据“夏至左右三宫属最高,春秋分各左右三宫属中距,冬至左右三宫属最高冲”[4]的原则选取表中数据。但如此一来,造表法中求解日地距离d的步骤似乎又显得多余了。《历象考成》重编《地半径差表》时,虽模仿《崇祯历书》以近、远、中三位置列表,但各位置的日地距离却采用国内观测数据重新计算,逻辑上更合理一些。

2　《历象考成》中的太阳视差

1635年《崇祯历书》编成后,就不断遭到保守派的激烈反对,直至1644年明朝灭亡,始终未能颁行[5]。其修改本《西洋新法历书》由于时间仓促,书中依然存在着诸如图表不和、各种天文理论之间较为杂乱等不足之处,后虽经南怀仁等人几次修订,但情况并未改观。1713年康熙帝又亲自招梅瑴成、何国宗等大批学者,在荣亲王允禄、庄亲王允祉的主持下重新编订历书,《历象考成》的编订工作于康熙六十一年(1722年)结束,共成四十二卷。

《历象考成》与《崇祯历书》的理论系出同源,但具体内容却做了许多修改。知识结构更加的详细、具体,也更易于读者理解。关于视差的基本概念,《历象考成》解释为:

凡求七曜出地之高度必用测量,乃测量所得之数与推步所得之数往往不合。盖推步所得者,七曜距地心之高度,而测量所得者,七曜距地面之高度也。距地心之高度为真高,距地面之高度为视高,人在地面不在地心,故视高必小于真高,以有地半径差也。盖七曜恒星虽皆丽于天,而其高下又各不等,惟恒星天为最高,其距地最远,地半径差甚微,故无视高、真高之差若夫七曜诸天,则皆有地半径差。今欲求太阳之真高,必先得地半径差,欲求地半径差,必先得地半径与日天半径之比例。[6]

《历象考成》从观测、几何原理、影响参数等多方面介绍了地半径差的基本情况,知识层面上虽未出《崇祯历书》范围,但内容更显详尽,图像也更为精美、细致。

相对而言,《历象考成》最大的改变在于《地半径差表》的重编及其造表法的改进。《崇祯历书》的视差造表法需先以太阳模型推出不同位置的日地距离,而《历象考成》由于采用了中国本土学者改进的太阳模型,《崇祯历书》中的数据及方法明显不再适用。况且按一般规律,日地距离本应以视差推得,《崇祯历书》却反其道而行之,似乎也有逻辑颠倒之嫌。基于上述原因,《历象考成》补充了一种通过观测太阳视高度推算日地距离的方法,并以之重新排算《地半径差表》*《崇祯历书》中曾用该方法求解月地距离，亦曾言日地距离也可用此方法求得，但并未给出求解日地距离的具体步骤。《历象考成》编撰时，将之编入求解地半径差的相关章节中，具体步骤考虑到最高、最卑、中距处的不同特点，解说亦有所发挥。。

如图5:甲为地心,乙为畅春园地面,庚为畅春园天顶,子为广州府地面,丑为广州府天顶,戊为太阳,寅为赤道所在。设地半径r=10000000,根据北京、广州的地理纬度,可得两地天顶距之差,即丑庚弧φ=16°49′30″。

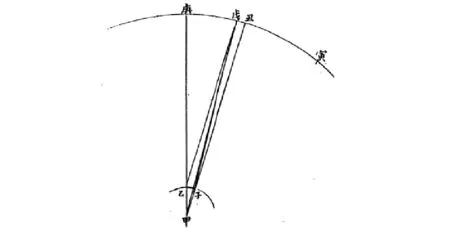
图5　《历象考成》中的地平视差Fig.5　The horizontal parallax in "Li Xiang Kao Cheng"

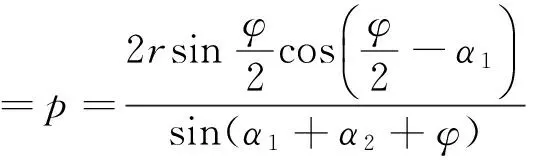
2)测算太阳“中距”处日地距离时,需在春分后八日左右观测畅春园与广州府正午地平高度,所用方法与计算太阳“最高”基本相同,但《历象考成》将时差的影响也考虑在内,较有新意。

测得广州府子午线在京师之西三度三十三分,其午正时乃京师午正初刻十四分也。夫太阳距纬度夏至时每日只差四十余秒,其一刻所差甚微,可不论。若春分时每日差至二十四分,则十四分时可差一十四秒。又春分后太阳自卑而高,纬度既差一十四秒,则午正之高度亦多一十四秒。故必于所测之度减去纬差,始为与京师子午相当地面之高度也[6]。

由于时差的影响,广州府太阳地平高度需减去十四秒,方可得到与京师近乎相同纬度的太阳视地平高度。《历象考成》考虑到时差及太阳地平高度快慢的变化,理论上是较为合理的。依此法,可求得太阳“中距”时日地距离约为1142地半径,与《崇祯历书》相同。

3)《历象考成》测算太阳在本天“最卑”处的日地距离时,没有继续采用观测数据推算,而是采用了模型基本常数间的比例关系:

《历象考成》舍观测而取比例,主要是为了回避冬至时较大的蒙气差。即所谓:“欲以实测求之,奈冬至前后太阳躔本天最卑时,高弧仅二十六度余,蒙气差甚大,难得其真”。[6]“最高”、“中距”、“最卑”三段日地距离推出后,即可利用《崇祯历书》方法计算相应地半径差值。

总体而言,《历象考成》对《崇祯历书》中的地半径差知识进行了较好的查缺补漏。在计算中考虑到诸如时差、蒙气差等因素的影响,使得算法结构更加严密,可见清初历家对西方这套计算模型的掌握已较为熟练。不足的是《历象考成》之法仅在理论上可行,太阳视差本身过于微小,具体操作时同样会遭遇这些细微差距不易观测的事实,数据相较《崇祯历书》仅在秒的数量级有所改变,总体精度提高不大。

3　《历象考成后编》中的太阳视差

《历象考成》的编撰是中国学者对西方天文历法进行独立整理的一次尝试,也做出一些有益调整与改进,但其基本内容还是属于西方古典天文学范畴,与欧洲同时代天文理论相比较为落后,误差之处在行用不久即开始显现。雍正八年(公元1730年),传教士戴进贤(Ignatius Kgler,1680—1746)、徐懋德(A.Pereira,1689—1743)推测《历象考成》预报的月食将会出现“微差”,届时钦天监实地测验,果出现“实测与推算分数不合”的现象,遂奏请将《历象考成》重新修订,获得雍正皇帝批准。[7]乾隆二年(公元1737年),协办吏部尚书顾琮又三次上书,要求对《历象考成》“尽心考研,增补图说”[7],所上条陈准奏后,即开始《历象考成后编》的编撰。乾隆三年(公元1738年),负责修订历书的庄亲王允禄上奏陈述《后编》的主要优点,将太阳视差与蒙气差、椭圆模型并列为三大主要改进,其中太阳视差列于首位,文中言道:

《历象考成》一书,其数惟黄赤大距减少二分,余皆仍《新法算书》西人第谷之书。康熙中西人有噶西尼、法兰德等,发第谷未尽之义,其大端有三:其一谓太阳地半径差,旧定为三分,今测袛有十秒。……戴进贤等皆知其说,因未经验证,不敢遂以为是。[7]

《后编》关于太阳视差最大的改进在于引进了G.D卡西尼(Giovanni Domenico Cassini, 1625—1712)的观测结果。1672年火星冲日期间,卡西尼在巴黎,其助手里奇(Jean Richer,1630—1696)在法属圭亚那岛同时进行观测,测得火星视差25秒,进而推测出太阳最大视差为9.5秒,有史以来第一次得到最为接近真实的数据,推翻了当时太阳系大小的观念,引起了西方学界巨大的兴趣,甚至是狂热。此后,西方天文学家又多次通过观测火星、金星测算太阳视差,修正日地距离。试图将“天文学中最崇高的问题”、“丈量宇宙的标准……天文学里至为重要的基础数值”进一步修正。[8]《后编》编撰时,将其推算方法记录在内,这也是中国首次将具有现代意义的太阳视差引入官方历法。

自后噶西尼等谓日天半径甚远,无地半径差,而测量所系只在秒微,又有蒙气杂乎其内,最为难定。因思日月星之在天,惟恒星无地半径差,若以日与恒星相较,可得其准。而日星不能两见,是测日不如测五星也。土木二星在日上,去地犹远,地半径差愈微。金水二星虽有时在日下,而其行绕日,逼近日光,均为难测。惟火星绕日而亦绕地,能与太阳冲,故夜半时火星正当子午线。于南北两处测之,同与一恒星较,其距恒星若相等,则是无地半径差。若相距不等,即为有地半径差,其不等之数,即两处地半径差之较。且火星冲太阳时,其距地较太阳为近,则太阳地半径差必更小于火星地半径差也。[9]

《后编》求太阳视差之法主要分为两个步骤,其方法如下:

步骤一:求火星地平视差

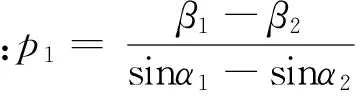
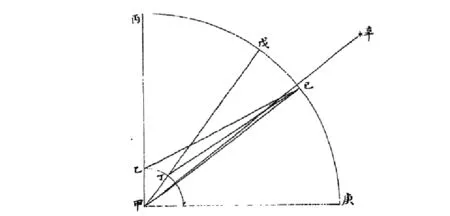
图6　《后编》中的地平视差Fig.6　The horizontal parallax in "Li Xiang Kao Cheng Hou Bian"

《后编》所用算法与《历象考成》并不相同,主要是考虑到太阳视差数值较小,利用了sina≈a(当a较小时)简化计算步骤。书中在此算法之后,又将原始数据按《历象考成》之法重新计算,二者结果基本相合,借此说明《历象考成》误差实源于观测,而非算法之误。

步骤二:推算太阳视差

《后编》较为完整的介绍了卡西尼的太阳视差及其计算原理,对于太阳视差有了进一步的认识,仅从理论方面讲,已与西方相差不远。但可惜的是中国天算家对视差的兴趣主要在于以交食为中心的历法编撰方面,对其宇宙结构方面的意义并不重视。奈何太阳视差十分微小,在历法中基本忽略不计,这也就失去了它在实际计算中的主要价值,致使后续天算家对它的关注度更加低了,至少远没有产生类似于西方的影响。

4　结　语

从明末清初西学初始传入,直到《后编》编撰完成,西方太阳地平视差的核心知识已基本传入中国。在此过程中,中国天算家主流上对这一内容并不排斥,积极将之引入历法之中,相关问题的计算精度也有了一定的提高。

纵观《崇祯历书》到《后编》等几部官方历法中的太阳视差,主要笔墨几乎都集中在几何原理、算法、应用等方面,内容较为全面,基本囊括该知识从古典到近代的主要观点,完全可以满足中国历家编历的需求。可以说在理论知识层面上已与西方相差不远,但对该内容在修正日地距离、探索宇宙真实结构方面的价值,重视程度尚显不足,至少未能引起中国历家的足够兴趣。简单的说,就是更为注重视差的具体数值、推算方法、太阳视位置的精度，而对于视差在其他方面的意义,则仅限于介绍行星内外顺序时的寥寥数语,重视程度不及前者。这一点从庄亲王允禄上奏陈述《后编》主要优点,仅言太阳视差从3′变为10″,而对与此紧密相关的日地距离大幅变化却只字未提,即可见其侧重所在。

官方历书的主要作用是编订历法,重视算法与数据是其必然要求,而民间历算家并无编历任务,似乎也没有多少人对视差在宇宙结构方面的意义感兴趣。虽有不少著作谈及视差,但内容多以历法计算为主,仅有少数论及其他方面,也几乎未出官方历法所限。如熊明遇《格致草》中言:“何为视差?曰:如一人在极西,一人在极东,同一时仰观七政,则其躔度各不同也。七政愈近人者,差愈大;愈远者,差愈小。月最大,日次之,荧惑次之,岁星又次之,填星最小几于无有,故知月最近,填星最远。”[10]几乎照搬《崇祯历书》原文。梅文鼎亦言:“居七政之上,最近大圜最远于地者为恒星。恒星之下,次为土星……。以视差言之,与人目远者视差微,近者视差大,故恒星之视差最微,以次渐增,至月而差极大也。”[11]也仅限于重复《崇祯历书》中视差确定行星顺序的作用。除此之外,梅氏谈及视差的论述基本集中于确定行星视位置方面。即便在《后编》出版之后,中国天算家已经了解了卡西尼视差观测的重大意义,此类状况依然没有多大改观,相对于该问题在西方引起的轰动,差别十分明显。乾嘉时代,一些学者还将视差附会宣夜说,借以论证西学中源。如《宣西通》中言道:“西士视学亦出于宣夜,西法所谓视径、视行、视差,以为非七政之实,人视之则然。此正旁望黄山俯瞰深谷,青非真色墨非有体之说所触类而引申也。”[12]此类论点虽非全不合理,但偏重于附会古籍、盲目自大,距离探索宇宙真实结构的精神更加远了。还有的学者认为天文历法只要保留其“使人主恐惧修省”社会功能就足够了,连是否精确也可放在一边。如《理学逢源》言道:“然古之历疏而切于国计民生之用,后之历密而无当于始。……是谓天变为不足畏,而何以动人主恐惧修省之端。”[13]此类学者虽并不占主流,但也映射出一部分学者对自然知识的看法。

总体而言,《后编》出版之后中国天算家事实上已经了解了太阳视差的相关知识以及卡西尼观测结果带给宇宙模型的巨大变化,但由于国内意识形态的种种原因,虽接受了这些理论和算法,但仅仅是将其视为历法计算中的常数系统,缺少对宇宙真实结构方面的科学诉求,是以未能产生类似西方天文学界的影响。

[1]利玛窦.乾坤体义[M]∥文渊阁四库全书:子部(第787册).台北:台湾商务印书馆,1983:768.

[2]李之藻.浑盖通宪图说[M]∥文渊阁四库全书:子部(第789册).台北:台湾商务印书馆,1983:857.

[3]王英明.历体略[M]∥文渊阁四库全书:子部(第789册).台北:台湾商务印书馆,1983:985.

[4]徐光启编撰,潘鼐汇编.崇祯历书·附西洋新法历书十种[M].上海:上海古籍出版社,2009:43-59.

[5]王萍.西方历算学之输入[M].台北:精华印书馆,1980:45-69.

[6]允禄,何国宗,梅瑴成,等.御制历象考成[M]∥文渊阁四库全书:子部(第790册).台北:台湾商务印书馆,1983:108-119.

[7]赵尔巽.清史稿 [M].北京:中华书局,1991:1670-1671.

[8]庞雪晨.十九世纪金星凌日天象在中西方的反响——从郭嵩焘使英日记切入[J].自然辨证法研究,2014(4):104-110.

[9]梅瑴成,何国宗,戴进贤,等.御制历象考成后编[M]∥文渊阁四库全书:子部(第792册).台北:台湾商务印书馆,1983:11-17.

[10] 熊明遇.格致草[M]∥薄树人.中国科学技术典籍通汇·天文卷.郑州:河南教育出版社,1998:94.

[11] 梅文鼎.历学疑问(卷二)[M]∥梅瑴成.梅氏丛书辑要.鸿文书局石印本,1887.

[12] 许桂林.宣西通(卷二)[M].清嘉庆刻本.

[13] 汪绂.理学逢源(卷七外篇)[M].清道光十八年敬业堂刻本,1838.

(编辑陈镱文)

The spread of the solar parallax in China during later Ming and early Qing Dynasty

ZHANG Qi， SONG Zhi-ye

(The Institute for History of Science and Technology, Inner Mongolia Normal University, Hohhot 010022， China)

During later Ming and early Qing Dynasty, this knowledge was introduced into China, and was introduced into the official calendar system. It was systemized and revised to varying degrees from "Chong Zhen Li Shu" to "Li Xiang Kao Cheng Hou Bian". Consequently the knowledge in China on the theoretical level was nearly comparable to that in the West; however, due to the fact that Chinese astronomy centered on the practical functionality, it remained merely a means of obtaining an important parameter in calendar calculation, absent of the kind of influence enjoyed in the West. Through the comparison of several accounts of solar parallax in the official calendar, this paper studies Chinese astronomers′ and mathematicians′ understanding of the development of this knowledge, and analyzes their degrees of understanding of the solar parallax and science demands.

solar parallax; the astronomical unit; the calendar

2015-11-02

国家自然科学基金资助项目(11373016)；国家自然科学基金资助项目(11261036)；内蒙古高等学校科学研究项目(NJSY16036)；内蒙古师范大学博士科研启动经费项目(2014YJRC027)；内蒙古师范大学科研基金一般项目(2014ZRYB08)

张祺，男，内蒙古呼和浩特人，博士，从事天文学史、科技史研究。

P1-09

A

10.16152/j.cnki.xdxbzr.2016-04-029