集中空调送风静压系统建模与广义预测控制
2016-09-27任庆昌
白 燕,任庆昌
(1.西安建筑科技大学 理学院, 陕西 西安 710055;2.西安建筑科技大学 信息与控制工程学院, 陕西 西安 710055)
集中空调送风静压系统建模与广义预测控制
白燕1,任庆昌2
(1.西安建筑科技大学 理学院, 陕西 西安710055;2.西安建筑科技大学 信息与控制工程学院, 陕西 西安710055)
集中空调空气处理系统因其大时滞、非线性、强扰动、被控对象辨识困难等特点,使得常规PID控制算法的控制效果欠佳。文中在分析集中空调整体系统架构的基础上,基于送风静压控制模型的辨识,提出广义预测控制算法。针对送风静压子模块,采用系统辨识方法,对风机频率风管静压回路进行建模,基于该系统控制模型,设计广义预测控制算法,并用于定静压控制策略的实现。仿真验证和实测结果表明,所设计的算法相对于传统PID控制算法具有较强的跟踪及抗干扰能力。
集中空调;定静压;广义预测控制
空气处理系统作为集中空调系统的重要组成部分,为末端房间输送经过处理的空气,其控制效果直接影响末端系统的运行。其中,送风管道静压系统的控制是根据系统末端负荷的变化,调整送风机频率、改变送风管道静压,进而满足空调在部分负荷下的水-空气的热交换。目前,工程中常用的控制算法是PID算法,但系统具有非线性、大滞后、时变性、强扰动、不确定性等缺点,该情况下难以对其建立精确的数学模型。同时,系统的控制环节常处于不断调节状态,这使得常规PID控制难以达到预期的控制效果。
Clarke和Mohtadi等学者提出的广义预测控制算法(Generalized predictive control,GPC),在参数模型的基础上,采用在线递推式算法估计模型参数,取代原模型参数。该算法基于反馈校正的思想,在控制过程中进行滚动优化和多步预测,以便充分利用被控对象的动态行为信息,从而使系统的控制性能得到提高,适应被控对象的时滞特性和阶次变化[1]。
孙灵芳等将GPC算法应用于球磨机制粉系统的建模[2],Dimogianopoulos等学者将GPC算法应用于飞行器自动阀门的控制[3],Beschi等学者设计了线性GPC控制算法并用于太阳炉的控制[4],Ouari等学者对风能转换系统进行了非线性广义预测控制的实时仿真[5]。上述研究成果说明GPC算法在工业、航空、能源等领域均取得了较好的控制效果,具有较高的应用价值。此外,在集中空调控制领域中,GPC算法的研究与应用也得到了认可与关注。白建波等学者将GPC算法应用于表冷器出风温度的控制[6],文献[7]和[8]研究了HVAC系统基于分散辨识方法的GPC控制以及基于递阶结构的GPC-PID控制策略,杨洪祥等将GPC算法用于变风量空调末端系统的仿真与控制[9],West等学者对商业建筑中暖通系统的模型预测控制与优化进行了验证[10]。上述研究成果表明,广义预测控制算法在暖通空调领域中的应用取得了较好的控制效果,较常规PID控制算法具有明显优势。
本文设计了广义预测控制算法,在仿真实验的基础上,将其部署于西安建筑科技大学的智能建筑变风量集中空调系统实验平台,完成送风系统的定静压控制。
1 集中空调系统整体架构
本文所依托的变风量集中空调系统平台包括水侧子系统、风侧子系统以及末端子系统3大模块。水系统的主要设备有2台冷机、3台冷却水泵、3台定频一级泵、1台变频二级泵;风系统的主要设备有2组空气处理机(AHU),其中各包含一个变频风机;末端系统包含6组变风量末端机箱(VAVBOX);此外还包括各系统的传感器、控制器和执行器,该系统的整体结构如图1所示。本文针对风系统中的静压控制回路进行相关研究。
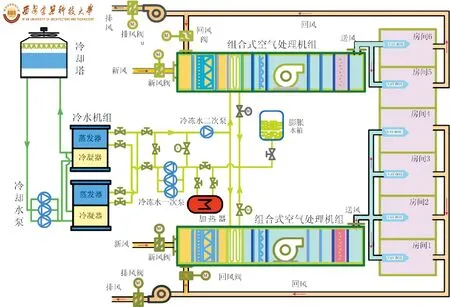
图1 西建大集中空调系统实验平台结构示意图Fig.1 Central air conditioning system diagram in XAUAT
2 送风静压控制模型的辨识
由于空调送风静压系统涉及变量较多,难以得出精确的机理模型,本论文采用系统辨识方法建立该系统的控制模型。该方法将系统视为一个黑箱,通过对系统的输入输出数据进行测量,根据动态系统的多组输入输出测量数据,基于某种准则,通过统计分析得到它的数学模型,所得模型是对实际系统一个合适的近似,适用于内部机理无法直接获得的系统建模[11-12]。
本实验系统中,空气处理系统的送风机为变频控制,其频率变化范围为20~50Hz,送风管静压控制系统的辨识步骤如下:
Step1绘制并分析风管静压随风机频率变化的特性曲线,由此确定静压变化范围的线性区间。根据现场经验,在线性区间内选取风机频率的变化范围为20~45Hz,频率增加步长为1Hz,采样周期为5s,采集该过程中风机频率及对应的风管静压值。改变末端风阀开度,并进行多次实验,从中随机选取两组实验数据,绘制“风机频率-静压”特性曲线,如图2所示。静压随风机频率变化的线性区间约为20~45Hz。
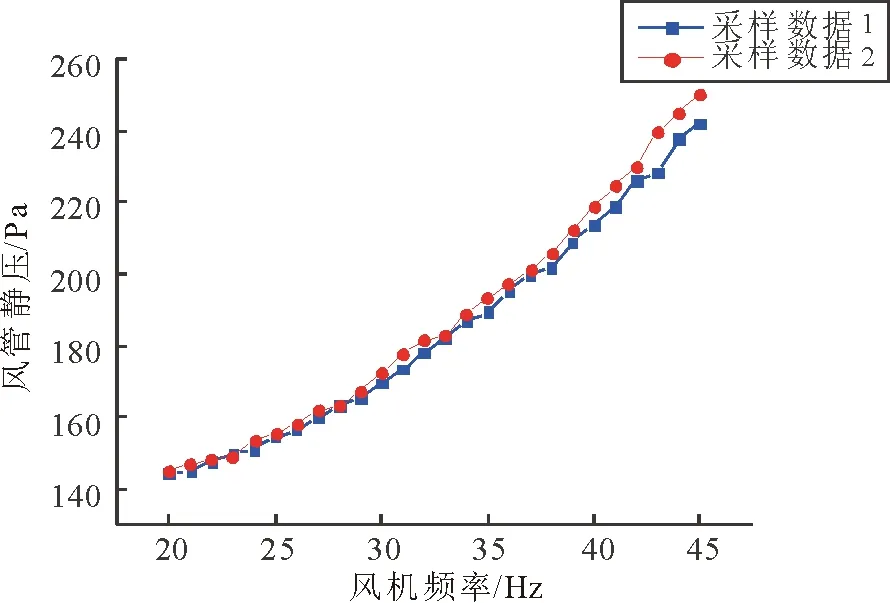
图2 AHU1风机频率-静压特性曲线Fig.2 Curve of fan frequency-static pressure
Step2完成“风机频率-静压”阶跃响应测试。在线性区间内,选择风机频率在20~35Hz之间进行阶跃(即风机转速在1 200~2 100r/min之间阶跃),进行多次实验,随机采集4组数据进行分析。图3为测试结果,根据图3可知,阶跃实验中控制单元平均延迟时间为4.5s,系统的过渡过程时间Ts为14.5s。
Step3将正弦信号加载至风机频率控制端,经试验求得系统的截止频率。根据Step1选取的线性区间,选择正弦波信号在20~35Hz范围内变化、幅值为7.5的信号,分别采集相应的风机频率及风管静压数据。图4为静压随频率变化的趋势,根据文献[12]的方法求得该系统的截止频率fmax为0.04Hz。
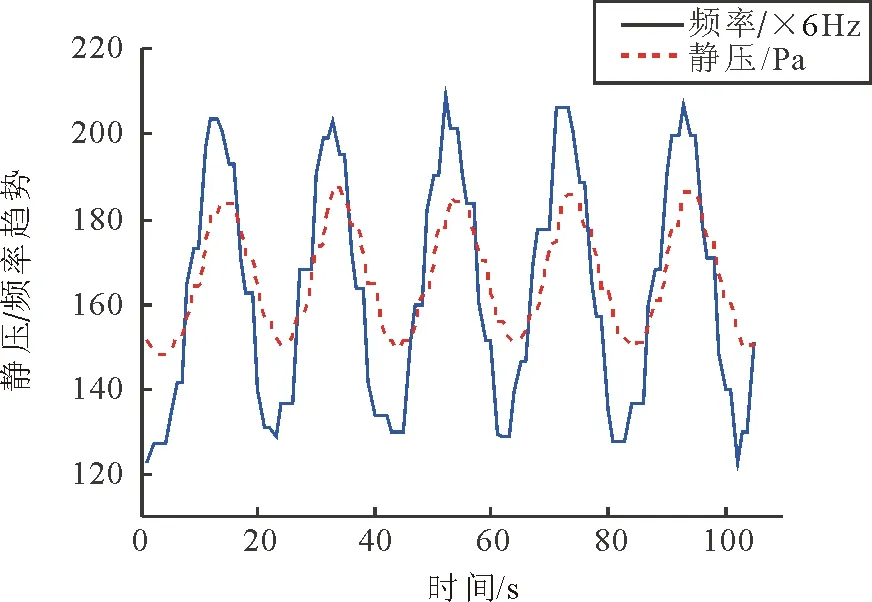
图4 静压随频率的变化趋势Fig.4 Variation trend of static pressure on frequency
经过辨识,该工况下得到的静压控制系统的动态模型过程传函表示为一阶时滞模型,
(1)
3 广义预测控制(GPC)算法的仿真
3.1GPC算法原理
随着自适应控制理论的成熟与完善,广义预测控制逐步发展,并以其预测模型、滚动优化及在线校正等优势迅速应用于工业过程控制。
广义预测控制算法以受控自回归积分滑动平均模型为基础,建立被控对象的数学模型[1,13],
A(z-1)y(t)=
B(z-1)u(t-1)+C(z-1)ξ(t)/Δ。
(2)
其中,A(z-1),B(z-1),C(z-1)为后移算子z-1的多项式,分别为
A(z-1)=1+a1z-1+…+anaz-na=
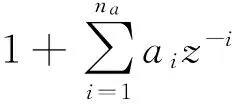
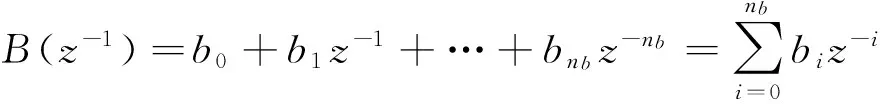
C(z-1)=1+c1z-1+…+cncz-nc=
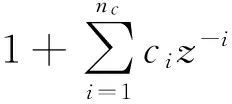
Δ=1-z-1。
式中,u(t-1),y(t),ξ(t)分别为系统的输入量、输出量和均值为0的白噪声序列,Δ为差分算子。通常令C(z-1)=1,以简化问题。
根据预测理论,可利用t时刻之前的输入输出数据,借助丢番图(Diophantus)方程进行计算,得出j步后输出值y(t+j)的最优预测值。
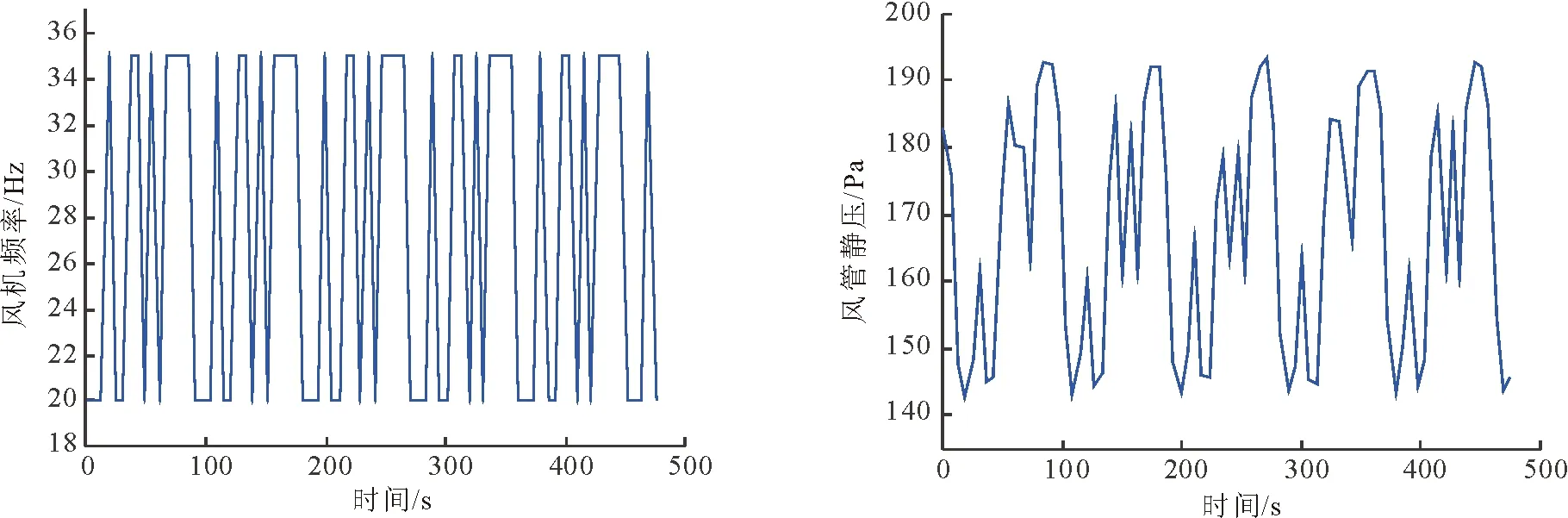
图5 AHU1风机频率-静压控制系统输入与输出数据Fig.5 Input and output of frequency-static pressure system of AHU1
Diophantine方程为
(3)
式中Ej,Fj,Gj,Hj为j-1阶的多项式矩阵。因此,j步最优预测控制为y(t+j)=GjΔu(t+j-1)+Fjy(t)+HjΔu(t-1)。
广义预测控制算法常用的性能指标函数为
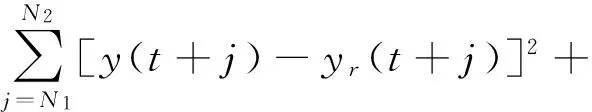
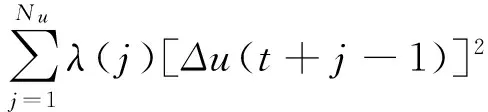
(4)
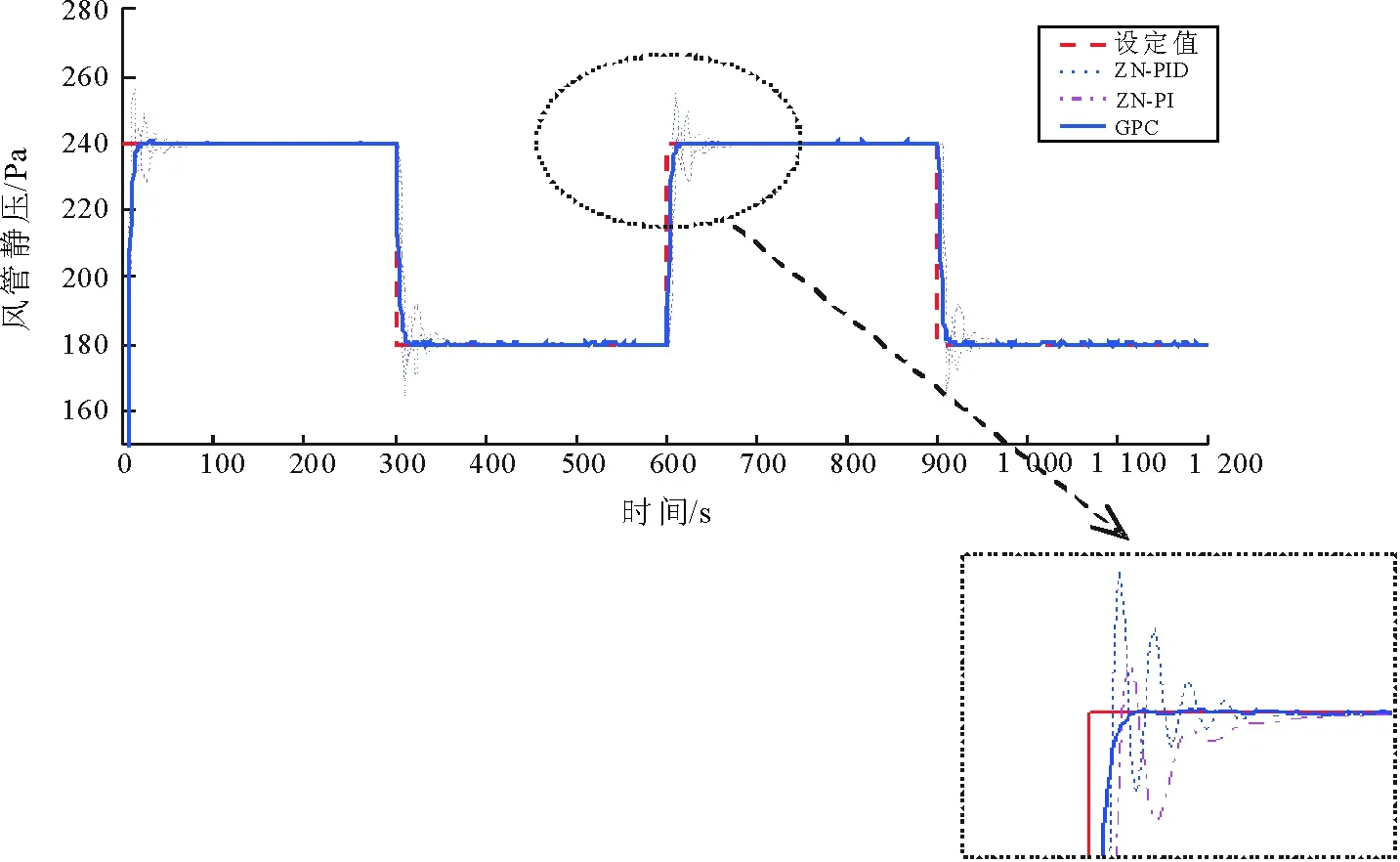
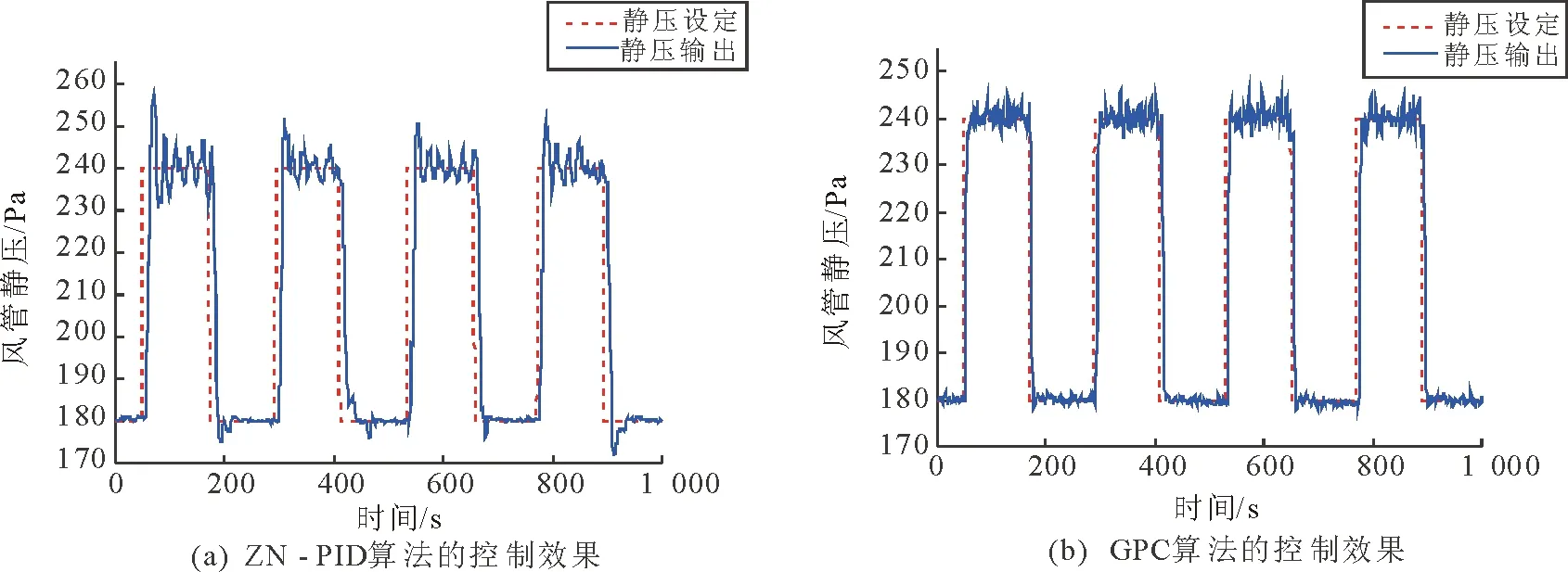
式中,E表示数学期望,yr表示控制对象输出的参考值,N1,N2和Nu分别表示优化时域的起始值、终止值和控制时域。一般取Nu u(k+j-1)=u(k+Nu-1),j>Nu。 (5) λ(j)为控制加权系数,通常假定其为常数λ。控制目标是使被控对象的输出能够跟踪参考轨迹, yr(t+j)=αyr(t+j-1)+(1-α)y(t), j=1,2,…,N。 (6) 其中,yr为恒定值,y(t)为当前时刻实际输出值,yr(t+j)为参考轨迹,α为柔化系数(0<α<1)。通过求解,可得使J最小的控制增量的向量为 U=(GTG+λI)-1GT[yr(t)- Fy(t)-HΔu(t-1)]。 (7) 3.2控制算法的仿真研究 中央空调风管静压控制回路以送风管道静压为被控对象,本文主要研究空气处理机组1的风管静压控制。采用的广义预测控制算法,其原理图如图6所示,其中w(k)为静压设定值,u(k)为控制输入值,y(k)表示当前时刻静压的实际输出量,ym(k+i)表示预测模型的计算值,ye(k+i)为校正输出,yr(k+i)为控制参考轨迹,d(k)是随机扰动。 图6 GPC控制原理Fig.6 Principle diagram of generalized predictive control 针对本系统的风机频率-静压模型,分别采用ZN-PID(基于Z-N整定法的PID控制)算法、ZN-PI算法及GPC算法对静压控制过程的动态变化进行仿真,结果如图7所示,风管静压设定值在240~180Pa之间进行阶跃。从图7中可看出,GPC算法较ZN-PID算法有明显优势。 图7 送风静压控制过程的仿真图Fig.7 Simulation of static pressure control process 在仿真实验的基础上,分别将两种算法部署于实验平台上,进行仿真实验,对风管静压控制回路进行定静压控制,并对比和分析控制效果。静压设定值选取180~240Pa之间进行阶跃实验,基于两种不同控制算法的风管静压控制实测数据如图8所示。 图中所示的实验结表明,对于阶跃响应控制过程,两种算法的跟随性较好。从图8可知,系统控制的超调量、上升沿及下降沿的调节时间等情况如表1所示。进一步考察定静压控制策略下ZN-PID控制算法对于扰动的适应能力,实验中分别模拟末端4个房间不同负荷的情况,初始时刻,各末端房间的风阀开度分别为42.46%,37.68%,60%及40.12%。该区域AHU的送风静压设定值为200Pa,运行过程中不断调节3号房间的末端风阀(VAV3)开度,以此模拟3号房间的负荷变化情况,实验过程中保持其余末端风阀开度恒定。图9所示为静压和风机频率控制情况,图10为VAV3阀门开度变化情况。 图8 风管静压阶跃控制Fig.8 Step response of static pressure 超调量/%上升沿的调节时间/s下降沿的调节时间/sZN-PID7.373217GPC1.131612 图9 基于PID算法的AHU1送风静压控制Fig.9 Static pressure control based on PID algorithm 图10 VAV3风阀开度变化情况Fig.10 Air valve changes of VAV3 根据图9所示,末端风阀开度的每次变动都会引起送风管道的静压波动,但在该控制策略下,扰动能够很快被克服,并恢复设定值。 为观察GPC算法对扰动的适应能力,采取类似的实验方案,并将送风静压设定为220Pa,运行时不断调节VAV3的风阀开度,且保持其余末端风阀开度恒定,静压及风机频率变化情况如图11所示,VAV3风阀开度变化情况如图12所示。 由图9和图11可见, 两种算法对于扰动的抑制情况有所差异。 系统末端负荷变化导致VAV风阀开度的调整, 进而引起送风管道静压的波动, 对于此类扰动情况, PID算法控制过程中震荡较明显, 但GPC算法除在调节初期出现超调外, 整个控制过程能够较快地恢复设定值, 且控制平稳。 图11 基于GPC算法的AHU1送风静压控制Fig. 11 Static pressure control based on GPC algorithm 图12 VAV3风阀开度变化情况Fig.12 Air valve changes of VAV3 本文在对集中空调整体系统架构进行分析的基础上,采用系统辨识方法,建立送风静压控制模型,采用GPC算法的设计方案,并用于送风系统的定静压控制。实验结果表明,对于阶跃控制过程,两种算法的跟随性较好,而GPC算法的超调量、上升沿及下降沿的调节时间均优于PID算法;对于扰动实验过程,对于由末端负荷变化引起的风管静压波动,GPC算法除在调节初期出现超调外,整个过程控制平稳,优于PID算法。综上,所采用的GPC算法设计方案具有较强的跟踪性能和抗干扰性能,控制效果优于传统PID算法,适用于集中空调风系统的控制。 [1]CLARKE D W, MOHTADI C, TUFFS P S. Generalized predictive control [J]. Automatica, 1987, 23(5): 149-160. [2]孙灵芳,孙晶淼. 球磨机制粉系统建模及广义预测控制的研究与应用 [J]. 系统仿真学报,2015,27(6):1329-1337. [3]DIMOGIANOPOULOS D, PETRATOS V, KOPSAFTOPOULOS F, et al. A GPC-based auto-throttle with robust fuel-efficient operation in 4D flights [J]. Aerospace Science and Technology, 2015, 40: 128-137. [4]BESCHI M, BERENGUEL M, VISIOLI A, et al. Implementation of feedback linearization GPC control for a solar furnace [J]. Journal of Process Control, 2013, 23(10): 1545-1554. [5]OUARI K, REKIOUA T, OUHROUCHE M. Real time simulation of nonlinear generalized predictive control for wind energy conversion system with nonlinear observer [J]. ISA Transactions, 2014, 53(1): 76-84. [6]白建波,王孟,苗国厂,等. 基于广义预测控制算法的表冷器出风温度控制 [J]. 制冷与空调,2015,29(1):78-82. [7]XU M, LI S Y. Practical generalized predictive control with decentralized identification approach to HVAC systems [J]. Energy Conversion and Management, 2007, 48(1): 292-299. [8]XU M, LI S Y, CAI W J, et al. Effects of a GPC-PID control strategy with hierarchical structure for a cooling coil unit [J]. Energy Conversion and Management, 2006, 47(1): 132-145. [9]杨洪祥. 变风量空调末端广义预测自校正控制 [J]. 控制工程,2009,16(增):57-60. [10] WEST S R, WARD J K, WALL J. Trial results from a model predictive control and optimisation systemfor commercial building HVAC [J]. Energy and Buildings, 2014, 72: 271-279. [11] 侯媛彬,汪梅,王立琦. 系统辨识及其MATLAB仿真[M]. 北京:科学出版社,2004. [12] 王秀峰,卢桂章. 系统建模与辨识[M]. 北京:电子工业出版社,2004. [13] 席裕庚. 预测控制[M]. 北京:国防工业出版社,1993. (编辑李静) Static pressure system modeling and generalized predictive control for central air conditioning system BAI Yan1, REN Qing-chang2 (1.School of Science, Xi′an University of Architecture and Technology, Xi′an 710055, China; 2.School of Information and Control Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China) The conventional PID control algorithm is ineffective due to the characteristics of large time delay, nonlinearity, strong disturbance, and identification difficulties of air-handling system. In this paper, the generalized predictive control algorithm was proposed based on the identification of static pressure control model after analyzing of the overall architecture of the central air-conditioning system. The control model for the loop of fan frequency and static pressure was constructed by using system identification method and the generalized predictive control algorithm was designed and applied to static pressure control strategy. The simulation and experimental results show that the algorithm has strong tracking and anti-disturbance ability over the traditional PID algorithm. central air conditioning system; constant static pressure; generalized predictive control 2015-12-22 国家自然科学基金资助项目(51508446);陕西省教育厅自然科学专项基金资助项目(14JK1396);西安建筑科技大学基础研究基金资助项目(JC1516);西安建筑科技大学人才科技基金资助项目(RC1515) 白燕,女,陕西西安人,副教授,博士生,从事智能建筑环境技术、智能控制技术研究。 TP29 A 10.16152/j.cnki.xdxbzr.2016-04-009
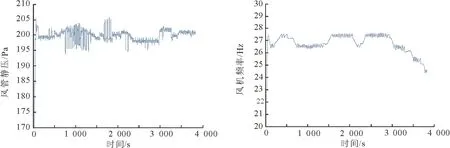
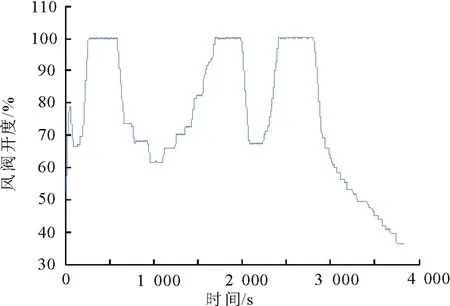
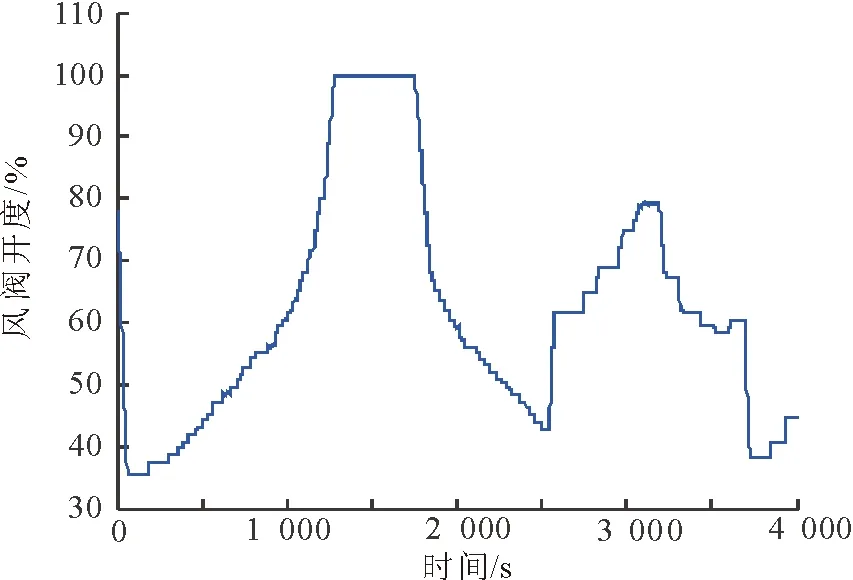
4 实验结果及分析


5 结 语
