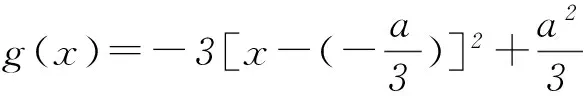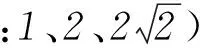探究“双变量”不等式与函数“单调性”的联系
2016-09-26湖北
高中数理化 2016年5期
◇ 湖北 刘 丽
(作者单位:湖北随州一中)
探究“双变量”不等式与函数“单调性”的联系
◇湖北刘丽
以函数为载体,设置的“双变量”不等式恒成立问题,往往与函数的“单调性”具有某种紧密的联系.那么如何寻找这种联系,并加以灵活运用呢?请看以下归类解析.
1 “双变量”分式不等式


又由h′(x)=-3x2+12=-3(x+2)(x-2)可知, 函数h(x)的单调递增区间为(-2,2). 所以
(2m,m+1)⊆(-2,2),



2 “双变量”绝对值不等式



f(x2)-h(x2) (答案:[3/2,+∞)) 综上可知,求证结论成立. 变式3已知函数f(x)=(a+1)lnx+ax2+1,求证:当a≤-2时,对任意x1、x2∈(0,+∞),不等式|f(x1)-f(x2)|≥4|x1-x2|恒成立.(证明略) 综上,处理此类问题的关键是:先对“双变量”不等式适当变形,以便从不等式的结构特点出发,观察、确定相关函数的“单调性”;然后再借助导数知识和函数性质加以灵活处理. (作者单位:湖北随州一中)

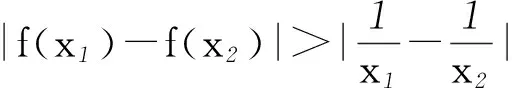
3 含参“双变量”不等式的证明


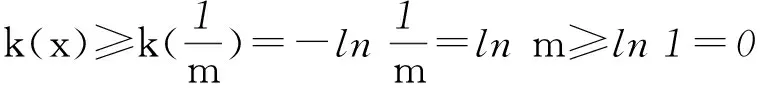

4 隐含的“双变量”不等式