探究一道轮换不等式自主招生题及变式题的多种证法

◇　浙江　甘大旺(特级教师)

(作者单位：浙江省宁波市北仑明港中学)



探究一道轮换不等式自主招生题及变式题的多种证法

◇浙江甘大旺(特级教师)

轮换不等式中任意2个字母对换后稍作整理仍与原不等式同形,2014年哈尔滨工程大学自主招生数学试卷的最末一题就是轮换不等式证明题.

本文以此题及变式题为例,介绍证明轮换不等式的4种常用方法．

证法1由于a+b+c=1且a、b、c∈R+,则3次运用均值不等式得

证法2由于a+b+c=1且a、b、c∈R+,则运用柯西不等式得到

所以,原不等式正确．

变式已知3个正数a、b、c的和等于1.证明:

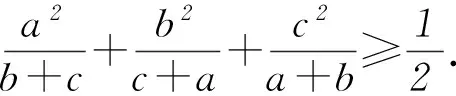
1) 若f(x)在区间D内是上凹函数(即二阶导数f″(x)>0),则对任意的n个实数x1、x2、…、xn∈D,其中正整数n≥2,则恒有不等式

(其中“≥”当且仅当x1=x2=…=xn时取“=”);

2) 若f(x)在D内是下凹函数,则就把1)中不等式的“≥”替换成“≤”即可．

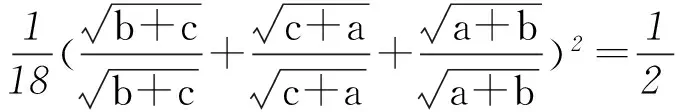
所以,原不等式正确．

链接练习

1. 若n(≥2)个正数a1、a2、…、an的和等于定值A,求证:

2. 已知△ABC为锐角三角形,证明

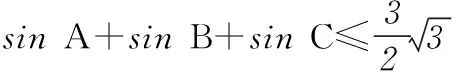
3. 已知n(≥2)个正实数a1、a2、…、an满足a1+a2+…+an=1,求证:

链接练习解法提示

1. 用4种方法都可证明．

2. 宜用琴生不等式．

3. 用均值不等式或柯西不等式．

4. 综合用切比雪夫不等式和均值不等式．

(作者单位：浙江省宁波市北仑明港中学)