例析滴定原理在高考解题中的拓展运用——以江苏高考试题为例

◇　江苏　李宗来

(作者单位：江苏省响水中学)



例析滴定原理在高考解题中的拓展运用

——以江苏高考试题为例

◇江苏李宗来

近几年来,由酸碱中和滴定实验的基本原理延伸而来的氧化还原滴定、配位滴定、沉淀滴定等实验在高考中经常出现,考查方式涉及滴定实验基本操作、滴定终点的判断、误差分析、化学计算等．本文特以近年来江苏省高考试题为例分析滴定原理在高考解题中的拓展运用,以期提高解题准确率．

1　运用氧化还原滴定计算某物质的纯度

没有提供反应方程式的氧化还原滴定,通过得失电子守恒建立氧化剂与还原剂之间数量关系,再由消耗的还原剂(氧化剂)的量来确定某氧化剂(还原剂)的量,同时结合元素守恒、电荷守恒进行相关的计算．

n(Mn3+)×1=n(Fe2+)×1=

20.00×10-3L×0.050mol·L-1=1.00×10-3mol.

根据Mn元素守恒,m(MnSO4·H2O)=1.00×10-3mol×169g·mol-1=0.169g.所以纯度是

2　运用氧化还原滴定计算某离子的浓度

滴定实验操作试题能甄别出学生是否动手做过实验,因此重要的化学实验要亲自动手去做,要由对实验的感性认识上升到理性的思考,提高操作能力、思考能力、文字表达能力;对于已经给定反应方程式的氧化还原滴定,要先列出已知量与未知量的关系式,然后计算求解．

(1) 称取一定量已除去油污的废铁屑，加入稍过量的稀硫酸，加热、搅拌，反应一段时间后过滤.反应加热的目的是________.

(2) 向滤液中加入一定量H2O2氧化Fe2+．为确定加入H2O2的量,需先用K2Cr2O7标准溶液滴定滤液中的Fe2+,离子方程式如下:

① 向滴定管中注入K2Cr2O7标准溶液前,滴定管需要检漏、________和________．

② 滴定xmL滤液中的Fe2+,消耗amol·L-1K2Cr2O7标准溶液bmL,则滤液中c(Fe2+)=________mol·L-1．

3　运用氧化还原滴定计算某物质的组成

运用氧化还原滴定来计算物质的组成或化学式,滴定只是计算组成中某微粒量的一步,要结合其他计算,运用元素守恒、电荷守恒、质量守恒关系,要特别注意题干中量之间的关系．

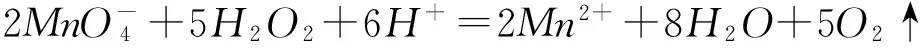
通过计算确定样品的组成(写出计算过程)．

由离子反应列关系可得:

n(H2O2)=5/2×0.020mol·L-1×

25.00mL/1000mL·L-1=1.25×10-3mol,

m(Na2SO4)=142g·mol-1×

2.50×10-3mol=0.355g,

m(H2O2)=34g·mol-1×

1.25×10-3mol=0.0425g.

根据质量守恒关系可得

n(H2O)=(1.770g×25.00mL/100. 00mL-

0.355g-0.0425g)/18g·mol-1=

2.50×10-3mol.

x∶y∶z=n(Na2SO4)∶n(H2O2)∶n(H2O)=2∶1∶2.

Na2SO4-H2O2加合物的化学式为2Na2SO4·H2O2·2H2O.

4　运用配位滴定计算某物质的化学式

配位滴定是以中心离子(金属离子)与配体形成配合物的反应为基础的一种滴定分析法,以EDTA(Na2H2Y)做标准液,可用于对物质组成中某金属离子含量的测定,计算时根据提供的反应,列出EDTA与金属离子的关系式,求出金属离子含量,再结合其他计算求出化学式．

(1) 若滴定管在使用前未用EDTA标准溶液润洗,测得的Ni2+含量将____(填“偏高”“偏低”或“不变”)．

(2) 通过计算确定硫酸镍铵的化学式_________(写出计算过程)．

n(Ni2+)=n(EDTA)=0.040mol·L-1×

31.25mL×10-3L·mL-1,

若在使用前未用EDTA标准溶液润洗,会使EDTA的实际浓度偏小,消耗的体积变大,计算的值变大．

(2) 根据元素守恒关系可得:

根据电荷守恒关系可得:

2.500×10-3mol.

m(Ni2+)=59g·mol-1×1.250×

10-3mol=0.07375g,

10-3mol=0.045g,

2.500×10-3mol=0.240g.

根据质量守恒关系可得

0.045g-0.24g)/18g·mol-1=1.250×10-2mol.

硫酸镍铵的化学式为(NH4)2Ni(SO4)2·10H2O.

5　运用沉淀滴定计算某物质的质量分数

沉淀滴定是以沉淀反应为基础的一种滴定分析方法．用AgNO3标准溶液滴定Cl-,加入铬酸钾作指示剂,是测定Cl-含量的重要手段,AgCl先沉淀,当砖红色的铬酸银沉淀生成时,表明Cl-已沉淀完全,指示终点已经到达.此法方便、准确,应用很广．

(1) 上述测定过程中需用溶液润洗的仪器有____．

(2) 计算上述样品中CaCl2·2H2O的质量分数为________．

(3) 若用上述方法测定的样品中CaCl2·2H2O的质量分数偏高(测定过程中产生的误差可忽略),其可能原因有____________．

(2) 设CaCl2·2H2O质量分数为w,根据关系式:

CaCl2·2H2O～2Cl-～2AgNO3

1472

w×0.750 0×25/250

0.050 00×0.020 39

解得:w=99.9%.

(3) 根据(2)中的关系式可得:若Cl-偏多,则滴定的结果就会偏高,所以样品中若混有含氯量高于CaCl2的NaCl或CaCl2·2H2O晶体中的结晶水失去一部分,都能使CaCl2·2H2O的质量分数偏高．

(作者单位：江苏省响水中学)