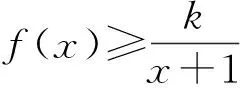基于学生困惑的导数教学策略分析*

●庄迁福

(温州第二高级中学　浙江温州　325000)



基于学生困惑的导数教学策略分析*

●庄迁福

(温州第二高级中学浙江温州325000)

数学教育应遵循教育规律，依据数学内在的性质特点，顺从具体的学情而行．根据这一指引，教学中应先调整学生学习的困惑点，再进行教学策略分析，使数学课堂变成绿色的思维场．文章从学生导数学习中4个常见的困惑点进行分析，制定相应的教学策略.

学生困惑;教学策略;比较判断法

绿色的数学教育倡导2个方向：一是自然，一是绿色.“自然”即循道而行，数学教育应遵循教育规律，依据数学内在的性质特点，顺从具体的学情而行,这为我们应该怎么教提供了方法与立足点；“绿色”意为生机与活力，数学教育应该充满生机与活力，这为教学设计提出了出发点与要求．因此，数学课堂上不仅应有鲜花，还应该有“花开的声音”，也只有自然、绿色的数学教育才更有效[1]．笔者根据这一指引，在教学中先调整学生学习的困惑点，再进行教学策略分析，使数学课堂变成绿色的思维场．

困惑1分类讨论这么多，怎么进行？

导数章节中考查的函数通常含有参数，因此对函数的单调性判断需要分类讨论.而学生面对多种分类讨论时，时常找不到讨论的分界点，也有学生表示能看懂答案听明白，自己却无从下手.笔者认为，解决学生这一困惑，教师应在教学中引导学生关注导函数的正负，设计讨论函数单调性的题组，再归纳设计一个算法，回归数学本质，授人以渔.

例1“导数在研究函数中的应用”第2课时一个教学片断.

1)已知函数f(x)=(x2+ax-2a2+3a)ex(其中x∈R，a∈R)，求函数f(x)的单调区间；

3　结论

通过第1课时的学习，学生已经学会通过导数来判断简单函数的单调性，但对含参函数的单调性还没有掌握.笔者选择了3道高考题的第1)小题编制了上述题组.第1)题中的导函数可以因式分解为

f′(x)=ex(x+2a)(x+2-a)，

通过比较2个根的大小来解决；第2)题中的导数可化简为

增加了函数的定义域作为区间要求；第3)题中的导数为

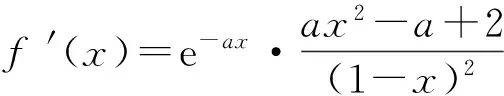
既要分析导函数的零点是否存在，又要考虑定义域{x|x≠1}这个隐藏条件.

学生完成这3道题后，笔者与学生一起归纳，既有先求函数定义域的要求，也有求导过程的一些总结，更重要的是一起设计一种解决此类问题的方法，可分3步完成，即操作时问自己3个问题:导函数有没有根？根在不在区间上？如何比较根的大小？优先考虑没有根，根不在区间上.有了这一指引，学生轻松处理了单调性问题，后面的教学中又通过对关键词的归纳、对导数解答题与客观题的总结，使得解决此类问题有迹可循.

困惑2构造函数还是参变分离，怎么选择？

在导数解题时，学生一拿到题目常常直接构造函数，然后对函数进行求导，若是复杂函数还要多次求导，有成功但失败更多.紧接着，教师也会将参变分离这一方法与构造函数的方法进行对比，对部分题目避免复杂的讨论.有了这2种方法，学生的困惑又产生了，该怎么选择呢？除了本题的2种解题方法外，笔者认为学生更需要一种分析题目的习惯与能力.在教学中，教师应给足时间让学生去尝试，并表述自己的体会与收获，让学生采用各走一步再对比的方法来选择，不划定具体标准选择路径，同时教师需对方法进行延伸.

例2设函数f(x)=ex-e-x，若对任意x≥0,都有f(x)≥ax,求实数a的取值范围.

(浙江省高中数学作业本第30页第14题)

笔者统计了学生的完成情况，主要有以下3种：

情况1构造函数g(x)=ex-e-x-ax，求导得

g′(x)=ex+e-x-a，

接着因求不出导数的零点而放弃了.

情况2进行参变分离，原不等式可转化为

情况3情况1或情况2遇到障碍，去尝试另一种方法.

笔者在分析时，先让出现情况3的学生谈谈自己的想法：为什么先想到这一方法，再对比2种方法在运用时的优缺点.学生的第一反应就是当下的学情，到底哪一种方法更优，建议“先各走出一步，再对比”，对于一般比较简单的问题可考虑参变分离.

①当a≤2时(对应导数没有根)，g(x)在[0,+∞)上单调递增，g(x)≥g(0)=0恒成立，符合条件；

②当a>2时(对应导数有根)，由于g′(x)在[0,+∞)上单调递增，且g′(0)·g′(lna)<0，故存在x0∈(0,lna)使得g′(x0)=0，从而当x∈(0,x0)时有g(x)

困惑3这样做可以吗？

例3已知函数f(x)=(a+1)lnx+ax2+1．

1)讨论函数y=f(x)的单调性；

2)设a≤-2，求证：对任意x1,x2∈(0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|．

完成证明后，笔者又给出拉格朗日中值定理进行对比，学生的疑惑得到解决.类比证明过程中构造函数的思想，对比结构，也就容易想到原不等式可转化为：当x1≥x2时，

f(x2)+4x2≥f(x1)+4x1，

再证明g(x)=f(x)+4x在区间(0,+∞)上单调递减即可.

困惑4这么巧妙，怎么想得到？

近几年高考中出现的导数解答题，其最后一问常常结合了数列与不等式，需要构造不等式然后利用放缩技巧来解决，学生感叹：太巧妙了，怎么想得到？笔者认为：在教学中，教师不宜过分渲染技巧，这样容易让学生望之则怯，应注重通法通解，对复杂问题拆分，可采用比较判断法来进退自如[3]，赋予学生发现数学形式美的眼睛.

2)求证：[(n+1)!]2>(n+1)·en-2(其中n∈N*)．

证明第2)小题有2种方法：一是从形式上看，可用数学归纳法证明；二是从背景上看，可构造导数不等式.学生反映花了很多时间去看解析才看懂，觉得都是技巧，自己无法想到.

针对这一情况，笔者先将第2种方法进行拆解，分4步完成：寻找导数题干中的不等式；对参数进行赋值，通常是解集的边界值；写出对x赋值为n的表达式；部分放缩求和.

原不等式2边取对数后变为

2[ln1+ln2+…+ln(n+1)]>ln(n+1)+n-2，

具体选择可以从不等式其他部分的相似度考虑.运用到本题中：

左边：an=2ln(n+1)，

右边：bn=ln(n+1)+n-ln(n)-(n-1)-

只需证明an>bn，即

还学生一片绿色自然的数学课堂，就要扎根于学生的经验，根据学生的各种困惑制定教学策略，分析有效的数学思维能力的发展．这样的课堂，伴随着学生的自我改造、重组和更新，使课堂呈现一片生机勃勃．

[1]陈勤，王贵文．让学生在课堂上生长——从一节高考复习课谈起[J]．中学数学教学参考，2014(5)：30-32.

[2]董裕华．高等数学背景下的高考数学命题探析[J]．中学数学，2007(4)：60-64.

[3]徐章韬．比较判断法解析高考试题[J]．数学教学，2009(2)：43-45.

*收文日期：2016-04-25；2016-06-01

庄迁福(1986-)，男，浙江温州人，中学一级教师.研究方向：数学教育.

O122

A

1003-6407(2016)09-04-03