2016年山东卷理科第21题的深度探究*
2016-09-23韩长峰
●韩长峰
(太和中学 安徽阜阳 236600)
●卫小国
(单县一中 山东菏泽 274300)
2016年山东卷理科第21题的深度探究*
●韩长峰
(太和中学安徽阜阳236600)
●卫小国
(单县一中山东菏泽274300)
探究2016年山东省数学高考理科第21题,挖掘隐含背景,领悟命题思想,明确考查方向,为高三圆锥曲线的复习教学和压轴突破提供研究方法与解题技巧.
试题推广;纵向研究;横向拓展
2016年山东省数学高考理科第21题的第2)小题考查直线与抛物线、椭圆的位置关系等基础知识及转化化归的基本数学思想;以证明点在定直线上为载体,考查推理论证能力和运算求解能力,检测创新解题意识[1].笔者对此题进行了分析与研究,现撰文以展示探究历程.
1 试题再现
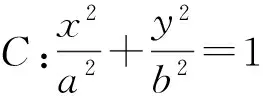
1)求椭圆C的方程.

图1
2)设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的2个点A,B,线段AB的中点为D,直线OD与过点P且垂直于x轴的直线交于点M.
①求证:点M在定直线上;
②略.
分析易求得椭圆C的方程为x2+4y2=1,下面对第2)小题的第①问进行探究.


设A(xA,yA),B(xB,yB),D(xD,yD),联立方程组
得
(4m2+1)x2-4m3x+m4-1=0.


于是直线OD的方程为

联立方程组


作差得

即
(xA+xB)(xA-xB)+4(yA+yB)(yA-yB)=0,
从而
kODkAB=-4.


解完题,笔者仍觉意犹未尽.因命题专家精心编制的试题往往将问题的抽象本质隐藏,而仅呈现出具体的表象[2].试题揭示了什么规律,其命制的源头何在?笔者进一步从一般性推广、纵向探究和横向拓展进行思考,终获玄机.
2 一般探究及推广


得
(b2+a2k2)x2+2a2kqx+a2q2-a2b2=0.


问题的一般性结论为:
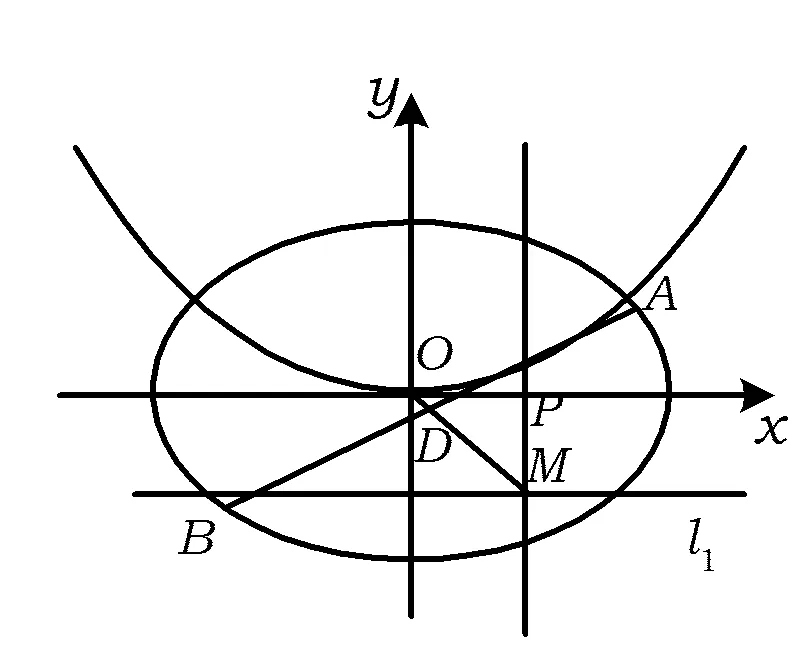
图2

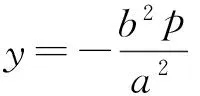
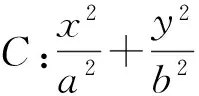
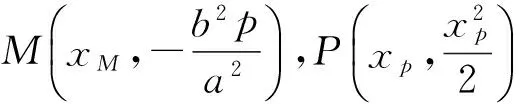
y=kx+q.
联立方程
得
(b2+a2k2)x2+2a2kqx+a2q2-a2b2=0,
可知



综合探究1、探究2可得如下的定理:

该结论道出了试题的深刻背景,也揭示出“动中有定,变与不变”的本质特征.命题者正是依据以上定理所蕴含的规律,利用特殊化,将其中的本质属性隐藏,命制出一道有一定思维难度、区分度较高、能较好考查学生数学素养的好题[3].
笔者在探究1和探究2的基础上进一步纵向深度探究和横向拓展,另有一番风味.
3 纵向探究
探究3探究1中在给定椭圆和抛物线焦点位置前提下,得出交点M在定直线上.试想,若椭圆和抛物线的焦点在坐标轴上位置发生变化,那么交点M是否仍在一条定直线上呢?
经探究,交点M仍在一条定直线上.但要注意,当椭圆和抛物线焦点位置不同时,条件“过点P且垂直于x轴的直线”和“过点P且垂直于y轴的直线”要与之对应.综合得到以下新结论:
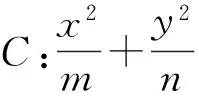

图3

证明过程如结论1,笔者不再赘述.最终的结论呈现出条件与结论的对应关系,展示了一种内在的对称美!
探究4将题中部分条件和结论互换后,命题是否成立?
推理论证后得到以下结论:
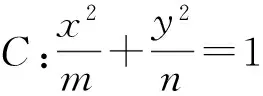
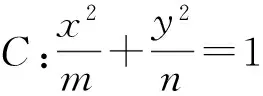
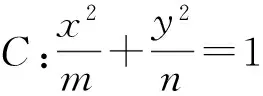
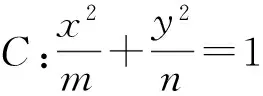

4 横向拓展
探究5椭圆的特例是圆,圆是椭圆的极限,那么以上结论是否成立?
结论1~2中作特殊化类比:令椭圆中m=n,即得:
结论7平面直角坐标系xOy中,⊙C:x2+y2=m(其中m>0),抛物线E:x2=2py(其中p>0).设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的2个点A,B,线段AB的中点为D,直线OD与过点P且垂直于x轴的直线交于点M,则点M在定直线y=-p上.
结论8平面直角坐标系xOy中,⊙C:x2+y2=m(其中m>0),抛物线E:y2=2px(其中p>0).设P是E上的动点,且位于第一象限,E在点P处的切线l与C交于不同的2个点A,B,线段AB的中点为D,直线OD与过点P且垂直于y轴的直线交于点M,则点M在定直线x=-p上.
同理,将定理1特殊化得:
定理2平面直角坐标系xOy中,⊙C:x2+y2=m(其中m>0),抛物线E:x2=2py(其中p>0).设P是E上的动点,且位于第一象限,过E上点P处的直线l若与C交于不同的2个点A,B,线段AB的中点为D,且直线OD与过点P且垂直于x轴的直线交于点M,则直线l为E在点P处的切线的充要条件是点M在定直线y=-p上.
将定理1在圆锥曲线内推广得:
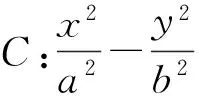
综合定理1~3,再推广,得到统一结论:

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2011.
[2]李锋.2014年高考数学福建卷理科第19题的探究历程[J].中国数学教育,2015(1/2):93-97.
[3]岳峻.透析考题信息提升解题驱动力——赏析2015年湖北卷21题[J].中学教研(数学),2015(8):30-32.
*收文日期:2016-06-23;2016-07-23
韩长峰(1979-),男,安徽阜阳人,中学一级教师.研究方向:数学教育.
O123.1
A
1003-6407(2016)09-43-04
