二元光滑函数芽在奇点处分岔解支数目的拓扑度公式

李　强，马丽丽

(齐齐哈尔大学理学院，黑龙江 齐齐哈尔 161006)



二元光滑函数芽在奇点处分岔解支数目的拓扑度公式

李强，马丽丽

(齐齐哈尔大学理学院，黑龙江 齐齐哈尔 161006)

讨论了二元光滑函数在奇点处的分岔解支数目问题.在孤立奇点的假设下，给出了通过拓扑度计算二元光滑函数芽的分支解数目的一个公式.

奇点；分岔解；拓扑度

0　引言

非线性方程解的存在性问题是非线性分析、微分方程、分歧理论等领域的重要研究课题.方程F(x)=0 的可能分歧点是F的奇点，根据奇点理论中映射芽的有限决定性方法，能够对可微分映射F进行分类，进而通过对与F强等价类的戈鲁比茨基-沙弗(GS)范式进行讨论，给予F在奇点附近的解的分歧问题以有力的回答.对于映射芽的强、弱决定性参见文献[1-2].

拓扑度理论是研究非线性算子定性理论的有力工具，它在研究奇重特征根所产生的分歧问题中有着十分重要的应用.本文主要考虑有限维空间上的拓扑度，即Brouwer度.Brouwer度的引入方式有很多，最早起源于代数拓扑中关于不动点的研究，之后在不同的角度建立了Brouwer度，但所得到的结果是一致的.

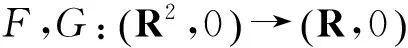
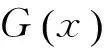
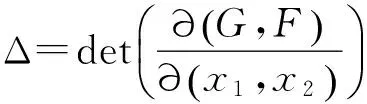
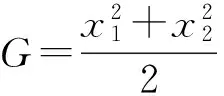
1　预备知识

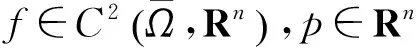
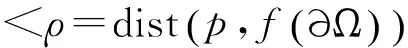
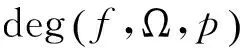
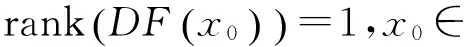
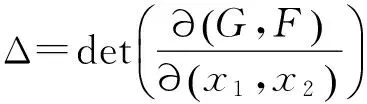
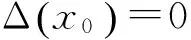
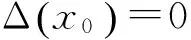
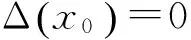
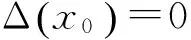
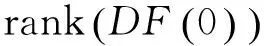
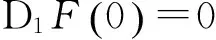
(1.1)

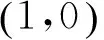
(1.2)

由于原点为函数G|N的临界点，则由(1.2)式有

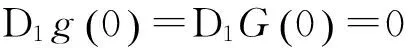
(1.3)

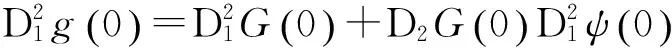
(1.4)

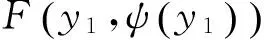
即

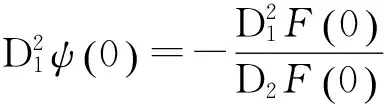
由(1.4)式，

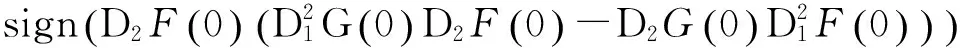
(1.5)

对任意的x∈U，

由(1.3)式得

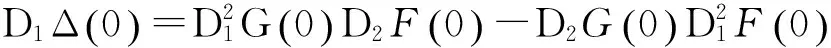
结合(1.1) 与(1.5)式得

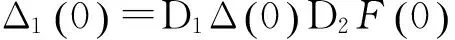
从而引理得证.

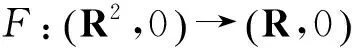
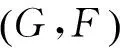
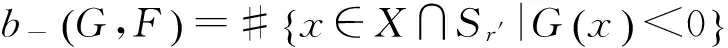
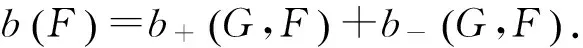
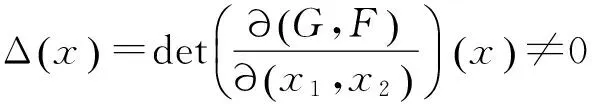
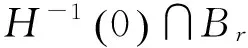
令M为1维带边紧流形，则M的边界∂M为有限集. 若G:M→R为光滑函数，设函数G在M内有有限个临界点，且均为非退化临界点. 记

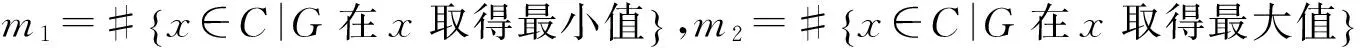
其中C表示G在M内的临界点集.

引理1.3设函数G满足如下条件：

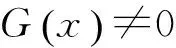
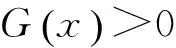
则有

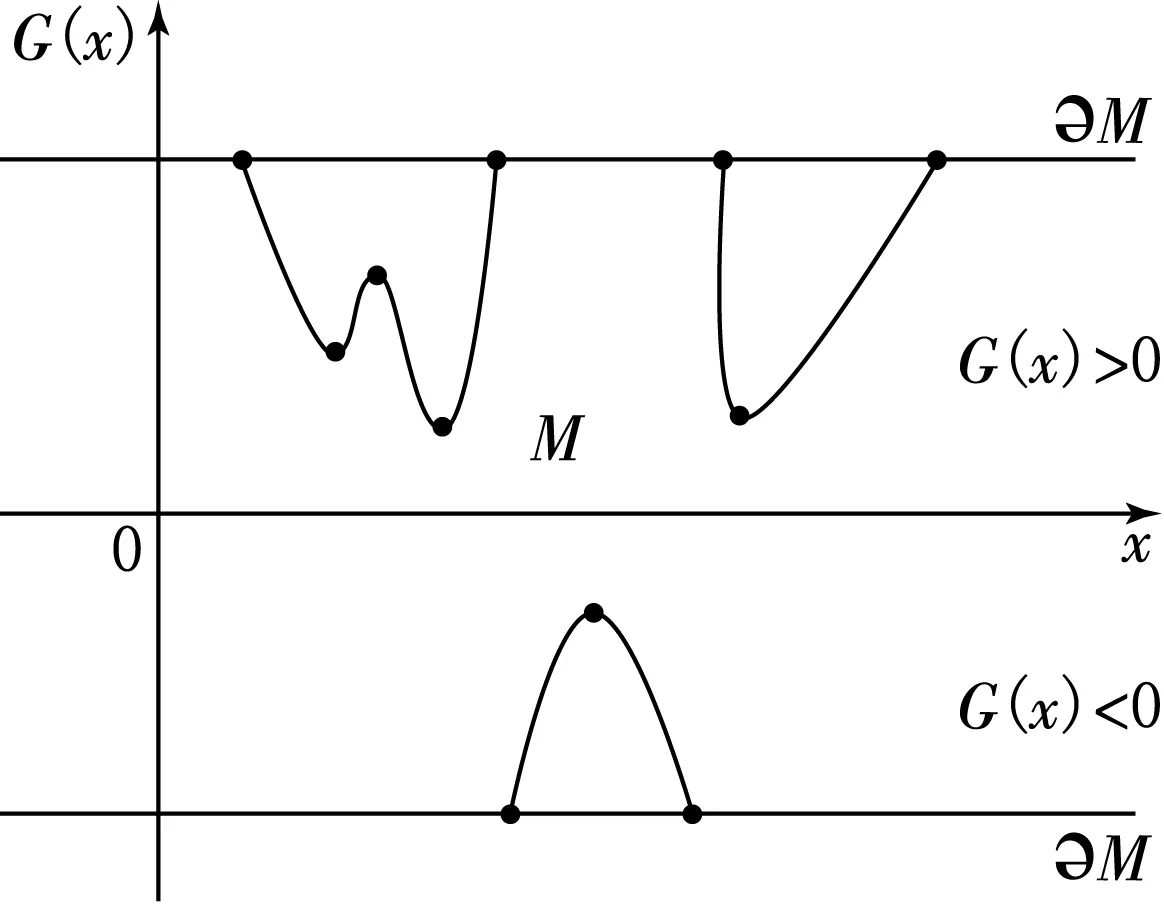
图1　引理1.3示意图

引理 1.3的示意图见图1.如图1所示，

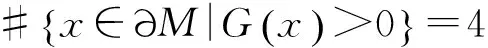
即

.

2　主要结果

对于前文所述的F，G，H及区域X，有如下计算公式.

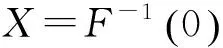
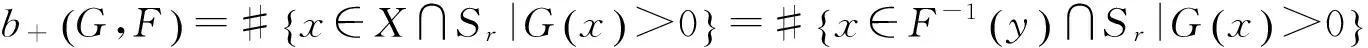
(2.1)

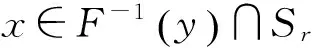
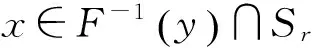
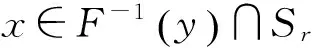
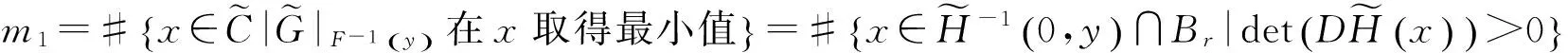
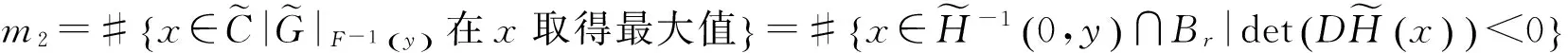
(2.2)

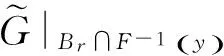
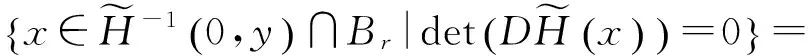
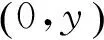
记d为映射x‖‖的Brouwer度，由拓扑度的定义及(2.2) 式，m1-m2=d. 显然，若y在原点临近且趋近于G，则，且于是函数满足引理 1.3 的条件，因而

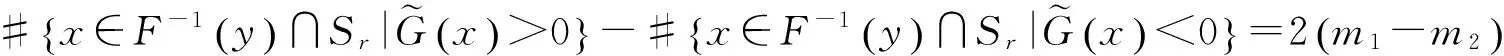
根据(2.1)式，

定理得证.

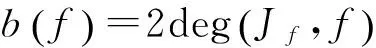
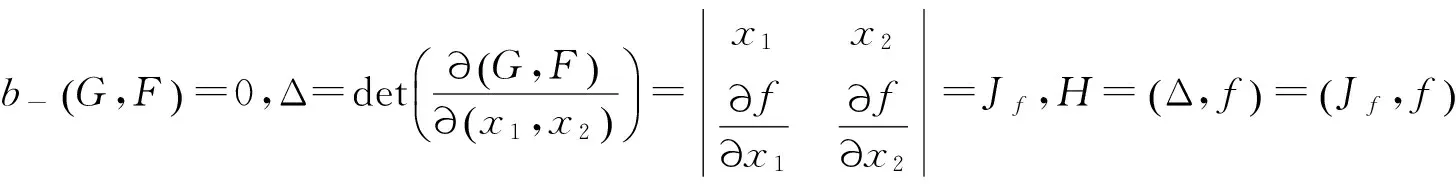
由定理2.1有

3　举例

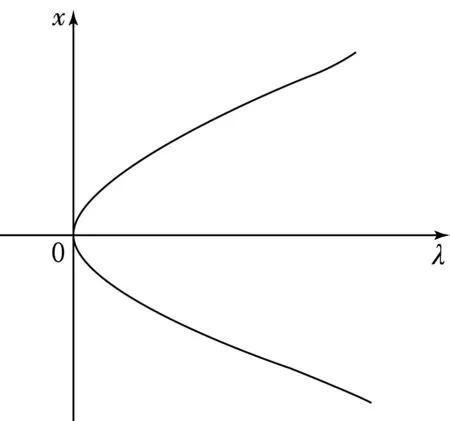
图的解曲线

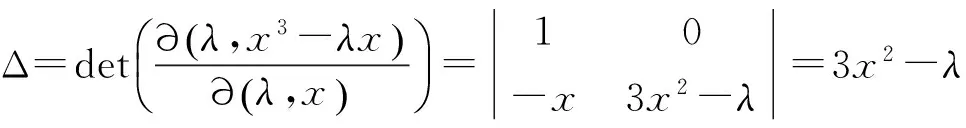
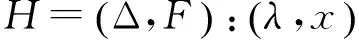
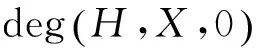
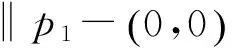
使得

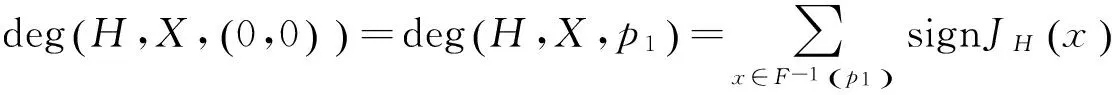
于是

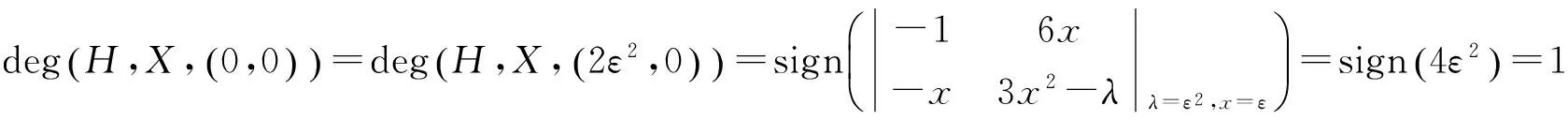
从而

[1]陈亮，孙伟志，裴东河. 映射芽的强相对有限决定性 [J]. 东北师大学报(自然科学版)，2004，36(4)：16-20.

[2]石昌梅，裴东河. 光滑函数芽的弱决定性 [J]. 东北师大学报(自然科学版)，2013，45(3)：1-4.

[3]周鹍. 奇点处分岔解支的数目问题 [J]. 应用数学和力学，1997，18(10)：905-909.

[4]FUKUDA T，AOKI K，SUN W Z. On the number of branches of a plane curve germ[J].Kodai Mathematical Journal，1986，9(2)：179-187.

[5]FUKUI T. An algebraic formula for a topological invariant of bifurcation of 1-parameter family of function-germs[J]. Stratifications，singularities，and differential equations，1990，55：45-54.

(责任编辑：李亚军)

A formula of topological degree for the number of bifurcation solutions of binaryC∞function germ singularities

LI Qiang，MA Li-li

(School of Science，Qiqihar University，Qiqihar 161006，China)

A formula of topological degree for computing the number of branches of binaryC∞function germs，which having an isolated singular point，is presented.

singularity;bifurcation solution;topological degree

1000-1832(2016)03-0030-05

2015-05-10

黑龙江省科学基金项目资助(QC2016008).

李强(1980—)，男，博士，讲师，主要从事基础数学研究.

O 177.5[学科代码]110·57

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.007