余ribbon Turaev π-代数

郭双建，张晓辉

(1.贵州财经大学数学与统计学院，贵州 贵阳 550025；2.曲阜师范大学数学科学学院，山东 曲阜 273165)



余ribbon Turaevπ-代数

郭双建1，张晓辉2

(1.贵州财经大学数学与统计学院，贵州 贵阳 550025；2.曲阜师范大学数学科学学院，山东 曲阜 273165)

讨论了Turaevπ-代数余模范畴中的pivotal群交叉结构和ribbon群交叉结构，引入余pivotal Turaevπ-代数和余ribbon Turaevπ-代数的定义，并分别给出Turaevπ-代数伴有余pivotal结构和余ribon结构的充要条件.

Turaevπ-代数；ribbon群交叉范畴；余ribbon结构；余pivotal结构

Hopfπ-(余)代数是拓扑学家Turaev于2000年研究三维流形在余链环上主π-丛的Hennings不变量时所引入的代数结构，该结构在量子场和向量丛中有着广泛的应用.[1-2]从拓扑角度看，它是将3维流形的量子不变量推广到带有映射同调类的3维流形上；[3]从范畴论的角度看，它是将张量范畴推广为群交叉张量范围，这类范畴可以诱导带有目标空间K(π,1)的3维同伦量子场；[4]从Hopf代数的角度看，即是将Hopf代数推广为Hopfπ-(余)代数.[5]2002年，Virelizer对Hopfπ-(余)代数做了较系统的研究.[6]2006年，Caenepeel与De Lombaerde从范畴论的角度，给出了Hopfπ-(余)代数的一种解读.[7]随后，王栓宏[8-10]，Zunino[11-13]等学者也相继对Turaevπ-(余)代数做了大量的相关工作.关于Turaevπ-(余)代数经典著作见文献[14-16]等.为了构造新的辫子交叉范畴，Van Daele与王栓宏在2008年引入了弱turaevπ-(余)代数的概念，同时推广了弱Hopf代数和Turaevπ-(余)代数.[17]这些概念的引入，对同类研究工作起到了奠基和推动作用.

本文在上述研究的基础上，考虑Turaevπ-代数上的余模范畴，引入余pivotal Turaevπ-代数和余ribbon Turaevπ-代数的定义，并由此分别给出Turaevπ-代数伴有余pivotal结构和余ribbon结构的充要条件.

1　预备知识

定义1[5-6]设π为群，其单位元为e.一个π-代数是指一族k-空间H={Hα}α∈π，伴有一族k-线性映射m={mα,β：Hα⊗Hβ→Hα β}α，β∈π(称为乘法)，和元素1H∈He(称为单位)，满足对任意的α，β，γ∈π，有

mαβ,γ(mα,β⊗idHγ)=mα,βγ(idHα⊗mβ,γ)，

mα,1(idHα⊗η)=idHα=m1,α(η⊗idHα).

对任意的α，β∈π，h∈Hα，ɡ∈Hβ，记hɡ=mα,β(h⊗ɡ).

定义2[5-6]一个π-代数H={Hα}α∈π被称为Hopfπ-代数，若每个(HαΔα，εα)均为k-余代数(称为H的第α分支)，且伴有如下结构：

(1) 乘法mα,β：Hα⊗Hβ→Hα β为余代数同态，即

Δα βmα,β=(mα⊗mβ)Δα β，

(1)

(εα⊗ξβ)=ξα βmα，β.

(2)

此处Δβ(ɡ)=ɡ(1,β)⊗ɡ(2,β)，其中h∈Hα，ɡ∈Hβ，l∈Hγ，α，β,γ∈π.

(2) 存在一族k-线性映射S={Sα：Hα→Hα-1}α∈π(称为对极)，满足

mα-1，α(Sα⊗idHα)Δα=εα11=mα，α-1(idHα⊗Sα)Δa.

(3)

其中h∈Hα，α∈π.

定义3[5-6]称Hopfπ-代数H为Turaevπ-代数，若存在一族余代数同构ξ={ξβ：Hα→Hβ αβ-1}(称为共轭或者交叉结构)，满足：

(1)ξ保持乘法.对任意的α,β,γ∈π，有ξβξγ=ξβγ：Hα→H(βγ)α(βγ)-1，特别地，ξ1|Hα=idα.

(2)ξ与m相容.对任意的β∈π，有ξβ(hɡ)=ξβ(h)ψβ(ɡ).

(3)ξ与单位元1H相容.对任意的β∈π，有ξβ(1)=1.

(4)ξ保持对极.ξβSα=Sβ α β-1ξβ.

定义4[5-6]设H={Hα}α∈G为一族余代数.一个右H-π-余模是指一族k-空间M={Mα}α∈π，使得每个Mα均为右Hα-余模.此时记其余模结构为ρMα：Mα→Hα⊗Mα，其中ρM={ρMα}α∈π.

采用Sweedler符号来进行元素描述：对于m∈Mα，记余模作用为

ρMα(m)=m(-1,α)⊗m(0,α).

若M={Mα}α∈π和N={Nα}α∈π均为H-π-余模，称一族映射f={fα：Mα→Nα}α∈π为π-余模同态，若对任意的α∈π，均有ρNαfα=(idHα⊗fα)ρMα.此时记H-π-余模范畴为MH，记其中的有限维余模子范畴为Corep(H).

定义5设π为群，e为π的单位元.设存在张量范畴(C,⊗，I，a,l,r)，C中存在一族以π为指标集的子范畴{Cα}a∈π，使得C为这族子范畴的无交并，且对任意的α,β∈π，当对象U∈Cα，V∈Cβ时，有U⊗V∈Cα β，则称C为π-分次张量范畴，简记为π-范畴.此时子范畴Cα称为C的α-分支.

定义6[13]称群交叉范畴C=(C，(·)*)为左rigid群交叉范畴，若C中容许左对偶，且满足下面两个条件：

(1) 设对象U∈Cα，则其左对偶U*为Cα-1中的对象；

(2) 共轭同构保持对偶关系，即对于β∈π，U∈C，有φβ(evU)=evφβ(U)，φβ(coevU)=coevφβ(U).其中ev为左赋值映射，coev为左余赋值映射.

类似地，可定义右rigid群交叉范畴.一个既为左rigid群交叉范畴又为右rigid群交叉范畴的张量范畴被称为rigid群交叉范畴.

设C为rigid范畴.X，Y∈C，ɡ：Y→X为态射.则ɡ的左转置映射ɡ*定义如下

于是此时可定义？*：X→X*，称之为左对偶函子.类似地，称*？：X→*X为右对偶函子.

定义7[13]称rigid群交叉范畴C=(C，(·)*)为pivotal群交叉范畴，若C中存在一族从共轭右对偶函子到左对偶函子的张量自然同构ϑU：U(*U)→U*(其中U为C中对象)，满足φα(ϑU)=ϑφα(U).

定义8[2]记C中从对象U到对象V的态射集为C(U,V).一个群交叉范畴C被称为凝子群交叉范畴，若C中存在一族同构c={cU,V∈C(U⊗V，(UV)⊗U)}U,V∈C，使得下列条件成立：

(1) 对任意的α∈G，f∈Cα(U，U′)，ɡ∈C(V，V′)，有((αɡ)⊗f)∘cU,V=cU′,V′∘(f⊗ɡ)；

(2) 对任意的U，V，W∈C，有

(3) 对任意的U，V∈C，α∈π，有φα(cU,V)=cφα(U)，φα(V).

定义9[4]称辫子rigid群交叉范畴C为ribbon群交叉范畴(或简称为ribbon群范畴)，若C存在自对偶扭曲，即存在一族同构θ={θU：U→UU}U∈C，满足下列条件：

(1)θ是自然的，即对任意的α∈π，φ∈Cα(U，V)，有

θV∘φ=(αφ)∘θU；

(G1)

(2) 对任意的U∈Cα，V∈Cβ，有

θU⊗V=cU⊗VV,UU∘cUU,VV∘(θU⊗θV)；

(G2)

(3) 对任意的U∈C，α∈π，有

φα(θU)=θφα(U)；

(G3)

(4) 对任意的U∈Cα，有

(idUU⊗θUU*)∘coevUU=(θU⊗idU*)∘coevU.

(G4)

2　Corep(H)中的pivotal群交叉结构

从本节开始，约定H={(Hα，Δα，εα，Sα，ξα)}α∈π为Turaevπ-代数.

对任意的V∈Corepα(H)，令V*=*V=homk(V，k)，分别定义Hα-1的余模作用：

f(0,α-1)(v)⊗f(1,α-1)=f(v(0,α))⊗Sα(v(1,α))，v∈V，f∈V*；

定义赋值映射和余赋值映射如下：

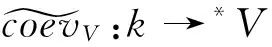
其中ei和ei为V的对偶基.易证如上定义的V*为V的左对偶，*V为V的右对偶，因此Corep(H)是一个rigid范畴.此时，易知上述定义的交叉结构φ与赋值映射之间的相容性条件是满足的，于是有如下命题.

命题1Corep(H)为rigid群交叉范畴.

J(U)=U(*U)，J(φ)=α(*φ).

则此时有集合同构Nat(F∘J，F∘?*)≅H*，其中?*为左对偶函子.

证明对任意的ϑ∈Nat(F∘J，F∘?*)，h∈Hα，定义映射A：Nat(F∘J，F∘?*)→H*如下

A(ϑ)={A(ϑ)α}α∈π，A(ϑ)α(h)∶=ϑHα(α(εα))(h).

对任意的ɡ={ɡα}α∈π∈H*，u∈U∈Corepα(H)，ψ∈*U，定义映射B：H*→Nat(F∘J，F∘?*)如下

B(f)={Q(ɡα)}α∈π，B(ɡα)U(αψ)(u)=ψ(u(0,α))ɡα(u(1,α)).

首先验证B定义的合理性.对任意的Corepα(H)中的态射φ：U→V，ν∈*V，u∈U，

(φ*∘B(ɡα)V)(αν)(u)=(B(ɡα)V(αν))(φ(u))=ν(φ(u(0,α)))ɡα(u(1,α))=

α(*φ(ν))α(u(0,α))ɡα(u(1,α))=(B(ɡα)U∘α(*φ))(αν)(u)，

即B(f)是自然变换，故B定义合理.

下证A和B互逆.一方面，A(B(ɡα))α(h)=B(ɡα)Hα(α(εα))(h)=ɡα(h)；另一方面，考虑到

B(A(ϑ)α)U(αψ)(u)=ψ(u(0,α))A(ϑ)α(u(1,α))=

ψ(u(0,α))ϑHα(α(εα))(u(1,α))=ϑHα(α(εα))(ψ(u(0,α))u(1,α)).

故只需证明ϑHα(α(εα))(ψ(u(0,α))u(1,α))=ϑU(αψ)(u)即可.为此，定义映射

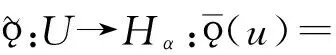
从而A和B互逆.

下设ϑ∈Nat(F∘J，F∘?*)和ɡ={ɡα}α∈π∈H*为在上述同构下互相对应的元素.

引理1ϑ为H-余线性的，当且仅当ɡ满足对任意的α∈π，a∈Hα，均有

(4)

证明充分性.对任意的u∈U∈Corepα(H)，ψ∈*U，

ϑU(α(ψ(0,α-1)))(u)⊗ξα(ψ(0,α-1))=ψ(0,α-1)(u(0,α))ɡα(u(1,α))ξα(ψ(0,α-1))=

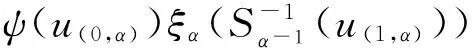
ϑU(α(ψ))(0,α-1)(u)⊗ϑU(α(ψ))(1,α-1)，

即ϑU为H-余线性的.

必要性.取U=Hα，εα=ψ，由ϑHα的余线性性质，直接可得到等式(4).

引理2ϑ同构，当且仅当ɡ卷积可逆.

证明充分性.设ɡ的卷积逆为ɡ-1.对任意的u∈U∈Corepα(H)，φ∈U*，定义自然变换ϑ′为

易知

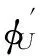
引理3ϑ为张量自然变换，当且仅当ɡ对任意的α，β∈π，a∈Hα，b∈Hβ，满足

ɡβ α(ba)=ɡα(a)ɡβ(b).

(5)

证明充分性.对任意的u∈U，v∈V,U∈Corepα(H),V∈Corepβ(H)，μ∈*U，ν∈*V，有

ϑU⊗V(βν⊗αμ)(v⊗u)=(βν⊗αμ)((v⊗u)(0,β α))ɡβ α((v⊗u)(1,β α))=

βν(v(0,β))αμ(u(0,α))ɡβ α(v(1,β)u(1,α))=βν(v(0,β))αμ(u(0,α))ɡβ(v(1,β))ɡα(u(1,α))=

(ϑV(βν)⊗ϑU(αμ))(v⊗u)=(ϑV⊗ϑU)(βν⊗αμ)(v⊗u).

即φ为张量自然变换.

必要性.取U=Hα，V=Hβ，μ=ξα，ν=εβ，由ϑ的张量性质，即可得到等式(5).

引理4对任意的α,β∈π，U∈Corepβ(H)，ϑ满足φα(ϑU)=ϑφα(U)，当且仅当ɡ对任意的α,β∈π，a∈Hα，β∈Hβ，

ɡβ(b)=ɡα β α-1(ξα(b)).

(6)

证明充分性.对任意的u∈U∈Corepβ(H)，φ∈U*，

φα(ϑU)(α βφ)(αu)=α(ϑU(βφ)(u))=φ(u(0,β))ɡβ(u(1,β))=

αφ(α(u(0,β)))ɡα β α-1(ξα(u(1,β)))=ϑα β φ(αu).

必要性.取U=Hβ，φ=εβ，即可知等式(6)成立.

定义10设H={Hα}α∈π为Turaevπ-代数.称线性型ɡ={ɡα}a∈π∈H*为H上的余pivotal结构，若ɡ为卷积可逆的，且满足等式(4)—(6).此时称H={(Hα，ɡα)}α∈π为一个余pivotal Turaevπ-代数.

例1若π=e，则易知此时H={(Hα，ɡα)}α∈π为一个余pivotal Hopf代数.

综上，由命题1—2，引理1—4，可得以下本文主要结果之一.

定理1设H={Hα}α∈π为Turaevπ-代数.则H为余pivotal Turaevπ-代数，当且仅当H的余表示范畴Corep(H)为pivotal群交叉范畴.

3　Corep(H)中的ribbon群交叉结构

由文献[9]可知，H={Hα}α∈π被称为余拟三角Turaevπ-代数，若存在k-线性映射σ={σβ,γ：Hβ⊗Hγ→k}β,γ∈π，使得对任意的β，γ，θ∈π，x∈Hβ，y∈Hγ，p∈Hθ，下列条件成立：

(C1)σβ，γθ(x，yp)=σβ，θ(x(1,β),p)σβ，γ(x(2,β),y)；

(C2)σβγ，θ(xy,p)=σβ，γθγ-1(x，ξγ(p(1,θ)))σγ，θ(y,p(2,θ))；

(C3)σβ，γ(x(1,β),y(1,γ))x(2,β)y(2,γ)=ξβ(y(1,γ))x(1,β)σβ，γ(x(2,β),y(2,γ))；

(C4)σβ，γ(x,y)=σθβθ-1，θγθ-1(ξθ(x),ξθ(y))；

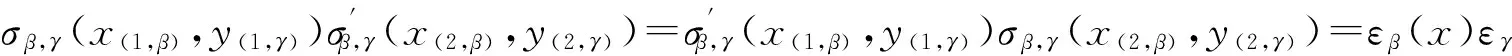
以下约定H={(Hα，σ)}α∈π为余拟三角Turaevπ-代数.

注2对任意的α，β∈π，由文献[9]中定理3.5，易知余拟三角结构可诱导余模范畴Corep(H)中的辫子结构cU,V为

I(U)=UU，I(φ)=αφ.

则此时有集合同构Nat(F，F∘I)≅H*.

证明对任意的θ∈Nat(F，F∘I)，h∈Hα，定义映射P：Nat(F，F∘I)→H*，

P(θ)={P(θ)α}α∈π，P(θ)α(h)∶=εαk(θHα(h)).

对任意f={fα}α∈π∈H*，u∈U∈Corepα(H)，定义映射Q：H*→Nat(F，F∘I)，

Q(f)={Q(fα)}α∈π，Q(fα)U(u)=fα(u(1,α))α(u(0,α)).

首先验证Q定义的合理性.对任意Corepα(H)中的态射φ：U→V，u∈U，有

Q((fα)V∘φ)(u)=fα((φ(u))(1,α))α((φ(u))(0,α))=

fα(u(1,α))(αφ(α(u(0,α))))=(αφ∘Q(fα)U)(u).

即Q(f)是自然变换，故Q定义合理.

下证P和Q互逆.一方面，我们有

P(Q(fα))α(h)=εα(Q(fα)H(h))=εα(fα(h(2,α))α(h(1,α)))=fα(h).

另一方面，因为

Q(P(θ)α)U(u)=(P(θ)α)(u(1,α))α(u(0,α))=εα(θHα(u(1,α)))α(u(0,α))，

故只需证明εα(θHα(u(1,α)))α(u(0,α))=θU(u)即可.为此，任取U*中的元素，并定义映射为

α(εα(θHα(u(1,α)))α(u(0,α)))=εα(θHα(u(1,α)))α(α(u(0,α)))=

εα(θHσk(

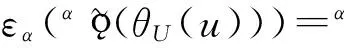
设θ∈Nat(F，F∘I)和f={fα}α∈π∈H*为在上述同构下互相对应的元素.由以上证明过程可知θ满足公式(G1).

引理5θ为H-余线性的，当且仅当f为共轭余交换的，即f满足对任意的α∈π，h∈Hα，均有fα(h(1,α))h(2,α)=ξα(h(1,α))fα(h(2,α)).

证明充分性.设α∈π，u∈U∈Corepα(H)，易知

(ρUU∘θU)(u)=fα(u(2,α))α(u(0,α))⊗ξα(u(1,α))=

fα(u(1,α))α(u(0,α))⊗u(2,α)=((θU⊗idHα)∘ρU)(u)，

于是θα为Hα-余线性的.

必要性.取U=Hα，由θα的余线性性质，对任意的h∈Hα，均有fα(h(3,α))α(h(1,α))⊗ξα(h(2,α))=fα(h(2,α))α(h(1,α))⊗h(3,α).两边同时以εα⊗id作用，即可知命题成立.

引理6θ为同构，当且仅当f为卷积可逆的.

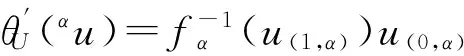
直接验证即可知θ′即为θ的逆元.

则类似于引理2，易证f′即f的卷积逆.

引理7θ满足公式(G2)，当且仅当f对任意的α,β∈π,a∈Hα，b∈Hβ，满足

σβ,α(ξβ(b(1,β))，a(1,α))σα,β(ξα(a(2,α))，ξβ(b(2,β)))fα(a(3,α))fβ(b(3,β))=fα β(ab).

(7)

证明充分性.对于α，β∈π，u∈U∈Corepα(H)，v∈V∈Corepβ(H)，

(cU⊗VV，UU∘cUU,VV∘(θU⊗θV))(u⊗v)=

(cU⊗VV,UU∘cUU,VV)(fα(u(1,α))fβ(v(1,β))α(u(0,α))⊗β(v(0,β)))=

cUU,VV(fα(u(2,α))fβ(v(2,β))σα,β(ξα(u(1,α))，ξβ(v(1,β)))α β(v(0,β))⊗α(u(0,α)))=

σα,β(ξα(u(2,α)),ξβ(v(2,β)))fα(u(3,α))fβ(v(3,β))σαβ α-1，α(ξα β(v(1,β))，ξα(u(1,α)))αβ α(u(0,α))⊗α β(v(0,β))=

σβ,α(ξβ(v(1,β))，u(1,α))σα,β(ξα(u(2,α)),ξβ(v(2,β)))fα(u(3,α))fβ(v(3,β))αβ α(u(0,α))⊗α β(v(0,β))=

fα β(u(1,α)v(1,β))αβ α(u(0,α))⊗α β(v(0,β))=θU⊗V(u⊗v)，

即公式(G2)成立.

必要性.取U=Hα，V=Hβ，在公式(G2)等号两边同时以(εαβ αβ-1α-1⊗εαβ α-1)作用，即可知结论成立.

引理8θ满足公式(G3)，当且仅当f对任意的α,β∈π,b∈Hβ，满足

fβ(b)=fαβ α-1(ξα(b)).

(8)

证明充分性.对任意的v∈V∈Corepβ(H)，

ξα(θV)(αv)=α(θV)(αv)=fβ(v(1,β))α β(v(0,β))=

fαβ α-1(ξα(v(1,β)))α β(v(0,β))=θαV(αv)，

即公式(G3)成立.

必要性.取V=Hβ，在公式(G3)等号两边同时以εαβ α-1作用，即可知结论成立.

引理9θ满足公式(G4)，当且仅当f对任意的α∈π，a∈Hα，满足

fa-1(ξα(Sα(a)))=fα(a).

证明充分性.对于α∈π，u∈U∈Corepα(H)，

((idUU⊗θUU*)∘coevUU)(1k)(u)=∑(idUU⊗θUU*)(αei⊗αei)(u)=

αu(0,α)fα-1(ξα(Sα(u(1,α))))=αu(0,α)fα(u(1,α))=

∑fa(ei(1,α))αei(0,α)⊗ei(u)=((θU⊗idU*)∘coevU)(1k)(u)，

即公式(G4)成立.

必要性.取U=Hα，在公式(G4)等号两边同时以εα作用，即可知结论成立.

定义11设H={Hα}α∈π为余拟三角Turaevπ-代数.称线性型f={fα}α∈π∈H*为H上的余ribbon结构，若f为共轭余可换的，卷积可逆，且满足等式(7)—(9).称H={(Hα,fα)}α∈π为一个余ribbon Turaevπ-代数.

例2若π=e，则易知此时H={(Hα，fα)}α∈π为一个余ribbon Hopf代数.

综上，由命题3及引理5—9，可得本文另一主要结果.

定理2设H={Hα}α∈π为余拟三角Turaevπ-代数.则H为余ribbon Turaevπ-代数，当且仅当H的余表示范畴Corep(H)为ribbon群交叉范畴.

[1]TURAEV V.Homotopy field theory in dimension 3 and crossed group-categories[J/OL].Arxiv：Math，2000[2015-01-18].arxiv.org/abs/math/0005291.

[2]董建伟，张又林.一维双极量子流体动力学等温模型稳态角的唯一性[J].东北师大学报(自然科学版)，2015，47(3)：33-36.

[3]TURAEV V.Homotopy field theory in dimension 2 and group-algebras[J/OL].Arxiv：Math，1999[2015-01-18].arxiv.org/abs/math/9910010.

[4]TURAEV V.Homotopy quantum field theory[M].Zurich：European Mathematical Society，2010：1-290.

[5]TURAEV V.Crossed group-categories[J].The Arabian Journal for Science and Engineering，2008，33(2C)：483-503.

[6]VIRELIZIER A.Hopf group-coalgebras[J].Journal of Pure and Applied Algebra，2002，171：75-122.

[7]CAENEPEEL S，DE LOMBAERDE M.A categorical approach th Turaev’s Hopf group-coalgebras[J].Communications in Algebra，2006，34：2631-2657.

[8]WANG S H.Group entwining structures and group coalgebra Galois extensions[J].Communications in Algebra，2004，32：3417-3436.

[9]WANG S H.Coquasitriangular Hopf group algebras and Drinfel’d co-doubles[J].Communications in Algebra，2009，35：77-101.

[10]WANG S H.Turaev group coalgebras and twisted Drinfeld double[J].Indiana University Mathematic Journal，2009，58(37)：1395-1417.

[11]ZUNINO M.Double construction for crossed Hopf coalgebras[J].Journal of Algebra，2004，278：43-75.

[12]ZUNINO M.Tannaka reconstruction for crossed Hopf group coalgebras[J/OL].Arxiv：Math，2006[2015-01-18].arxiv.org/abs/math/0606011v1.

[13]ZUNINO M.Yetter-Drinfeld modules for crossed structures[J].Journal of Pure and Applied Algebra，2004，193：313-343.

[14]CHEN Q G，WANG D G.The semisimplicity of weak Doi-Hopf modules[J].Acta Mathematica Sinica，Chinese Series，2014，57(3)：417-426.

[15]TURAEV V.Quantum invariants of knots and 3-manifolds[M].Berlin：De Gruyter，2010：1-605.

[16]YANG T，WANG S H.Constructing new braided T-categories over regular multiplier Hopf algebra[J].Communications in Algebra，2011，39：3073-3089.

[17]VAN DAELE A，WANG S H.New braided crossed categories and Drinfel’d quantum double for weak Hopf group coalgebras[J].Communications in Algebra，2008，36：2341-2386.

(责任编辑：李亚军)

Coribbon Turaevπ-algebras

GUO Shuang-jian1，ZHANG Xiao-hui2

(1.School of Mathematics and Statistics，Guizhou University of Finance and Economics，Guiyang 550025，China；2.School of Mathematical Sciences，Qufu Normal University，Qufu 273165，China)

The crossed ribbon structure and crossed pivotal structure inCorep(H) are studied，where the category ofπ-comodules over a Turaevπ-algebraH.The notions of a copivotal Turaevπ-algebra and a coribbon Turaevπ-algebra are introduced.Finally，the necessary and sufficient conditions forCorep(H) to be a crossed pivotal category and to be a crossed ribbon category are given.

Turaevπ-algebra；crossed ribbon category；coribbon structure；copivotal structure

1000-1832(2016)03-0014-07

2015-01-18

国家自然科学基金资助项目(11371088)；国家数学天元基金资助项目(11426073)；江苏省自然科学基金资助项目(BK2012736)；贵州省科技厅基金资助项目(2014GZ81365).

郭双建(1981—)，男，博士，副教授，主要从事Hopf代数及量子群研究；通信作者：张晓辉(1985—)，男，博士，讲师，主要从事Hopf代数及量子群研究.

O 153.3[学科代码]110·21

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.004