变系数KP方程和变系数广义KP方程的变速孤波解

李向正，王乔丹,张金良

(1.河南科技大学 数学与统计学院,河南 洛阳 471023;2.北京理工大学 自动化学院，北京 100081)



变系数KP方程和变系数广义KP方程的变速孤波解

李向正1，王乔丹2,张金良1

(1.河南科技大学 数学与统计学院,河南 洛阳 471023;2.北京理工大学 自动化学院，北京 100081)

根据简化齐次平衡原则，导出了一个齐二次方程的解到变系数KP方程解之间的非线性变换，由于该齐二次方程有指数函数形的解，因此根据非线性变换可得出变系数KP方程的变速孤波解，并把此结果推广到变系数广义KP方程的情形。

变系数KP方程；简化齐次平衡原则；孤波解

0　引言

非线性数学物理方程常被用来刻画重要的物理过程，涉及了数学中几乎所有主流分支，其中方程求解始终是研究热点之一。齐次平衡原则[1-5]作为获取非线性方程精确解的方法，获得了广泛的关注和发展，一些重要的方法如F展开法和(G′/G)-展开法，都是依据齐次平衡原则来确定解的表达式中的最高次幂项。在利用齐次平衡原则求解非线性数学物理方程的过程中，本文精炼了齐次平衡原则的一些步骤，得到了简化齐次平衡原则[6]的方法。

本文研究的一般变系数KP方程

[ut+f(t)(6uux+uxxx)]x+g(t)uyy=0

(1)

和一般变系数广义KP方程

[ut+f(t)(3(n+1)unux+uxxx)]x+g(t)uyy=0,

(2)

其中：f(t)和g(t)是变量t的可积函数。方程(2)中的n是正整数。当n=1时，方程(2)退化为方程(1)。

当f(t)=1，g(t)=3α2时，方程(1)和方程(2)分别转化为规范化的KP方程

(ut+6uux+uxxx)x+3α2uyy=0

和广义KP方程

[ut+3(n+1)unux+uxxx]x+3α2uyy=0。

KP方程是由前苏联物理学家Kadomtsev和Petviashvili在研究弱色散介质中的非线性波动理论时发现的。KP方程有着广泛的物理背景，在流体力学、等离子体物理和气体动力学等领域有重要的应用，可作为描述(2+1)-维浅水波和等离体中离子声波的模型方程。KP方程描述了弱振幅表面波的传播，即在其他方向增加一个小扰动后，在一个方向上的弱非线性和弱色散波的传播。许多学者对KP方程进行了广泛的研究[7-10]，而对变系数的情形研究相对较少。对常系数KP方程，有学者利用截断展开法和Backlund变换得到了广义KP方程的类孤波解；有学者利用扩展的双曲正切函数展开法，得到KP方程具有Painleve性质条件下的解。变系数KP方程比常系数KP方程能够更好地描述实际的表面波情况，能够处理宽度、深度及密度等不断变化时，表面波通过峡谷进入大海或海洋的具体情况。而对于变系数KP方程或变系数广义KP方程，一些常用的方法变得不再适用，发展变系数KP方程的求解方法就成了一个重要的问题。文献[9]通过修正CK直接方法，建立了常系数和变系数KP方程之间的等价变换，从而利用常系数方程的解得到变系数方程的解。文献[10]用(G’/G)-展开法求出了变系数广义KP方程的精确解。KP方程的形式较多，本文所研究变系数KP方程和变系数广义KP方程与文献[9-10]中方程的形式不同，求解方法也不同。

本文用简化齐次平衡原则[6]，导出变系数KP方程(1)的一个非线性变换，借此变换求出其变速孤波解。然后，将结果推广到变系数广义KP方程的情形。

1　非线性变换的导出

考虑方程(1)中uux和uxxx之间的齐次平衡[1-5](2m+1=m+3→m=2)，按照简化齐次平衡原则(用对数函数Alnφ取代HB方法中的F(φ))[6]，可设方程(1)的解具有如下形式：

u(x,y,t)=A(lnφ)xx，

(3)

其中：常数A和函数φ=φ(x,y,t)均待定。下面要确定常数A和函数φ=φ(x,y,t)，使式(3)精确地满足方程(1)。为此，将式(3)代入方程(1)的左端得：

[ut+f(t)(6uux+uxxx)]x+g(t)uyy=

A(lnφ)xxxt+f(t)6[A(lnφ)xxA(lnφ)xxx]x+f(t)A(lnφ)6x+g(t)A(lnφ)xxyy=

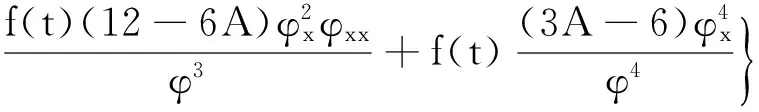
(4)

为确定常数A，置式(4)中φ-4的系数为0，则得A=2。将其代入式(3)及式(4),则式(3)和式(4)分别变为：

u(x,y,t)=2(lnφ)xx

(5)

和

[ut+f(t)(6uux+uxxx)]x+g(t)uyy=

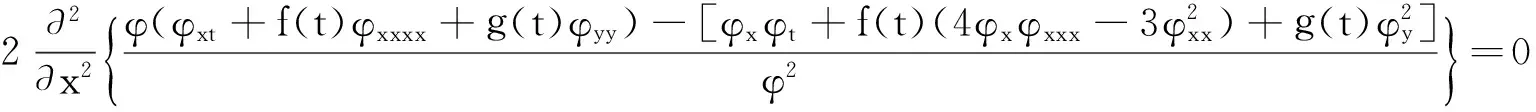
(6)

只要φ=φ(x,y,t)满足齐二次方程：

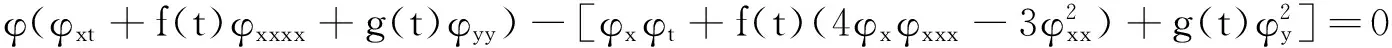
(7)

由式(5)、式(6)和方程(7)得出结论：若φ=φ(x,y,t)是齐二次方程(7)的一个解，将之代入式(5)，就得变系数KP方程的解。式(5)和方程(7)一起构成了齐二次方程(7)解到变系数KP方程(1)解的非线性变换。

2　齐次方程和变系数KP方程的解

由方程(7)的齐次性，可设其解具有如下形式：

φ(x,y,t)=1+eη,η=k(x+λy)+ω(t)，

(8)

ω(t)待定。将式(8)代入方程(7)的左端得：

eη(kω′+fk4+gk2λ2)+e2η(kω′+fk4+gk2λ2)-

e2η(kω′+fk4+gk2λ2)=eη(kω′+fk4+gk2λ2)=0。

只要ω=ω(t)满足常微分方程

kω′+fk4+gk2λ2=0，

解之得：

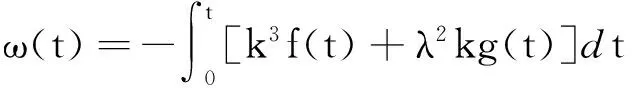
(9)

将式(9)代入式(8)，得方程(7)的解如下：

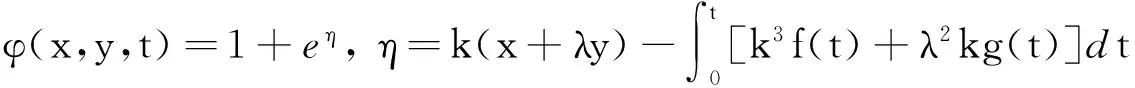
(10)

将式(10)代入式(5)，得变系数KP方程(1)的变速孤波解如下：

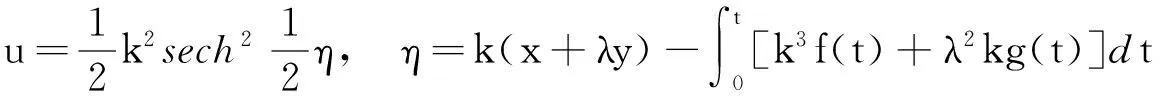
(11)

令η=const,关于t求导得波速如下：

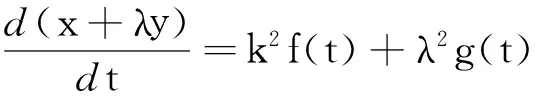
波速依赖于方程的系数，从而随变量t变化而变化。

3　变系数广义KP方程的解

为了将变系数KP方程结果推广到变系数广义KP方程的情形，引入广义行波变量：

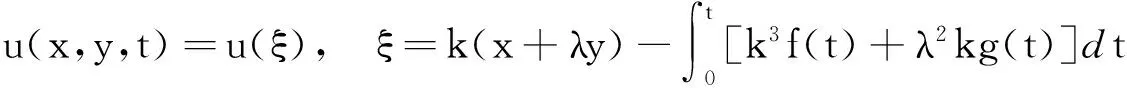
(12)

将式(12)代入变系数广义KP方程(2)，再将含有f(t)的项合并在一起，而含有g(t)的项相互抵消，并消去非零因子f(t)，则得u=u(ξ)的常微分方程：

-k4u″+(3k(n+1)unu′+k3u‴)′k=0。

(13)

关于ξ积分常微分方程(13)两次，取积分常数为0,则常微分方程(13)简化为：

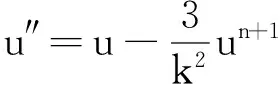
(14)

在文献[11]中，讨论了如下的非线性常微分方程：

u″=Au+Bun+1，

(15)

其解为：

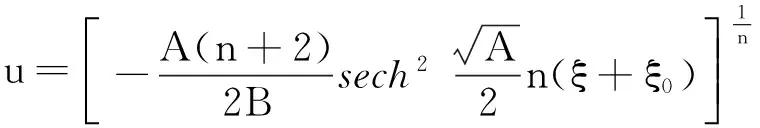
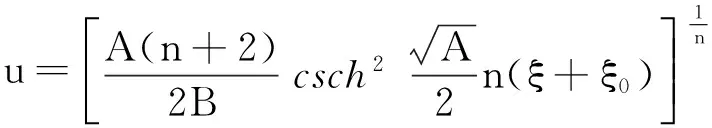
显然方程(14)是方程(15)的成员之一。利用方程(15)的结果，可得方程(14)的解如下：

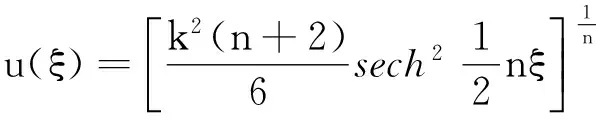
(16)

将式(16)代入式(12)得变系数广义KP方程的线孤波解：

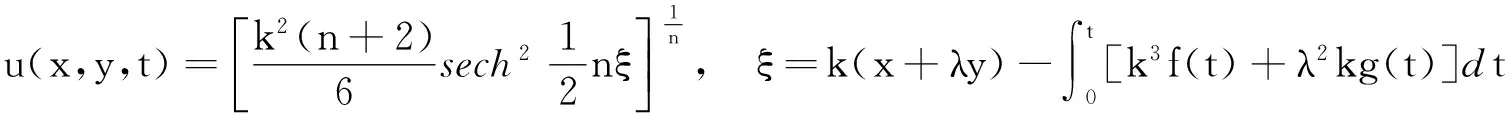
(17)

特别地，当n=1时，式(17)退化为变系数KP方程的线孤波解(11)。

4　结束语

本文用简化齐次平衡原则求解了变系数KP方程，所得变速孤波解的波速依赖于方程的系数，随变量t变化而变化。在此基础上，引入广义行波变量，将变系数广义KP方程化为简单可解的非线性常微分方程，从而借助已有研究成果,得到了该方程的线孤波解。解的形式(3)还可以改写为u(x,y,t)=A(lnφ)xx+lnφ关于x的低于2阶偏导数的适当线性组合，从而得到的齐次方程也与方程(5)有所不同，从齐次方程中找出更多有意义的解，从而可以找出变系数KP方程的一些新形式的精确解。

致谢:本文得到王明亮教授的指导，在此表示感谢。

[1]WANG M L.Solitary wave solutions for variant Boussinesq equations[J].Physics letters a,1995,199:169-172.

[2]WANG M L,ZHOU Y B,LI Z B.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Physics letters a,1996,216:67-75.

[3]李向正.Sawada-Kotera方程的两类孤立波解[J].河南科技大学学报(自然科学版),2014,35(2):78-81.

[4]李保安,李灵晓.简化变形Ostrovsky方程的精确解[J].河南科技大学学报(自然科学版),2014,35(2):82-85.

[5]李伟,张金良.变形Boussinesq方程组的精确解[J].河南科技大学学报(自然科学版),2016,37(2):92-95.

[6]WANG M L,LI X Z.Simplified homogeneous balance method and its applications to the Whitham-Broer-Kaup model equations[J].Journal of applied mathematics and physics,2014,2:823-827.

[7]ABLOWITZ M J,CLARKSON P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1991.

[8]INFELD E,ROWLANDS G.Nonlinear waves,solitons and chaos[M].Cambridge:Cambridge University Press,2001.

[9]王岗伟,刘希强,张颖元.变系数KP方程的新精确解[J].河北师范大学学报(自然科学版),2012,36(6):555-559.

[10]郭冠平.G’/G展开法求解变系数KP方程的精确解[J].浙江师范大学学报(自然科学版),2013,36(2):166-171.

[11]WANG M L,LI X Z.Exact solitary wave solutions of nonlinear evolution equations with a positive real number power term[J].International journal of nonlinear science,2015,19(2):67-80.

国家自然科学基金项目(10871129);河南科技大学博士启动基金项目(09001562)

李向正(1972-),男,河南偃师人,副教授,博士,主要研究方向为非线性数学物理方程.

2016-05-24

1672-6871(2016)06-0082-03

10.15926/j.cnki.issn1672-6871.2016.06.017

O175.2

A