基于改进K次短路径算法的有效路径搜索算法及实现
2016-09-22郑贵省李月明车亚辉
郑贵省,王 元,王 鹏,李月明,车亚辉
(1.军事交通学院 基础部,天津300161; 2.军事交通学院 研究生管理大队,天津300161)
基于改进K次短路径算法的有效路径搜索算法及实现
郑贵省1,王元2,王鹏2,李月明2,车亚辉2
(1.军事交通学院 基础部,天津300161; 2.军事交通学院 研究生管理大队,天津300161)
为提高有效路径搜索效率,结合ArcGIS具有的路径分析功能,以K次短路径算法为基础,依据重叠惩罚算法的原理,提出基于改进K次短路径算法的有效路径搜索算法。以ArcGIS为平台,给出了算法的实现方法。经过对实际路网的可视化测试,验证了改进算法具有较高的运行效率,为有效路径相关理论在ArcGIS平台的应用提供了一种技术手段和方法。
有效路径;K次短路径算法;GIS
路网中有效路径的计算方法是交通规划中交通流分配的关键技术。现有的有效路径计算方法很多,主要有启发式的定向搜索算法[1]、分层定向搜索算法[2]、基于层次空间推理的搜索算法[3],以及文献[4-5]提出的K次短路径算法、遍历算法等。虽然相关理论研究很多,但对算法效率和实现方面的研究较少。
地理信息系统(geographic information system,GIS)集数据管理、可视化和空间分析于一体,在诸多领域(尤其是交通领域)得到了广泛应用。路网具有很强的地理分布特性,基于GIS技术的优势,实现大规模实际路网中有效路径的快速搜索,是有效路径理论得以实际应用的必然趋势。现有GIS平台中的空间网络分析功能不断强化,已经可以实现实际路网中的最近设施点分析、服务区分析、选址等问题,如何结合其强大的空间分析功能和数据处理能力来实现其有效路径的搜索功能,将是需要研究的问题。
1 有效路径的定义
有效路径的定义方法很多,比较有代表性的有区间阻抗下的有效路径[6]、基于影响度的有效路径[7]和根据路径选择的因素提出的改进Dail有效路径[8]。常用的有效路径[9]定义方法如下:
若OD对(r,s)之间的路径k为有效路径,则需满足:
(1)k为简单无环路径;
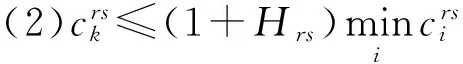
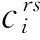
Hrs与实际路网情况和交通需求量有关,要进行深入分析才能确定。有关学者根据实际交通流数据对不同地区内有效路径的伸展系数进行了研究。文献[10]根据实际调查数据确定山东省高速公路网的伸展系数为0.3。现有研究也表明,路径选择行为会受到行驶距离的影响,因此有效路径伸展系数并非单一的绝对值。文献[11]考虑行驶里程的影响,采用“绝对差”与“相对差”结合的方式来确定河南省高速公路有效路径阻抗(行驶里程)的取值范围(见表1),其中L为最短路径里程。本文的有效路径取值范围也根据表1确定。

表1 有效路径的划分标准
2 基于改进K次短路径的有效路径搜索算法
针对现有的有效路径搜索算法,结合GIS具有的路径分析功能,从可实现的角度出发,主要考虑K次短路径算法来实现有效路径的搜索。K次短路径算法是按最短路、次短路、再下一条次短路的顺序产生K条路径集合的算法,具体算法有很多,它可以识别所有的有效路径。但是,K次短路径算法的时间复杂度很高。现有研究表明,与最短路径行驶时间差在20%的路径有几千条,会导致算法的执行时间过长。此外,识别出的有效路径之间相似程度很高,对实际情况而言也没有必要。因此,需要对K次短路径算法进一步改进。
重叠惩罚算法是一种用于计算合理多路径的算法,其基本原理是在每一次循环中,通过重叠惩罚函数来改变已经辨识出的路径中的路段阻抗,再采用最短路径算法来计算下一条有效路径。重叠惩罚算法原理简单,得到的路径差异较大,一般仅用来给出几条合理路径作参考。可以考虑结合重叠惩罚算法的原理来改进K次短路径算法,从而建立新的有效路径搜索算法。基本思想是在保证搜索效果的前提下,在K次短路径的循环中,按照重叠惩罚算法的基本原理来改变当前路径中的路段权重,从而达到降低计算出的有效路径之间的相似程度、提高搜索效率的目的。
定义原始法表示的实际路网为G=(V,E,W);n为节点个数,n=|V|;m为边个数,m=|E|。其中:V={v1,v2,…,vn}为节点集;vs为起点;vt为终点;E为边集;W={wij|(vi,vj)∈E}为边的权集,在此表示各路段的里程。所有有效路径可表示为{P|L(p)≤L′,p∈R},R为从vs到vt的所有路径,L(p)为路径p的行驶里程。
2.1基于K次短路径算法的有效路径搜索算法
K次短路径(K shortest paths,KSP)问题,本文具体为限定无环问题,通过有效路径的条件依次筛选出所有的有效路径,即可得到有效路径集。现有的K次最短路径算法主要有基于Dijkstra算法而产生的改进算法和基于Yen算法的改进算法[12]。在实际应用中,最广泛研究和采用的算法为Yen算法及其各种改进算法。Yen算法又称为偏离路径算法,是由Yen于1971年提出,其基本思想是从最短路径开始,循环利用当前求得最短路径来产生下一条次短路径,相关的改进算法主要改进了偏离路径的计算和获取,有MPS算法、DFS算法等。文献[13]对以上几种算法的效率进行了实验比较,发现MPS算法和DFS算法具有较高的时间效率,DFS算法虽然与MPS算法相比具有更高存储效率,但在应用中需提前知道K值,不满足应用条件。MPS算法和Yen算法的区别在于MPS算法采用偏离边的缩小长度来替代候选路径的长度。虽然MPS算法具有一定的时间优势,但GIS已提供最短路径的分析功能,且可以直接获得路径长度,因此,在GIS平台上,采用Yen算法来实现K次短路经算法更为方便。基于Yen算法的有效路径搜索算法的步骤如下。
(1)基于最短路径算法——Dijkstra算法,得到第一条最短路径p1,放入数组A中,并根据第一条最短路径的行程里程L(p1),确定有效路径里程最大值为L′。
(2)根据p1生成p2的候选路径集Q(初始为空),其计算过程为
(a)从G中删除一条边(vi,vj)∈p1;
(b)计算从vi到vt的最短路径为r,且r不通过p1从vi到vt之间的任何节点,由p1上从vs到vi的路径和r组成一条候选路径p,将路径p加入数组Q中,节点vi为p的偏离节点dev(p);
(c)恢复边(vi,vj),返回(a),删除p1中的另一条边,直到计算完p1中所有的边。
(3)令i=2。
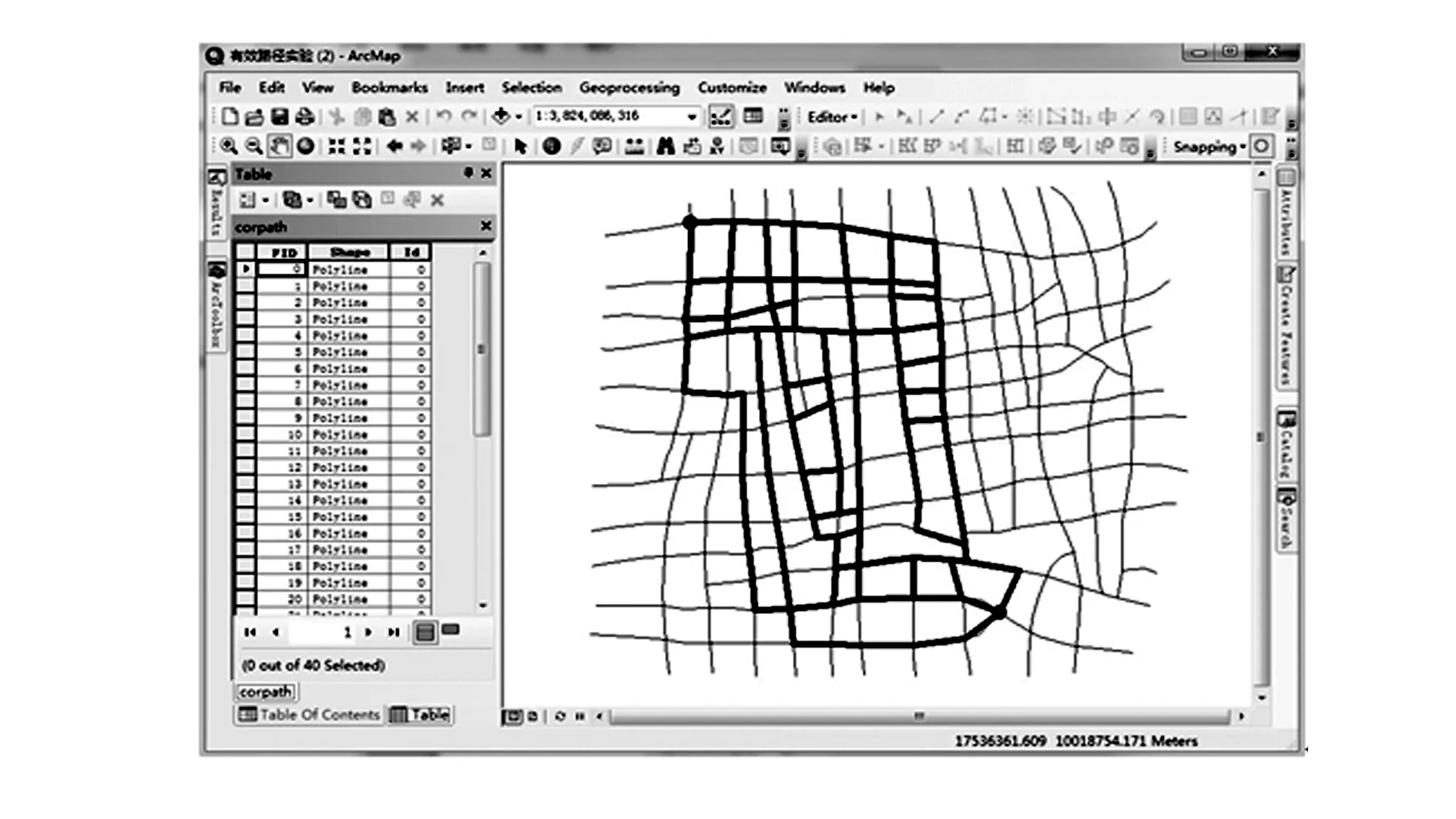
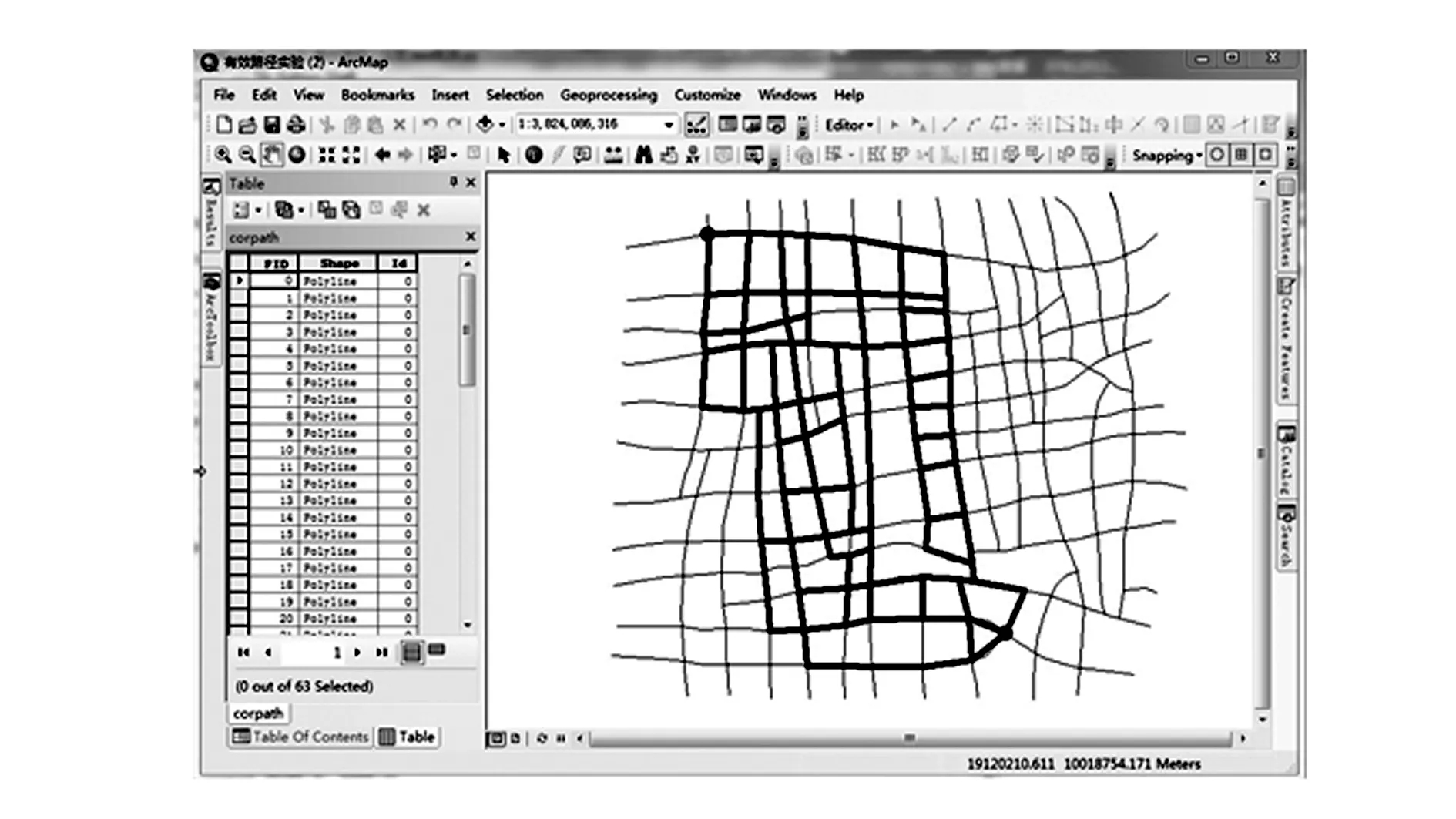
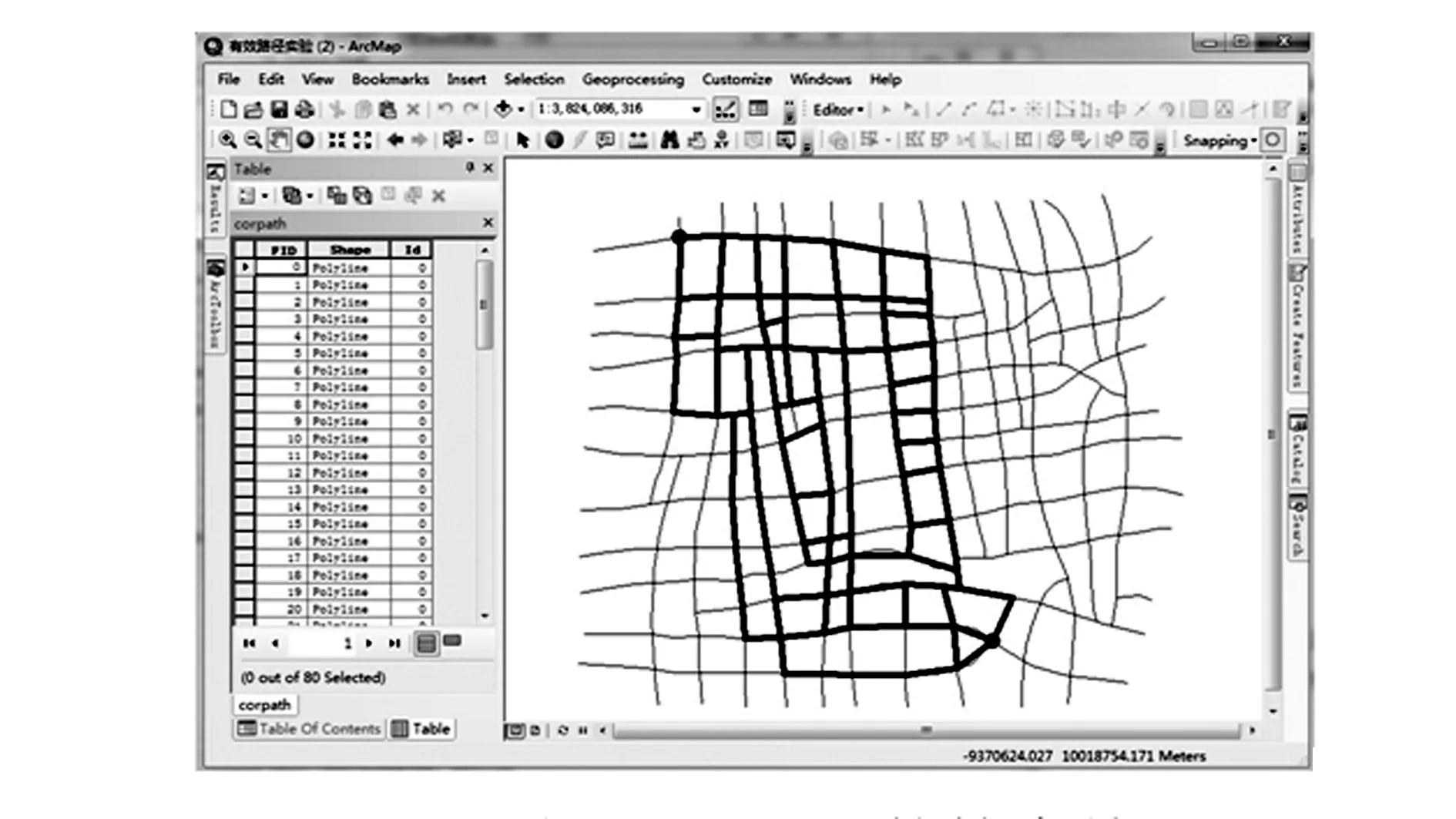
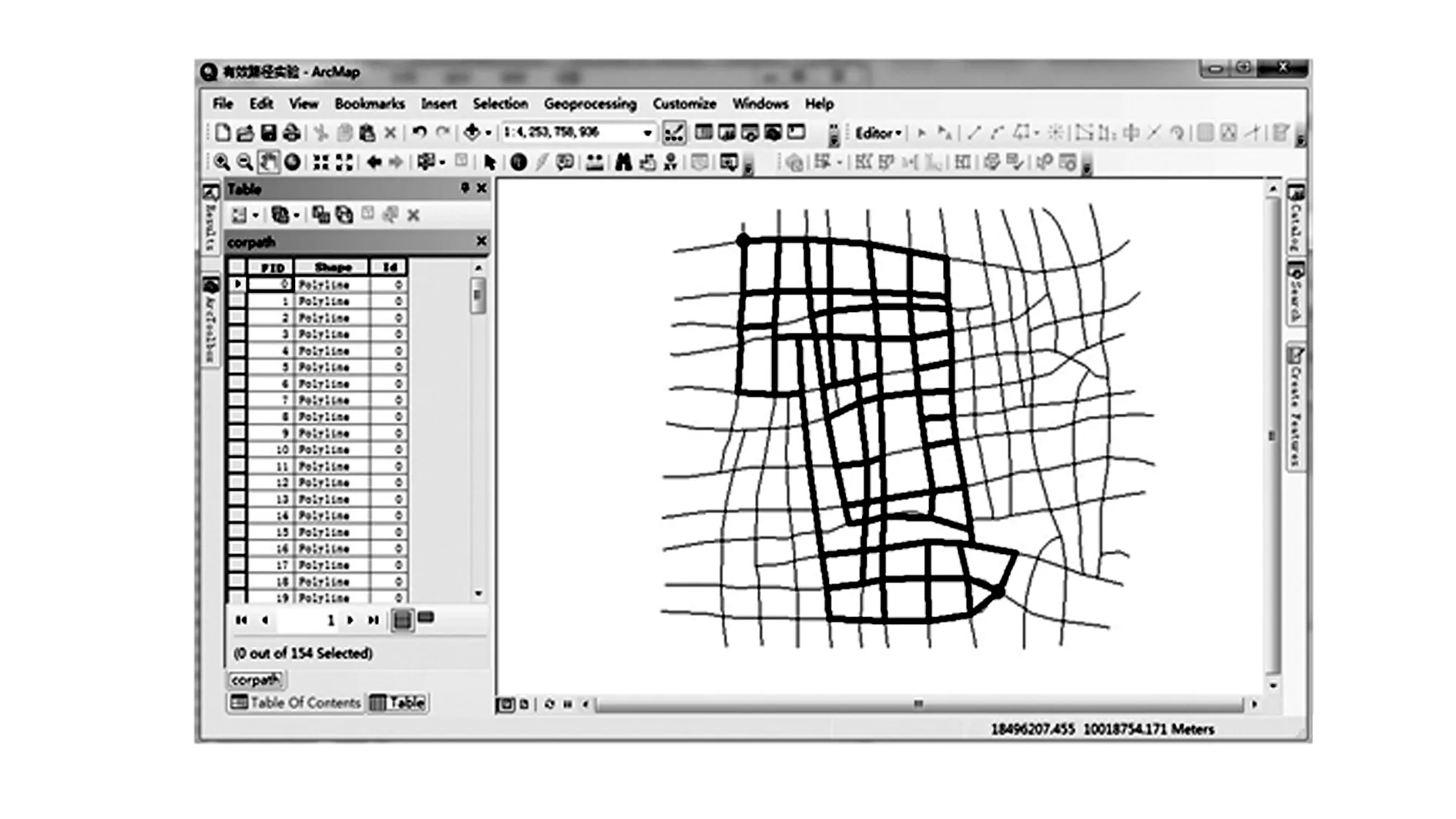
(4)令Q中最短的路径为pi,如果L(pi)>L′,则算法结束,A即为有效路径的集合;否则,从Q中移除pi,放入A中,并按照生成候选路径的方法由pi产生新的候选路径集放入Q中。在生成候选路径集的过程中,除了依次删除pi上的边之外,还要删除之前的pj(j (5)i=i+1,返回(4)。 2.2基于改进K次短路径算法的有效路径搜索算法 主要通过改进Yen算法中的(2)和(4)来建立新的有效路径搜索算法,改进后的算法步骤如下。 (1)基于最短路径算法——Dijkstra算法,得到第一条最短路径p1,放入数组A中,并根据第一条最短路径的行程里程L(p1),确定有效路径里程最大值为L′。 (a)从G中删除一条边(vi,vj)∈p1; (b)计算从vi到vt的最短路径为r,且r不通过p1上从vs到vi之间的任何节点,由p1上从vs到vi的路径和r组成一条候选路径p,将路径p加入数组Q中,节点vi为p的偏离节点dev(p); (c)恢复边(vi,vj),返回(a),删除p1中的另一条边,直到计算完p1中所有的边。 (3)令i=2。 (5)i=i+1,返回(4)。 算法的流程如图1所示。 图1 算法流程 如图2所示为某地区的密度较大的公路网局部,包含366条边和236个节点,假设路网中有两个节点为交通流的起讫点(图中标志出的两个节点,节点1为起点,节点2为终点),分别采用以上两种搜索算法,通过Python语言编程来搜索有效路径,搜索结果在GIS平台上可视化表示。由于K次短路径算法的时间复杂度过高,为测试比较两种算法的效率,假设有效路径里程的取值范围为(L,1.1L),其中,L为起讫点之间的最短路径里程。 图2 测试路网(局部) 以ArcGIS10.2软件中的ArcMap10.2为GIS平台,采用ArcGIS的脚本语言Python作为编程语言,程序编写平台为PythonWin。ArcGIS专门为Python提供了站点包Arcpy,可与ArcGIS中的地理数据库进行直接交互,也可直接调用ArcGIS中已有的各种分析功能。同时, Python的复杂网络分析库networkx也提供了很多网络分析方面的算法库。 3.1基于K次短路径算法的测试结果 采用K次短路径算法来搜索有效路径,结果如图3所示。程序执行时间为7 842.30 s,搜索出的有效路径共10 654条。 图3 基于K次短路径搜索算法的有效路径搜索结果 3.2基于改进K次短路径算法的测试结果 算法中首先要确定惩罚系数α的取值,其取值范围一般为(0,1)之间。α取值过大会导致遗漏的有效路径过多,搜索结果不合理;α取值过小,则导致路径相似程度过高,程序执行时间过长。需要通过一定的实验来确定α的合理取值。 从出行的习惯上看,当人们沿路线前进时,总是希望能比当前位置更加接近出行的目的地,所以,终点比起点更靠近出行终点的路段一般属于有效路径。基于此,从搜索结果看,α的合理取值一般能达到保留所有终点比起点更靠近出行终点的路段即可。分别取α为(0.20,0.15,0.10,0.05,0.01),经过实验测试,相关测试数据见表2,有效路径搜索结果可视化表示如图4—8所示。 表2 不同α取值下算法的测试数据 图4 α=0.20的搜索结果 图5 α=0.15的搜索结果 由以上测试结果可知,基于改进K次短路径算法的有效路径搜索算法,在效率上具有明显优势,且可排除由K次短路径算法产生的许多不必要路径。对比图4—8可知,α取值分别为0.05和0.01时,基本满足包括所有终点比起点更靠近出行终点的路段的要求。同时,对比α取0.05和0.01时的测试数据,初步确定在实际路网中α取值为0.05时,产生的有效路径数目合理且程序运行效率较高。 图6 α=0.10的搜索结果 图7 α=0.05的搜索结果 图8 α=0.01的搜索结果 以K次短路径算法为基础,结合GIS所具有的路径分析功能,提出在GIS环境下可实现的有效路径搜索算法——基于改进K次短路径算法的有效路径搜索算法。以ArcGIS软件为GIS平台,Python为脚本语言,以实际路网为对象,对所提出的算法进行了实验,并初步确定了实际路网中惩罚系数的合理取值。实验结果证明,基于改进K次短路径算法的有效路径搜索算法,大大提高了有效路径的搜索效率。同时,算法在ArcGIS平台上的实现方法,能为有效路径相关理论在ArcGIS中的应用提供一定的技术手段和方法。 [1]何胜学,范炳全.随机交通分配中有效路径的搜索算法[J].交通与计算机,2005,23(5):38-41. [2]何胜学,范炳全.基于有效路径的交通流博弈分配算法[J].交通运输系统工程与信息,2007,7(1):115-119. [3]何胜学,范炳全.基于定向层次空间推理的有效路径搜索算法[J].交通运输系统工程与信息,2006,6(2):66-71. [4]杨群,关伟,张国伍.基于合理多路径的路径选择方法的研究[J].管理工程学报,2002(4):42-45. [5]赖树坤,姚宪辉,彭愚.交通网络中有效路径确定方法的探讨[J].交通标准化,2008(1):137-138. [6]周和平,王芳,成军.区间阻抗下的多路径交通分配[J].长沙理工大学学报,2014,11(3):1-5. [7]杨信丰,刘兰芬,李引珍,等.基于影响度的有效路径集合的确定[J].交通运输系统工程与信息,2011,11(6):104-110. [8]秦鸣,姜培.基于有效路径的多路径交通流分配[J].交通标准化,2010(4):30-32. [9]李志纯,黄海军.随机交通分配中有效路径的确定方法[J].交通运输系统工程与信息,2003,3(1):28-32. [10]张建勇,李成江,黄汝存.联网高速公路有效路径伸展系数[J].公路交通科技,2008,25(1):116-119. [11]张洋,彭利人,吕培建.合理多路径的确定方法与划分标准[J].中国交通信息产业,2007(5):48-52. [12]白轶多,胡鹏,夏兰芳.关于K次最短路径问题的分析与求解[J].武汉大学学报,2009,34(4):492-494. [13]GANG Feng. Improving space efficiency with path length prediction for finding K shortest simple path[J]. IEEE Transaction on Computers, 2014:2459-2472. (编辑:张峰) Algorithm of Efficient Path Searching and Its Implementation by Improving K Shortest Path Algorithm ZHENG Guixing1, WANG Yuan2, WANG Peng2,LI Yueming2, CHE Yahui2 (1. General Course Department, Military Transportation University, Tianjin 300161, China; 2. Postgarduate Training Brigade, Military Transportation University, Tianjin 300161, China) Aimed to obtain the most efficient paths within the shortest time, by employing the analytic founction of ArcGIS and the algorithm of overlapping penalty, this paper improves K shortest path algorithm and comes up with an efficient path searching algorithm which is implemented on ArcGIS platform and proved in road network visual tests to be effective and applicable. effective path; K shortest path algorithm; GIS 2015- 08-31; 2015-10-26. 郑贵省(1975—),男,博士,副教授,硕士研究生导师. 10.16807/j.cnki.12-1372/e.2016.04.020 U491.1 A 1674-2192(2016)04- 0080- 05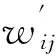
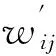
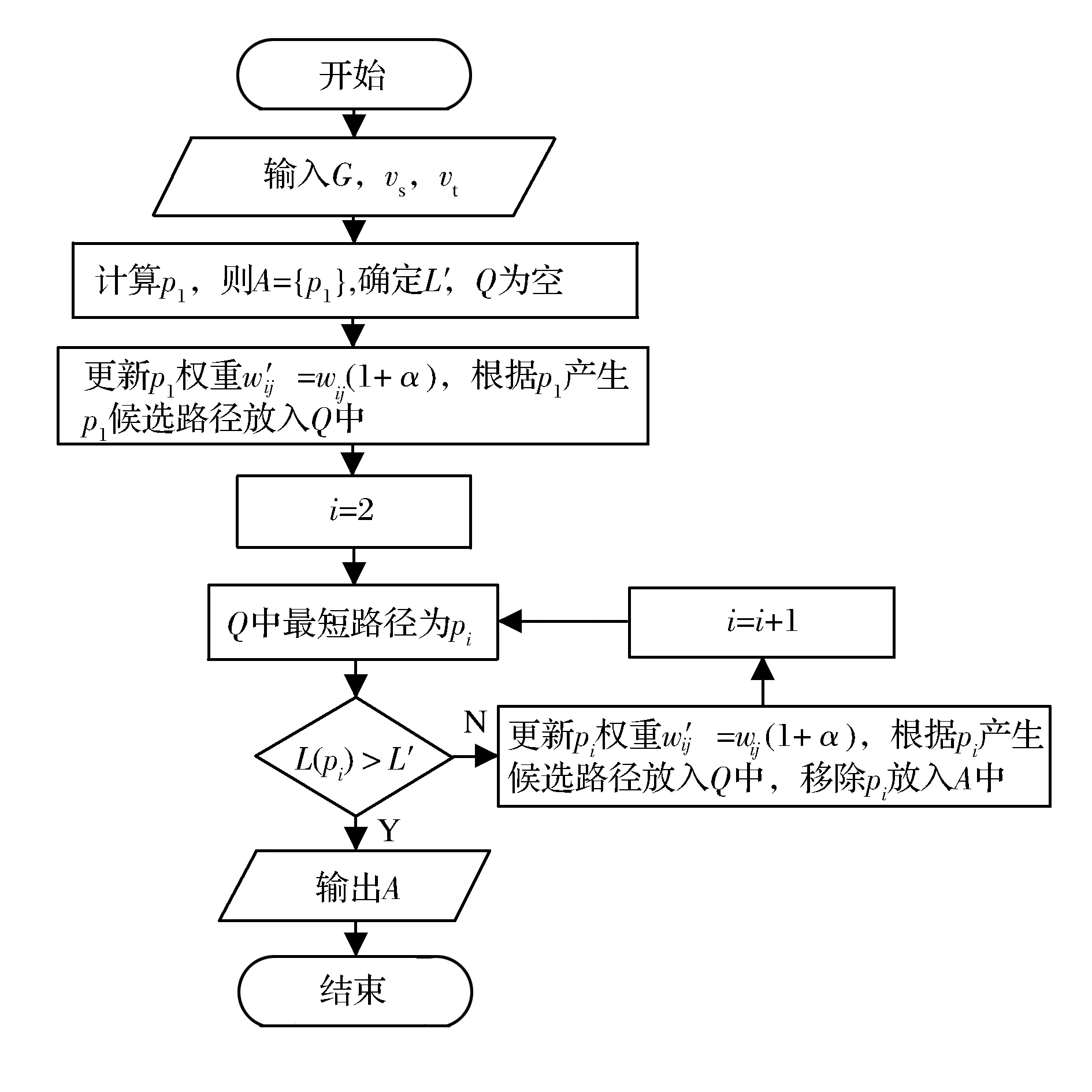
3 算法的实现及实例测试
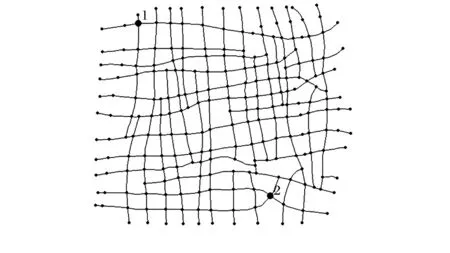
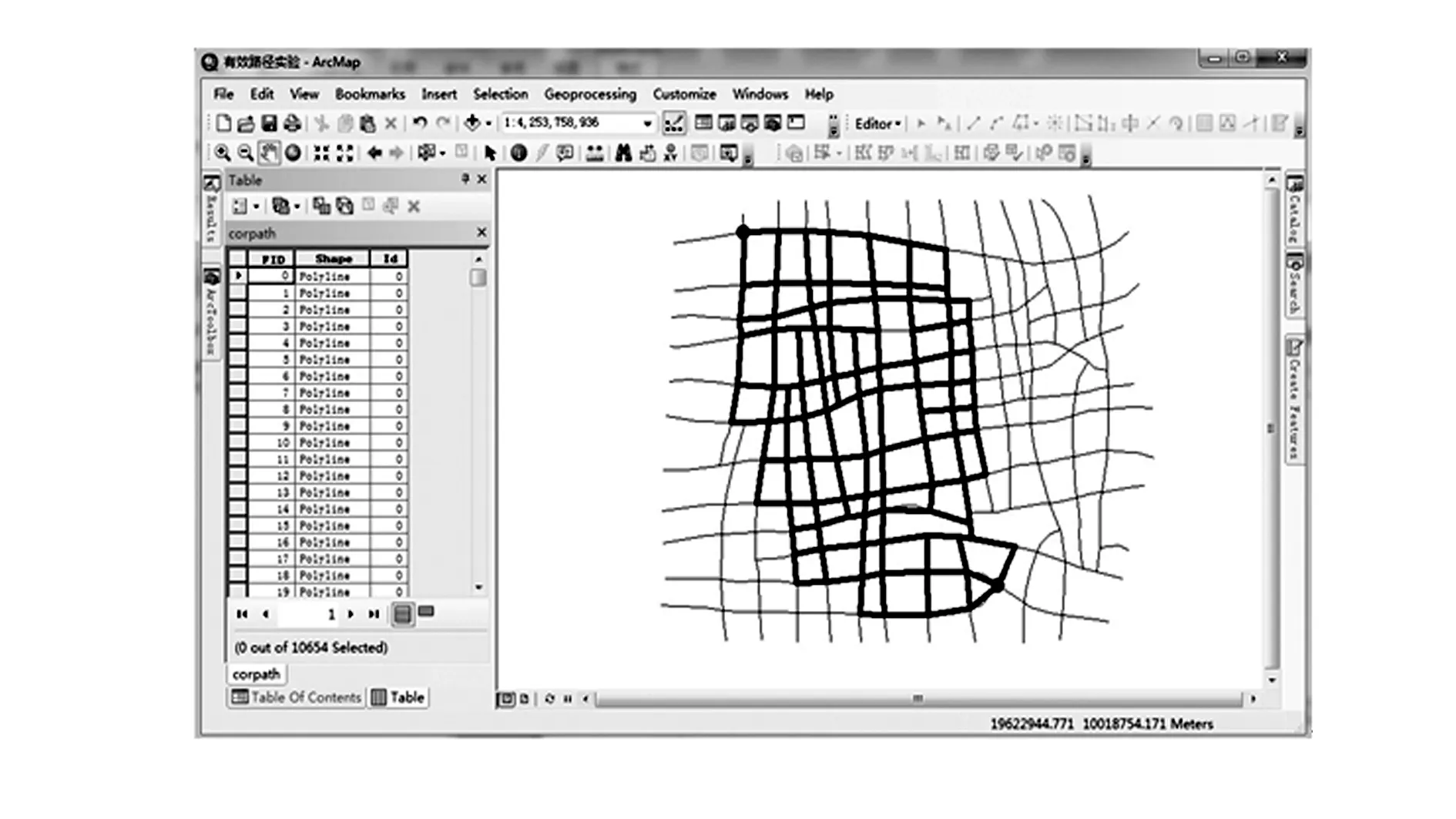

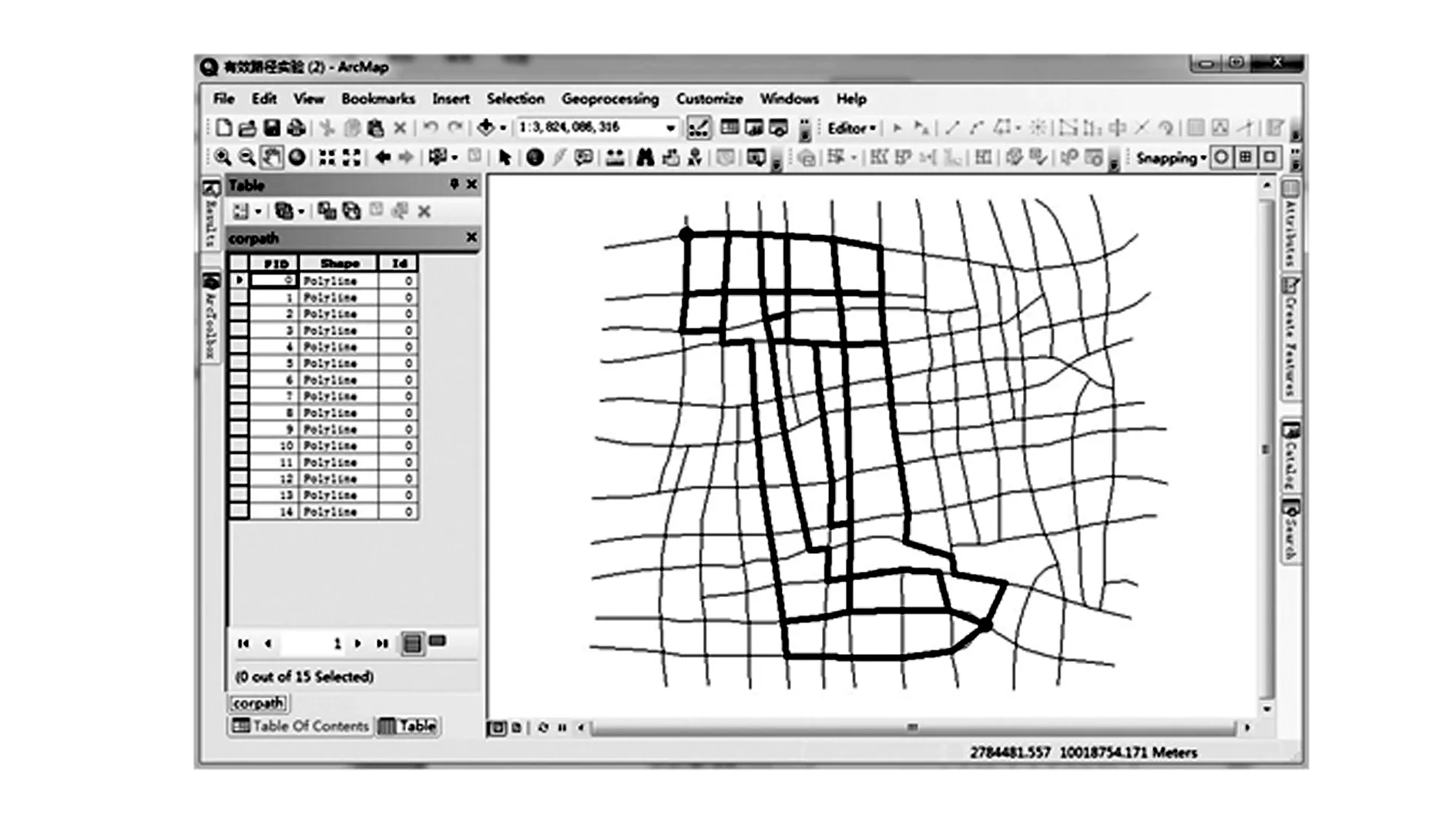
4 结 语
