发动机振动信号时频分析方法比较

吴春志，贾继德，姜斯平

(1.军事交通学院 军用车辆系，天津 300161； 2. 蚌埠汽车士官学校 基础部，安徽 蚌埠 233011)



发动机振动信号时频分析方法比较

吴春志1，贾继德1，姜斯平2

(1.军事交通学院 军用车辆系，天津 300161； 2. 蚌埠汽车士官学校 基础部，安徽 蚌埠 233011)

在发动机故障诊断、特征提取中时频分析是一种重要的方法。利用包含调频波和谐波的仿真信号对Gabor变换、小波变换、Wigner分布、平滑Wigner分布、Hilbert-Huang变换以及压缩小波等时频分析方法，在时间分辨率、频率分辨率以及多分量信号识别能力上进行了比较，并用发动机实测信号进行了分析验证。结果表明，压缩小波能提供较高的时频分辨率，而且对特征频段能够实现精细重构。

时频分析；特征提取；压缩小波

在发动机故障诊断领域，通常通过分析发动机振动信号提取故障特征信息。而探索故障信息提取途径以及发展新的故障诊断理论和技术，越来越依靠现代信号处理的理论方法和技术手段。

发动机振动信号具备多分量、非平稳等特性。对于这样的信号，时频分析是一种有效的分析方法。它可以将时间和频率的局部化，通过时间轴和频率轴两个坐标组成的平面得到整体信号在局部时域内的频率组成，或者看出整体信号各个频带在局部时间上的分布和排列情况。近年来，在发动机故障诊断中，许多时频分析方法都得到应用，如：Gabor变换[1]、连续小波变换(continuous wavelet transform, CWT)[2]、Hilbert-Huang变换(HHT)[3]等；二次型(魏格纳分布(Wigner-Ville distribution, WVD)[4]、平滑魏格纳分布(smoothing pseudo-Wigner-Ville distribution, SPWVD)[5])；压缩小波变换(synchrosqueezed wavelet transform, SWT)[6-8]等。孔庆鹏等[9]利用Gabor变换及时频域掩码滤波对振动信号进行阶比分析，能够提取指定的阶比系数;臧玉萍等[10]将故障信号进行离散小波变换，分解出近似系数和细节系数，自相关消噪后进行连续小波变换，在时频图中确定了故障类别;郑海波等[5]引入平滑伪魏格纳维尔分布，有效地提取异响故障特征信息，识别不同的发动机异响故障;夏天等[11]将EMD分解与AR谱技术结合，准确反映了柴油机曲轴轴承磨损的状态;刘景良等[12]将同步压缩小波应用到识别结构的瞬时频率上，取得了明显的效果。从大量文献给出的结果来看，每种时频分析方法都取得了一定的效果。然而，由于缺乏多种时频分析方法的综合比较，直接影响了时频分析方法在该领域的广泛应用。为此，本文以发动机振动信号分析为目的，对几种时频分析方法进行比较，为发动机振动信号处理选择合适的时频分析方法。

首先建立多分量、非平稳仿真模拟信号，应用Gabor变换、连续小波变换、魏格纳分布、平滑魏格纳分布、HHT变换以及压缩小波变换等时频分析方法进行分析对比，重点考核每种方法在时间分辨率、频率分辨率以及多分量信号识别能力，比较各个方法的优缺点。最后，利用其中性能较好的方法对发动机实测振动信号进行分析，进而提取故障特征，进行故障的诊断识别。

1　时频方法对比

1.1Gabor变换(STFT)

传统的傅里叶变换是适用于平稳信号的分析和处理方法，然而，发动机的振动信号是非平稳的，是随着时间而变化的。为了能够同时在时间—频率域描述振动信号的时频特性，通过对信号加窗，并假定窗内的信号是平稳的，在窗函数内进行傅里叶变换，来分析其间隔内信号的频率特征，从而形成了短时傅里叶变换。但是，不论窗函数如何选择都无法同时使时间和频率的分辨率达到最优。当窗函数选择为高斯窗时，可使时间和频率的分辨率乘积达到最小，Δt×Δω=1/2，此时的变换即为Gabor变换[4]。高斯窗函数h(t)表达式为

(1)

式中a控制高斯窗的长度，它决定着Gabor变换的时频分辨率。

1.2连续小波变换(CWT)

小波变换是一种新的变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间—频率”窗口，是进行信号时频分析和处理的理想工具。小波变换可以根据实际分析的需要，自适应地调节时频窗口，能够聚焦到信号时域和频域的任意细节，被誉为信号分析的“显微镜”[13]。

信号s(t)的连续小波变换定义为

(2)

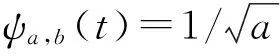
当母小波为Morlet小波时，

ψ0(t)=π-1/4eiω0te-t2/2

(3)

式中：t为时间；ω0为无量纲频率。

当ω0=6时，小波尺度a与傅里叶周期基本相等，尺度项与周期项可以相互替代，所以Morlet小波在时间与频率的局部化之间有着很好的平衡。

1.3魏格纳分布(WVD)

短时傅里叶变换和小波变换都属于线性时频分析的范围，因为测不准原理使得时间和频率分辨率无法同时达到最高。魏格纳分布是一种二次型的时频分析方法，能从时、频准确地描述信号本身[14]。

信号S(t)的Wigner-Ville分布定义为

(4)

式中ω为信号频率。

虽然Wigner-Ville分布具有很多优良的数学性质，但它却并不满足可加性。仿真信号S(t)=S1(t)+S2(t)，将它代入式(5)可知信号S1(t)的Wigner-Ville分布为

WVDS(t,ω)=WVDS1(t,ω)+WVDS2(t,ω)+

WVDS1S2(t,ω)+WVDS2S1(t,ω)

(5)

式中附加项WVDS1S2(t,ω)+WVDS2S1(t,ω)通常称为交叉项。

Wigner-Ville分布对信号的时频聚集性在该领域是很高的，但是由于附加交叉项的存在使得Wigner-Ville分布在分析多分量信号时难以发挥应有的作用。

1.4平滑伪魏格纳分布(SPWVD)

为了克服魏格纳分布的交叉项干扰，可以针对信号的魏格纳分布，通过在其时域与频域加窗的方法，抑制交叉项，即平滑伪魏格纳分布，定义为

WVDS(t-u,ω-v)dudv

(6)

式中：WVD(t,ω)为魏格纳分布得到的时频矩阵；φ(t,ω)为二维低通滤波：

φ(t,ω)=e-αt2-βω2α>0，β>0

(7)

式中α和β分别为控制函数φ(t,ω)在时间域和频率域的扩展，通过选择适当的平滑参数，在某种程度上压缩了多分量信号的交叉项[15]。

1.5Hilbert-Huang变换(HHT)

Hilbert-Huang变换是经验模式分解(EMD)和Hilbert时频谱的统称。它首先将信号采用EMD方法分解为若干固有模态函数ci(IMF)和一个残余分量之和：

(8)

然后，对每个IMF分量进行Hilbert变换得到瞬时频率和瞬时幅值，进而得到信号的完整时间—频率分布。

Si(t)=ci(t)

(9)

(10)

式中p为柯西主分量。

通过此变换，Si(t)和Yi(t)可以组成解析信号zi(t)，即

zi(t)=Si(t)+iYi(t)=aieiθi(t)

(11)

其中

θi(t)=arctan (Yi(t))/Si(t))

(12)

定义瞬时频率为

则原信号可以表示为

(13)

1.6压缩小波变换(SWT)

压缩小波算法以小波变换为基础，类似EMD，但是在时频域有更高的分辨率。

由于压缩小波建立在小波变换的基础上，对于单一信号S(t)=Acos(ωt)进行连续小波变换可得

(14)

式中：ξ为母小波主频；a为尺度因子；Ws(a,b)为小波系数。

如果ξ=ω0，则理论上其小波系数谱应该集中在尺度a=ω0/ω上。实际得到的小波系数谱总是在尺度方向扩散，聚焦效果不理想，从而使时频图变得模糊。虽然小波系数在尺度方向上存在扩散，但其相位保持不变[16]。因此，针对Ws(a,b)，计算其瞬时频率：

(15)

式中arg (·)为复小波系数的相位。

通过计算瞬时频率，就可以把小波系数从(b,a)投影到(b,ωs(a,b))，这就是压缩小波变换的基本思想。对于离散情况，尺度坐标和频率坐标都是离散值(Δak=ak-ak-1，Δω=ωl-ωl-1)。因此，压缩小波变换的公式可以表述为[13]

(Δak))

(16)

SWT是一种时频重排算法，但是与以往的重排算法不同，SWT在提高时频分辨率的同时，还可以重构。重构信号s(t)可表述为

(17)

其中

2　仿真信号分析

2.1仿真信号建立

由于发动机振动的非平稳性，信号中往往包含多个调幅调频以及频率恒定的周期分量，为此建立仿真信号S模仿发动机信号进行分析。其中，仿真信号S=S1+S2+S3，S1是一个调频信号，中央频率为250 Hz，S2和S3是频率分别为60 Hz和70 Hz的谐波信号，即

S1=sin (2π×(250×t+3×sin 30×t))

S2=cos (2π×60×t)

(18)

S3=cos (2π×70×t)

采样频率为1 000 Hz，采样点数为1 024点，由此可得仿真信号的时域及频域谱(如图1所示)。

图1　仿真信号的时域及频域谱

2.2对比分析

由于Gabor变换(图2(a))窗函数固定，在分析60 Hz和70 Hz的周期信号时，时频聚集性较高，但是由于窗函数固定，导致250 Hz的调频信号的时频图像十分发散，分辨率较低，对频率相近的两个周期信号有一定程度的混叠。

图2　各方法所得的时频图

相较于Gabor变换，Morlet小波变换(图2(b))能够根据信号改变窗函数的大小，对于各个频率分量的信号都能在时频平面上有较为清晰地表达，尤其能够清晰分辨60 Hz和70 Hz的周期信号不存在混叠现象，但是时频聚集性不高。

Wigner分布(图2(c))对仿真信号中的调频和周期分量都表现出了极高的时频分辨率，但是两个分量之间有明显的交叉项干扰，而平滑Wigner分布(图2(d))较好地克服了中间的交叉项但是分辨率大大降低，而且对于两个频率相近的周期信号有着较强的混叠现象。

对多分量信号滤波进而分析单分量信号一直是一个难题，由图2(e) 所示，中心频率250 Hz的调频信号对应EMD筛选出的前两个IMF分量，虽然囊括了全部的信号特征，但是对于两个频率相近的谐波分量，EMD也没有很好地将二者区分开。

压缩小波可以提供高于Wigner分布的时频分辨率而且没有交叉项的干扰(图2(f))，对于调频波和谐波的高频和低频信号均能实现较高的分辨率，可以有效提取故障特征并且重构信号，是一种理想的处理发动机故障信号的时频分析手段。

3　实例信号分析

为了进一步验证压缩小波变换对实际信号分析能力，在东风EQ6100型发动机机油口测得连杆轴承噪声信号，采样频率4 000 Hz，取信号长度1 024。用上述几种方法对实测信号进行分析。

采用噪声计权网络中的A计权网络进行测试。因为它比较接近人耳对不同频率的响应，如人耳对低频不敏感，A声级计在低频处的衰减就很大[17]。采得的实测信号的时域图及频域图如图3所示。图4为重构信号的时域图及频域图。压缩小波变换模糊地提取出了信号的频率脊线(如图5所示)，而且对于信号超过1 000 Hz我们所不关心的部分能够较好地研磨，有利于提取信号的故障特征，对感兴趣的特征频段能够实现精细重构。

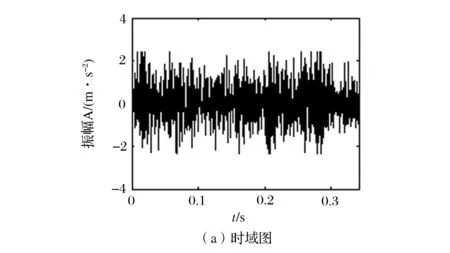
图3　实测信号时域及频域图

4　结　语

在发动机故障诊断领域，对采集到的信号进行特征提取，时频分析一直是一个非常重要的方法。本文利用仿真信号对短时傅里叶变换、Gabor变换、小波变换、Wigner分布、平滑Wigner分布、HHT变换、以及压缩小波等时频分析方法进行了比较，并用发动机连杆轴承的实测信号进行了验证。仿真和实测信号表明对于发动机故障信号压缩小波算法有较好的时频分辨率，没有窗函数选取以及交叉项的干扰，是一种优秀的时频分析方法。

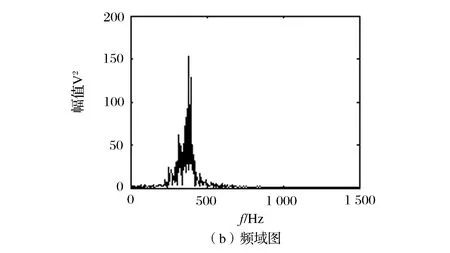
图4　重构信号的时域及频域图

图5　压缩小波对实测信号及重构信号的时频图

[1]沈虹,赵红东,张玲玲,等. 基于EMD和Gabor变换的发动机曲轴轴承故障特征提取[J]. 汽车工程,2014(12):1546-1550.

[2]ALHUSSEIN ALBARBAR.An investigation into diesel engine air-borne acoustics using continuous wavelet transform[J].Journal of Mechanical Science and Technology,2013,27(9):2599-2604.

[3]WANG Y S , MA Q H, ZHU Q, et al.An intelligent approach for engine fault diagnosis based on Hilbert-Huang transform and support vector machine[J].Applied Acoustics,2014,75(1):1-9.

[4]WU J D, HUANG C K .An engine fault diagnosis system using intake manifold pressure signal and Wigner-Ville distribution technique[J].Expert Systems with Application,2011,38(1):536-544.

[5]郑海波,李志远,陈心昭,等.基于时频分布的发动机异响特征分析及故障诊断研究[J].内燃机学报,2002,20(3):267-272.DOI:10.3321/j.issn:1000-0909.2002.03.016.

[6] WANG Z C , REN W X , LIU J L , et al. A synchrosqueezed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J]. Journal of Sound and Vibration,2013(332)：6016-6028.

[7]胡异丁,任伟新,杨栋,等.基于同步压缩变换和局部替代数据的非平稳振动信号分解方法[J].振动与冲击,2013,32(23):43-47.DOI:10.3969/j.issn.1000-3835.2013.23.008.

[8]陈小旺,冯志鹏,LIANG Ming,等.基于迭代广义同步压缩变换的时变工况行星齿轮箱故障诊断[J].机械工程学报,2015,(1):131-137.DOI:10.3901/JME.2015.01.131.

[9]孔庆鹏,宋开臣,陈鹰,等.发动机变速阶段振动信号时频分析阶比跟踪研究[J].振动工程学报,2005,18(4):448-452.DOI:10.3969/j.issn.1004-4523.2005.04.010.

[10]臧玉萍,张德江,王维正,等.基于小波变换技术的发动机异响故障诊断[J].机械工程学报,2009,45(6): 239-245.DOI:10.3901/JME.2009.06.239.

[11]夏天,王新晴,肖云魁,等.应用EMD-AR谱提取柴油机曲轴轴承故障特征[J].振动、测试与诊断,2010,30(3):318-321.DOI:10.3969/j.issn.1004-6801.2010.03.023.

[12]刘景良,任伟新,王佐才等.基于同步挤压小波变换的结构瞬时频率识别[J].振动与冲击,2013,32(18):37-42,48.DOI:10.3969/j.issn.1000-3835.2013.18.007.

[13]尚帅,韩立国,胡玮,等. 压缩小波变换地震谱分解方法应用研究[J]. 石油物探,2015(1):51-55，82.

[14]刘涛,曾祥利，曾军.实用小波分析入门[M].北京：国防工业出版社，2006：53.

[15]乔龙，赵慧敏，任金成,等.基于阶比跟踪和平滑伪Wigner-Ville分布的曲轴轴承机械故障特征提取[J].军事交通学院学报,2013,15(1):52-57.

[16]DAUBECHIES I, MAES S. A nonlinear squeezing of the continuous wavelet transform based onauditory nerve models[J]. Wavelets in Medicine and Biology, 1996: 527-546.

[17]贾继德,孔凡让,刘永斌,等.发动机连杆轴承故障噪声诊断研究[J].农业机械学报,2005,36(6): 87-91.DOI:10.3969/j.issn.1000-1298.2005.06.024.

(编辑：关立哲)

Comparison of Engine Vibration Signal Time-Frequency Analyzing Methods

WU Chunzhi1, JIA Jide1, JIANG Siping2

(1. Military Vehicle Department, Military Transportation University, Tianjin, 300161, China; 2. General Courses Department, Bengbu Automobile NCO Academy, Bengbu 233011, China)

Time-frequency analysis is widely used in engine fault diagnosis and feature extraction. In this paper, the simulated signals with FM and harmonic wave are used to compare the time-frequency analyzing methods in their capability of identifying time resolution, frequency resolution and the multi-component signals. The methods compared are: short time fourier transform (STFT), gabor transform, continuous wavelet transform (CWT), Wigner-Ville distribution (WVD), smoothing pseudo-Wigner-Ville distribution (SPWVD), Hilbert-Huang transform and synchrosqueezed wavelet transform(SWT). The the result of the comparison is verified with the real signals of the engine, which shows that SWT is capable not only of providing high time-frequency respresentation but also of refining the reconstruction of frequency band.

time-frequency analysis; feature extraction; synchrosqueezed wavelet

2015- 12-23；

2016-01-17.

总后勤部重点项目(BS311C011).

吴春志(1991—)，男，硕士研究生；

贾继德(1962—)，男，教授，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2016.04.009

TK421.6

A

1674-2192(2016)04- 0035- 06