创意平板折叠桌数学模型的设计与研究

李婉婷

（吉林师范大学，吉林四平136000）

创意平板折叠桌数学模型的设计与研究

李婉婷

（吉林师范大学，吉林四平136000）

对平板折叠桌的设计原理及优化可能性进行一系列的数据挖掘与分析，确立创意平板折叠桌的设计方案。利用空间曲线的参数方程、超静定次数、力矩平衡、抗弯强度、坐标拟合为理论基础研究，最终确定折叠桌最优设计加工参数，进行点与曲线的坐标拟合，并利用matlab描点绘制动态变化过程图。

超静定次数；力矩平衡；抗弯强度；坐标拟合

现如今，折叠与伸展已成为家具行业的基本设计理念。折叠桌以其节省空间的特点深受消费者喜爱。本文设计的创意平板折叠桌是一种新型开发的可折叠桌子，它的设计灵感源自错综复杂的自然形式，桌面呈圆形，桌腿能够随着铰链的活动，平摊成一张平板。桌腿由若干根木条组成，分成两组，每组各用一根钢筋将木条连接，钢筋两端分别固定在桌腿各组最外侧的两根木条上，并且木条留有空槽以保证滑动的自由度，桌子外形由直纹曲面构成。

1　模型建立的条件

为了使问题更加清晰，对建模问题进行以下假设：木板长度减去两条最长桌腿长度为最小边缘预留长度，假设最小边缘等于每根木条的宽度；所有折叠后桌子的高度都包括木板本身的高度；假设桌面均匀受力，中心木条到最外侧桌脚木条的角度变化量是一个恒定值。

2　模型的建立与求解

2.1确定桌腿长度和未折叠前钢筋初始位置

通过查阅相关资料和视频，为了保证桌腿各个木条在折叠过程中摩擦的自由度，本文考虑到桌腿每个木条之间存在缝隙，当已知长方形木板尺寸为120 cm×50 cm×30 cm，每根木条宽2.5 cm时，一组桌腿木条数为19根，建立平面直角坐标系，如图1所示。

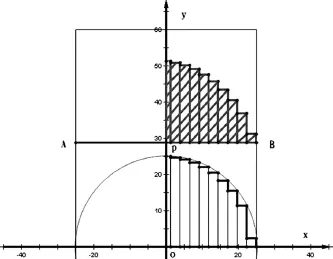
图1　折叠桌一侧的平面直角坐标系

b、c已知，故可得半径r的长度为：

木板由19根木条组成，木板宽50 cm，每根木条宽2.5 cm，则各个木条之间必存在缝隙，缝隙d为：

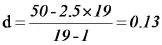
所以从中间木棍的下一根木棍开始每条木棍的横坐标都在前一坐标的基础上加2.5+d= 2.63cm，即

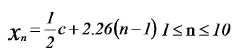
在已知Xn的提前下，应用圆的标准方程可以得到对应的Yn的值：

2.2桌腿木条的开槽

桌腿完全折叠后，桌子的高线长度与最长桌腿长度已知，且夹角固定，可得出平面示意图，如图2所示。

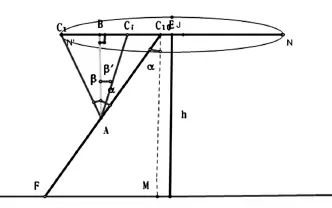
图2　桌子完全折叠后平面示意图

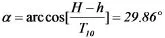
因为三角形C10MF与三角形ABC10相似，线段AB为高H-h的一半，因此可知线段BC10的长度：

在三角形ABC1中应用勾股定理可得桌子上每条腿从桌面边缘到钢筋位置的距离：

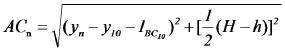
结合图1，用求得当桌子打开后钢筋所在位置，钢筋处于在最长桌腿中部，可知钢筋在图1上的坐标是Y=28.83，那么开槽长度为：

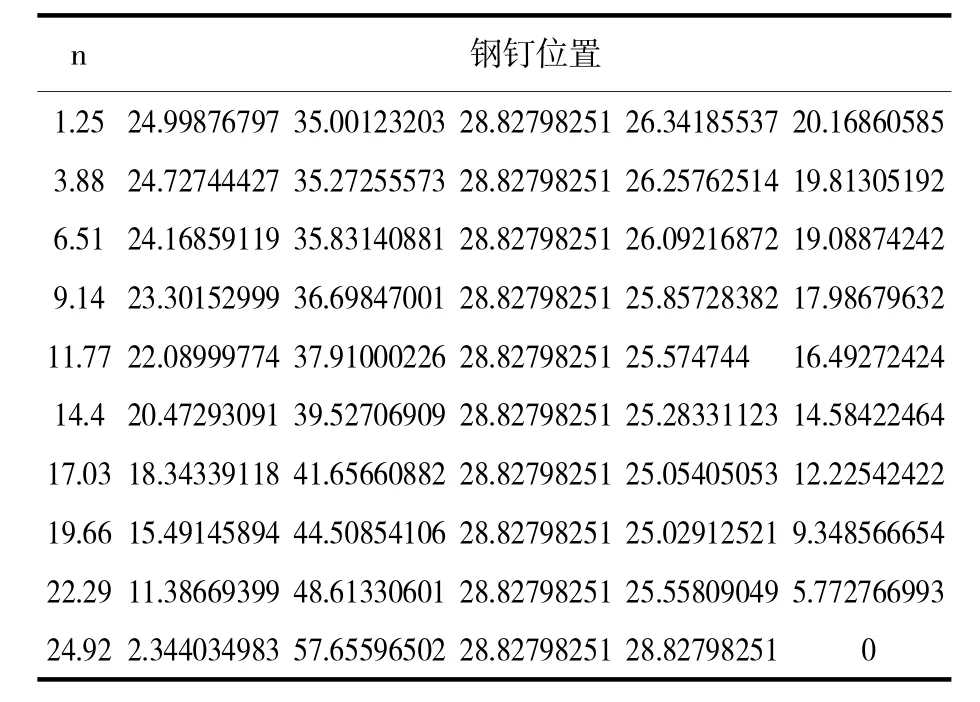
表1　各桌腿木条开槽长度表

2.3桌角边缘线

针对平板右半部分，桌面固定，桌腿向上抬起，建立空间直角坐标系，如图3所示。

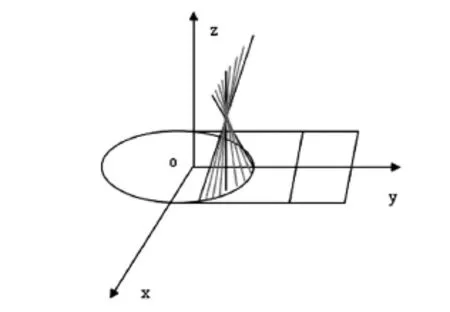
图3　桌子右半部分空间直角坐标系

当平板折叠成桌子后，每条桌腿与x-y平面形成角，由图3可知折起后桌腿的x轴坐标未变，而y轴坐标变为：，z轴坐标变为：。

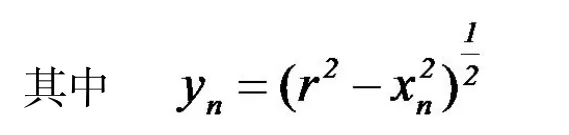
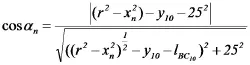
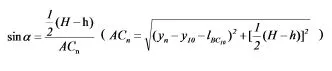
2.4对桌子进行力学分析

首先对于桌子的力学性能进行分析，我们将桌子除支撑外的所有木条以及对应的钢筋都去掉，得到结构及其力学模型（图中另一侧的两个台脚没有画出，实际存在），如图4所示。

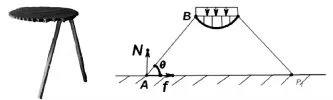
图4　仅有支撑木条的结构及其力学模型

右图是对应简支梁的弯矩图，若f即摩擦力不足够大，会导致结构发生变化。当增加桌腿木条数和钢筋，结构发生变化。如图5所示。

图5　增加木条和钢筋后的结构

根据力学原理，每增加一根木条，该结构的超静定次数便多增加一次，因此该结构为多次超静定结构，采取增加木条的方法来增加超静定次数，降低受力敏感度，是提高其稳定性的重要因素。多年的工程实践证明，采用优良的结构形式，对抵抗较大幅度的超载、随机外力以及避免脆性破坏或连续破坏有十分重要的意义。

2.5确定最优角度

为了尽可能减少摩擦力对整个结构受力的影响，桌脚木条与水平面的夹角应该有所限制若杆AB的长度为L，f为摩擦力，N为支持力根据力矩平衡，对B点求矩：

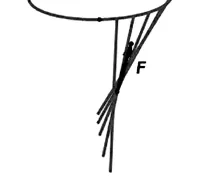
图6　支撑桌腿与水平面垂直时示意图

根据受力平衡，对于桌脚木条来说就会受到钢筋提供的很大的向外侧的力作用，对于力学性能来说是一个很大的影响。因此对于整体结构来说，桌脚与水平面的夹角为90°并不是最佳角度。

由于通过增加木条数去提高木板桌的稳定性，所以在木条数量较多的前提下，假设中心木条到最外侧桌脚木条的角度变化量是一个恒定值，即它们与水平面的夹角是一个等差数列。

最外侧桌脚木条与水平面所成角是定值，根据上一问求出的最长的桌腿与折叠后桌子高线的夹角为29.86°，可知最外侧桌脚木条与水平面的夹角60.14°，以及中间木条与水平面的夹角71.62°，可以求得最佳角度。

2.6制作星形桌面桌

根据用户给定的已知条件：折叠桌高度、桌面边缘线形状以及桌脚边缘线形状，之后通过合理的数学模型，能够得到成品桌的大致模型，和相关必备参数（平板尺寸、槽口长度等），制订相应的制作方法。

利用matlab进行动态分析问题，通过分析得到高度、桌面边缘线、桌脚边缘线之间的关系并不割裂，三者之间相互影响，不可分割。在考虑实用性、稳定性等其他一系列必要条件后，将得到折叠桌制作参数的一个大致范围，制作折叠桌的大致动态模式图。

3　模型的评价与讨论

3.1模型缺点

由于在计算圆形半径时，假定了桌面两边的最短木条长度与木条宽度一致，因此最后的数值会有偏差。不能灵活地根据客户任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状准确绘制出桌子变化过程，使生产的折叠桌尽可能接近所期望的形状。

3.2模型优点

此模型针对稳固程度、加工方便与否、用料多少进行了优化，找到了对于任意给定的折叠桌高度和圆形桌面直径后，求得最优设计加工参数的简便方法。由matlab所建立的数学模型，可以满足顾客任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状。绘制出的折叠桌尽可能接近客户所期望的形状，节省了大量的工作时间。

［1］蒋玉川，徐双武，胡耀华，等.结构力学［M］.沈阳：科学出版社，2012.

［2］王新敏.Ansys结构动力分析与应用［M］.北京：人民交通出版社，2014.

［3］丁星，王清远.MATLAB杆系结构分析［M］.沈阳：科学出版社，2008.

［4］赵经文，王宏钰.结构有限元分析［M］.沈阳：科学出版社，2001.

［责任编辑：秦锦文］

The Design and Research of Creative Flat Folding Table Mathematical Model

LI Wanting
(Jilin Normal University,Siping 136000,China)

A series of data mining and analysis of the flat folding table design principle and optimization possibility are done,and the design scheme of the flat folding table is established.The researcher takes the parameter equation of space curve,the degree of statical indeterminacy,torque balance,flexural strength, coordinate fitting as the theoretical basis of the research,finally determines the optimum design and processing parameters of the flat folding table,fits the coordinate of points and curves,and draws the dynamic change process picture by matlab tracing point.

degree of statical indeterminacy;torque balance;flexural strength;coordinate fitting

O22

A

2095-5928（2016）04-32-04

10.16850/j.cnki.21-1590/g4.2016.04.010

2016-03-11

2014高教社杯全国大学生数学建模竞赛项目

李婉婷（1992-），女，辽宁黑山人，硕士，研究方向：运筹学与控制论。